洛谷P1162 - 填涂颜色
题目描述
由数字 0 0 0 组成的方阵中,有一任意形状闭合圈,闭合圈由数字 1 1 1 构成,围圈时只走上下左右 4 4 4 个方向。现要求把闭合圈内的所有空间都填写成 2 2 2。例如: 6 × 6 6\times 6 6×6 的方阵( n = 6 n=6 n=6),涂色前和涂色后的方阵如下:
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
输入格式
每组测试数据第一行一个整数 n ( 1 ≤ n ≤ 30 ) n(1 \le n \le 30) n(1≤n≤30)。
接下来 n n n 行,由 0 0 0 和 1 1 1 组成的 n × n n \times n n×n 的方阵。
方阵内只有一个闭合圈,圈内至少有一个 0 0 0。
输出格式
已经填好数字 2 2 2 的完整方阵。
样例 #1
样例输入 #1
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
样例输出 #1
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
提示
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 30 1 \le n \le 30 1≤n≤30。
一、错误分析
题意就是把被1包围的0改成2。
那么只需要找到包围起来的第一个0的坐标,就可以把所有被包围的0改成2。
第一个0的坐标是第一个1的右下角?
那么就有了下面错误的代码,WA了一个测试点
//错误代码
#include <iostream>
#include <queue>
using namespace std;
int n;
int dir[][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int a[33][33];
struct node
{int x, y;
};
int main()
{cin >> n;int sx = 0, sy = 0;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++){cin >> a[i][j];if (a[i][j] == 1 && sx == 0){sx = i, sy = j;}}sx++;sy++;// bfs广度优先queue<node> q;q.push({sx, sy});while (!q.empty()){node p = q.front();q.pop();for (int i = 0; i < 4; i++){int nx = p.x + dir[i][0], ny = p.y + dir[i][1];if (!(nx>n||ny>n||nx<1||ny<1)&&a[nx][ny] == 0){q.push({nx, ny});a[nx][ny] = 2;}}}for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){cout << a[i][j] << " ";}cout << endl;}
}
那么当墙有厚度的时候,这种找0的方法是错误的。
比如下面这组测试数据。
6
1 1 1 1 1 1
1 0 0 0 0 0
1 1 1 1 1 1
1 1 0 0 1 1
1 1 0 0 1 1
1 1 1 1 1 1
二、正确分析
先将二维数组初始化为2,将有1的地方改为1,那么被1包围之外的2就是连续的了,只需要使用dfs或bfs就能够把所有包围之外的2改为0。
二维数组需要往外扩展一圈,这样就能保证包围之外的2是连续的。
如[1,n]的区间拓展为[0,n+1].
方法1.DFS
#include <iostream>
#include <queue>
using namespace std;
int n;
int dir[][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int a[35][35];
struct node
{int x, y;
};
void dfs(int x,int y)
{if(x>n+1||y>n+1||x<0||y<0) return ;if(a[x][y] == 1||a[x][y]==0) return;a[x][y]=0;for (int i = 0; i < 4; i++){dfs(x + dir[i][0],y + dir[i][1]);}
}
int main()
{for(int i=0;i<33;i++)for(int j=0;j<33;j++){a[i][j]=2;}cin >> n;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++){int t;cin >> t;if(t==1) a[i][j]=1;}dfs(0,0);for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){cout << a[i][j] << " ";}cout << endl;}
}
方法2.BFS
#include <iostream>
#include <queue>
using namespace std;
int n;
int dir[][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int a[35][35];
struct node
{int x, y;
};
int main()
{for(int i=0;i<33;i++)for(int j=0;j<33;j++){a[i][j]=2;}cin >> n;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++){int t;cin >> t;if(t==1) a[i][j]=1;}queue<node> q;q.push({0, 0});while (!q.empty()){node p = q.front();q.pop();for (int i = 0; i < 4; i++){int nx = p.x + dir[i][0], ny = p.y + dir[i][1];if (!(nx>n+1||ny>n+1||nx<0||ny<0)&&a[nx][ny] == 2){q.push({nx, ny});a[nx][ny] = 0;}}}for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){cout << a[i][j] << " ";}cout << endl;}
}
相关文章:

洛谷P1162 - 填涂颜色
题目描述 由数字 0 0 0 组成的方阵中,有一任意形状闭合圈,闭合圈由数字 1 1 1 构成,围圈时只走上下左右 4 4 4 个方向。现要求把闭合圈内的所有空间都填写成 2 2 2。例如: 6 6 6\times 6 66 的方阵( n 6 n6 n6&…...
)
设计模式十一:外观模式(Facade Pattern)
外观模式(Facade Pattern)是一种结构型设计模式,它提供了一个统一的接口,用于访问系统中的一组复杂子系统。外观模式通过将复杂子系统的接口封装在一个高层接口中,简化了客户端与子系统之间的交互,使得客户…...
GIS和倾斜摄影的关系?
GIS(地理信息系统)和倾斜摄影是两种在地理空间数据处理和分析中扮演重要角色的技术。但是我们总是会分不清二者,本文就带大家从不同角度了解二者之间的关系。 概念 GIS是一种用来捕获、存储、分析和展示地理空间数据的技术,它可以…...

【CI/CD】图解六种分支管理模型
图解六种分支管理模型 任何一家公司乃至于一个小组织,只要有写代码的地方,就有代码版本管理的主场,初入职场,总会遇到第一个拦路虎 git 管理流程,但是每一个企业似乎都有自己的 git 管理流程,倘若我们能掌握…...
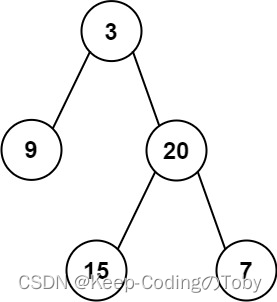
LeetCode105. 从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树 文章目录 [105. 从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)一、题目二、题解 一、题目 给定两个整数数组 preorder 和 inorder ,其中 preo…...
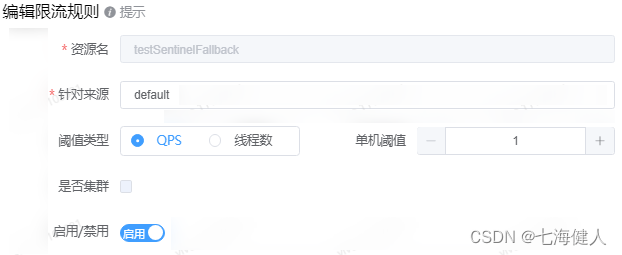
编码技巧——Sentinel的blockHandler与fallback
本文介绍Sentinel的blockHandler与fallback的区别,背景是:发生限流时,配置的sentinel的blockhandler没有生效而fallback生效了;排查原因,从而给出Sentinel配置异常降级和限流降级的代码写法; 在查看源码前…...

最新成果展示:GaN基Micro-LED热学模型数据库的开发及应用
由于GaN基Micro-LED表面积-体积比增加,其在热学方面的性质有别于大尺寸的LED,如缺陷复合导致的热效应将在发光区域中产生诸多“热”点,导致发光波长不均匀,这将影响后期显示系统的成像稳定性。针对上述问题,天津赛米卡…...

【Vue3】动态组件
动态组件的基本使用 动态组件(Dynamic Components)是一种在 Vue 中根据条件或用户输入来动态渲染不同组件的技术。 在 Vue 中使用动态组件,可以使用 元素,并通过 is 特性绑定一个组件的名称或组件对象。通过在父组件中改变 is 特…...

Java超级玛丽小游戏制作过程讲解 第五天 创建并完成常量类04
//加载障碍物 try {obstacle.add(ImageIO.read(new File(path"brick.png")));obstacle.add(ImageIO.read(new File(path"soil_up.png")));obstacle.add(ImageIO.read(new File(path"soil_base.png"))); } catch (IOException e) {e.printStackTr…...

设置浏览器兼容
浏览器兼容 css兼容 cursor定义手型 Firefox不支持hand,IE支持pointer 解决方法:统一使用pointercss透明 IE:filter:progid:DXImageTransform.Microsoft.Alpha(style0,opacity60) Firefox:opacity:0.6 解决…...

Java # List
ArrayList<>() import java.util.ArrayList; // 引入 ArrayList 类ArrayList<E> objectName new ArrayList<>(); // 初始化 常用方法 方法描述add()将元素插入到指定位置的 arraylist 中addAll()添加集合中的所有元素到 arraylist 中clear()删除 arrayl…...

git原理与使用
目录 引入基本操作分支管理远程操作标签管理 引入 假设你的老板要你设计一个文档,当你设计好了,拿给他看时,他并不是很满意,就要你拿回去修改,你修改完后,再给他看时,他还是不满意,…...
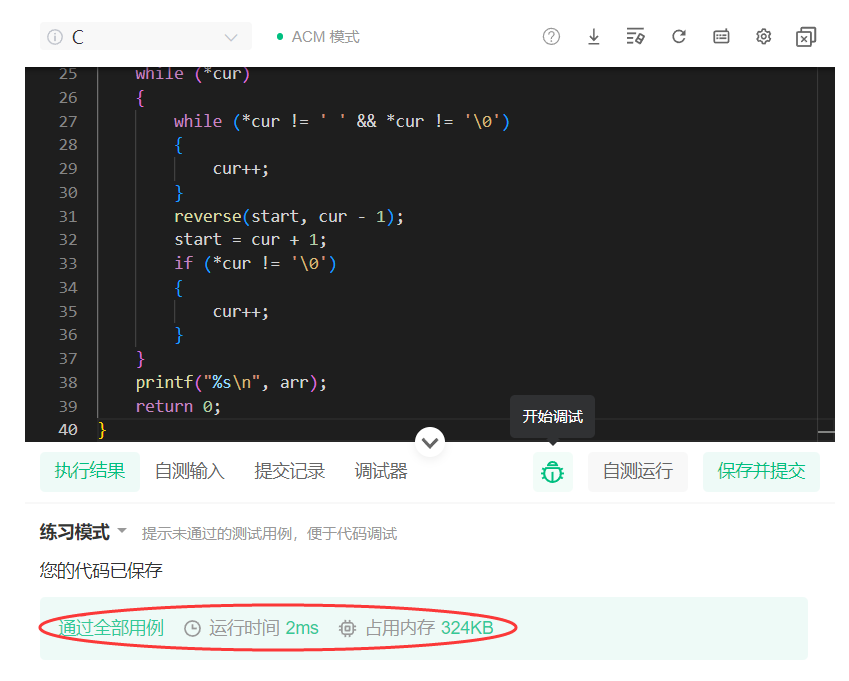
【C语言题解】将一句话的单词进行倒置,标点不倒置。
题目描述:将一句话的单词进行倒置,标点不倒置。比如 “I like beijing.”,经过处理后变为:“beijing. like I”。 文章目录 原题目题目描述:输入描述:输出描述:题目链接: 整体思路分…...
Postman 的简单使用
什么是Postman 在程序开发中用于调试网络程序或者跟踪网页请求。可以对网页进行简单的基本信息调试。Postman最早是作用chrome浏览器插件存在的,但是2018年初Chrome停止对Chrome应用程序的支持。所以现在Postman提供了独立的安装包,不再依赖于Chrome浏览…...

在CentOS7安装部署GitLab服务
CentOS 7 安装 Gitlab 官方安装教程:https://about.gitlab.com/install/ 参考安装教程:https://developer.aliyun.com/article/74395 安装配置 Step1:配置yum源 vim /etc/yum.repos.d/gitlab-ce.repo存入以下内容: [gitlab-c…...
订单系统就该这么设计,稳的一批~
订单功能作为电商系统的核心功能,由于它同时涉及到前台商城和后台管理系统,它的设计可谓是非常重要的。就算不是电商系统中,只要是涉及到需要交易的项目,订单功能都具有很好的参考价值,说它是通用业务功能也不为过。今…...

Agents改变游戏规则,亚马逊云科技生成式AI让基础模型加速工作流
最近,Stability AI正式发布了下一代文生图模型——Stable Diffusion XL 1.0这次的1.0版本是Stability AI的旗舰版生图模型,也是最先进的开源生图模型。 在目前的开放式图像模型中,SDXL 1.0是参数数量最多的。官方表示,这次采用的…...
详细教程:如何搭建废品回收小程序
废品回收是一项环保举措,通过回收和再利用废弃物品,可以减少资源浪费和环境污染。近年来,随着智能手机的普及,小程序成为了推广和运营的重要工具。本文将详细介绍如何搭建一个废品回收小程序。 1. 进入乔拓云网后台 首先…...

什么是双亲委派机制?
什么是双亲委派机制? Parent Delegation Model ,直译过来可能叫做父级委托模型更容易理解 类的加载过程 Java 编译器将 Java源文件编译成.class 文件再由 JVM 加载 .class 文件到内存中JVM 装载完成后得到一个 Class 字节码对象拿到字节码对象之后 &a…...

Mageia 9 RC1 正式发布,Mandriva Linux 发行版的社区分支
导读Mageia 9 首个 RC 已发布。公告写道,自 2023 年 5 月发布 beta 2 以来,Mageia 团队一直致力于解决许多顽固问题并提供安全修复和新特性。 新版本的控制中心添加了用于删除旧内核的新功能,该功能在 Mageia 9 中默认自动启用,用…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
