最优化:建模、算法与理论
最优化:建模、算法与理论
目前在学习 最优化:建模、算法与理论这本书,来此记录一下,顺便做一些笔记,在其中我也会加一些自己的理解,尽量写的不会那么的条条框框(当然最基础的还是要有)
第二章 基础知识
2.1 范数
2.1.1 向量范数
定义2.1(范数)称一个从向量空间Rn到实数域R的非负函数||·||为范数,如果他满足:
(1)正定性:对于所有的 v ∈ R n v{\in}R^n v∈Rn,有 ∣ ∣ v ∣ ∣ > = 0 ||v|| >= 0 ∣∣v∣∣>=0,且 ∣ ∣ v ∣ ∣ = 0 ||v|| = 0 ∣∣v∣∣=0 当且仅当 v = 0 v=0 v=0
(2)齐次性:对于所有的 v ∈ R n v{\in}R^n v∈Rn和 α ∈ R {\alpha}{\in}R α∈R,有 ∣ ∣ α v ∣ ∣ ||{\alpha}v|| ∣∣αv∣∣= ∣ α ∣ |{\alpha}| ∣α∣ ∣ ∣ v ∣ ∣ ||v|| ∣∣v∣∣
(3)三角不等式:对于所有的 v , w ∈ R n v,w{\in}R^n v,w∈Rn,有 ∣ ∣ v + w ∣ ∣ < = ∣ ∣ v ∣ ∣ + ∣ ∣ w ∣ ∣ ||v+w|| <= ||v|| + ||w|| ∣∣v+w∣∣<=∣∣v∣∣+∣∣w∣∣
最常用的向量范数为lp范数(p >= 1)
∣ ∣ v ∣ ∣ p = ( ∣ v 1 ∣ p + ∣ v 2 ∣ p + … + ∣ v n ∣ p ) 1 / p ||v||_{p} = (|v_{1}|^p + |v_{2}|^p + \ldots + |v_{n}|^p)^{1/p} ∣∣v∣∣p=(∣v1∣p+∣v2∣p+…+∣vn∣p)1/p
显而易见,高数应该都学过,如果 p = ∞ p={\infty} p=∞,那么 l ∞ l_\infty l∞范数定义为 ∣ ∣ v ∣ ∣ ∞ = m a x ∣ v i ∣ ||v||_\infty = max|v_i| ∣∣v∣∣∞=max∣vi∣
记住 p = 1 , 2 , ∞ p = 1,2,{\infty} p=1,2,∞的时候最重要,有时候我们会忽略 l 2 l_2 l2范数的角标
也会遇到由正定矩阵 A A A诱导的范数,即 ∣ ∣ x ∣ ∣ A = x T A x ||x||_A = \sqrt{x^TAx} ∣∣x∣∣A=xTAx
对于 l 2 l_2 l2范数,有常用的柯西不等式,设 a , b ∈ R n a,b{\in}R^n a,b∈Rn,则
∣ a T b ∣ < = ∣ ∣ a ∣ ∣ 2 ∣ ∣ b ∣ ∣ 2 |a^Tb|<=||a||_2||b||_2 ∣aTb∣<=∣∣a∣∣2∣∣b∣∣2
等号成立当且仅当a与b线性相关
2.1.2 矩阵范数
矩阵范数首先也一样要满足那三个特性啦,就是要满足正定性,齐次性,三角不等式,常用的就是 l 1 , l 2 l_1,l_2 l1,l2范数,当 p = 1 p = 1 p=1时,矩阵 A ∈ R m ∗ n A{\in}R^{m*n} A∈Rm∗n的范数定义
∣ ∣ A ∣ ∣ 1 = ∑ i = 1 m ∑ j = 1 n ∣ a i j ∣ ||A||_1={\sum_{i=1}^m}{\sum_{j=1}^n}|a_{ij}| ∣∣A∣∣1=i=1∑mj=1∑n∣aij∣
当 p = 2 p=2 p=2时,也叫矩阵的Frobenius范数(F范数),记为 ∣ ∣ A ∣ ∣ F ||A||_F ∣∣A∣∣F,其实就是所有元素的平方和然后开根号,具体定义如下
∣ ∣ A ∣ ∣ F = T r ( A A T ) = ∑ i , j a i j 2 ||A||_F=\sqrt{Tr(AA^T)}=\sqrt{\sum_{i,j}a_{ij}^2} ∣∣A∣∣F=Tr(AAT)=i,j∑aij2
这里的 T r Tr Tr表示方阵X的迹(这个大家应该都知道吧,我把百度的解释搬过来—在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)),矩阵的F范数具有正交不变性。
正交不变性呢就是说对于正交矩阵 U ∈ R m ∗ n , V ∈ R m ∗ n U{\in}R^{m*n},V{\in}R^{m*n} U∈Rm∗n,V∈Rm∗n,我们有
∣ ∣ U A F ∣ ∣ F 2 = ∣ ∣ A ∣ ∣ F 2 ||UAF||_F^2=||A||_F^2 ∣∣UAF∣∣F2=∣∣A∣∣F2
具体的推导我这里就不写了哈,打公式太麻烦了哈哈,感兴趣的可以看这本书的第24页或者来找我^^
矩阵范数也可以由向量范数给诱导出来,一般称这种算数为诱导范数,感觉用的不是很多,这里先不扩展开了
除了上诉的1范数,2范数,另一个常用的矩阵范数是核范数,给定矩阵 A ∈ R m ∗ n A{\in}R^{m*n} A∈Rm∗n,核范数定义为
∣ ∣ A ∣ ∣ ∗ = ∑ i = 1 r σ i ||A||_*=\sum_{i=1}^r{\sigma}_i ∣∣A∣∣∗=i=1∑rσi
其中 σ i , i = 1 , 2 , . . . , r {\sigma}_i,i=1,2,...,r σi,i=1,2,...,r为 A A A的所有非0奇异值, r = r a n k ( A ) r=rank(A) r=rank(A),类似于向量的 l 1 l_1 l1范数可以保稀疏性,我们也通常通过限制矩阵的核范数来保证矩阵的低秩性。
2.1.3 矩阵内积
内积一般用来表征两个矩阵之间的夹角,一个常用的内积—Frobenius内积, m ∗ n m*n m∗n的矩阵 A A A和 B B B的Frobenius内积定义为
< A , B > = T r ( A B T ) = ∑ i = 1 m ∑ j = 1 n a i j b i j <A,B>=Tr(AB^T)=\sum_{i=1}^m\sum_{j=1}^na_{ij}b_{ij} <A,B>=Tr(ABT)=i=1∑mj=1∑naijbij
其实就是两个矩阵一一对应元素相乘
同样的,我们也有矩阵范数对应的柯西不等式,设 A , B ∈ R m ∗ n A,B{\in}R^{m*n} A,B∈Rm∗n,则
∣ < A , B > ∣ < = ∣ ∣ A ∣ ∣ F ∣ ∣ B ∣ ∣ F |<A,B>|<=||A||_F||B||_F ∣<A,B>∣<=∣∣A∣∣F∣∣B∣∣F
等号成立当且仅当A和B线性相关
2.2 导数
2.2.1 梯度与海瑟矩阵
梯度的定义(这玩意应该是我之前好像都没见到过的):给定函数 f : R n → R f:R^n{\rightarrow}R f:Rn→R,且 f f f在点 x x x的一个邻域内有意义,若存在向量 g ∈ R n g{\in}R^n g∈Rn满足
lim p → 0 f ( x + p ) − f ( x ) − g T p ∣ ∣ p ∣ ∣ = 0 \lim_{p{\rightarrow}0}\frac{f(x+p)-f(x)-g^Tp}{||p||}=0 p→0lim∣∣p∣∣f(x+p)−f(x)−gTp=0
就称 f f f在点 x x x处可微,此时 g g g称为 f f f在点 x x x处的梯度,记作 ∇ f ( x ) {\nabla}f(x) ∇f(x),如果对区域D上的每一个点 x x x都有 ∇ f ( x ) {\nabla}f(x) ∇f(x)存在,则称 f f f在D上可微
然后呢,这其中经过一系列的推导,就可以得到我们耳熟能详的梯度公式
∇ f ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , . . . , ∂ f ( x ) ∂ x m ] T {\nabla}f(x)=\left[ \begin{matrix} {\frac{{\partial}f(x)}{{\partial}x_1}} ,{\frac{{\partial}f(x)}{{\partial}x_2}} ,...,{\frac{{\partial}f(x)}{{\partial}x_m}} \end{matrix} \right]^T ∇f(x)=[∂x1∂f(x),∂x2∂f(x),...,∂xm∂f(x)]T
对于多元函数,我们可以定义其海瑟矩阵:如果函数 f ( x ) : R n → R f(x):R^n{\rightarrow}R f(x):Rn→R在点 x x x处的二阶偏导数 ∂ 2 f ( x ) ∂ x i ∂ x j i , j = 1 , 2 , . . . , n \frac{{\partial}^2f(x)}{{\partial}x_i{\partial}x_j}i,j=1,2,...,n ∂xi∂xj∂2f(x)i,j=1,2,...,n都存在,则
∇ 2 f ( x ) = [ ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x 1 ∂ x n ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 ⋯ ∂ 2 f ( x ) ∂ x 2 ∂ x n ⋮ ⋮ ⋮ ∂ 2 f ( x ) ∂ x n ∂ x 1 ∂ 2 f ( x ) ∂ x n ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x n 2 ] {\nabla}^2f(x)=\left[ \begin{matrix} \frac{{\partial}^2f(x)}{{\partial}x_1^2} & \frac{{\partial}^2f(x)}{{\partial}x_1{\partial}x_2} & \cdots& \frac{{\partial}^2f(x)}{{\partial}x_1{\partial}x_n}\\ \frac{{\partial}^2f(x)}{{\partial}x_2{\partial}x_1} &\frac{{\partial}^2f(x)}{{\partial}x_2^2} & \cdots & \frac{{\partial}^2f(x)}{{\partial}x_2{\partial}x_n} \\ \vdots & \vdots & &\vdots\\ \frac{{\partial}^2f(x)}{{\partial}x_n{\partial}x_1} &\frac{{\partial}^2f(x)}{{\partial}x_n{\partial}x_2} & \cdots &\frac{{\partial}^2f(x)}{{\partial}x_n^2} \end{matrix} \right] ∇2f(x)= ∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)⋯⋯⋯∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)
成为 f f f在点 x x x处的海瑟矩阵
当 ∇ 2 f ( x ) {\nabla}^2f(x) ∇2f(x)在区域D上每个点 x x x都存在,就称 f f f在D上二阶可微,若他在D上还连续,可以证明此时的海瑟矩阵是一个对称矩阵
当 f : R n → R m f:R^n{\rightarrow}R^m f:Rn→Rm是向量值函数时,我们可以定义他的雅可比矩阵 J ( x ) ∈ R m ∗ n J(x){\in}R^{m*n} J(x)∈Rm∗n,他的第i行分量 f i ( x ) f_i(x) fi(x)梯度的转置,即
J ( x ) = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 1 ( x ) ∂ x 2 ⋯ ∂ f 1 ( x ) ∂ x n ∂ f 2 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 2 ⋯ ∂ f 2 ( x ) ∂ x n ⋮ ⋮ ⋮ ∂ f m ( x ) ∂ x 1 ∂ f m ( x ) ∂ x 2 ⋯ ∂ f m ( x ) ∂ x n ] J(x)=\left[ \begin{matrix} \frac{{\partial}f_1(x)}{{\partial}x_1} & \frac{{\partial}f_1(x)}{{\partial}x_2} & \cdots& \frac{{\partial}f_1(x)}{{\partial}x_n}\\ \frac{{\partial}f_2(x)}{{\partial}x_1} & \frac{{\partial}f_2(x)}{{\partial}x_2} & \cdots& \frac{{\partial}f_2(x)}{{\partial}x_n}\\ \vdots & \vdots & &\vdots\\ \frac{{\partial}f_m(x)}{{\partial}x_1} & \frac{{\partial}f_m(x)}{{\partial}x_2} & \cdots& \frac{{\partial}f_m(x)}{{\partial}x_n} \end{matrix} \right] J(x)= ∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)⋮∂x2∂fm(x)⋯⋯⋯∂xn∂f1(x)∂xn∂f2(x)⋮∂xn∂fm(x)
容易看出,梯度 ∇ f ( x ) {\nabla}f(x) ∇f(x)的雅可比矩阵就是f(x)的海瑟矩阵
类似于一元函数的泰勒展开,对于多元函数,这里也不加证明的给出泰勒展开
设 f : R n → R f:R^n{\rightarrow}R f:Rn→R是连续可微的, p ∈ R n p{\in}R^n p∈Rn,那么
f ( x + p ) = f ( x ) + ∇ ( x + t p ) T p f(x+p)=f(x)+{\nabla}(x+tp)^Tp f(x+p)=f(x)+∇(x+tp)Tp
其中 0 < t < 1 0<t<1 0<t<1,进一步,如果说 f f f是二阶连续可微的
f ( x + p ) = f ( x ) + ∇ f ( x ) T p + 1 2 p T ∇ 2 f ( x + t p ) p f(x+p)=f(x)+{\nabla}f(x)^Tp+\frac{1}{2}p^T{\nabla}^2f(x+tp)p f(x+p)=f(x)+∇f(x)Tp+21pT∇2f(x+tp)p
其中 0 < t < 1 0<t<1 0<t<1
最后呢这一章还介绍了一类特殊的可微函数-----梯度利普希茨连续的函数,这类函数在很多优化算法收敛性证明中起着关键作用
梯度利普希茨连续定义:给定可微函数 f f f,若存在 L > 0 L>0 L>0,对任意 x , y ∈ d o m f x,y{\in}domf x,y∈domf有( d o m f domf domf就是 f f f的定义域)
∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ≤ L ∣ ∣ x − y ∣ ∣ ||{\nabla}f(x)-{\nabla}f(y)||{\le}L||x-y|| ∣∣∇f(x)−∇f(y)∣∣≤L∣∣x−y∣∣
则称 f f f是梯度利普希茨连续的,相应利普希茨常数为 L L L,有时候也会称为 L L L-光滑,或者梯度 L L L-利普希茨连续
梯度利普希茨连续表明, ∇ f ( x ) {\nabla}f(x) ∇f(x)的变化可以被自变量 x x x的变化所控制,满足该性质的函数有很多很好的性质, 一个重要的性质就是具有二次上界
具体证明我这里我就不再过多阐述了,有二次上界就是说 f ( x ) f(x) f(x)可以被一个二次函数上界所控制,即要求说 f ( x ) f(x) f(x)的增长速度不超过二次
还有一个推论就是说,如果 f f f是梯度利普希茨连续的,且有一个全局最小点 x ∗ x^* x∗,我们可以利用二次上界来估计 f ( x ) − f ( x ∗ ) f(x)-f(x^*) f(x)−f(x∗)的大小,其中 x x x可以是定义域中任意一点
1 2 L ∣ ∣ ∇ f ( x ) ∣ ∣ 2 ≤ f ( x ) − f ( x ∗ ) \frac{1}{2L}||{\nabla}f(x)||^2{\le}f(x)-f(x^*) 2L1∣∣∇f(x)∣∣2≤f(x)−f(x∗)
具体的证明我这里就不写了哈,想知道的可以百度或者我们讨论一下
2.2.2 矩阵变量函数的导数
多元函数梯度的定义也可以推广到变量是矩阵的情况,以 m ∗ n m*n m∗n矩阵 X X X为自变量的函数 f ( X ) f(X) f(X),若存在矩阵 G ∈ R m ∗ n G{\in}R^{m*n} G∈Rm∗n满足
lim V → 0 f ( X + V ) − f ( X ) − < G , V > ∣ ∣ V ∣ ∣ = 0 \lim_{V{\rightarrow}0}\frac{f(X+V)-f(X)-<G,V>}{||V||}=0 V→0lim∣∣V∣∣f(X+V)−f(X)−<G,V>=0
其中 ∣ ∣ ⋅ ∣ ∣ ||·|| ∣∣⋅∣∣是任意矩阵范数,就称矩阵向量函数 f f f在 X X X处 F r a ˊ c h e t Fr\acute{a}chet Fraˊchet可微,就称G为 f f f在 F r a ˊ c h e t Fr\acute{a}chet Fraˊchet可微意义下的梯度,其实矩阵变量函数 f ( X ) f(X) f(X)的梯度也可以用其偏导数表示为
∇ f ( x ) = [ ∂ f ∂ x 11 ∂ f ∂ x 12 ⋯ ∂ f ∂ x 1 n ∂ f ∂ x 21 ∂ f ∂ x 22 ⋯ ∂ f ∂ x 2 n ⋮ ⋮ ⋮ ∂ f ∂ x m 1 ∂ f ∂ x m 2 ⋯ ∂ f ∂ x m n ] {\nabla}f(x)=\left[ \begin{matrix} \frac{{\partial}f}{{\partial}x_{11}} & \frac{{\partial}f}{{\partial}x_{12}} & \cdots& \frac{{\partial}f}{{\partial}x_{1n}}\\ \frac{{\partial}f}{{\partial}x_{21}} & \frac{{\partial}f}{{\partial}x_{22}} & \cdots& \frac{{\partial}f}{{\partial}x_{2n}}\\ \vdots & \vdots & &\vdots\\ \frac{{\partial}f}{{\partial}x_{m1}} & \frac{{\partial}f}{{\partial}x_{m2}} & \cdots& \frac{{\partial}f}{{\partial}x_{mn}} \end{matrix} \right] ∇f(x)= ∂x11∂f∂x21∂f⋮∂xm1∂f∂x12∂f∂x22∂f⋮∂xm2∂f⋯⋯⋯∂x1n∂f∂x2n∂f⋮∂xmn∂f
F r a ˊ c h e t Fr\acute{a}chet Fraˊchet可微的定义和使用往往比较繁琐,为此还有另一种定义----- G a ^ t e a u x G\hat{a}teaux Ga^teaux可微
定义:设 f ( X ) f(X) f(X)为矩阵变量函数,如果存在矩阵 G ∈ R m ∗ n G{\in}R^{m*n} G∈Rm∗n对任意方向 V ∈ R m ∗ n V{\in}R^{m*n} V∈Rm∗n满足
lim t → 0 f ( X + t V ) − f ( X ) − t < G , V > t = 0 \lim_{t{\rightarrow}0}\frac{f(X+tV)-f(X)-t<G,V>}{t}=0 t→0limtf(X+tV)−f(X)−t<G,V>=0
则称 f f f关于 X X X是 G a ^ t e a u x G\hat{a}teaux Ga^teaux的,就称G为 f f f在 G a ^ t e a u x G\hat{a}teaux Ga^teaux可微意义下的梯度
若 F r a ˊ c h e t Fr\acute{a}chet Fraˊchet可微可以推出 G a ^ t e a u x G\hat{a}teaux Ga^teaux可微,反之则不可以,但这本书讨论的函数基本都是 F r a ˊ c h e t Fr\acute{a}chet Fraˊchet可微的,所以我们目前无需讨论,大家了解一下就好了~,统一将矩阵变量函数 f ( X ) f(X) f(X)的导数记为 ∂ f ∂ X \frac{{\partial}f}{{\partial}X} ∂X∂f或者 ∇ f ( X ) {\nabla}f(X) ∇f(X)
举个例子把,免得大家不知道有什么用
考虑线性函数: f ( X ) = T r ( A X T B ) f(X)=Tr(AX^TB) f(X)=Tr(AXTB),其中 A ∈ R p ∗ n , B ∈ R m ∗ p , X ∈ R m ∗ n A{\in}R^{p*n},B{\in}R^{m*p},X{\in}R^{m*n} A∈Rp∗n,B∈Rm∗p,X∈Rm∗n对任意方向 V ∈ R m ∗ n V{\in}R^{m*n} V∈Rm∗n以及 t ∈ R t{\in}R t∈R,有
lim t → 0 f ( X + t V ) − f ( X ) t = lim t → 0 T r ( A ( X + t V ) T B − T r ( A X T B ) ) t \lim_{t{\rightarrow}0}\frac{f(X+tV)-f(X)}{t}=\lim_{t{\rightarrow}0}\frac{Tr(A(X+tV)^TB-Tr(AX^TB))}{t} t→0limtf(X+tV)−f(X)=t→0limtTr(A(X+tV)TB−Tr(AXTB))
= T r ( A V T B ) = < B A , V > =Tr(AV^TB)=<BA,V> =Tr(AVTB)=<BA,V>
所以, ∇ f ( X ) = B A {\nabla}f(X)=BA ∇f(X)=BA
我学到这里时候会有一个疑问,就是 T r ( A V T B ) = < B A , V > Tr(AV^TB)=<BA,V> Tr(AVTB)=<BA,V>是为什么呢?
我们知道, T r ( A V T B ) = T r ( B A V T ) Tr(AV^TB)=Tr(BAV^T) Tr(AVTB)=Tr(BAVT)这个是迹的基本性质, B A BA BA和 V V V都是 m ∗ n m*n m∗n的,那么这时候又有一个性质,假设C和D是相同规模的矩阵,那么 T r ( A T B ) = < A , B > Tr(A^TB)=<A,B> Tr(ATB)=<A,B>
我这里是参考知乎jordi的,这是他的一个关于3*3矩阵的推导
链接:https://www.zhihu.com/question/274052744/answer/1521521561

那么这样就可以推出 T r ( A V T B ) = T r ( V T , B A ) = < B A , V > Tr(AV^TB)=Tr(V^T,BA)=<BA,V> Tr(AVTB)=Tr(VT,BA)=<BA,V>啦
2.2.3 自动微分
自动微分是使用计算机导数的算法,在神经网络中,我们通过前向传播的方式将输入数据 a a a转化为 y ^ \hat{y} y^,也就是将输入数据 a a a作为初始信息,将其传递到隐藏层的每个神经元,处理后输出得到 y ^ \hat{y} y^。
通过比较输出得到 y ^ \hat{y} y^与真实标签y,可以定义一个损失函数 f ( x ) f(x) f(x),其中 x x x表示所有神经元对饮的参数集合, f ( x ) f(x) f(x)一般是多个函数复合的形式,为了找到最优的参数,我们需要通过优化算法来调整 x x x使得 f ( x ) f(x) f(x)达到最小,因此,对神经元参数 x x x的计算是不可避免的
这一块就是讲了一个神经网络的前向传播和后向求导,自动微分有两种方式,前向模式和后向模式,前向模式就是变传播变求导,后向模式就是前传播再一层层求导,很显然现在大家学的都是后向模式这种的吧,因为他复杂度更低,计算代价小
2.3 广义实值函数
数学分析的课程中我们学习了函数的基本概念,函数是从向量空间 R n R^n Rn到数据域 R R R的映射,而在最优化领域,经常涉及到对某个函数的某一个变量取inf(sup)操作,这导致函数的取值可能为无穷,为了能更方便的描述优化问题,我们需要对函数的定义进行某种扩展。
那么 what is 广义实值函数呢?
令 R ˉ = R ⋃ ∞ \bar{R}=R{\bigcup}{\infty} Rˉ=R⋃∞为广义实数空间,则映射 f : R n → R ˉ f:R^n{\rightarrow}\bar{R} f:Rn→Rˉ称为广义实值函数,可以看到,就是值域多了两个特殊的值,正负无穷
2.3.1 适当函数
适当函数:给定广义实值函数 f f f和非空集合 X X X,如果存在 x ∈ X x{\in}X x∈X使得 f ( x ) < + ∞ f(x)<+{\infty} f(x)<+∞,并且对任意的 x ∈ X x{\in}X x∈X,都有 f ( x ) > − ∞ f(x)>-{\infty} f(x)>−∞,那么称函数 f f f关于集合 X X X是适当的
总结一下,就是说适当函数 f f f呢,至少有一处的取值不为正无穷,以及处处取值不为负无穷。对于最优化问题,适当函数可以帮助我们去掉一些不感兴趣的函数,从一个比较合理的函数类去考虑问题。这应该很好理解,我们加入讨论一个min问题,他至少有个取值不能为正无穷吧,要不然怎么取min,然后处处取值不能为负无穷,要不讨论有啥意义对吧?
我们约定,若本书无特殊说明,定理中所讨论的函数均为适当函数
对于适当函数 f f f,规定其定义域
d o m f = { x ∣ f ( x ) < + ∞ } domf=\{x|f(x)<+{\infty}\} domf={x∣f(x)<+∞}
因为对于适当函数的最小值肯定不可能在正无穷处取到^^
2.3.2 闭函数
闭函数是另一类重要的广义实值函数,闭函数可以看作是连续函数的一种推广
在说闭函数之前,我们先引入一些基本概念:
1.下水平集
下水平集是描述实值函数取值的一个重要概念:为此有如下定义
( α \alpha α-下水平集)对于广义实值函数: f : R n → R ˉ f:R^n{\rightarrow}\bar{R} f:Rn→Rˉ
C α = { x ∣ f ( x ) ≤ α } C_{\alpha}=\{x|f(x)\le{\alpha}\} Cα={x∣f(x)≤α}
称为 f f f的 α \alpha α-下水平集
就是取值不能超过 α \alpha α嘛,若 C α C_{\alpha} Cα非空,我们知道 f ( x ) f(x) f(x)的全局最小点一定落在 C α C_{\alpha} Cα中,无需考虑之外的点
2.上方图
上方图是从集合的角度来描述一个函数的具体性质,有如下定义:
对于广义实值函数 f : R n → R ˉ f:R^n{\rightarrow}\bar{R} f:Rn→Rˉ
e p i f = { ( x , t ) ∈ R n + 1 ∣ f ( x ) ≤ t } epif=\{(x,t){\in}R^{n+1}|f(x){\le}t\} epif={(x,t)∈Rn+1∣f(x)≤t}
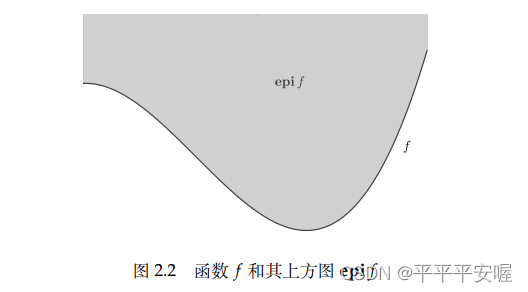
说人话就是函数 f f f上方的东西小于等于t(t取任意值), f f f的很多性质都可以通过 e p i f epif epif得到,可以通过 e p i f epif epif的一些性质 f f f的性质
3.闭函数、下半连续函数
闭函数:设 f : R n → R ˉ f:R^n{\rightarrow}\bar{R} f:Rn→Rˉ为广义实值函数,若 e p i f epif epif为闭集,则称 f f f为闭函数
下半连续函数:设广义实值函数 f : R n → R ˉ f:R^n{\rightarrow}\bar{R} f:Rn→Rˉ,若对任意的 x ∈ R n x{\in}R^n x∈Rn,有
lim inf y → x f ( y ) ≥ f ( x ) \liminf_{y{\rightarrow}x} f(y)\ge{f(x)} y→xliminff(y)≥f(x)
则 f ( x ) f(x) f(x)为下半连续函数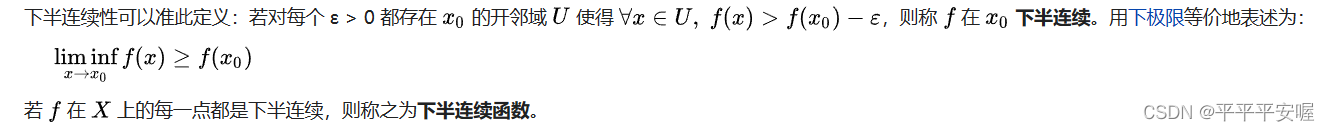
我觉得如果不懂这个下极限的话,直接看文字会好得多
其实就是在 x 0 x_0 x0处的邻域处,如果 f( x 0 x_0 x0) 减去一个正的微小值,从而可以恒小于该邻域的所有 f ( x ) f(x) f(x),则称在该间断点处有下半连续性。
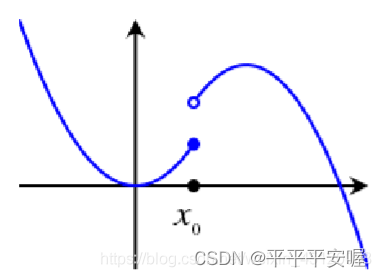
如果是下图这样的
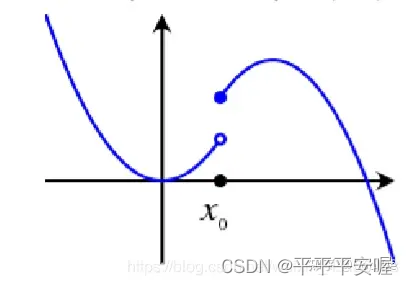
你的 x 0 x_0 x0再往左边取哪怕一点点,都会骤降,就达不到 x 0 x_0 x0的邻域中的 x x x比 f ( x 0 ) − ε f(x_0)-{\varepsilon} f(x0)−ε大,而如果是第一张图,我们可以保证 x 0 x_0 x0的左边不会骤降,差不多就是这个意思
设广义实值函数 f : R n → R ˉ f:R^n{\rightarrow}\bar{R} f:Rn→Rˉ。则以下命题等价:
(1) f ( x ) f(x) f(x)的任意 α \alpha α-下水平集都是闭集
(2) f ( x ) f(x) f(x)是下半连续的
(3) f ( x ) f(x) f(x)是闭函数
具体证明我就不在这细细展开了,同理,想知道可以和我探讨或者自行谷歌~
闭集: 如果对任意收敛序列,最终收敛到的点都在集合内,那么集合是闭的
我们可以看到,其实闭函数和下半连续函数可以等价,以后往往只会出现一种定义
闭(下半连续)函数间的简单运算会保持原有性质
(1)加法,若 f f f和 g g g均为适当的闭函数,并且 d o m f ⋂ d o m g ≠ ∅ domf {\bigcap}domg{\neq}∅ domf⋂domg=∅则 f + g f+g f+g也是闭函数,说是适当是避免出现未定式的情况,也就是负无穷+正无穷
(2)仿射映射的复合,若 f f f为闭函数,则 f ( A x + b ) f(Ax+b) f(Ax+b)也为闭函数
(3)取上确界,若每一个函数 f α f_{\alpha} fα均为闭函数,则 s u p α f α ( x ) sup_{\alpha}f_{\alpha}(x) supαfα(x)也为闭函数。
2.4 凸集
2.4.1 凸集的相关定义
说实话凸集这个之前说的一直都有听说,但是具体的定义我一直没有搞明白,现在学一下~
对于 R n R^n Rn中的两个点 x 1 ≠ x 2 x_1{\neq}x2 x1=x2,形如
y = θ x 1 + ( 1 − θ ) x 2 y={\theta}x_1+(1-{\theta})x_2 y=θx1+(1−θ)x2
的点形成了过点 x 1 x_1 x1和 x 2 x_2 x2的直线,当 0 ≤ θ ≤ 1 0{\le}{\theta}{\le}1 0≤θ≤1时,这样的点形成了连接点 x 1 x_1 x1与 x 2 x_2 x2的线段
我们定义:如果过集合 C C C中任意两点的直线都在 C C C内,则称 C C C为仿射集,即
x 1 , x 2 ∈ C ⟶ θ x 1 + ( 1 − θ ) x 2 ∈ C , ∀ θ ∈ R x_1,x_2{\in}C{\longrightarrow}{\theta}x_1+(1-{\theta})x_2{\in}C,{\forall}{\theta}{\in}R x1,x2∈C⟶θx1+(1−θ)x2∈C,∀θ∈R
很明显可以看出,线性方程组 A x = b Ax=b Ax=b的解集是仿射集,反之,任意仿射集都可以表示成一个线性方程组的解集
那么,凸集是定义是什么呢?
凸集:如果连接集合 C C C中任意两点的线段都在 C C C内,则称 C C C为凸集,即
x 1 , x 2 ∈ C ⟶ θ x 1 + ( 1 − θ ) x 2 ∈ C , ∀ 0 ≤ θ ≤ 1 x_1,x_2{\in}C{\longrightarrow}{\theta}x_1+(1-{\theta})x_2{\in}C,{\forall}0{\le}{\theta}{\le}1 x1,x2∈C⟶θx1+(1−θ)x2∈C,∀0≤θ≤1
可以看到凸集就是仿射集的直线变成线段了而已,仿射集都是凸集
从凸集我们可以引出凸组合和凸包的概念,形如
x = θ 1 x 1 + θ 2 x 2 + ⋯ + θ k x k x={\theta}_1x_1+{\theta}_2x_2+\cdots+{\theta}_kx_k x=θ1x1+θ2x2+⋯+θkxk
1 = θ 1 + θ 2 + ⋯ + θ k , θ i ≥ 0 , i = 1 , 2 , ⋯ , k 1={\theta}_1+{\theta}_2+\cdots+{\theta}_k,{\theta}_i{\ge}0,i=1,2,\cdots,k 1=θ1+θ2+⋯+θk,θi≥0,i=1,2,⋯,k
的点称为 x 1 , x 2 , ⋯ , x k x_1,x_2,\cdots,x_k x1,x2,⋯,xk的凸组合,集合 S S S中点所有的凸组合构成的集合称为 S S S的凸包,记作 c o n v S conv S convS,简而言之, c o n v S convS convS是包含 S S S的最小的凸集
若在凸组合的定义中去掉 θ i ≥ 0 {\theta}_i{\ge}0 θi≥0的限制,我们可以得到仿射包的概念
仿射包:设 S S S为 R n R^n Rn的子集,称如下集合为S的仿射包:
{ x ∣ x = x = θ 1 x 1 + θ 2 x 2 + ⋯ + θ k x k , x 1 , x 2 , ⋯ , x k ∈ S , θ 1 + θ 2 + ⋯ + θ k = 1 } \{x|x=x={\theta}_1x_1+{\theta}_2x_2+\cdots+{\theta}_kx_k, x_1,x_2,\cdots,x_k{\in}S,{\theta} _1+{\theta}_2+\cdots+{\theta}_k=1\} {x∣x=x=θ1x1+θ2x2+⋯+θkxk,x1,x2,⋯,xk∈S,θ1+θ2+⋯+θk=1}
记为 a f f i n e S affineS affineS
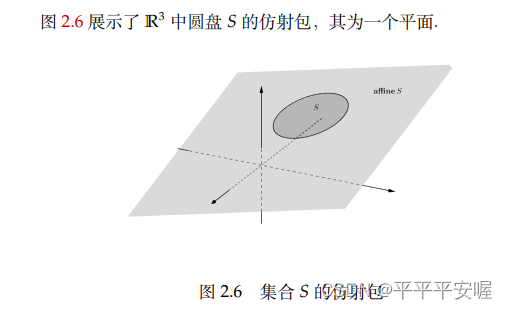 fangshebao
fangshebao
一般而言,一个集合的仿射包实际上是包含该集合的最小的仿射集
形如
x = θ 1 x 1 + θ 2 x 2 , θ 1 > 0 , θ 2 > 0 x={\theta}_1x_1+{\theta}_2x_2,{\theta}_1>0,{\theta}_2>0 x=θ1x1+θ2x2,θ1>0,θ2>0
的点称为点 x 1 , x 2 x_1,x_2 x1,x2的锥组合,若集合 S S S的任意点的锥组合都在 S S S中,则称S为凸锥
2.4.2 重要的凸集
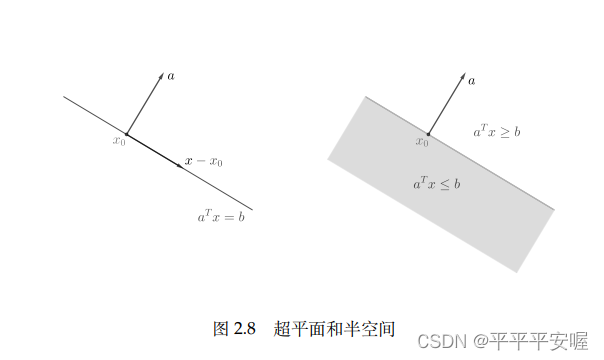
1.超平面和半空间
任取非零向量 a a a,形如 { x ∣ a T x = b } \{x|a^Tx=b\} {x∣aTx=b}的集合称为超平面,形如 { x ∣ a T x ≤ b } \{x|a^Tx{\le}b\} {x∣aTx≤b}的集合称为半空间, a a a是对应的超平面和半空间的法向量,一个超平面将 R n R^n Rn分为两个半空间,容易看出,超平面是仿射集和凸集,半空间是凸集但不是仿射集(这个如果理解了仿射集和凸集的概念应该很好理解)
2.球、椭球、锥
球和椭球也是常见的凸集,球我们这里就不多介绍了
形如
{ x ∣ ( x − x c ) T P − 1 ( x − x ) c ) ≤ 1 } \{x|(x-x_c)^TP^{-1}(x-x)_c){\le}1\} {x∣(x−xc)TP−1(x−x)c)≤1}
的集合称为椭球,其中P对称正定,椭球的另一种表示为 { x c + A u ∣ ∣ u 2 ∣ ∣ ≤ 1 } \{x_c+Au||u_2||{\le}1\} {xc+Au∣∣u2∣∣≤1},A为非奇异的方阵
另外,我们称集合
{ ( x , t ) ∣ ∣ ∣ x ∣ ∣ ≤ t } \{(x,t)|||x||{\le}t\} {(x,t)∣∣∣x∣∣≤t}
为范数锥,欧几里得范数锥也称为二次锥,范数锥是凸集
别忘了 t t t也是变量噢,看这个图应该就很好理解范数锥了
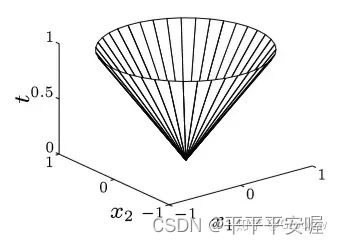
知乎链接:https://zhuanlan.zhihu.com/p/126072881
3.多面体
我们把满足线性等式和不等式组的点的集合称为多面体,即
{ x ∣ A x ≤ b , C x = d } \{x|Ax{\le}b,Cx=d\} {x∣Ax≤b,Cx=d}
多面体是有限个半空间和超平面的交集,所以是凸集
4.(半)正定锥
这个我直接把书上的先贴过来把,我目前也不太懂,就不能细说
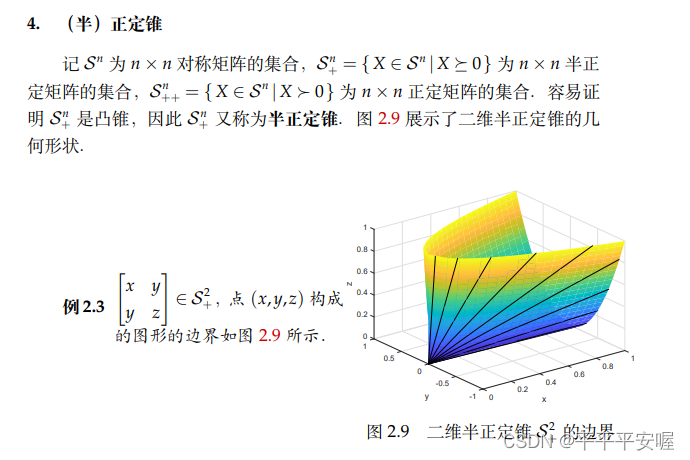
2.4.3 保凸的运算
证明一个集合是凸集有两种方式,第一种就是利用定义
x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 ⟶ θ x 1 + ( 1 − θ x 2 ∈ C ) x_1,x_2{\in}C,0{\le}{\theta}{\le}1{\longrightarrow}{\theta}x_1+(1-{\theta}x_2{\in}C) x1,x2∈C,0≤θ≤1⟶θx1+(1−θx2∈C)来证明集合 C C C是凸集。
第二种方法就是说明集合C可以由简单的凸集(刚刚说的超平面、半空间,范数球等)经过保凸的运算得到。
定理1:任意多个凸集的交为凸集
定理2:设 f : R n → R m f:R^n{\rightarrow}R^m f:Rn→Rm是仿射变换( f ( x ) = A x + b , A ∈ R m ∗ n , b ∈ R n f(x)=Ax+b,A{\in}R^{m*n},b{\in}R^n f(x)=Ax+b,A∈Rm∗n,b∈Rn),则
(1)凸集在 f f f下的像是凸集:
S 是凸集 → f ( S ) → { f ( x ) ∣ x ∈ S } 是凸集 S是凸集{\rightarrow}f(S){\rightarrow}\{f(x)|x{\in}S\}是凸集 S是凸集→f(S)→{f(x)∣x∈S}是凸集
(2)凸集在 f f f下的原像是凸集
C 是凸集 → f − 1 ( C ) → { x ∈ R n ∣ f ( x ) ∈ C } 是凸集 C是凸集{\rightarrow}f^{-1}(C){\rightarrow}\{x{\in}R^n|f(x){\in}C\}是凸集 C是凸集→f−1(C)→{x∈Rn∣f(x)∈C}是凸集
就是经过缩放、平移或者投像仍是凸集
2.4.4 分离超平面定理
这是一个凸集的重要性质,即可以用超平面分离不相交的凸集,最基本的结果是分离超平面定理和支撑超平面定理
分离超平面定理:如果C和D是不相交的两个凸集,则存在非零向量 a a a和常熟 b b b,使得
a T x ≤ b , ∀ x ∈ C , 且 a T x ≥ b , ∀ x ∈ D a^Tx{\le}b,{\forall}x{\in}C,且a^Tx{\ge}b,{\forall}x{\in}D aTx≤b,∀x∈C,且aTx≥b,∀x∈D
即超平面 { x ∣ a T x = b } \{x|a^Tx=b\} {x∣aTx=b}分离了 C C C和 D D D
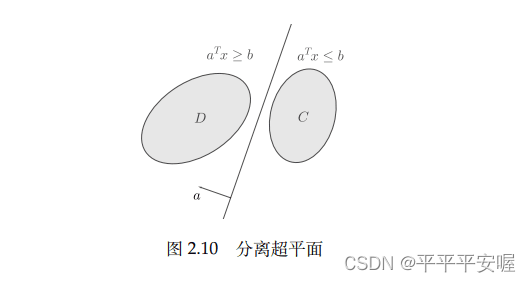
严格分离定理:即上述成立严格不等号,具体我就不展开了
支撑超平面:给定集合 C C C及其边界上一点 x 0 x_0 x0,如果 a ≠ 0 a{\neq}0 a=0满足 a T x ≤ a T x 0 , ∀ x ∈ C a^Tx{\le}a^Tx_0,{\forall}x{\in}C aTx≤aTx0,∀x∈C,那么称集合
{ x ∣ a T x = a T x 0 } \{x|a^Tx=a^T{x_0}\} {x∣aTx=aTx0}
为 C C C在边界点 x 0 x_0 x0处的支撑超平面
从几何上来说,此超平面与集合 C C C在点 x 0 x_0 x0处相切
支撑超平面定理:如果C是凸集,则在C的任意边界点处都存在支撑超平面
这个定理其实有非常强的几何直观,就是给定一个平面后,可以把凸集边界上的任意一点当成支撑点将凸集放在该平面上,其他形状的集合一般没有这个性质。
相关文章:

最优化:建模、算法与理论
最优化:建模、算法与理论 目前在学习 最优化:建模、算法与理论这本书,来此记录一下,顺便做一些笔记,在其中我也会加一些自己的理解,尽量写的不会那么的条条框框(当然最基础的还是要有ÿ…...
拿捏--->打印菱形
文章目录 题目描述算法思路代码示例 题目描述 在屏幕上输出以下图案: 算法思路 代码示例 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> int main() {int n;scanf("%d", &n);//上半部分菱形for (int i 0; i < n; i) //上半部分…...
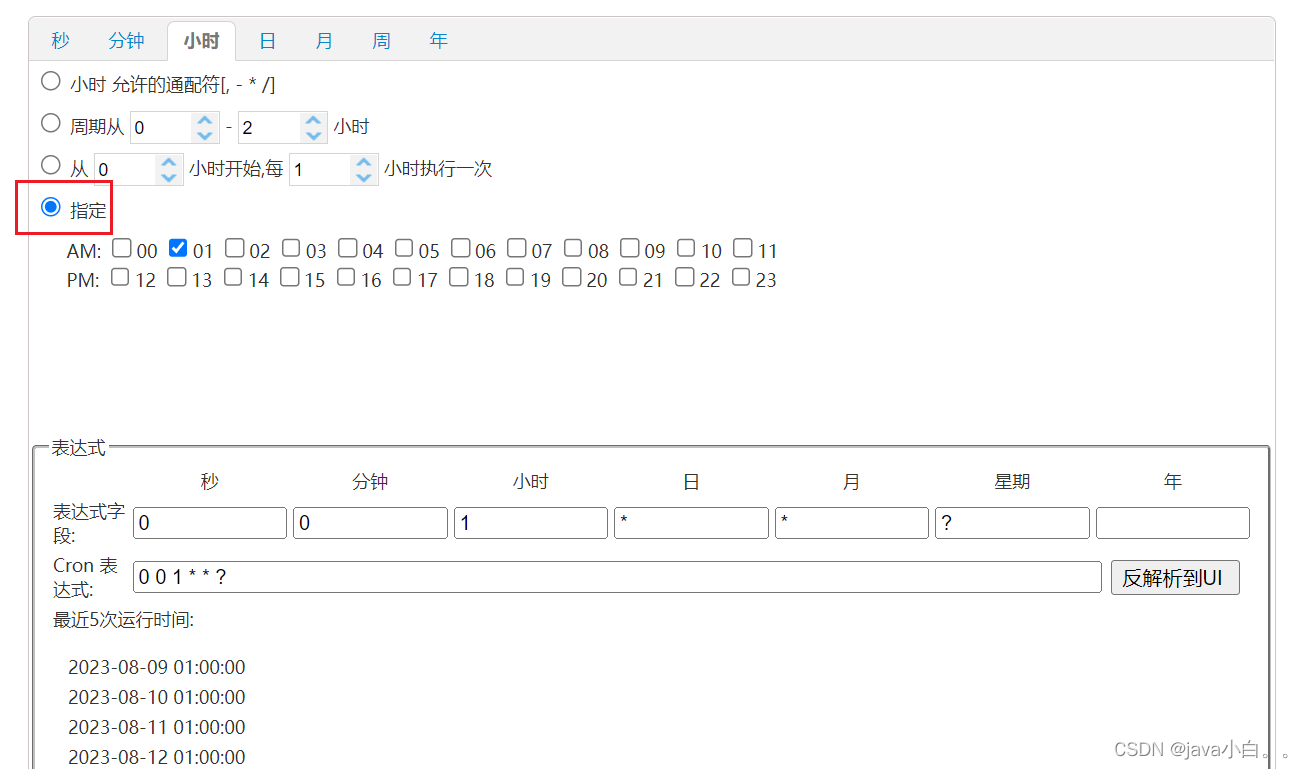
【SpringBoot笔记】定时任务(cron)
定时任务就是在固定的时间执行某个程序,闹钟的作用。 1.在启动类上添加注解 EnableScheduling 2.创建定时任务类 在这个类里面使用表达式设置什么时候执行 cron 表达式(也叫七子表达式),设置执行规则 package com.Lijibai.s…...
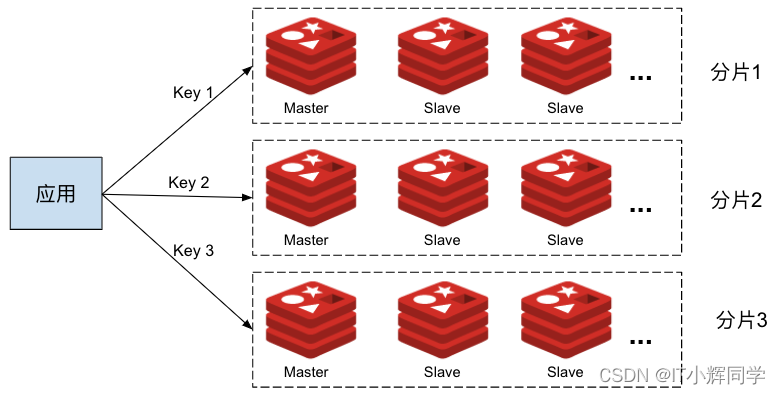
Redis单机,主从,哨兵,集群四大模式
Redis 单机模式 Redis 单机模式是指 Redis 数据库在单个服务器上以独立的、单一的进程运行的模式。在这种模式下,Redis 不涉及数据分片或集群配置,所有的数据和操作都在一个实例中进行。以下是关于 Redis 单机模式的详细介绍: 单一实例&#…...
2023年8月份华为H12-811更新了
801、[单选题]178/832、在系统视图下键入什么命令可以切换到用户视图? A quit B souter C system-view D user-view 试题答案:A 试题解析:在系统视图下键入quit命令退出到用户视图。因此答案选A。 802、[单选题]“网络管理员在三层交换机上创建了V…...
[K8S:命令执行:权限异常:解决篇]:通过更新kubeconfig配置相关信息
文章目录 一:场景复现:1.1:关键信息:1.2:全异常日志输出: 二:解决流程:2.1:更新 kubeconfig:2.1.1:执行命令: 2.2:再次执行…...
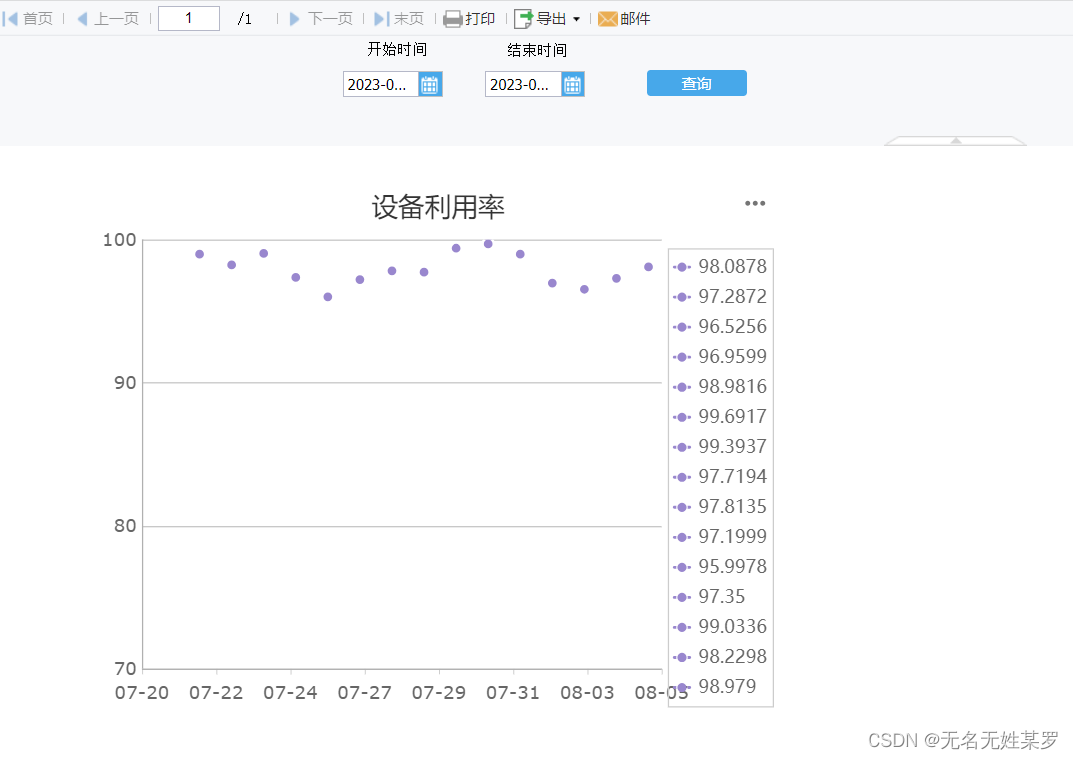
帆软设计器报表加载不出折线图的原因
最近在用帆软设计器做可视化图表。偶有遇到因为数据集的字段类型导致加载不出折线,现记录如下。做报表的同行可以参考。 数据库使用了 Oracle 11g。数据集的 SQL 代码片是之前用在另一个单元格报表里面的。页面上有一个率是直接计算得出,我为了方便、就…...

[QCA6174]sdx12平台WiFi QCA6174在驱动加载的时候增加模块参数方法
需求描述 由于开发需要,有时候需要在驱动模块加载的时候增加一个参数,传递给到驱动使用 平台描述 Qualcomm SDX12+QCA6174平台 驱动信息 [ 112.281429] wlan: loading driver v4.0.11.213X [ 112.340262] msm_pcie_enable: PCIe: Assert the reset of endpoint of RC0. …...
Ajax-AJAX请求的不同发送方式
🥔:你一定能成为想要成为的人 发送AJAX请求不同方式 发送AJAX请求不同方式1、jQuery发送AJAX请求2、axios发送AJAX请求(重点)3、fetch发送AJAX请求 发送AJAX请求不同方式 1、jQuery发送AJAX请求 首先需要jquery的js文件…...

简易图书管理系统(面向对象思想)
目录 前言 1.整体思路 2.Book包 2.1Book类 2.2BookList类 3.user包 3.1User类 3.2NormalUser类 3.3AdminUser类 4.operation 4.1IOPeration接口 4.2ExitOperation类 4.3FindOperation类 4.4ShowOperation类 4.5AddOperation类 4.6DelOperation类 4.7BorrowOpera…...
C++ 函数模板与类模板
C最重要的特性之一就是代码重用,为了实现代码重用,代码必须具有通用性。通用代码应不受数据类型的影响,并且可以自动适应数据类型的变化。这种程序设计类型称为参数化程序设计。模板是C支持参数化程序设计的工具,通过它可以实现参…...

Tailwind CSS:简洁高效的工具,提升前端开发体验
112. Tailwind CSS:简洁高效的工具,提升前端开发体验 1. 什么是Tailwind CSS? Tailwind CSS是由Adam Wathan、Jonathan Reinink、David Hemphill和Steve Schoger等人共同创建的一种现代CSS框架。与传统的CSS框架不同,Tailwind CS…...
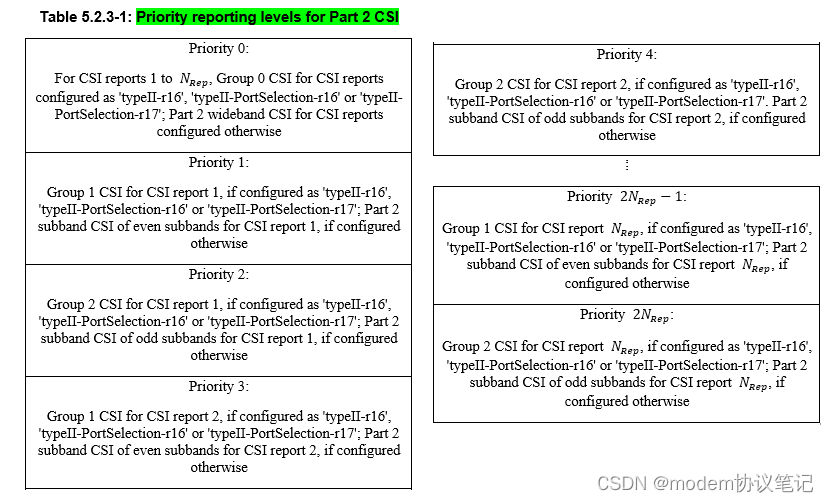
NR CSI(六) CSI reporting using PUCCH
之前NR CSI(二) the workflow of CSI report有对CSI report的相关流程进行介绍,而这篇主要看下CSI reporting over PUCCH的相关规定。 CSI report在PUCCH上传输的场景如上表红色字体,有三种场景,具体的对应的是Periodic 和Semi-Persistent CS…...
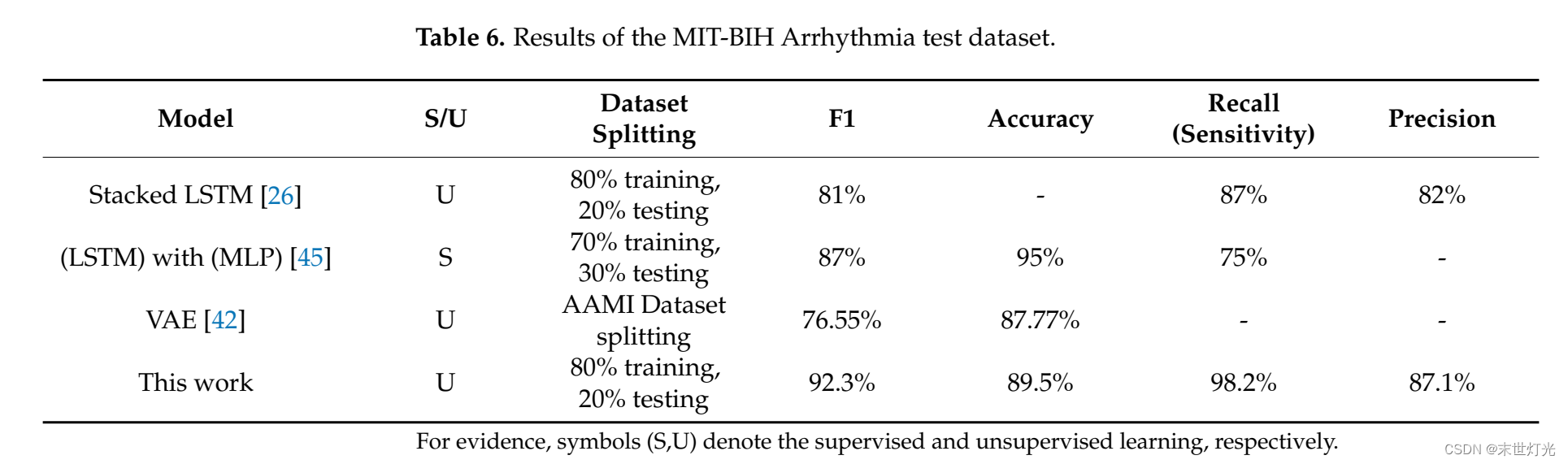
论文阅读---《Unsupervised Transformer-Based Anomaly Detection in ECG Signals》
题目:基于Transformer的无监督心电图(ECG)信号异常检测 摘要 异常检测是数据处理中的一个基本问题,它涉及到医疗感知数据中的不同问题。技术的进步使得收集大规模和高度变异的时间序列数据变得更加容易,然而ÿ…...

5G上行干扰规避的参数策略
LNR干扰避让 1. 干扰避让特性 D1/D2干扰避让:干扰与非干扰带宽独立测量,避免部分频带受干扰拉低整个带宽MCS,基于测量结果, 用户级自适应调度60/80/100M,躲避干扰频带。 窄带干扰避让:避免部分带宽的干扰对…...
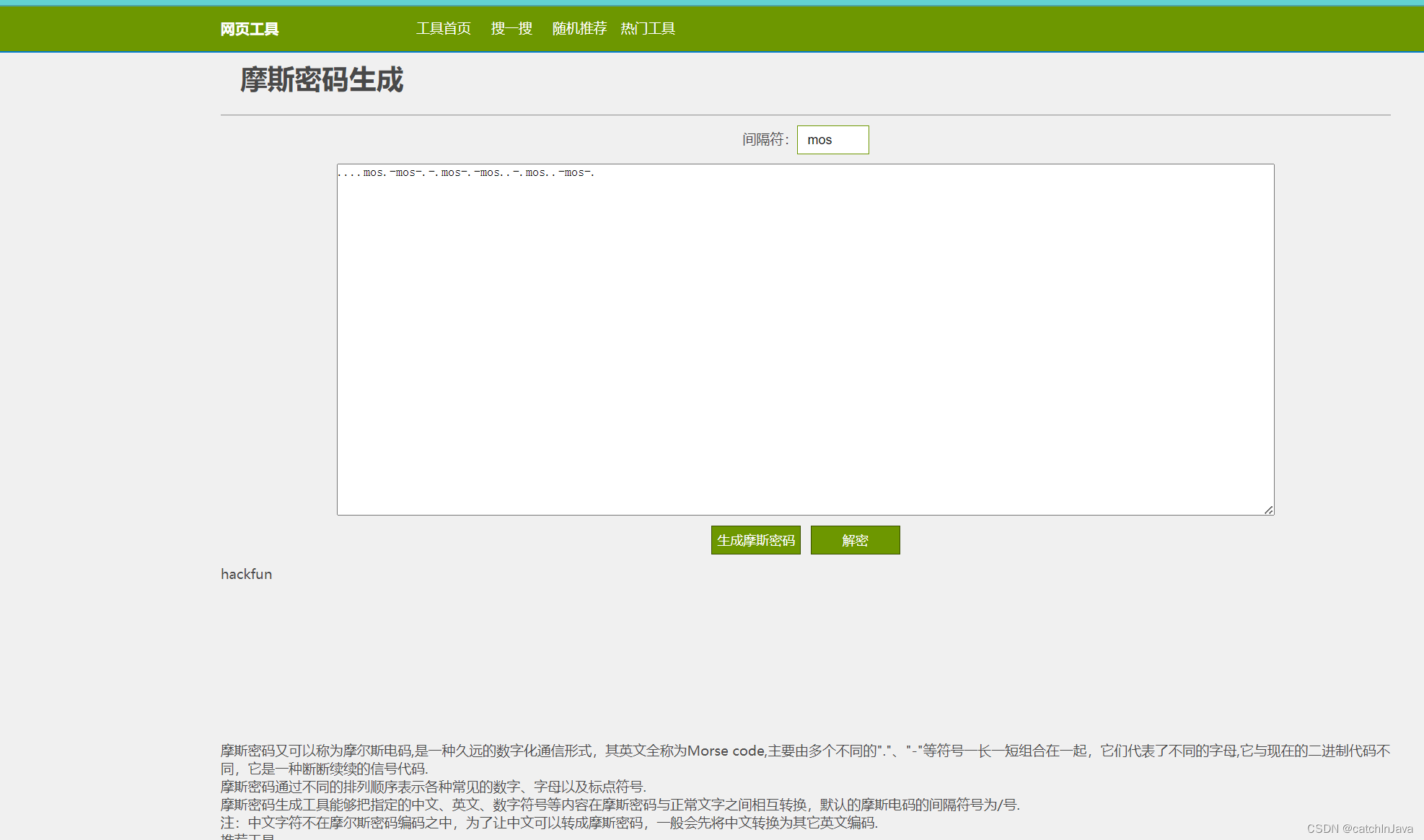
CTF流量题解tcp1
用流量工具进行分析。发现消息长度有点异常。右键TCP跟踪。 ....mos.-mos-.-.mos-.-mos..-.mos..-mos-. 摩斯密码生成-网页工具 (adminun.com)...
Django快速入门
文章目录 一、安装1.创建虚拟环境(virtualenv和virtualenvwrapper)2. 安装django 二、改解释器三、创建一个Django项目四、项目目录项目同名文件夹/settings.py 五、测试服务器启动六、数据迁移七、创建应用八、基本视图1. 返回响应 response2. 渲染模板…...

Python “牵手” 淘宝商品详情数据获取方法,淘宝API申请指南
淘宝详情接口 API 是淘宝开放平台提供的一种 API 接口,它可以帮助开发者获取淘宝商品的详细信息,包括商品的标题、描述、图片等信息。在淘宝电商平台的开发中,淘宝详情接口 API 是非常常用的 API,因此本文将详细介绍淘宝详情接口 …...

OpenScene
paper:OpenScene: 3D Scene Understanding with Open Vocabularies code: https://github.com/pengsongyou/openscene 摘要:传统的3D场景理解方法依赖于带标签的3D数据集,在有监督的情况下为单个任务训练模型。我们提出了OpenScene,一种替代性的方法,模型预测CLIP特征空…...
HDFS中的Trash垃圾桶回收机制
Trash垃圾桶回收机制 文件系统垃圾桶背景功能概述Trash Checkpoint Trash功能开启关闭HDFS集群修改core-site.xml删除文件到trash删除文件跳过从trash中恢复文件清空trash 文件系统垃圾桶背景 回收站(垃圾桶)是windows操作系统里的一个系统文件夹&#…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
