DIDL5_数值稳定性和模型初始化
数值稳定性和模型初始化
- 数值稳定性
- 梯度不稳定的影响
- 推导
- 什么是梯度消失?
- 什么是梯度爆炸?
- 如何解决数值不稳定问题?——参数初始化
- 参数初始化的几种方法
- 默认初始化
- Xavier初始化
- 小结
当神经网络变得很深的时候,数值特别容易不稳定。
我们实现的每个模型都是根据某个预先指定的分布来初始化模型的参数。
初始化方案的选择在神经网络学习中起着举足轻重的作用, 它对保持数值稳定性至关重要
数值稳定性
梯度不稳定的影响
糟糕初始化参数可能会导致我们在训练时遇到梯度爆炸或梯度消失。
不稳定梯度带来的风险不止在于数值表示; 不稳定梯度也威胁到我们优化算法的稳定性。
- 梯度爆炸(gradient exploding)问题: 参数更新过大,破坏了模型的稳定收敛;
- 梯度消失(gradient vanishing)问题: 参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。
推导
考虑一个具有LLL层、输入xxx和输出ooo的深层网络。每一层lll由变换flf_lfl定义, 该变换的参数为权重W(l)W^{(l)}W(l), 其隐藏变量是h(l)h^{(l)}h(l)(令 h0=xh^{0} = xh0=x)。
该网络可以表示为:
h(l)=fl(h(l−1))因此 o=fL∘…∘f1(x).\mathbf{h}^{(l)} = f_l (\mathbf{h}^{(l-1)}) \text{ 因此 } \mathbf{o} = f_L \circ \ldots \circ f_1(\mathbf{x}).h(l)=fl(h(l−1)) 因此 o=fL∘…∘f1(x).
如果所有隐藏变量和输入都是向量, 我们可以将o\mathbf{o}o关于任何一组参数W(l)\mathbf{W}^{(l)}W(l)的梯度写为下式:
∂W(l)o=∂h(L−1)h(L)⏟M(L)=def⋅…⋅∂h(l)h(l+1)⏟M(l+1)=def∂W(l)h(l)⏟v(l)=def.\partial_{\mathbf{W}^{(l)}} \mathbf{o} = \underbrace{\partial_{\mathbf{h}^{(L-1)}} \mathbf{h}^{(L)}}_{ \mathbf{M}^{(L)} \stackrel{\mathrm{def}}{=}} \cdot \ldots \cdot \underbrace{\partial_{\mathbf{h}^{(l)}} \mathbf{h}^{(l+1)}}_{ \mathbf{M}^{(l+1)} \stackrel{\mathrm{def}}{=}} \underbrace{\partial_{\mathbf{W}^{(l)}} \mathbf{h}^{(l)}}_{ \mathbf{v}^{(l)} \stackrel{\mathrm{def}}{=}}.∂W(l)o=M(L)=def∂h(L−1)h(L)⋅…⋅M(l+1)=def∂h(l)h(l+1)v(l)=def∂W(l)h(l).
该梯度是L−lL-lL−l个矩阵 M(L)⋅…⋅M(l+1)\mathbf{M}^{(L)} \cdot \ldots \cdot \mathbf{M}^{(l+1)}M(L)⋅…⋅M(l+1)与梯度向量v(l)\mathbf{v}^{(l)}v(l)的乘积。
因此,我们容易受到数值下溢问题的影响. 当将太多的概率乘在一起时,这些问题经常会出现。
什么是梯度消失?
激活函数sigmoid函数,1/(1+exp(−x))1/(1 + \exp(-x))1/(1+exp(−x)),类似于阈值函数。 由于早期的人工神经网络受到生物神经网络的启发, 神经元要么完全激活要么完全不激活(就像生物神经元)的想法很有吸引力。 然而,它却是导致梯度消失问题的一个常见的原因:
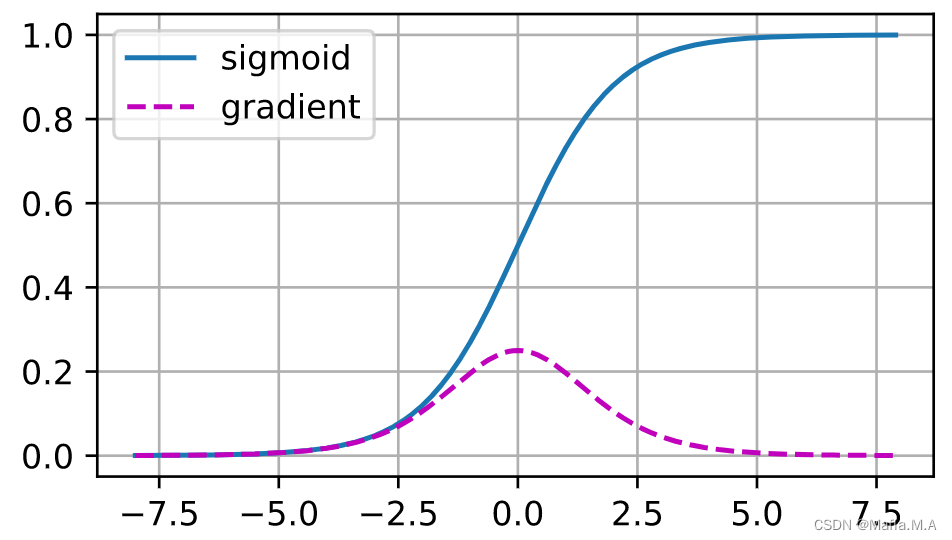
当sigmoid函数的输入很大或是很小时,它的梯度都会消失。当反向传播通过许多层时,除非我们在刚刚好的地方, 这些地方sigmoid函数的输入接近于零,否则整个乘积的梯度可能会消失。
当我们的网络有很多层时,除非我们很小心,否则在某一层可能会切断梯度。
更稳定的ReLU系列函数已经成为从业者的默认选择。
什么是梯度爆炸?
矩阵乘积发生了爆炸,这种情况是由于深度网络的初始化导致的,没有机会让梯度下降优化器收敛。
#pytorch
M = torch.normal(0, 1, size=(4,4))
print('一个矩阵 \n',M)
for i in range(100):M = torch.mm(M,torch.normal(0, 1, size=(4, 4)))print('乘以100个矩阵后\n', M)

如何解决数值不稳定问题?——参数初始化
参数初始化是解决(或至少减轻)上述问题的一种方法, 优化期间的注意和适当的正则化也可以进一步提高稳定性。
参数初始化的几种方法
默认初始化
如果我们不指定初始化方法, 框架将使用默认的随机初始化方法,对于中等难度的问题,这种方法通常很有效。
Xavier初始化
某些没有非线性的全连接层输出(例如,隐藏变量)oio_{i}oi的尺度分布。 对于该层ninn_\mathrm{in}nin输入xjx_jxj及其相关权重wijw_{ij}wij,输出由下式给出
oi=∑j=1ninwijxj.o_{i} = \sum_{j=1}^{n_\mathrm{in}} w_{ij} x_j.oi=j=1∑ninwijxj.
现在标准且实用的Xavier初始化的基础, 它以其提出者 (Glorot and Bengio, 2010) 第一作者的名字命名。 通常,Xavier初始化从均值为零,方差σ2=2nin+nout\sigma^2 = \frac{2}{n_\mathrm{in} + n_\mathrm{out}}σ2=nin+nout2的高斯分布中采样权重。 我们也可以将其改为选择从均匀分布中抽取权重时的方差。 注意均匀分布U(−a,a)U(-a, a)U(−a,a)的方差为a23\frac{a^2}{3}3a2。 将a23\frac{a^2}{3}3a2代入到σ2\sigma^2σ2的条件中,将得到初始化值域:
U(−6nin+nout,6nin+nout).U\left(-\sqrt{\frac{6}{n_\mathrm{in} + n_\mathrm{out}}}, \sqrt{\frac{6}{n_\mathrm{in} + n_\mathrm{out}}}\right).U(−nin+nout6,nin+nout6).
尽管在上述数学推理中,“不存在非线性”的假设在神经网络中很容易被违反, 但Xavier初始化方法在实践中被证明是有效的。
小结
- 梯度消失和梯度爆炸是深度网络中常见的问题。在参数初始化时需要非常小心,以确保梯度和参数可以得到很好的控制。
- 需要用启发式的初始化方法来确保初始梯度既不太大也不太小。
- ReLU激活函数缓解了梯度消失问题,这样可以加速收敛。
- 随机初始化是保证在进行优化前打破对称性的关键。
- Xavier初始化表明,对于每一层,输出的方差不受输入数量的影响,任何梯度的方差不受输出数量的影响。
相关文章:

DIDL5_数值稳定性和模型初始化
数值稳定性和模型初始化数值稳定性梯度不稳定的影响推导什么是梯度消失?什么是梯度爆炸?如何解决数值不稳定问题?——参数初始化参数初始化的几种方法默认初始化Xavier初始化小结当神经网络变得很深的时候,数值特别容易不稳定。我…...

火狐浏览器推拽开新的窗口
今天我测试的时候,发现我拖拽一下火狐会打开了新的窗口,谷歌就不会,所以我们要阻止一下默认行为const disableFirefoxDefaultDrop () > {const isFirefox navigator.userAgent.toLowerCase().indexOf(firefox) ! -1if (isFirefox) {docu…...

vrrp+mstp+osfp经典部署案例
LSW1和LSW2和LSW3和LSW4上面启用vrrpmstp组网: vlan 10 全走LSW1出再走AR2到外网,vlan 20 全走LSW2出再走AR3到外网 配置注意:mstp实例的根桥在哪,vrrp的主设备就是谁 ar2和ar3上开nat ar2和ar3可以考虑换成两台防火墙来做&…...
AI_News周刊:第二期
2023.02.13—2023.02.17 1.ChatGPT 登上TIME时代周刊封面 这一转变标志着自社交媒体以来最重要的技术突破。近几个月来,好奇、震惊的公众如饥似渴地采用了生成式人工智能工具,这要归功于诸如 ChatGPT 之类的程序,它对几乎任何查询做出连贯&a…...

【C++的OpenCV】第一课-opencv的间接和安装(Linux环境下)
第一课-目录一、基本介绍1.1 官网1.2 git源码1.3 介绍二、OpenCV的相关部署工作2.1 Linux平台下部署OpenCV一、基本介绍 1.1 官网 opencv官网 注意:官网为英文版本,可以使用浏览器自带的翻译插件进行翻译,真心不推荐大家去看别人翻译的&am…...

为什么建议使用你 LocalDateTime ,而不是 Date
为什么建议使用你 LocalDateTime ,而不是 Date? 在项目开发过程中经常遇到时间处理,但是你真的用对了吗,理解阿里巴巴开发手册中禁用static修饰SimpleDateFormat吗 通过阅读本篇文章你将了解到: 为什么需要LocalDate…...
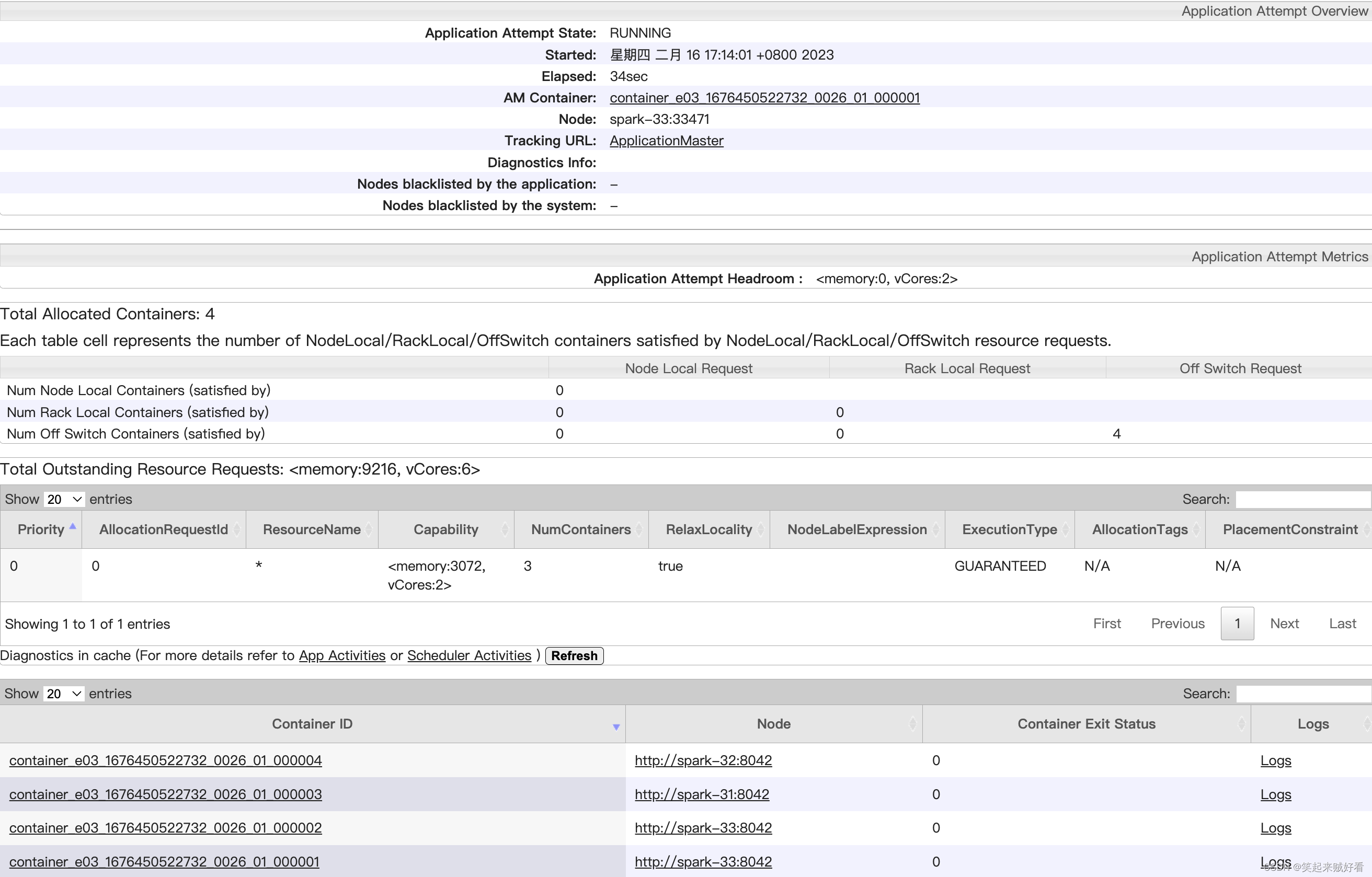
【大数据】HADOOP-YARN容量调度器Spark作业实战
目录需求配置多队列的容量调度器验证队列资源需求 default 队列占总内存的40%,最大资源容量占总资源的60% ops 队列占总内存的60%,最大资源容量占总资源的80% 配置多队列的容量调度器 在yarn-site.xml里面配置使用容量调度器 <!-- 使用容量调度器…...

平面及其方程
一、曲面和交线的定义 空间解析几何中,任何曲面或曲线都看作点的几何轨迹。在这样的意义下,如果曲面SSS与三元方程: F(x,y,z)0(1)F(x,y,z)0\tag{1} F(x,y,z)0(1) 有下述关系: 曲面 SSS 上任一点的坐标都满足方程(1)(1)(1)不在曲…...

7 配置的封装
概述 IPC设备通常有三种配置信息:一是默认配置,存储了设备所有配置项的默认值,默认配置是只读的,不能修改;二是用户配置,存储了用户修改过的所有配置项;三是私有配置,存储了程序内部使用的一些配置项,比如:固件升级的URL、固件升级标志位等。恢复出厂设置的操作,实际…...

03_Docker 入门
03_Docker 入门 文章目录03_Docker 入门3.1 确保 Docker 已经就绪3.2 运行我们的第一个容器3.3 使用第一个容器3.4 容器命名3.5 重新启动已经停止的容器3.6 附着到容器上3.7 创建守护式容器3.8 容器内部都在干些什么3.9 Docker 日志驱动3.10 查看容器内的进程3.11 Docker 统计信…...

Python 为什么要 if __name__ == “__main__“:
各位读者,你们知道以下两个Python文件有什么区别吗? main1.py def main():output Helloprint(output)if __name__ "__main__":main()main2.py output Hello print(output)当我们直接运行 main1.py 与 main2.py 的时候,程序都…...
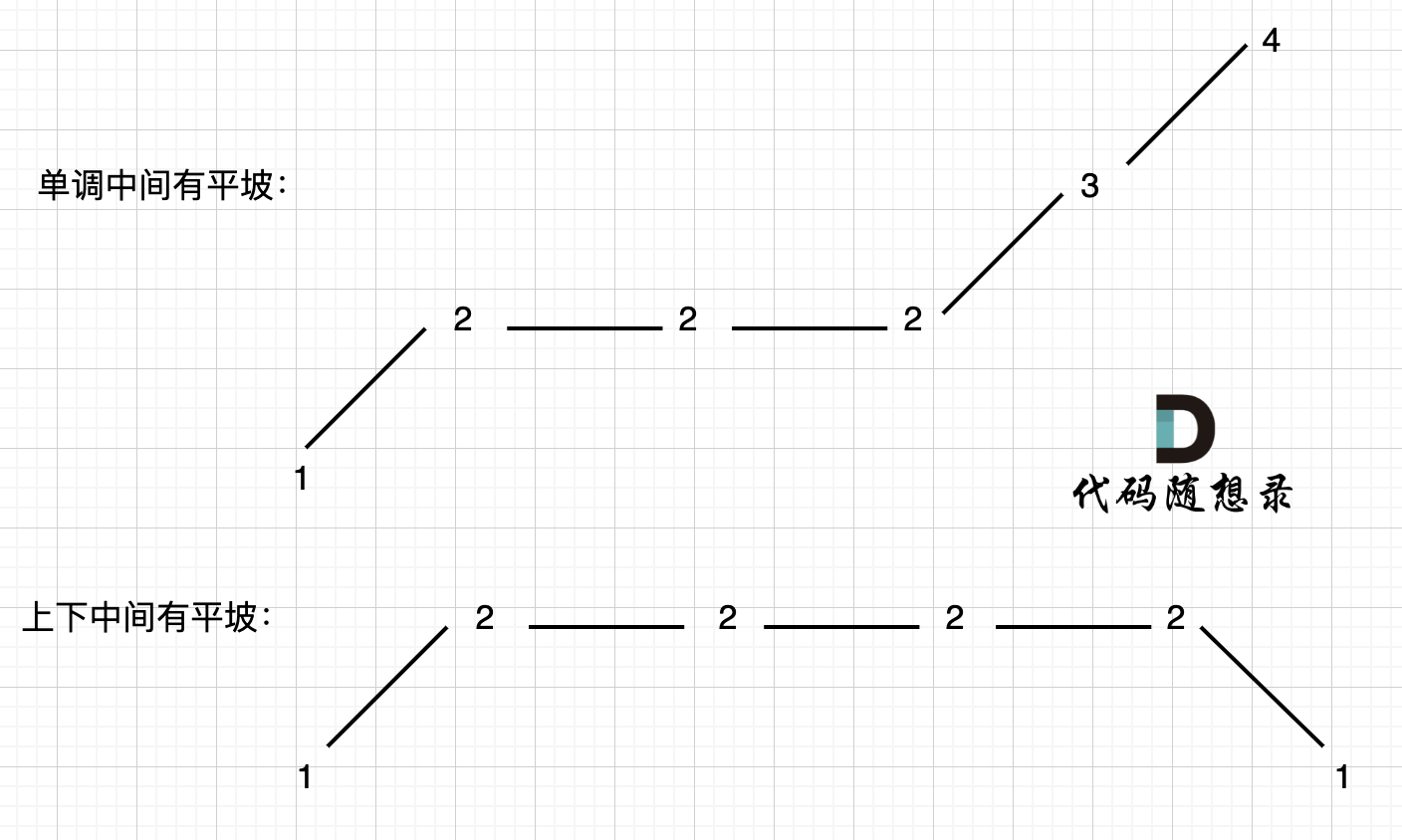
455. 分发饼干、376. 摆动序列、53. 最大子数组和
455.分发饼干 题目描述: 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块…...
基于Springbot+微信小程序的购药平台的设计与实现
基于Springbot微信小程序的购药平台的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、…...

aws lambda rust的sdk和自定义运行时
rust的aws sdk 参考资料 https://docs.aws.amazon.com/sdk-for-rust/latest/dg/getting-started.htmlhttps://awslabs.github.io/aws-sdk-rust/https://github.com/awslabs/aws-sdk-rusthttps://github.com/awsdocs/aws-doc-sdk-examples/tree/main/rust_dev_preview rus sd…...
[安装之3] 笔记本加装固态和内存条教程(超详细)
由于笔记本是几年前买的了,当时是4000,现在用起来感到卡顿,启动、运行速度特别慢,就决定换个固态硬盘,加个内存条,再给笔记本续命几年。先说一下加固态硬盘SSD的好处:1.启动快 2.读取延迟小 3.写…...

极客时间左耳听风-高效学习
左耳听风——高效学习篇 P95 | 高效学习:端正学习态度 本人真实⬇️⬇️⬇️⬇️ “ 大部分人都认为自己爱学习,但是: 他们都是只有意识没有行动,他们是动力不足的人。 他们都不知道自己该学什么,他们缺乏方向和目标。…...

MSR寄存器访问
1.介绍 MSR是CPU的一组64位寄存器,每个MSR都有它的地址值(如下图所示),可以分别通过RDMSR 和WRMSR 两条指令进行读和写的操作。 如图中为8个P-state寄存器,地址分别为0xC001 0064 ~ 0xC001 006B,每个寄存…...
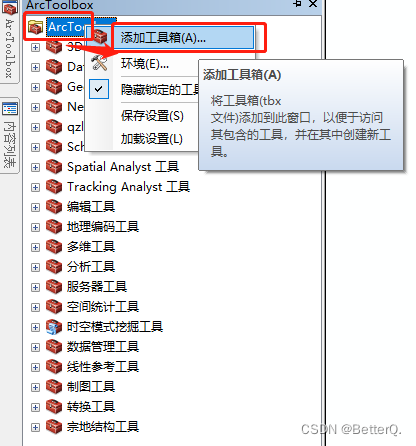
ArcGIS:模型构建器实现批量按掩膜提取影像
用研究区域的矢量数据来裁剪栅格数据集时,一般我们使用ArcGIS中的【按掩膜提取工具】。如果需要裁剪的栅格数据太多,处理起来非常的麻烦,虽然ArcGIS中有批处理的功能,但是还是需要手动选择输入输出数据。 如下图,鼠标…...

算法刷题打卡第94天: 找出给定方程的正整数解
找出给定方程的正整数解 难度:中等 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调…...
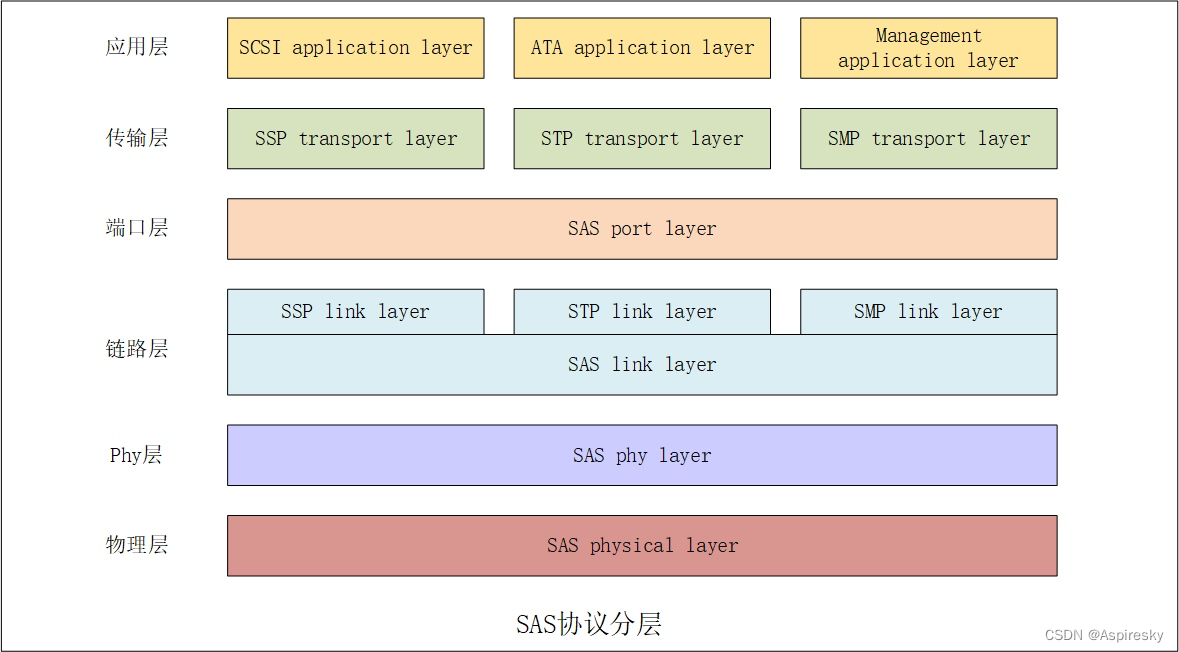
浅析SAS协议(1):基本介绍
文章目录概述SAS协议发展历程SAS技术特性SAS设备拓扑SAS phySAS地址SAS设备类型SAS协议分层参考链接概述 SAS,全称Serial Attached SCSI,即串行连结SCSI,是一种采用了串行总线的高速互连技术。通过物理上使用串行总线连结,在链路…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
