时间复杂度与空间复杂度的详解
目录
1.时间复杂度
2.时间复杂度计算例题
3.空间复杂度
1.时间复杂度
算法中的基本操作的执行次数,为算法的时间复杂度。
1、用常数1取代运行时间中的所有加法常数。2、在修改后的运行次数函数中,只保留最高阶项。3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
举例:
// 请计算一下 func1 基本操作执行了多少次?void func1 ( int N ){int count = 0 ;for ( int i = 0 ; i < N ; i ++ ) {for ( int j = 0 ; j < N ; j ++ ) {count ++ ;}}for ( int k = 0 ; k < 2 * N ; k ++ ) {count ++ ;}int M = 10 ;while (( M -- ) > 0 ) {count ++ ;}System . out . println ( count );}
题解:
Func1 执行的基本操作次数 :F(N)=N^2+2*N+10;(1) 用常数1取代运行时间中的所有加法常数。F(N)=N^2+2*N+1;(2) 在修改后的运行次数函数中,只保留最高阶项。F(N)=N^2;=>O(N^2);
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
最坏情况:任意输入规模的最大运行次数 ( 上界 )平均情况:任意输入规模的期望运行次数最好情况:任意输入规模的最小运行次数 ( 下界 )
2.时间复杂度计算例题
例题1:
// 计算 func2 的时间复杂度?void func2 ( int N , int M ) {int count = 0 ;for ( int k = 0 ; k < M ; k ++ ) {count ++ ;}for ( int k = 0 ; k < N ; k ++ ) {count ++ ;}System . out . println ( count );}
答案及分析:
基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
例题2:
// 计算 func3 的时间复杂度?void func3 ( int N ) {int count = 0 ;for ( int k = 0 ; k < 100 ; k ++ ) {count ++ ;}System . out . println ( count );}
答案及分析:
基本操作执行了100次,通过推导大O阶方法,时间复杂度为 O(1)
例题3:
// 计算 bubbleSort 的时间复杂度?void bubbleSort ( int [] array ) {for ( int end = array . length ; end > 0 ; end -- ) {boolean sorted = true ;for ( int i = 1 ; i < end ; i ++ ) {if ( array [ i - 1 ] > array [ i ]) {Swap ( array , i - 1 , i );sorted = false ;}}if ( sorted == true ) {break ;}}}
答案及分析:
O(N)中N表示问题的规模

F(N)=N*(N-1)=N^2-N;
例题4:
// 计算 binarySearch 的时间复杂度?int binarySearch ( int [] array , int value ) {int begin = 0 ;int end = array . length - 1 ;while ( begin <= end ) {int mid = begin + (( end - begin ) / 2 );if ( array [ mid ] < value )begin = mid + 1 ;else if ( array [ mid ] > value )end = mid - 1 ;elsereturn mid ;}return - 1 ;}
答案及分析:
方法1:
对于不能直接看出的并较复杂的问题,可以采用数学归纳法
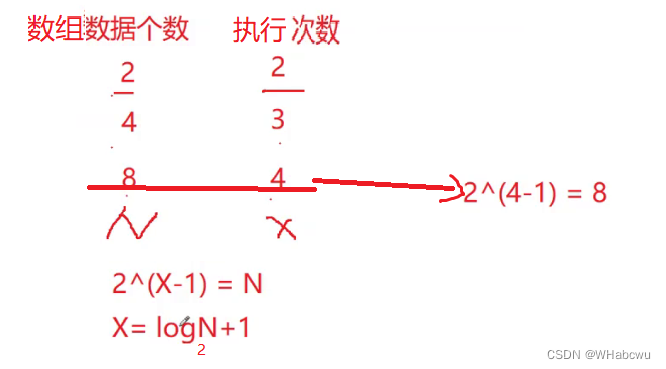
答案:
方法2:

N/(2^x) =1(x为循环的执行次数)
x的解:

例题 5
// 计算阶乘递归 factorial 的时间复杂度?long factorial ( int N ) {return N < 2 ? N : factorial ( N - 1 ) * N ;}
对于不能直接看出的并较复杂的问题,可以采用数学归纳法,但对于递归我们有专门总结的方法。
F(N)=递归的次数*每次递归代码的执行次数
答案及分析:
通过计算分析发现基本操作递归了 N次, 每次递归代码的执行次数为1 时间复杂度为O(N)
例题6:
// 计算斐波那契递归 fifibonacci 的时间复杂度?int fifibonacci ( int N ) {return N < 2 ? N : fifibonacci ( N - 1 ) + fifibonacci ( N - 2 );}
答案及分析:
对于不能直接看出的并较复杂的问题,可以采用数学归纳法(不展开)
面对这种多递归入口的题,可以使用补全法。
何为补全法?
以F4为例
F(N):
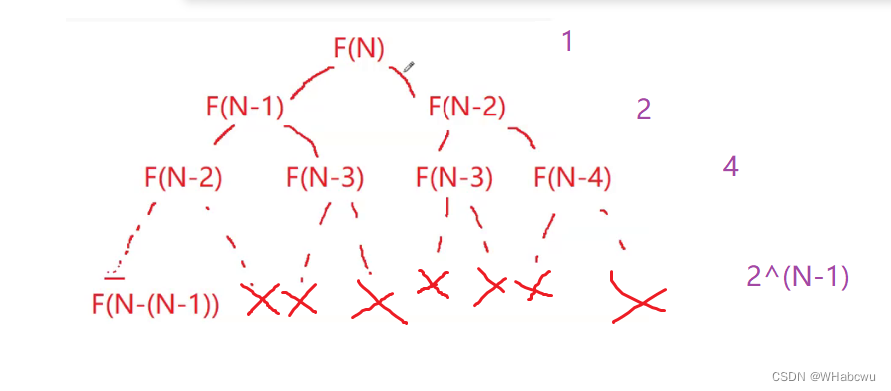
3.空间复杂度
空间复杂度是对一个算法在运行过程中 临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少 bytes 的空 间,因为这个也没太大意义,所以空间复杂度算的是变量的个数
例题1:
// 计算 bubbleSort 的空间复杂度?void bubbleSort ( int [] array ) {for ( int end = array . length ; end > 0 ; end -- ) {boolean sorted = true ;for ( int i = 1 ; i < end ; i ++ ) {if ( array [ i - 1 ] > array [ i ]) {Swap ( array , i - 1 , i );sorted = false ;}}if ( sorted == true ) {break ;}}}
答案及分析:

使用了常数个额外空间,所以空间复杂度为 O(1)
例题2:
// 计算 fifibonacci 的空间复杂度?int [] fifibonacci ( int n ) {long [] fifibArray = new long [ n + 1 ];fifibArray [ 0 ] = 0 ;fifibArray [ 1 ] = 1 ;for ( int i = 2 ; i <= n ; i ++ ) {fifibArray [ i ] = fifibArray [ i - 1 ] + fifibArray [ i - 2 ];}return fifibArray ;}
答案及分析:
动态开辟了N个空间,空间复杂度为 O(N)
例题3:
// 计算阶乘递归 Factorial 的空间复杂度?long factorial ( int N ) {return N < 2 ? N : factorial ( N - 1 ) * N ;}
答案及分析:
递归调用了 N 次,开辟了 N 个栈帧,每个栈帧使用了常数个空间。空间复杂度为 O(N)
以上为我个人的小分享,如有问题,欢迎讨论!!!
都看到这了,不如关注一下,给个免费的赞 ![]()

相关文章:

时间复杂度与空间复杂度的详解
目录 1.时间复杂度 2.时间复杂度计算例题 3.空间复杂度 1.时间复杂度 算法中的基本操作的执行次数,为算法的时间复杂度。 如何表达 时间复杂度? 大O的渐进表示法 实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数…...
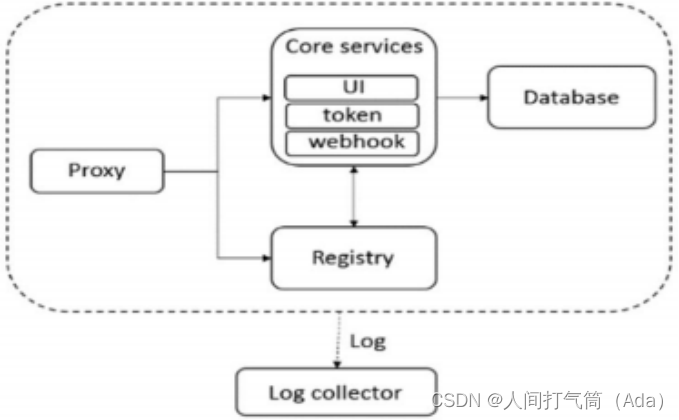
每日一学:什么是 Harbor ?
目录 什么是 Harbor ? 一、Harbor 的优势 二、Harbor 架构构成 三、Core services 这是 Harbor 的核心功能 什么是 Harbor ? Harbor 是 VMware 公司开源的企业级 Docker Registry 项目,其目标是帮助用户迅速搭建一个企业级的 Docker Reg…...
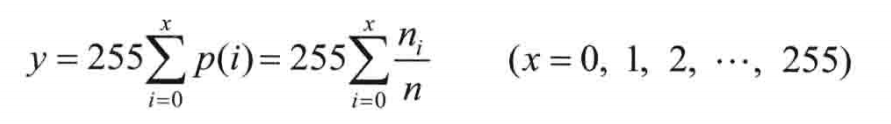
灰度均衡变换之c++实现(qt + 不调包)
1.基本原理 灰度均衡是以累计分布函数变换为基础的直方图修正法,它可以产生一副灰度级分布概率均匀的图像。也就是说,经过灰度均衡后的图像在没一级灰度上像素点的数量相差不大。公式见下图,为灰度值为x的像素点的个数,n为总像素点…...

flink1.17 自定义trigger ContinuousEventTimeTrigger
在 ContinuousEventTimeTrigger 的基础上新增了timeout,如果超时后窗口都没关闭,那么就硬输出一波,避免间断数据,留存窗口太久. ContinuousEventTimeTrigger ContinuousEventTimeTrigger连续事件时间触发器与ContinuousProcessingTimeTrigger连续处理时间触发器,指定一个固定…...

AIGC:【LLM(五)】——Faiss:高效的大规模相似度检索库
文章目录 一.简介1.1 什么是Faiss1.2 Faiss的安装 二.Faiss检索流程2.1 构建向量库2.2 构建索引2.3 top-k检索 三.Faiss构建索引的多种方式3.1 Flat :暴力检索3.2 IVFx Flat :倒排暴力检索3.3 IVFxPQy 倒排乘积量化3.4 LSH 局部敏感哈希3.5 HNSWx 一.简介…...
-[记忆的类型Ⅱ])
自然语言处理从入门到应用——LangChain:记忆(Memory)-[记忆的类型Ⅱ]
分类目录:《自然语言处理从入门到应用》总目录 对话知识图谱记忆(Conversation Knowledge Graph Memory) 这种类型的记忆使用知识图谱来重建记忆: from langchain.memory import ConversationKGMemory from langchain.llms impo…...

桥接模式-java实现
桥接模式 桥接模式的本质,是解决一个基类,存在多个扩展维度的的问题。 比如一个图形基类,从颜色方面扩展和从形状上扩展,我们都需要这两个维度进行扩展,这就意味着,我们需要创建一个图形子类的同时&#x…...

Linux systemd管理常用的几个小案例
systemd是目前Linux系统上主要的系统守护进程管理工具,配置文件要以.service结尾且放到 /usr/lib/systemd/system/目录下面 1、systemd管理ElasticSearch [Unit] DescriptionElasticsearch Service[Service] Typeforking Userelastic Groupelastic ExecStart/home…...
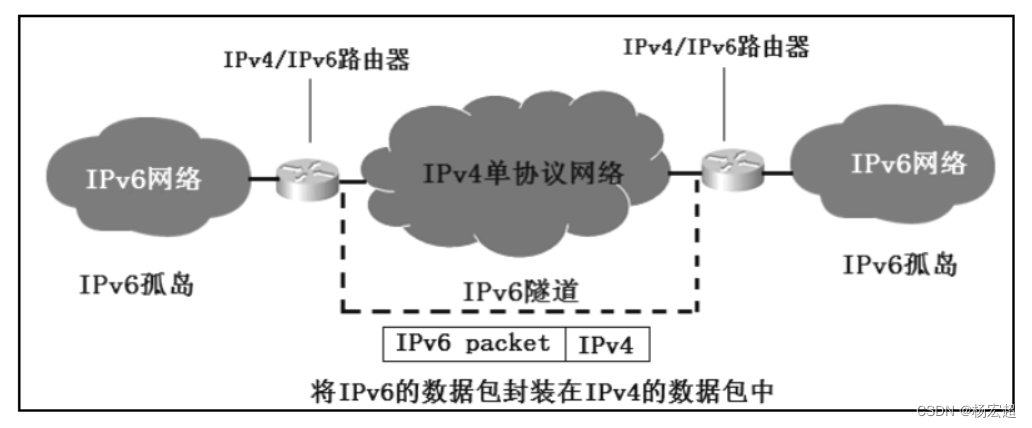
38、IPv6过渡技术
本节内容作为IPv6相关知识的最后一节内容,同时也作为我们本专栏网络层知识的最后一节内容,主要介绍从IPv4地址到IPv6地址过渡的相关技术。在这里我们只学习各类考试中常考的三种技术。 IPv4向IPv6的过渡 在前面的知识中,我们学习到了两种IP地…...

HMMER-序列分析软件介绍
HMMER是一个软件包,它提供了制作蛋白质和DNA序列域家族概率模型的工具,称为轮廓隐马尔可夫模型、轮廓HMM或仅轮廓,并使用这些轮廓来注释新序列、搜索序列数据库以寻找其他同源物,以及进行深度多重序列比对。HMMER是已知蛋白质和DN…...
【项目学习1】如何将java对象转化为XML字符串
如何将java对象转化为XML字符串 将java对象转化为XML字符串,可以使用Java的XML操作库JAXB,具体操作步骤如下: 主要分为以下几步: 1、创建JAXBContext对象,用于映射Java类和XML。 JAXBContext jaxbContext JAXBConte…...

nginx负载均衡
负载均衡:反向代理来实现 正向代理的配置方法。 1、NGINX的七层代理和四层代理: 七层是最常用的反向代理方式,只能配置在nginx配置文件的http模块。而且配置方法名称:upstream 模块,不能写在server中,也…...
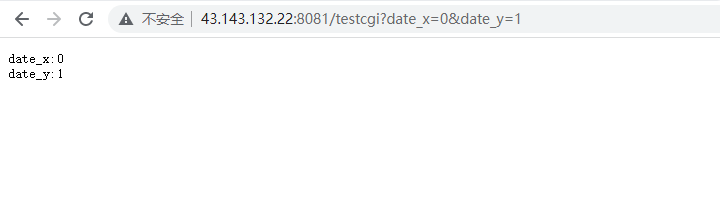
【毕业项目】自主设计HTTP
博客介绍:运用之前学过的各种知识 自己独立做出一个HTTP服务器 自主设计WEB服务器 背景目标描述技术特点项目定位开发环境WWW介绍 网络协议栈介绍网络协议栈整体网络协议栈细节与http相关的重要协议 HTTP背景知识补充特点uri & url & urn网址url HTTP请求和…...
关于安卓jar包修改并且重新发布
背景: 对于某些jar包,其内部是存在bug的,解决的方法无外乎就有以下几种方法: (1)通过反射,修改其赋值逻辑 (2)通过继承,重写其方法 (3࿰…...

Java课题笔记~ AspectJ 对 AOP 的实现(掌握)
AspectJ 对 AOP 的实现(掌握) 对于 AOP 这种编程思想,很多框架都进行了实现。Spring 就是其中之一,可以完成面向切面编程。然而,AspectJ 也实现了 AOP 的功能,且其实现方式更为简捷,使用更为方便,而且还支…...
npm 报错 cb() never called!
不知道有没有跟我一样的情况,在使用npm i的时候一直报错:cb() never called! 换了很多个node版本,还是不行,无法解决这个问题 百度也只是让降低node版本请缓存,gpt给出的解决方案也是同样的 但是缓存清过很多次了&a…...

finally有什么作用以及常用场景
在Java中,finally是一个关键字,用于定义一个代码块,该代码块中的代码无论是否发生异常都会被执行。finally块通常用于确保在程序执行过程中资源的释放和清理。 使用场景: 1. 资源释放:finally块经常用于释放打开的资…...

Python web实战之Django URL路由详解
概要 技术栈:Python、Django、Web开发、URL路由 Django是一种流行的Web应用程序框架,它采用了与其他主流框架类似的URL路由机制。URL路由是指将传入的URL请求映射到相应的视图函数或处理程序的过程。 什么是URL路由? URL路由是Web开发中非常…...
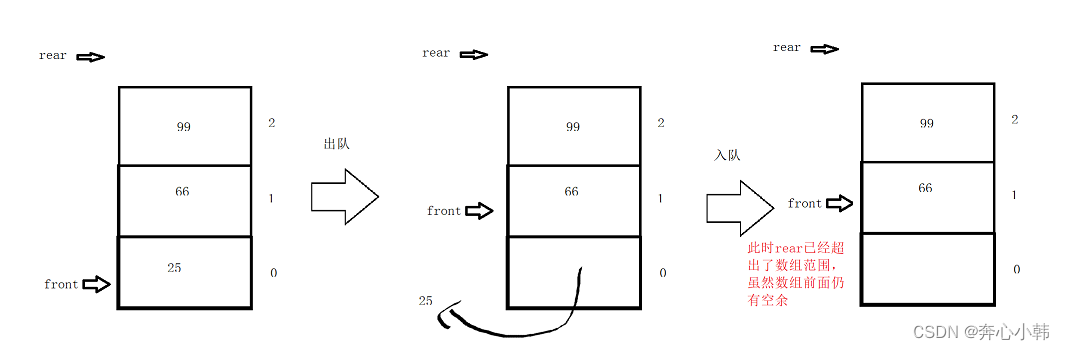
10-数据结构-队列(C语言)
队列 目录 目录 队列 一、队列基础知识 二、队列的基本操作 1.顺序存储 编辑 (1)顺序存储 (2)初始化及队空队满 (3)入队 (4)出队 (5)打印队列 &…...

面试之快速学习C++11 - 右值 移动构造 std::move
C11右值引用 字面意思,以引用传递的方式使用c右值左值和右值,左值是lvalue loactor value 存储在内存中,有明确存储地址的数据, 右值rvalue read value , 指的是那些可以提供数据值的数据(不一定可以寻址,…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
