自抗扰控制ADRC之微分器TD
目录
前言
1 全程快速微分器
1.1仿真分析
1.2仿真模型
1.3仿真结果
1.4结论
2 Levant微分器
2.1仿真分析
2.2仿真模型
2.3仿真结果
3.总结
前言
工程上信号的微分是难以得到的,所以本文采用微分器实现带有噪声的信号及其微分信号提取,从而实现无需测量速度信号的控制。并且结合控制对象简单的用PID进行控制,即TD微分器+PID控制。
1 全程快速微分器
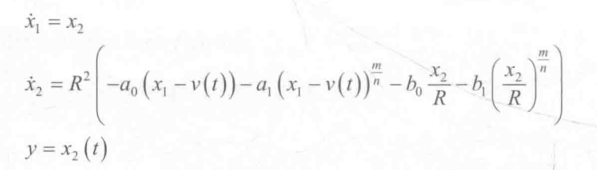
其中:
①x1为带有噪音的信号,也是TD的第一个状态变量,同理x2为信号的微分;
②R>0;a0、a1、b0、b1≥0;m和n为大于0的奇数,且m<n;
③当a1=b1=0时,上述微分器为线性微分器。
1.1仿真分析
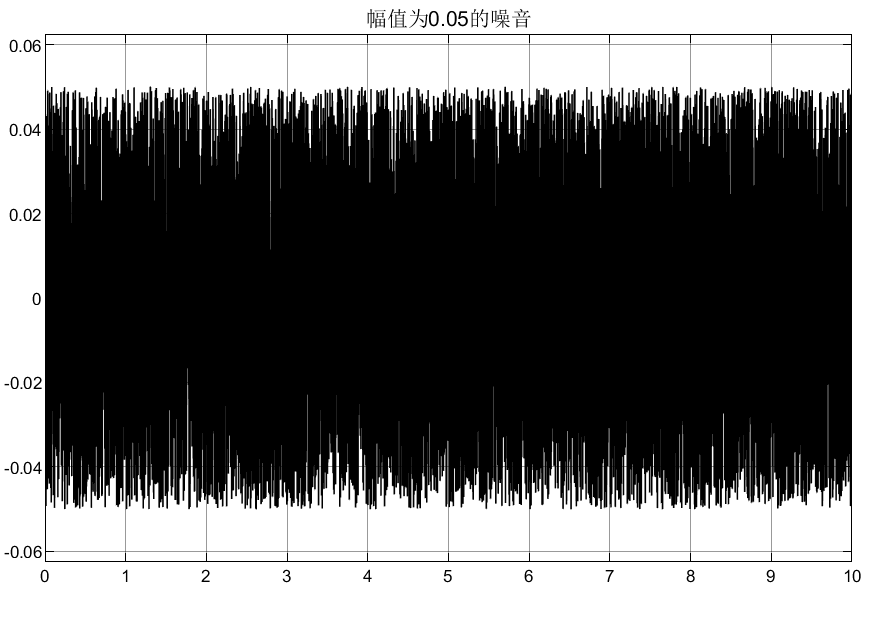
取R=1/0.05, a=0.1,b=0.1,已知输入信号为v(t)= sint,并且带有噪声信号,噪声的幅值为0.05,采用连续的全程快速微分器提取信号及信号的微分。
1.2仿真模型

1.3仿真结果
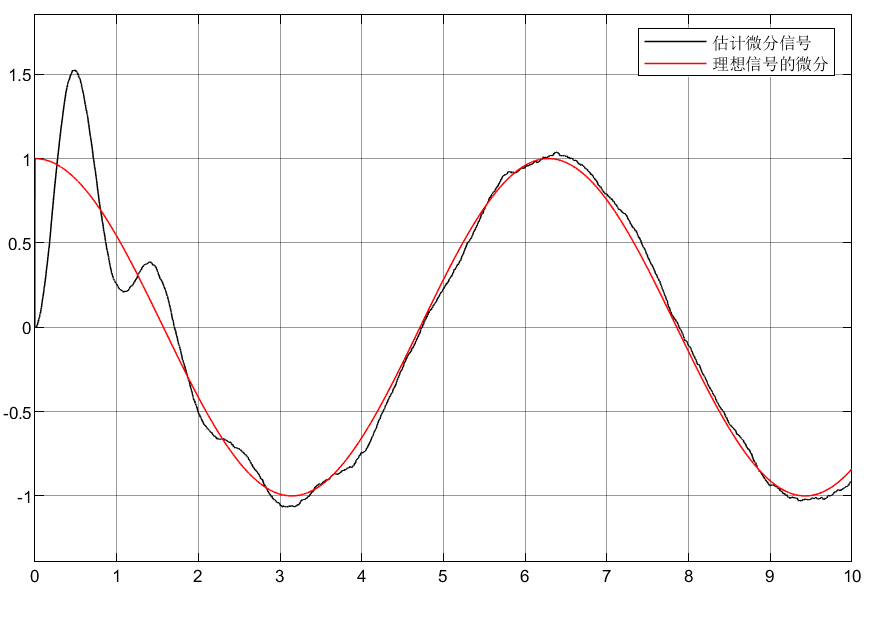
1.4结论
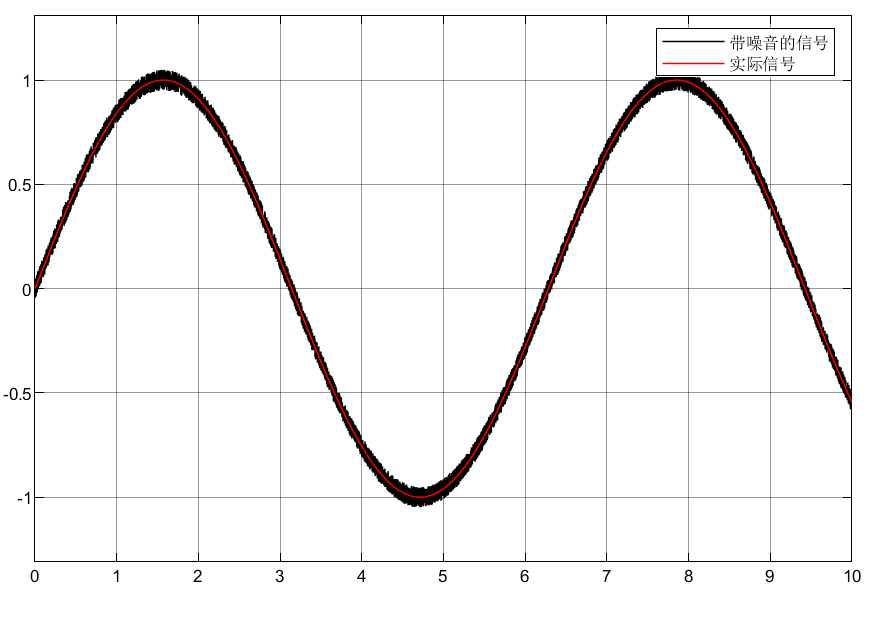
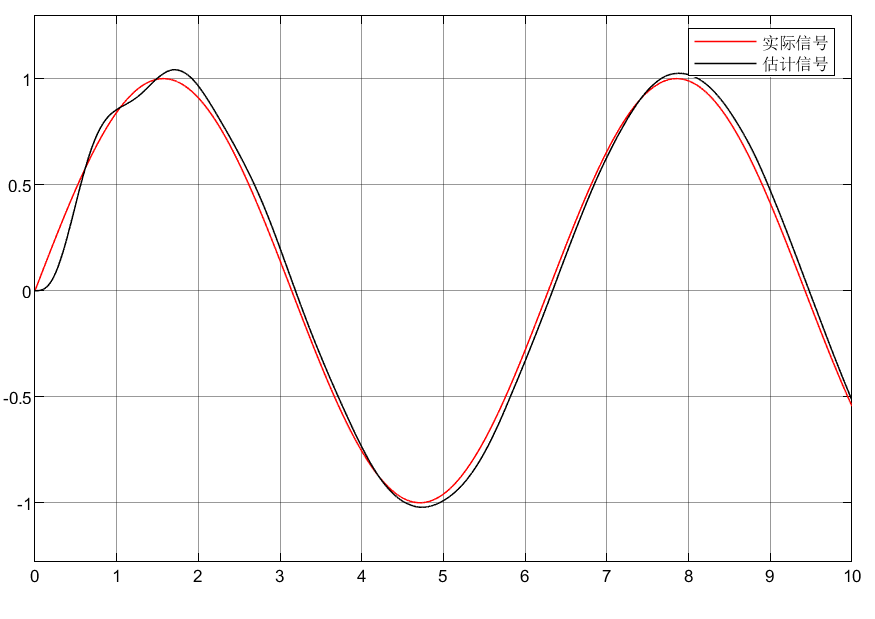
①可以看到虽然和实际信息有些偏差,但是估计的效果还算可以。
②对于a1、b1≠0的非线性微分器好像调节效果和线性差不多,即a1、b1、m、n调节没效果?
③位移信号可以调节的很好,但是会牺牲微分信号。
④仿真注意:(1)噪声模块的采样时间为继承采样时间;(2)simulink仿真求解步长为定步长0.001
2 Levant微分器
微分器需要对信号的测量误差和输入噪声具有鲁棒性,而Levant微分器是基于滑模奇数的非线性微分器,其二阶微分器表达形式为:
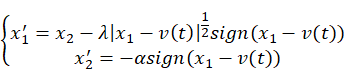

对于Lipschitz的定义部分可参考下面博客的3.1部分:
基于LMI的非线性混沌系统滑模控制_Mr. 邹的博客-CSDN博客
注:虽然这类微分器具有滑模控制的鲁棒性,但是对于Levant微分器,需要事先知道输入信号v(t)导数的Lipschitz常数上界,才能设计微分器参数,这就限制了输入信号的类型。而且,对于这种微分器,抖振现象不可避免。
2.1仿真分析
同样取上述的噪音信号及其微分进行估计,选取参数:
①Lipschitz的常数上界为1,即C = 1,所以α > 1,取α = 18;
②λ > 4*C*(α+C)/(α-C),得λ≥4.4706,所以取λ = 6。
2.2仿真模型
2.3仿真结果
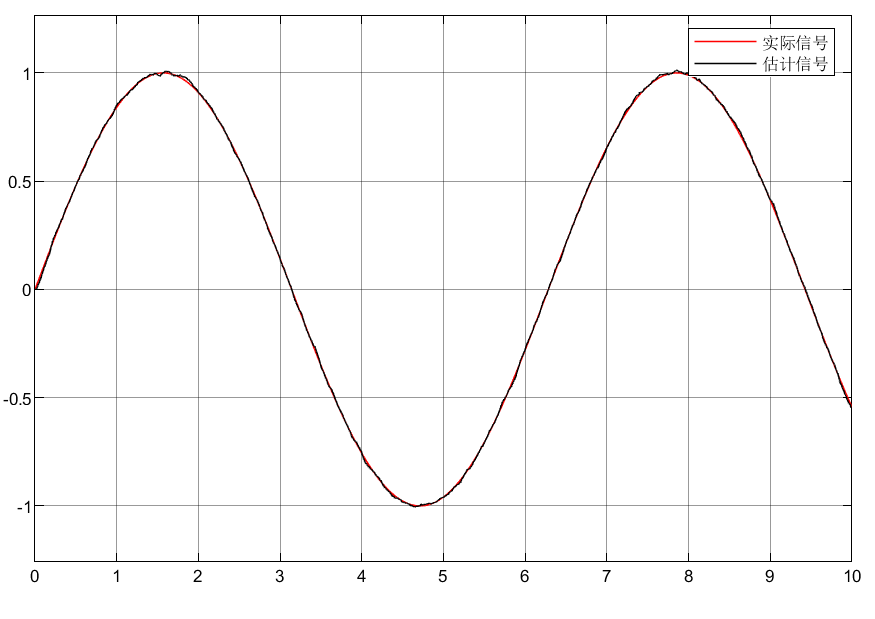
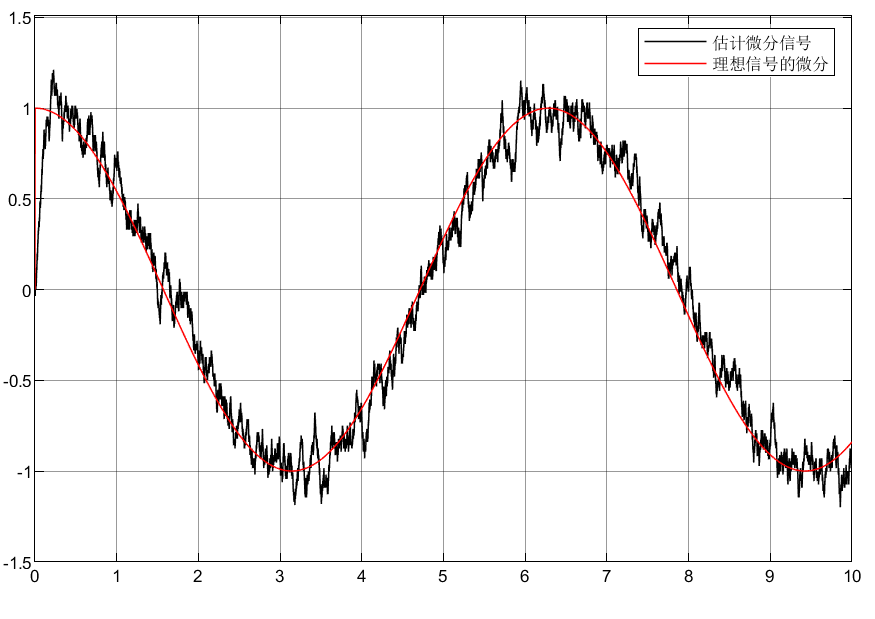
3.总结
①可以看到两种微分器都能将实现带噪声信号的估计,虽然有一定的误差
②信号的微分估计的稍差一些
③注意仿真时噪声模块的采样时间设定为继承采样时间:-1;且simulink设定为定步长0.001的求解器。
相关文章:

自抗扰控制ADRC之微分器TD
目录 前言 1 全程快速微分器 1.1仿真分析 1.2仿真模型 1.3仿真结果 1.4结论 2 Levant微分器 2.1仿真分析 2.2仿真模型 2.3仿真结果 3.总结 前言 工程上信号的微分是难以得到的,所以本文采用微分器实现带有噪声的信号及其微分信号提取,从而实现…...

链表学习之复制含随机指针的链表
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 复制含随机指针的链表 该链表节点的结构如下: class ListRandomNode { public:ListRandomNode() : val(0), next(nullptr), random(nullptr…...
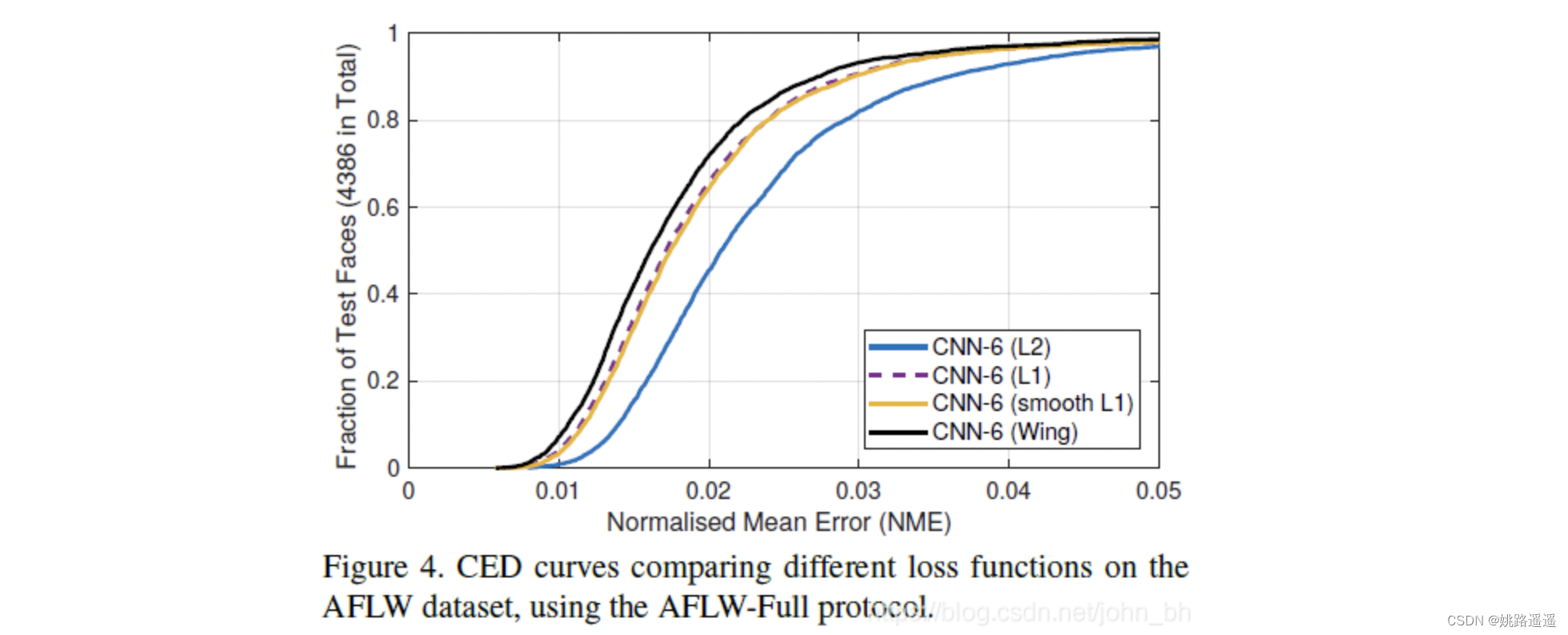
【人脸检测】Yolov5Face:优秀的one-stage人脸检测算法
论文题目:《YOLO5Face: Why Reinventing a Face Detector》 论文地址:https://arxiv.org/pdf/2105.12931.pdf 代码地址:https://github.com/deepcam-cn/yolov5-face 1.简介 近年来,CNN在人脸检测方面已经得到广泛的应用。但是许多…...
【Unity3d】Unity与Android之间通信
在unity开发或者sdk开发经常遇到unity与移动端原生层之间进行通信,这里把它们之间通信做一个整理。 关于Unity与iOS之间通信,参考【Unity3d】Unity与iOS之间通信 Unity(c#)调用Android (一)、编写Java代码 实际上,任何已经存在的Java代码…...
Allegro如何更改DRC尺寸大小操作指导
Allegro如何更改DRC尺寸大小操作指导 在做PCB设计的时候,DRC可以辅助设计,有的时候DRC的尺寸过大会影响视觉,Allegro支持将DRC的尺寸变小或者改大 如下图,DRC尺寸过大 如何改小,具体操作如下 点击Setup选择Design Parameters...

Mongodb WT_PANIC: WiredTiger library panic
文章目录故障现象排查过程1.查看Log2.同步恢复数据故障现象 周五突然收到Mongo实例莫名奇妙挂了告警,一般都是RS复制集架构模式(5节点),查看此实例角色为SECONDAR,挂了暂时不影响线上业务,但还是需要尽快修…...
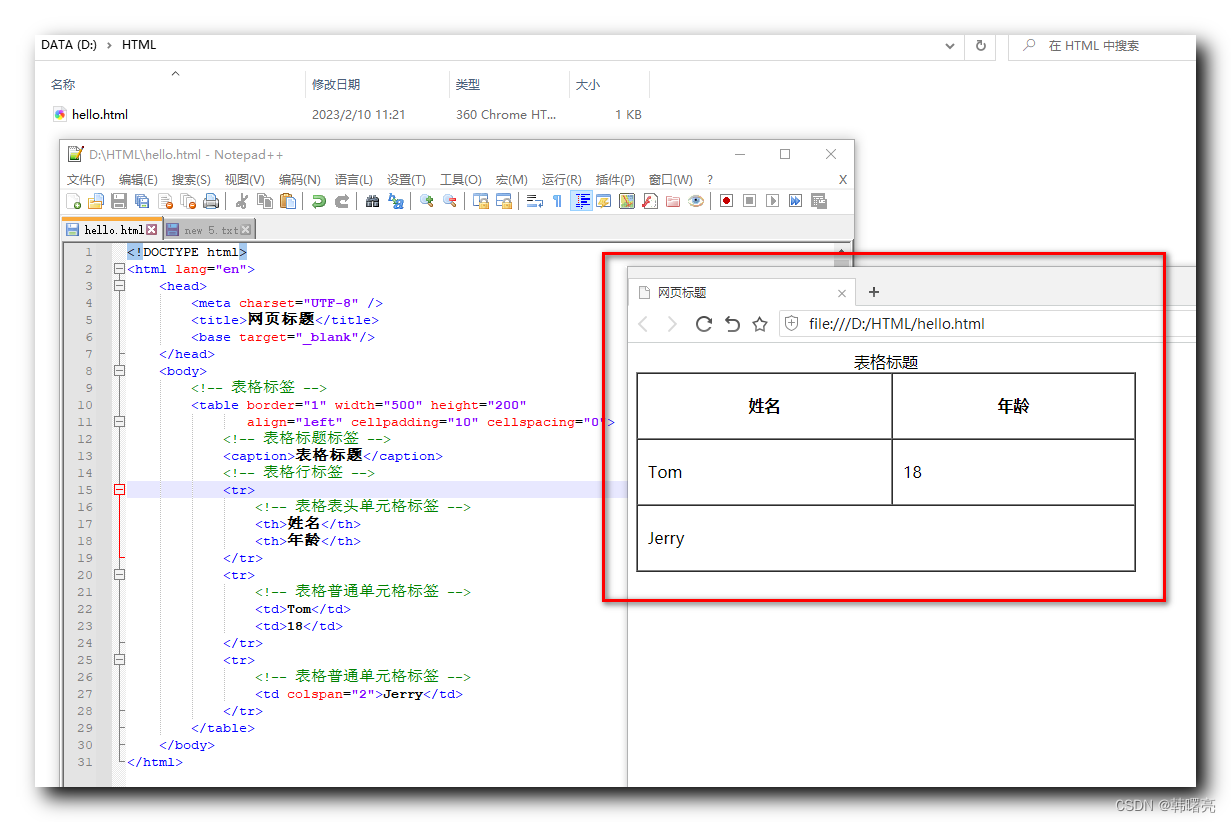
【HTML】HTML 表格总结 ★★★ ( 表格标签 | 行标签 | 单元格标签 | 表格标签属性 | 表头单元格标签 | 表格标题标签 | 合并单元格 )
文章目录一、表格标签组成 ( 表格标签 | 行标签 | 单元格标签 )二、table 表格属性 ( border 属性 | align 属性 | width 属性 | height 属性 )三、表头单元格标签四、表格标题标签五、合并单元格1、合并单元格方式2、合并单元格顺序3、合并单元格流程六、合并单元格示例1、原始…...

linux013之文件和目录的权限管理
用户、组、文件目录的关系: 简介:用户和组关联,组合文件目录关联,这样就实现了用户对文件的权限管理。首先来看一下,一个文件或目录的权限是怎么查看的,ls -l, 如下,这个信息怎么看呢…...
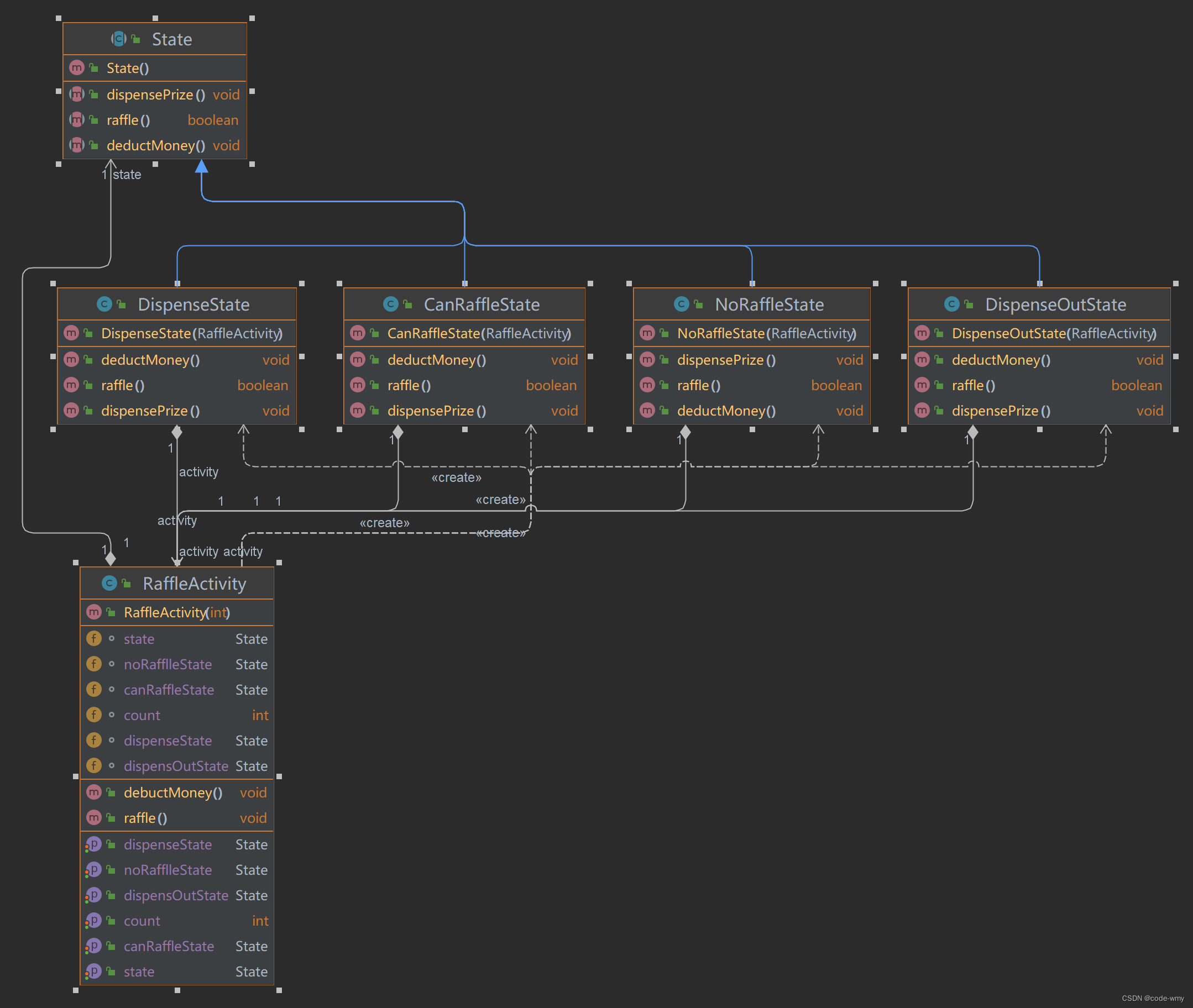
设计模式之状态模式
什么是状态模式 状态模式是指允许一个对象在其内部状态改变时改变他的行为,对象看起来似乎改变了整个类。 状态模式将一个对象在不同状态下的不同行为封装在一个个状态类中,通过设置不同的状态对象可以让环境对象拥有不同的行为,而状…...

XQuery 选择 和 过滤
XML实例文档 我们将在下面的例子中继续使用这个 "books.xml" 文档(和上面的章节所使用的 XML 文件相同)。 在您的浏览器中查看 "books.xml" 文件。 选择和过滤元素 正如在前面的章节所看到的,我们使用路径表达式或 FL…...

室友打了一把王者的时间,我理清楚了grep,find,管道|,xargs的区别与联系,用的时候不知道为什么要这样用
目录 问题引入 find和grep的基本区别 xargs命令 Linux命令的标准输入 vs 命令行参数 举例总结 问题引入 在自己做项目的过程中,想使用linux命令统计下一个目录下html文件的数量,在思考应该使用grep还是find去配合wc指令统计文件数量,后来…...
python 刷题时常见的函数
collections.OrderedDict 1. move_to_end() move_to_end() 函数可以将指定的键值对移动到最前面或者最后面,即最左边或最右边 。 2. popitem() popitem()可以完成元素的删除操作,有一个可选参数last(默认为True),…...

Python之列表推导式和列表排序
Python中的列表推导式,是小编比较喜欢的一种,他能大大减少你的代码量来得到你想要的结果,下面说说列表中常用的几种推导式 列表排序 Python开发中会经常用到排序操作,这里提供两种方式供大家参考,对象的sort()方法和…...

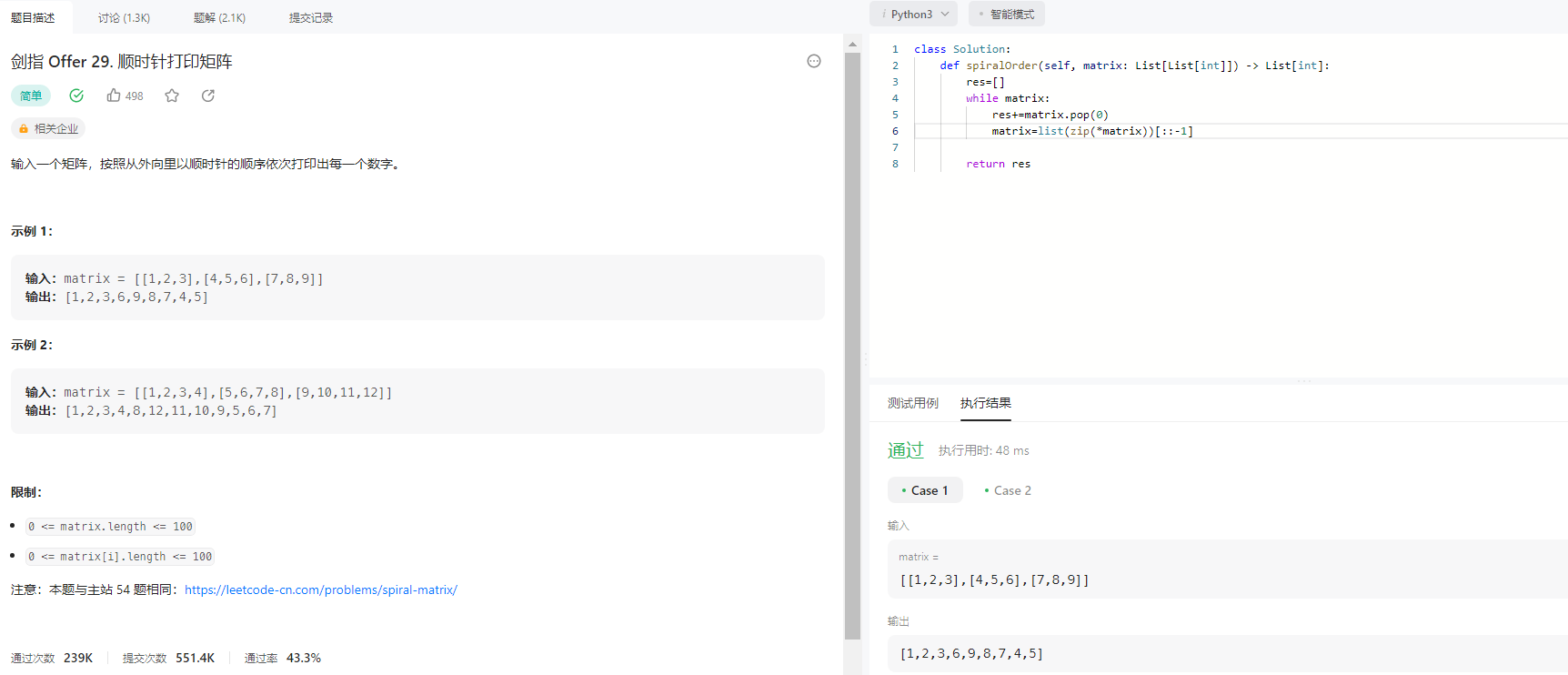
力扣(LeetCode)240. 搜索二维矩阵 II(C++)
题目描述 枚举 枚举整个矩阵,找到等于 target 的元素,则 return true ,否则 return false。 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n matrix.size(), m matrix[0]…...

golang defer
文章目录延迟函数的参数在defer语句出现时就已经确定下来了延迟函数没有入参时,延迟函数体内的变量会受到影响延迟函数 *可以* 修改主函数的 *具名* 返回值延迟函数 *无法* 修改主函数的 *匿名* 返回值defer会把声明的 延迟函数以及 函数的入参放到栈上,…...
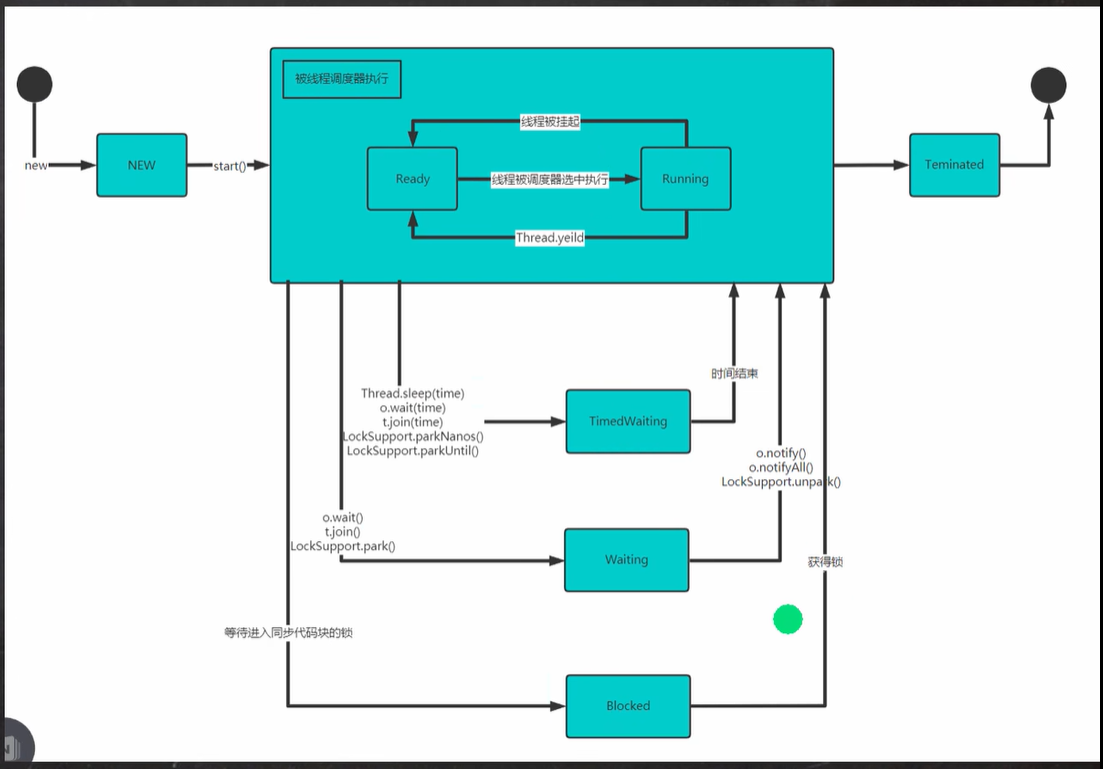
【Java】线程的死锁和释放锁
线程死锁是线程同步的时候可能出现的一种问题 文章目录1. 线程的死锁1.1 基本介绍1.2 应用案例2. 释放锁2.1 下面的操作会释放锁2.2 下面的操作不会释放锁1. 线程的死锁 1.1 基本介绍 多个线程都占用了对方的锁资源,但不肯相让,导致了死锁,…...
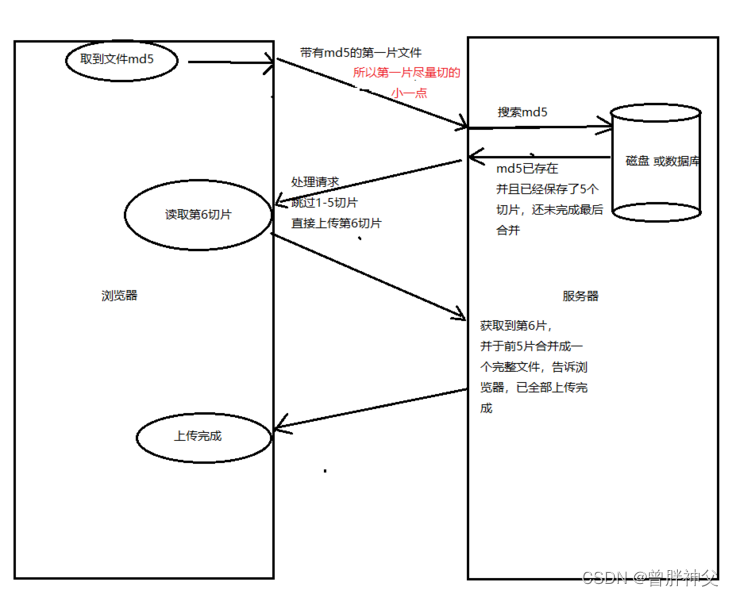
如何使用断点续传上传大文件
概念 大文件上传的需求介绍 不管怎样简单的需求,在量级达到一定层次时,都会变得异常复杂。 文件上传简单,文件变大就复杂 上传大文件时,以下几个变量会影响我们的用户体验 服务器处理数据的能力请求超时网络波动 上传时间会变长…...
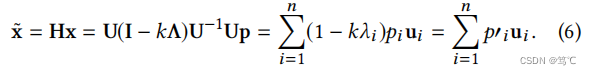
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波 文章目录【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波1. 前言2. 符号说明3. 三种滤波3.1 全通滤波3.2 低通滤波3.2.1 平滑信号分析3.2.2 广义拉普拉斯平滑滤波器3.3 高通滤波4. 总结1. 前言 GCN&…...

python操作mysql数据库详解
使用Python操作MySQL数据库 MySQL是一种关系型数据库管理系统,它可以用来存储和管理大量的数据。之前介绍了大部分主流数据库,今天将介绍如何使用Python来操作MySQL数据库。 安装MySQL 首先,我们需要安装MySQL服务器,可以从MyS…...
netty群聊系统
1设计思路:启动一个服务端,多个客户端第一个客户端启动时,会告诉服务器上线了第二个客户端启动时,告诉服务器上线,并且通知第一个启动的客户端第三个客户端启动时,告诉服务器上线,并且通知第一个…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
