【Python】缺失值处理和拉格朗日插值法(含源代码实现)
目录:缺失值处理和拉格朗日插值法
- 一、前言
- 二、理论知识
- 三、代码实现
一、前言
对于含有缺失值的数据集,如果通过删除小部分记录达到既定的目标,那么删除含有缺失值的记录的方法是最有效的。然而,这种方法也有很多问题,删除缺失值的同时也会损失一定的信息,对于那些数据集较小的来说这是影响很大的。
所以可以对这些缺失值进行填充。
最简单的处理原则:
- 缺失值少于20%
连续变量使用均值或者中位数填补;
分类变量不需要填补,单算一类即可,或者用众数填补。
- 缺失值在20%-80%
填补方法同上;
另外每个有缺失值的变量生成一个指示哑变量,参与后续的建模。
- 缺失值大于80%
每个有缺失值的变量生成一个指示哑变量,参与后续的建模,原始变量不使用。
也可以用最近邻插补法,可以在数据集中寻找与该样本除掉缺失属性最相近的样本,用相似的样本的属性值代替,求相似度可以采用聚类方法。
其次还有回归方法和插值法,回归方法及时建立回归模型,用已有的数据训练模型然后再预测。
插值法就有朗日插值法和牛顿插值法,这里就介绍一下拉格朗日插值法。
二、理论知识
下面是拉格朗日函数:
f(x)=∑i=1i=3yi∗∏i≠j1≤j≤3x−xjxi−xjf(x)=\sum_{i=1}^{i=3}y_i * \prod_{i\neq j}^{1\leq j \leq 3}\frac{x-x_j}{x_i-x_j} f(x)=i=1∑i=3yi∗i=j∏1≤j≤3xi−xjx−xj
如何得到这个函数的,分为下面几步:
三个点(x1,y1),(x2,y2),(x3,y3)(x_1,y_1),(x_2,y_2),(x_3,y_3)(x1,y1),(x2,y2),(x3,y3)可以确定一条二次多项式的函数。这需要把三个点带入多项式然后解出各个系数。
但是拉格朗日的这个解法就不一样了。
第一步构建了一个函数:
f1(x)=(x−x2)(x−x3)(x1−x2)(x1−x3)f_1(x)=\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)} f1(x)=(x1−x2)(x1−x3)(x−x2)(x−x3)
这个函数在x=x1x=x_1x=x1时,值为1;x=x2x=x_2x=x2时,值为0;x=x3x=x_3x=x3时,值为0。
同理分别构建:
f2(x)=(x−x1)(x−x3)(x2−x1)(x2−x3)f_2(x)=\frac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)} f2(x)=(x2−x1)(x2−x3)(x−x1)(x−x3)
这个函数在x=x2x=x_2x=x2时,值为1;x=x1x=x_1x=x1和x=x3x=x_3x=x3时,值为0。
f3(x)=(x−x1)(x−x2)(x3−x1)(x3−x2)f_3(x)=\frac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)} f3(x)=(x3−x1)(x3−x2)(x−x1)(x−x2)
这个函数在x=x3x=x_3x=x3时,值为1;在x=x1x=x_1x=x1和x=x2x=x_2x=x2时,值为0。
那么f(x)f(x)f(x)就可以写为:
f(x)=y1f1(x)+y2f2(x)+y3f3(x)f(x)=y_1f_1(x)+y_2f_2(x)+y_3f_3(x) f(x)=y1f1(x)+y2f2(x)+y3f3(x)
写为:
fi(x)=∏i≠j1≤j≤3(x−xj)(xi−xj)f_i(x)=\prod_{i\neq j}^{1\leq j \leq 3}\frac{(x-x_j)}{(x_i-x_j)} fi(x)=i=j∏1≤j≤3(xi−xj)(x−xj)
得到拉格朗日函数。
三、代码实现
from scipy.interpolate import lagrange
def lag_fill(df, i, k):r = 0 if (i - k) < 0 else (i - k)l = len(df.index) if (i + 1 + k) > len(df.index) else (i + 1 + k)y = df.loc[list(range(r, i)) + list(range(i + 1, l))]for j in y.index:if y.isnull().loc[j]:y.drop(index = j, inplace = True)x = y.indexlag = lagrange(x.values, y.values)return lag(i)
index = np.array(data['Age'][data['Age'].isnull()].index)
nums = []
for i in index:num = int(lag_fill(data['Age'], i, 5))nums.append(num)
df = data['Age'].copy()
index = np.array(df[df.isnull()].index) # 缺失值的索引
for i in range(len(index)):df.loc[index[i]] = nums[i]
df.isnull().sum()
结果为:
0
最后替换一下:
data['Age'] = df
data['Age'].isnull().sum()
相关文章:
)
【Python】缺失值处理和拉格朗日插值法(含源代码实现)
目录:缺失值处理和拉格朗日插值法一、前言二、理论知识三、代码实现一、前言 对于含有缺失值的数据集,如果通过删除小部分记录达到既定的目标,那么删除含有缺失值的记录的方法是最有效的。然而,这种方法也有很多问题,…...
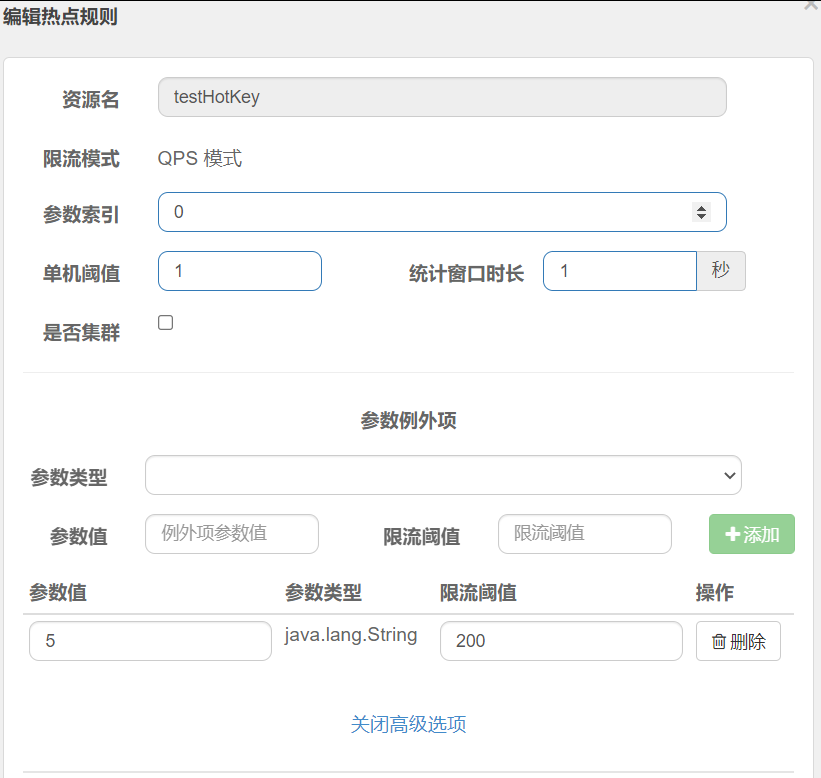
SpringCloudAlibaba-Sentinel
一、介绍官网:https://github.com/alibaba/Sentinel/下载jar包,启动,访问http://localhost:8080/创建module添加如下依赖<!--SpringCloud ailibaba sentinel --><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring…...

【程序化天空盒】过程记录02:云扰动 边缘光 消散效果
写在前面 写在前面唉,最近筋疲力竭,课题组的东西一堆没做,才刚刚开始带着思考准备练习作品,从去年5月份开始到现在真得学了快一年了,转行学其他的真的好累,,不过还是加油! 下面是做…...
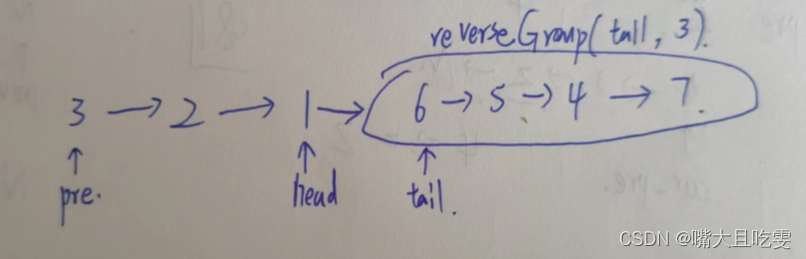
链表OJ(三) 反转链表合集
目录 反转链表 反转链表 II 链表中的节点每k个一组翻转 描述 给定一个单链表的头结点pHead(该头节点是有值的,比如在下图,它的val是1),长度为n,反转该链表后,返回新链表的表头。 数据范围: 0≤n≤10000≤…...
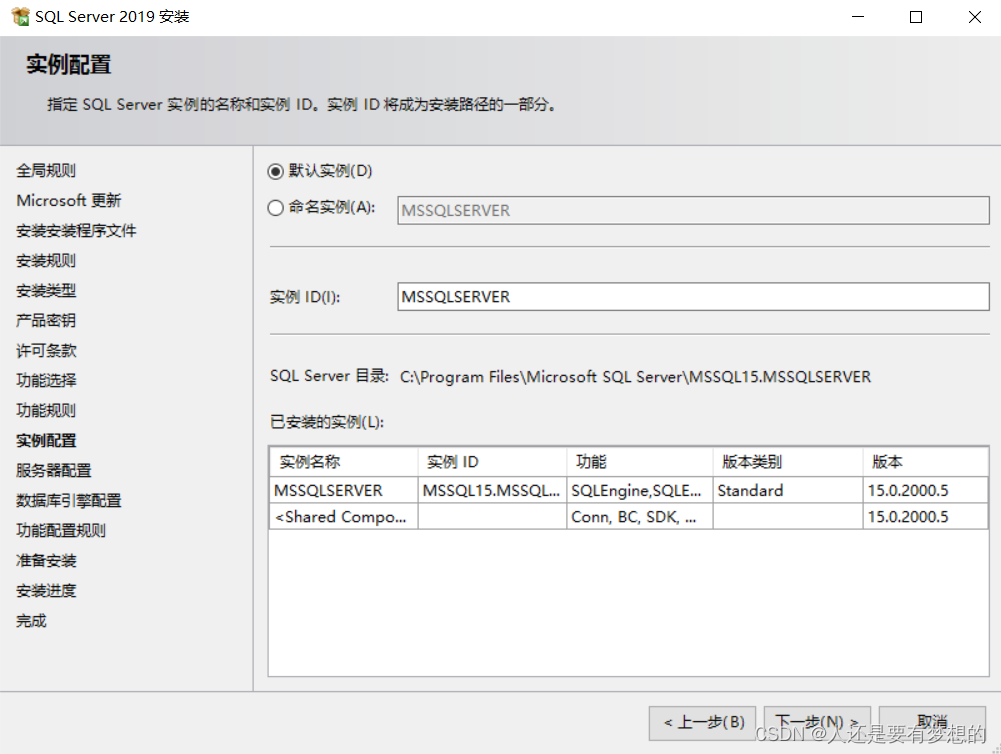
SQLSERVER2019安装步骤过程
第一步官网下载SQLSERVER软件包 目前官网只能下载最新版本2022版本。 通过迅雷下载网址 SQL Server 2019 Enterprise (x64) - DVD (Chinese-Simplified)企业版 ed2k://|file|cn_sql_server_2019_enterprise_x64_dvd_2bfe815a.iso|1632086016|58C258FF0F1D006DD3C1F5F17AF3E…...

Java模块化概述
3 模块化 3.1 模块化概述 Java语言随着这些年的发展已经成为了一]影响深远的编程语言,无数平台,系统都采用Java语言编写。但是,伴随着发展,Java也越来越庞大,逐渐发展成为-门“臃肿” 的语言。而且,无论是运行个大型的…...
)
Connext DDSPersistence Service持久性服务(2)
可选数据库组件及兼容性当Persistence Service配置为PERSISTENT模式时,您可以选择将主题数据存储在文件中还是存储在外部关系数据库中。 唯一支持的外部数据库是MySQL。 当PersistenceService在PERSISTENT模式下使用时,您可以将其配置为将DDS样本存储到关系数据库中,例如MyS…...

MongoDB
MongoDB 应用场景 在传统数据库(Mysql),在数据操作的 **High performance 对数据库高并发读写的需求、Hugu Storage 对海量数据的高效率存储和访问的需求、High Scalability && High Availability 对数据库高扩展和高可用性的需…...
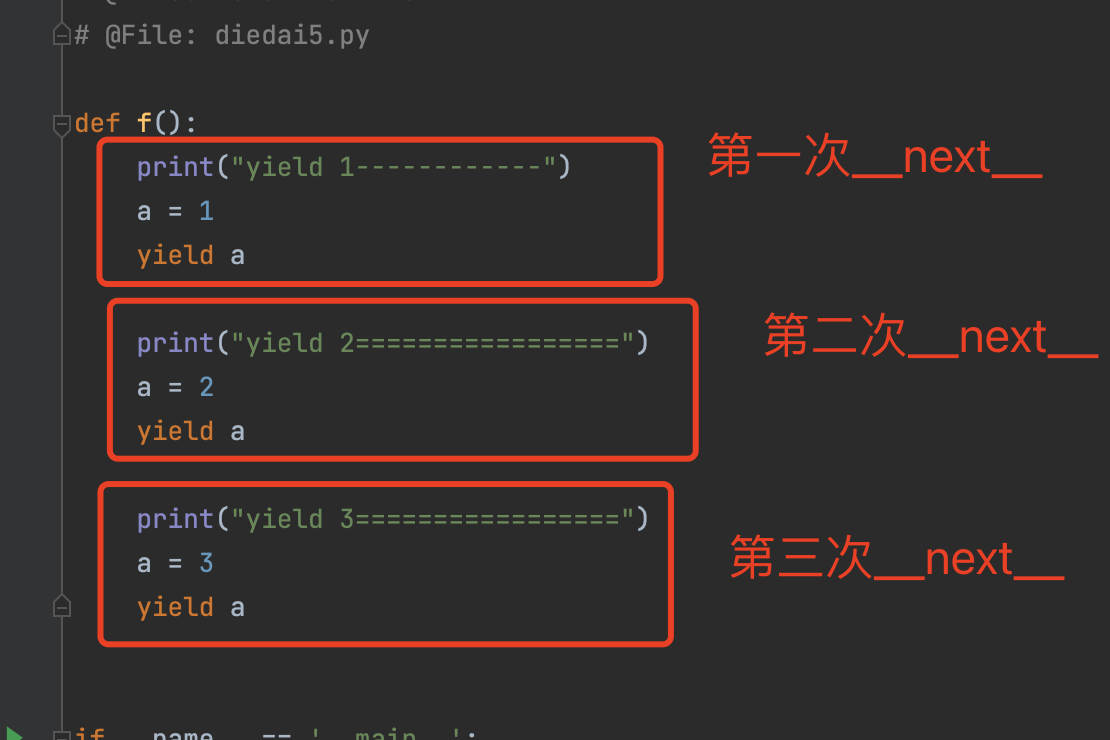
python 迭代器生成器
目录 一、可迭代对象 1.1 判断是否为可迭代对象 二、迭代器 2.1 判断对象是否是一个迭代器 2.2 手写一个迭代器 2.3 迭代器应用场景 三、生成器 3.1 生成器介绍 3.2 使用yield 关键字 生成器,来实现迭代器 3.3 生成器(yield关键字)…...

Iceberg基于Spark MergeInto语法实现数据的增量写入
SPARK SQL 基本语法 示例SQL如下 MERGE INTO target_table t USING source_table s ON s.id t.id //这里是JOIN的关联条件 WHEN MATCHED AND s.opType delete THEN DELETE // WHEN条件是对当前行进行打标的匹配条件 WHEN MATCHED AND s.opType update THEN…...
 对象)
JavaScript Array(数组) 对象
JavaScript 中的 Array(数组)对象是一种用来存储一系列值的容器,它可以包含任意类型的数据,包括数字、字符串、对象等等。通过使用数组对象,我们可以轻松地组织和处理数据,以及进行各种操作,比如…...

Debian如何更换apt源
中科大 deb https://mirrors.ustc.edu.cn/debian/ stretch main non-free contrib deb https://mirrors.ustc.edu.cn/debian/ stretch-updates main non-free contrib deb https://mirrors.ustc.edu.cn/debian/ stretch-backports main non-free contrib deb-src https://mirr…...

Connext DDSPersistence Service持久性服务
DDS持久性服务,它保存了DDS数据样本,以便即使发布应用程序已经终止,也可以稍后将其发送到加入系统的订阅应用程序。 简介Persistence Service是一个Connext DDS应用程序,它将DDS数据样本保存到临时或永久存储中,因此即使发布应用程序已经终止,也可以稍后将其交付给加入系…...
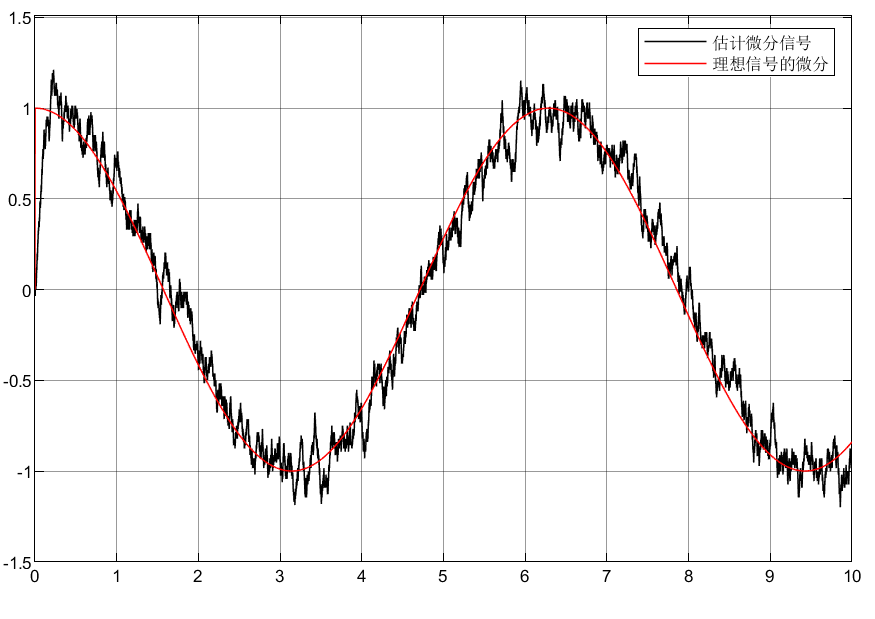
自抗扰控制ADRC之微分器TD
目录 前言 1 全程快速微分器 1.1仿真分析 1.2仿真模型 1.3仿真结果 1.4结论 2 Levant微分器 2.1仿真分析 2.2仿真模型 2.3仿真结果 3.总结 前言 工程上信号的微分是难以得到的,所以本文采用微分器实现带有噪声的信号及其微分信号提取,从而实现…...

链表学习之复制含随机指针的链表
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 复制含随机指针的链表 该链表节点的结构如下: class ListRandomNode { public:ListRandomNode() : val(0), next(nullptr), random(nullptr…...
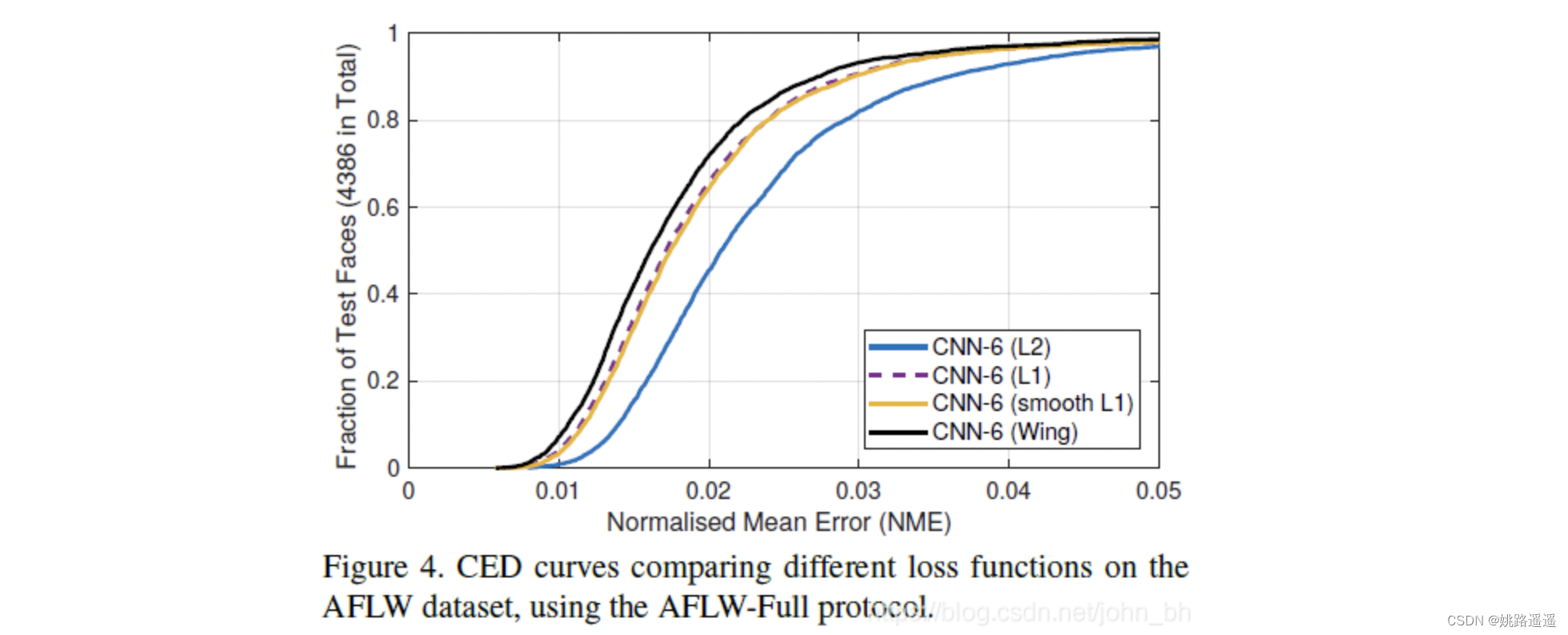
【人脸检测】Yolov5Face:优秀的one-stage人脸检测算法
论文题目:《YOLO5Face: Why Reinventing a Face Detector》 论文地址:https://arxiv.org/pdf/2105.12931.pdf 代码地址:https://github.com/deepcam-cn/yolov5-face 1.简介 近年来,CNN在人脸检测方面已经得到广泛的应用。但是许多…...
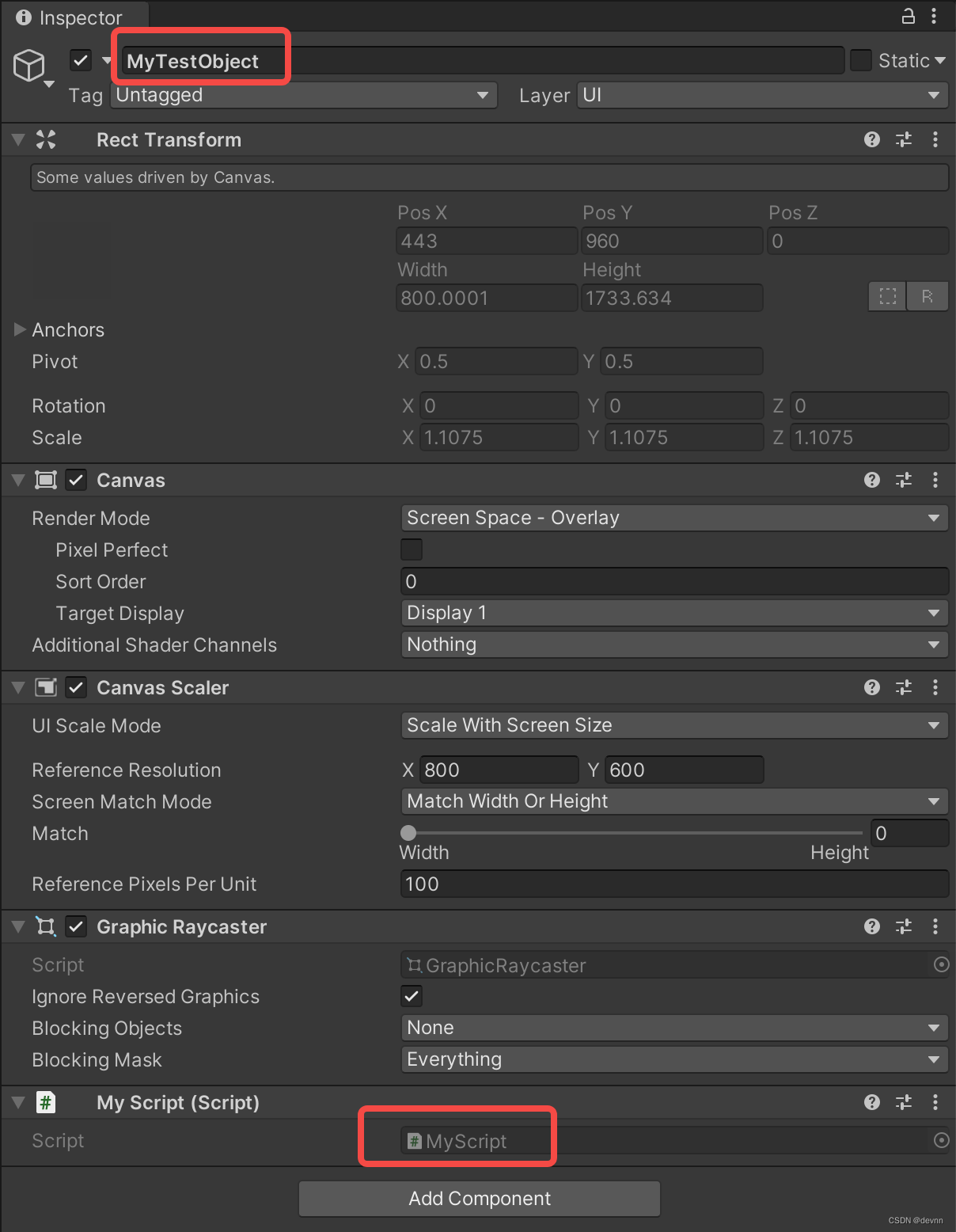
【Unity3d】Unity与Android之间通信
在unity开发或者sdk开发经常遇到unity与移动端原生层之间进行通信,这里把它们之间通信做一个整理。 关于Unity与iOS之间通信,参考【Unity3d】Unity与iOS之间通信 Unity(c#)调用Android (一)、编写Java代码 实际上,任何已经存在的Java代码…...
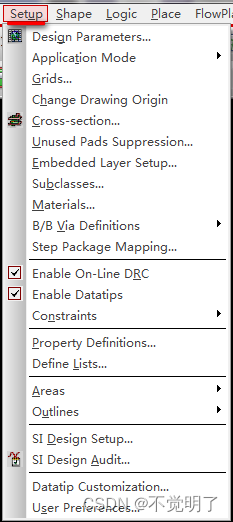
Allegro如何更改DRC尺寸大小操作指导
Allegro如何更改DRC尺寸大小操作指导 在做PCB设计的时候,DRC可以辅助设计,有的时候DRC的尺寸过大会影响视觉,Allegro支持将DRC的尺寸变小或者改大 如下图,DRC尺寸过大 如何改小,具体操作如下 点击Setup选择Design Parameters...

Mongodb WT_PANIC: WiredTiger library panic
文章目录故障现象排查过程1.查看Log2.同步恢复数据故障现象 周五突然收到Mongo实例莫名奇妙挂了告警,一般都是RS复制集架构模式(5节点),查看此实例角色为SECONDAR,挂了暂时不影响线上业务,但还是需要尽快修…...
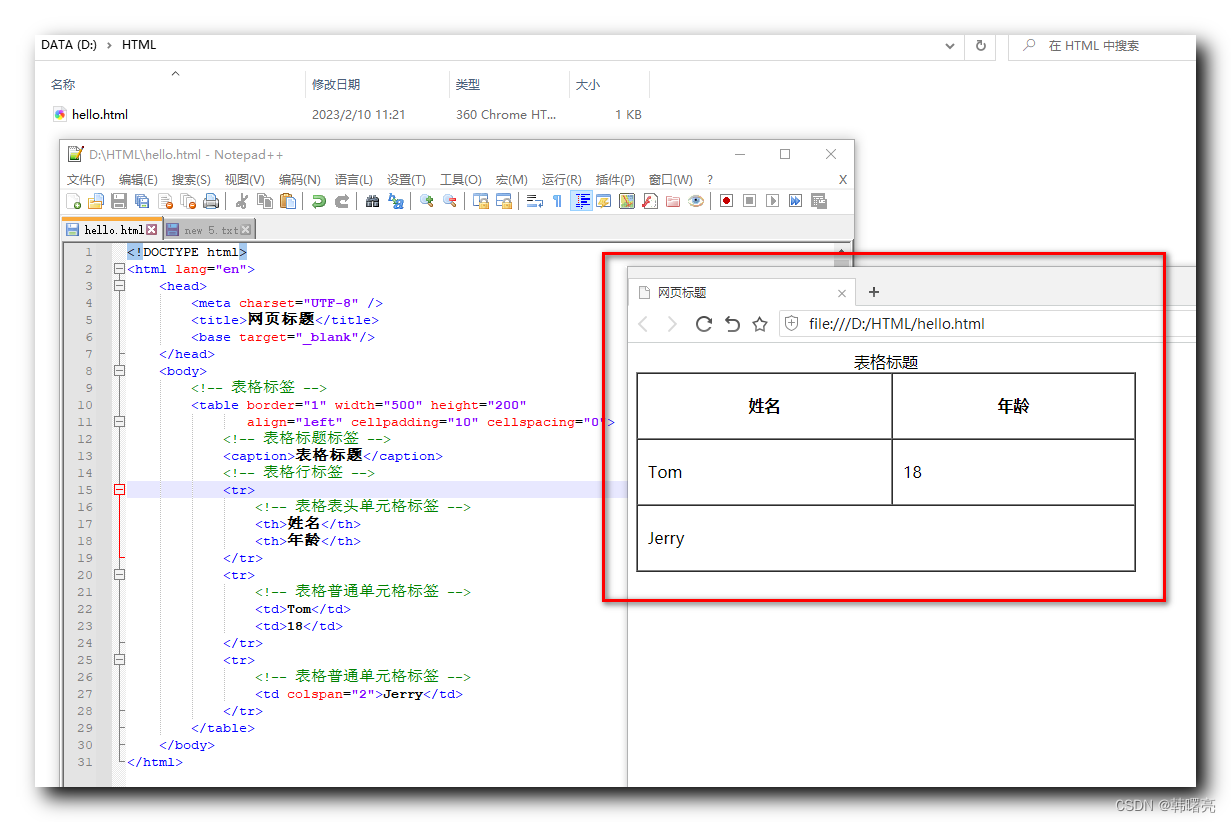
【HTML】HTML 表格总结 ★★★ ( 表格标签 | 行标签 | 单元格标签 | 表格标签属性 | 表头单元格标签 | 表格标题标签 | 合并单元格 )
文章目录一、表格标签组成 ( 表格标签 | 行标签 | 单元格标签 )二、table 表格属性 ( border 属性 | align 属性 | width 属性 | height 属性 )三、表头单元格标签四、表格标题标签五、合并单元格1、合并单元格方式2、合并单元格顺序3、合并单元格流程六、合并单元格示例1、原始…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

Qt Quick Controls模块功能及架构
Qt Quick Controls是Qt Quick的一个附加模块,提供了一套用于构建完整用户界面的UI控件。在Qt 6.0中,这个模块经历了重大重构和改进。 一、主要功能和特点 1. 架构重构 完全重写了底层架构,与Qt Quick更紧密集成 移除了对Qt Widgets的依赖&…...
