LeetCode 338. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
提示:
0 <= n <= 105
进阶:
很容易就能实现时间复杂度为 O(n log n) 的解决方案,你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗?
你能不使用任何内置函数解决此问题吗?(如,C++ 中的 __builtin_popcount )
解法一:动态规划,如3的比特位为1的位数等于将3右移一位(即1)的比特位为1的位数加上3&1:
class Solution {
public:vector<int> countBits(int n) {vector<int> ans(n + 1, 0);for (int i = 1; i <= n; ++i) {ans[i] = ans[i >> 1] + (i & 1);} return ans;}
};
此算法时间复杂度为O(n),空间复杂度为O(1)。
解法二:每个数字都计算一遍位数:
class Solution {
public:vector<int> countBits(int n) {vector<int> ans(n + 1, 0);for (int i = 1; i <= n; ++i) {int ibak = i;while (ibak) {ans[i] += ibak & 1;ibak >>= 1;}} return ans;}
};
此算法时间复杂度为O(nlgn),空间复杂度为O(1)。
解法三:使用库函数:
class Solution {
public:vector<int> countBits(int n) {vector<int> ans(n + 1, 0);for (int i = 1; i <= n; ++i) {ans[i] = __builtin_popcount(i);} return ans;}
};
此算法时间复杂度为O(nlgn),空间复杂度为O(1)。__builtin_popcount函数的时间复杂度为O(lgn)。
解法四:利用x&(x-1)的结果是x的最低的比特位从1变成0:
class Solution {
public:vector<int> countBits(int n) {vector<int> ans(n + 1, 0);for (int i = 1; i <= n; ++i) {int ibak = i;while (ibak) {ibak = ibak & (ibak - 1);ans[i] += 1;}} return ans;}
};
此算法时间复杂度为O(nlgn),空间复杂度为O(1)。
解法五:动态规划,最高位一定为1,x的比特位为1的计数等于去掉最高位后的数字的比特位为1的计数加上最高位的1:
class Solution {
public:vector<int> countBits(int n) {vector<int> ans(n + 1, 0);int highestBit = 0;for (int i = 1; i <= n; ++i) {// 当i是2的幂时,更新最高位if ((i & (i - 1)) == 0) {highestBit = i;}ans[i] = ans[i - highestBit] + 1;} return ans;}
};
此算法时间复杂度为O(n),空间复杂度为O(1)。
解法六:动态规划,x的比特位为1的计数等于把x的最低位的1改为0后的数的比特位为1的计数加上最低位的1:
class Solution {
public:vector<int> countBits(int n) {vector<int> ans(n + 1, 0);for (int i = 1; i <= n; ++i) {ans[i] = ans[i & (i - 1)] + 1;} return ans;}
};
此算法时间复杂度为O(n),空间复杂度为O(1)。
相关文章:

LeetCode 338. 比特位计数
给你一个整数 n ,对于 0 < i < n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n 1 的数组 ans 作为答案。 示例 1: 输入:n 2 输出:[0,1,1] 解释: 0 --> 0 1 --> …...
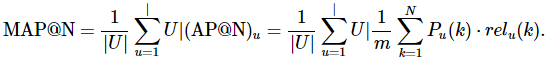
排序评估指标——NDCG和MAP
在搜索和推荐任务中,系统常返回一个item列表。如何衡量这个返回的列表是否优秀呢? 例如,当我们检索【推荐排序】,网页返回了与推荐排序相关的链接列表。列表可能会是[A,B,C,G,D,E,F],也可能是[C,F,A,E,D],现在问题来了…...

[Android Studio] Android Studio Virtual Device(AVD)虚拟机的功能试用
🟧🟨🟩🟦🟪 Android Debug🟧🟨🟩🟦🟪 Topic 发布安卓学习过程中遇到问题解决过程,希望我的解决方案可以对小伙伴们有帮助。 🚀write…...
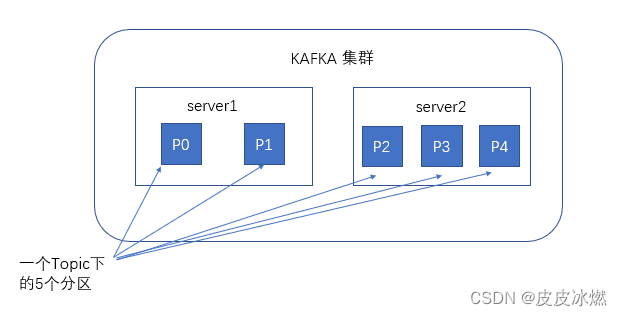
kafka-3-kafka应用的核心要点和内外网访问
kafka实战教程(python操作kafka),kafka配置文件详解 Kafka内外网访问的设置 1 kafka简介 根据官网的介绍,ApacheKafka是一个分布式流媒体平台,它主要有3种功能: (1)发布和订阅消息流,这个功能类似于消息队列&#x…...
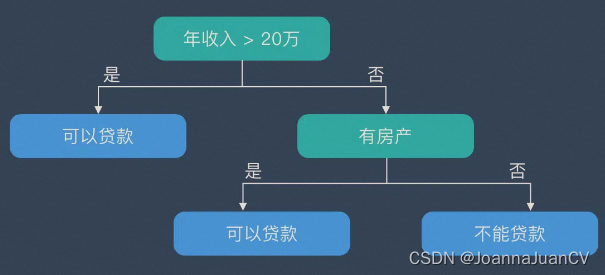
VS2017+OpenCV4.5.5 决策树-评估是否发放贷款
决策树是一种非参数的监督学习方法,主要用于分类和回归。 决策树结构 决策树在逻辑上以树的形式存在,包含根节点、内部结点和叶节点。 根节点:包含数据集中的所有数据的集合内部节点:每个内部节点为一个判断条件,并且…...

Prometheus 记录规则和警报规则
前提环境: Docker环境 涉及参考文档: Prometheus 录制规则Prometheus 警报规则 语法检查规则 promtool check rules /path/to/example.rules.yml一:录制规则语法 groups 语法: groups:[ - <rule_group> ]rule_group…...

(API)接口测试的关键技术
接口测试也就是API测试,从名字上可以知道是面向接口的测试活动。所以在讲API测试之前,我们应该说清楚接口是什么,那么接口就是有特定输入和特定输出的一套逻辑处理单元,而对于接口调用方来说,不用知道自身的内部实现逻…...

快速排序算法原理 Quicksort —— 图解(精讲) JAVA
快速排序是 Java 中 sort 函数主要的排序方法,所以今天要对快速排序法这种重要算法的详细原理进行分析。 思路:首先快速排序之所以高效一部分原因是利用了离散数学中的传递性。 例如 1 < 2 且 2 < 3 所以可以推出 1 < 3。在快速排序的过程中巧…...

linux环境搭建私有gitlab仓库
搭建之前,需要安装相应的依赖包,并且要启动sshd服务(1).安装policycoreutils-python openssh-server openssh-clients [rootVM-0-2-centos ~]# sudo yum install -y curl policycoreutils-python openssh-server openssh-clients [rootVM-0-2-centos ~]…...

SpringSecurity授权
文章目录工具类使用自定义失败处理代码配置跨域其他权限授权hasAnyAuthority自定义权限校验方法基于配置的权限控制工具类 import javax.servlet.http.HttpServletResponse; import java.io.IOException;public class WebUtils {/*** 将字符串渲染到客户端** param response 渲…...

学习 Python 之 Pygame 开发坦克大战(一)
学习 Python 之 Pygame 开发坦克大战(一)Pygame什么是Pygame?初识pygame1. 使用pygame创建窗口2. 设置窗口背景颜色3. 获取窗口中的事件4. 在窗口中展示图片(1). pygame中的直角坐标系(2). 展示图片(3). 给部分区域设置颜色5. 在窗口中显示文字6. 播放音…...

2.5|iot冯|方元-嵌入式linux系统开发入门|2.13+2.18
一、 Linux 指令操作题(共5题(共 20 分,每小题 4分)与系统工作、系统状态、工作目录、文件、目录、打包压缩与搜索等主题相关。1.文件1.1文件属性1.2文件类型属性字段的第1个字符表示文件类型,后9个字符中,…...
)
一起Talk Android吧(第四百九十六回:自定义View实例二:环形进度条)
文章目录 知识回顾实现思路实现方法示例代码各位看官们大家好,上一回中咱们说的例子是"如何使用Java版MQTT客户端",这一回中咱们说的例子是"自定义View实例二:环形进度条"。闲话休提,言归正转,让我们一起Talk Android吧! 知识回顾 看官们,我们又回…...

上传图片尺寸校验
使用方法 ● Image ● URL ● onload代码: async validImageSize(file, imgWidth, imgHeight) {const img new Image()img.src URL.createObjectURL(file)const { w, h } await new Promise((resolve, reject) > {img.onload () > {const { width: w, he…...
)
【Python】缺失值处理和拉格朗日插值法(含源代码实现)
目录:缺失值处理和拉格朗日插值法一、前言二、理论知识三、代码实现一、前言 对于含有缺失值的数据集,如果通过删除小部分记录达到既定的目标,那么删除含有缺失值的记录的方法是最有效的。然而,这种方法也有很多问题,…...
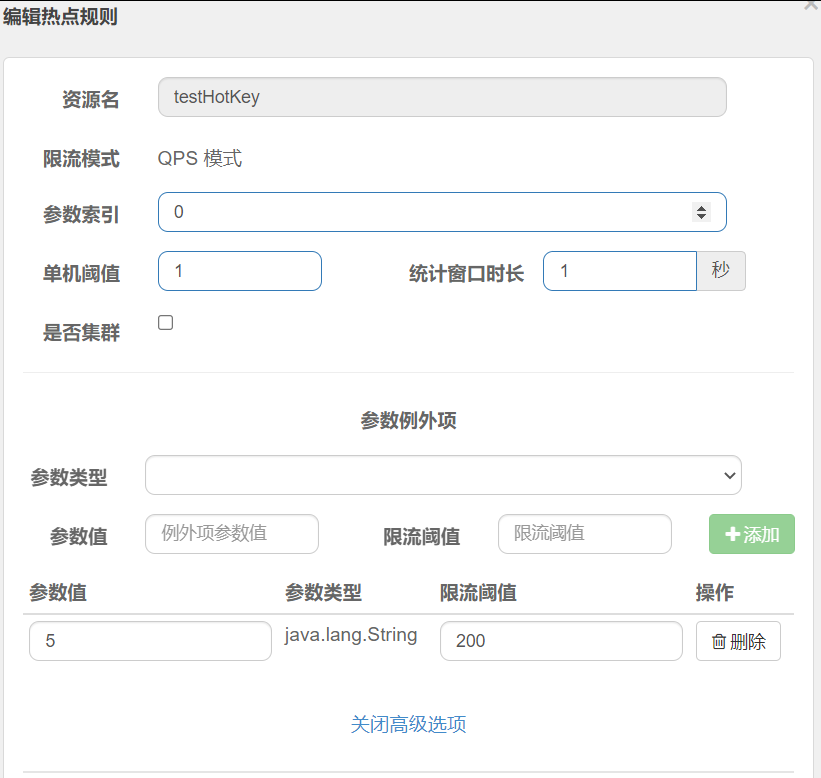
SpringCloudAlibaba-Sentinel
一、介绍官网:https://github.com/alibaba/Sentinel/下载jar包,启动,访问http://localhost:8080/创建module添加如下依赖<!--SpringCloud ailibaba sentinel --><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring…...

【程序化天空盒】过程记录02:云扰动 边缘光 消散效果
写在前面 写在前面唉,最近筋疲力竭,课题组的东西一堆没做,才刚刚开始带着思考准备练习作品,从去年5月份开始到现在真得学了快一年了,转行学其他的真的好累,,不过还是加油! 下面是做…...
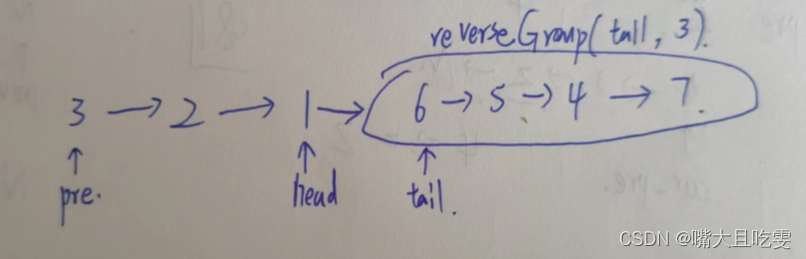
链表OJ(三) 反转链表合集
目录 反转链表 反转链表 II 链表中的节点每k个一组翻转 描述 给定一个单链表的头结点pHead(该头节点是有值的,比如在下图,它的val是1),长度为n,反转该链表后,返回新链表的表头。 数据范围: 0≤n≤10000≤…...
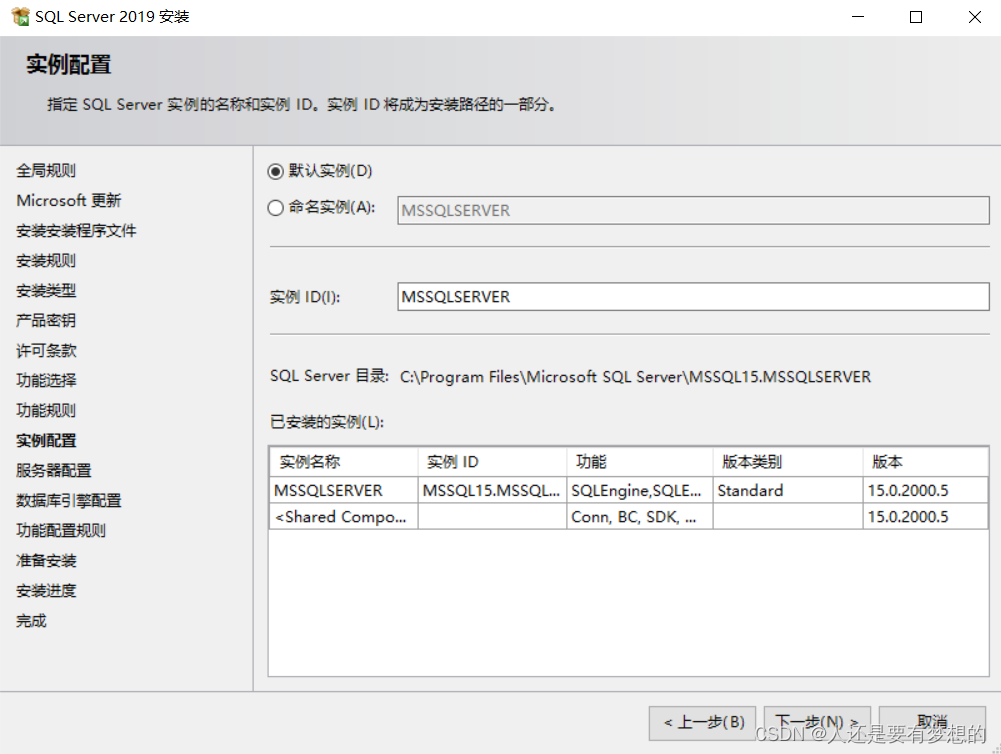
SQLSERVER2019安装步骤过程
第一步官网下载SQLSERVER软件包 目前官网只能下载最新版本2022版本。 通过迅雷下载网址 SQL Server 2019 Enterprise (x64) - DVD (Chinese-Simplified)企业版 ed2k://|file|cn_sql_server_2019_enterprise_x64_dvd_2bfe815a.iso|1632086016|58C258FF0F1D006DD3C1F5F17AF3E…...

Java模块化概述
3 模块化 3.1 模块化概述 Java语言随着这些年的发展已经成为了一]影响深远的编程语言,无数平台,系统都采用Java语言编写。但是,伴随着发展,Java也越来越庞大,逐渐发展成为-门“臃肿” 的语言。而且,无论是运行个大型的…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
