二维数组中的查找(两种解法,各有千秋)
凡事都有可能,永远别说永远。——《放牛班的春天》
今天一题为再一个行列都有序的二维数组中寻找一个目标值,我们第一时间想到的可能是很暴力的解法,例如从头到尾进行遍历,这样能做出来,但是借用武忠祥老师的一句话:这样做你就慢了,没效率。
本文章会从复杂度的角度来分析一个算法,循序渐进的提升这个算法的优秀程度。最终优化为最优算法。
一.题目及示例
在一个二维数组array中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7,返回 true。
给定 target = 3,返回 false。下面给出示例:

解法一(暴力解法):
拿到这道题目,第一种方法不难想到,就是对整个数组进行遍历,每一个元素都扫一遍。这种解法比较暴躁,很暴力,给它一个外号,叫"暴力解法"。
具体代码实现如下:
bool Find(int target, vector<vector<int> > array) {// 利用C++的auto进行遍历for(auto x:array) {for(auto y:x){// 如果存在,直接返回trueif(y==target){return true;}}}return false;ps:这里的for循环不是普通的for循环,这是C++新定义的for循环,具体使用可以去看我下一篇博客。
我把他称之为升级版for循环。
复杂度分析:
需要对二维数组的每个元素进行遍历,时间复杂度为O(n^2)
存储一个二维数组,空间复杂度为O(1)
解法二(双指针法)
由于矩阵行列都是严格递增的,此矩阵为杨氏矩阵,故也称杨氏矩阵法。
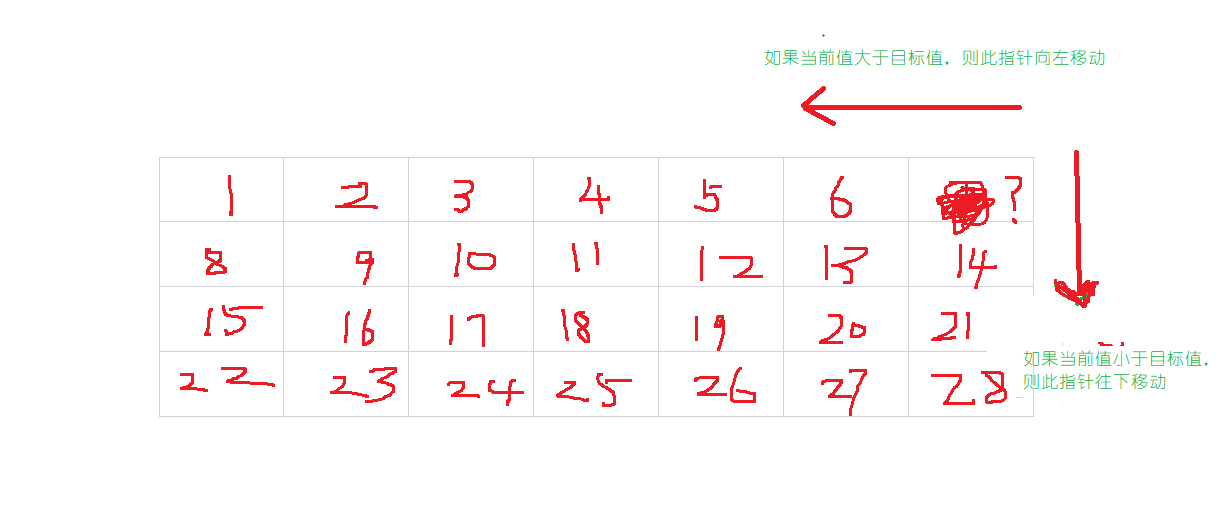
如果这个是一个没有任何规律的数组,那么可能就只有那种写法了,但是这个题目(红字)告诉我们这个数字从上到下,从左到右都是递增的,所以我们可以从这个方向入手。我们发现,我们找一个数,最快的办法无非就是利用二分进行查找,但是我们发现这个题目是一个二维单调的。所以我们要想办法找到一个方法可以在我们判断到数字小了或者大了的时候可以进行一个范围的缩小。这样的话,我们就可以定义两个指针,放到右上角或者左下角。这里我放到右上角进行讨论。
初始的时候,我们的两个x和y的指针放到了右上角。这样的话我们可以与目标数进行比较,如果发现这个数比目标数小了,我们就把y指针往下进行移动,y指针自增。如果发现这个数比目标数大了,我们就可以往左边方向进行移动,x指针自减。
具体代码实现如下:
(右上角代码)
bool Find(int target, vector<vector<int> > array) {int len1=array.size(); // 计算行数int len2=array[0].size(); //计算列数int posx=0,posy=len2-1; //定义两个指针,分别指向x和y的坐标while(posx<len1&&posy>=0){// 当前的数字比目标数字大,x指针左移if(array[posx][posy]>target){posy--;// 当前的数字比目标数字小,y指针往下移动}else if(array[posx][posy]<target){posx++;}else{return true;}}return false;}(左下角代码)
bool Find(int target, vector<vector<int> > array) {int len1=array.size(); // 行数int len2=array[0].size(); //列数int posx=len1-1,posy=0; // 定义两个指针,分别表示x和y的指针while(posx>=0&&posy<len2){// 当前的数字比目标数字大,x指针往上移动if(array[posx][posy]>target){posx--;// 当前的数字比目标数字小,y指针往右方向移动}else if(array[posx][posy]<target){posy++;}else{return true;}}return false;}复杂度分析:
由于x和y分别只能往一个方向进行移动。
右上角版,最有最多只会遍历一行和一列的长度,时间复杂度为O(n+m)
二维数组存储所有的元素,空间的复杂度为O(1)
我们做个总结,相对于第一题,第二题的时间复杂度从n^2到m+n得到提升,提升的原因就是很好的利用升序这个特点来优化。
相关文章:

二维数组中的查找(两种解法,各有千秋)
凡事都有可能,永远别说永远。——《放牛班的春天》今天一题为再一个行列都有序的二维数组中寻找一个目标值,我们第一时间想到的可能是很暴力的解法,例如从头到尾进行遍历,这样能做出来,但是借用武忠祥老师的一句话&…...
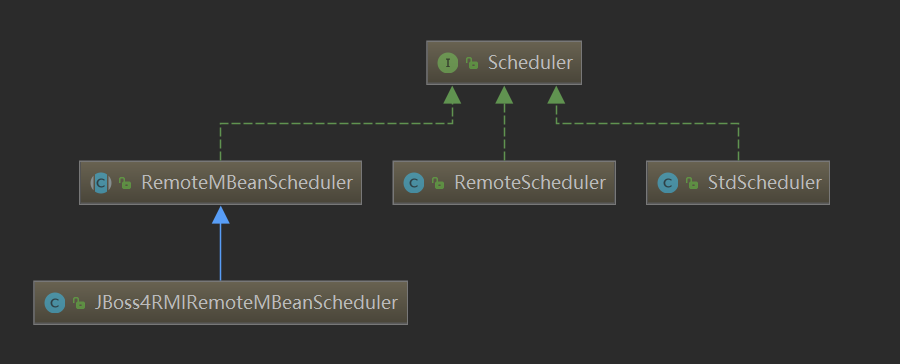
quartz使用及原理解析
quartz简介 Quartz是OpenSymphony开源组织在Job scheduling领域又一个开源项目,完全由Java开发,可以用来执行定时任务,类似于java.util.Timer。但是相较于Timer, Quartz增加了很多功能: 持久性作业 - 就是保持调度…...

Datawhale组队学习:大数据 D2——分布式文件系统(HDFS)
妙趣横生大数据 Day2三、Hadoop 分布式文件系统(HDFS)1. 分布式文件系统2. HDFS 简介3. HDFS 体系结构4. HDFS存储原理数据冗余存储数据存储策略数据错误与恢复5. HDFS数据读写过程读写过程HDFS故障类型和其检测方法HDFS编程实验1. 本地和集群文件间操作2. 基本文件操作3. Hado…...
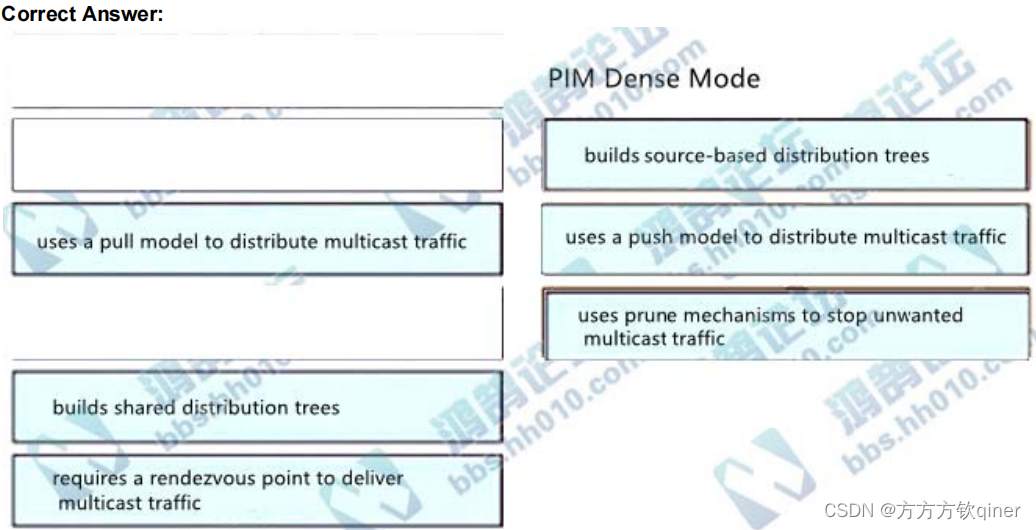
CCIE重认证-300-401-拖图题全
拖图 拖图题 编程 snippet;192.168.5.0,mask 255.255.255.0;number是192.168.5.0;mask是255.255.255.0 snippets;edit-config对config,loopback对name 100,address对primary,mask…...

如何动态的创建类?type的其他用法?什么是元类,如何自定义元类?
1、python中一切都是对象,类也不例外,type是object的子类,是创建类的类。 如何动态的创建一个类? 用脚丫子创建 用脑子创建 不会 不知道什么事动态类 大家可能会有一堆的疑惑,是的我也是有很多疑惑那让我们一起来探个…...

XCP实战系列介绍15-XCP故障排查指导
本文框架 1.概述2. 通过调试器排查2.1 打开Det功能2.2 如何确定Det ErrorCode3. 通过XCP应答报文排查3.1 FE报文组成及故障码对应关系3.2 举个例子1.概述 前面几篇文章我们介绍了基于Davinci开发工具的XCP配置指导,配好了,代码也生成了,但是程序一定能正常跑起来吗?就算软…...

吉林大学软件需求分析与规范(Software Requirements Analysis Specification)
chapter0课程简介:◼ 软件工程专业核心课程之一◼ 软件工程课程体系最前端课程◼ 主要内容:需求的基本概念,需求的分类,需求工程的基本过程,需求获取的方法、步骤、技巧,需求分析和建模技术,需求…...
PyTorch - Conv2d 和 MaxPool2d
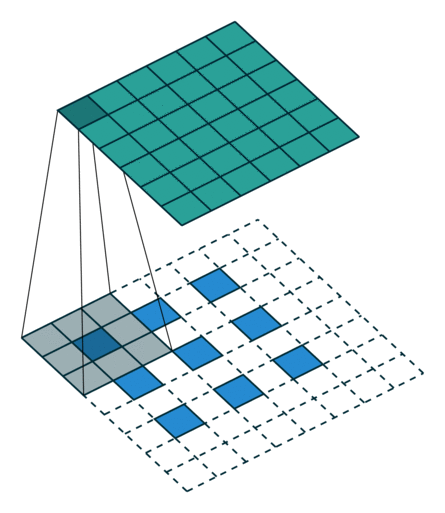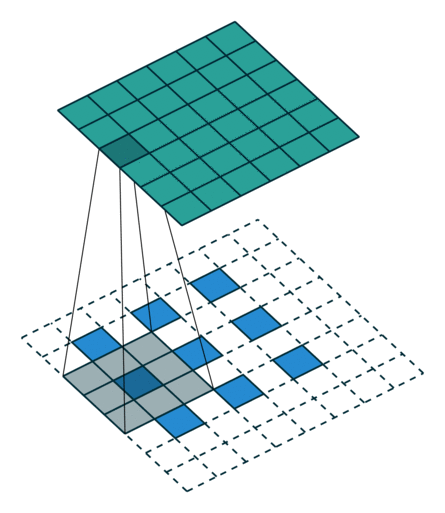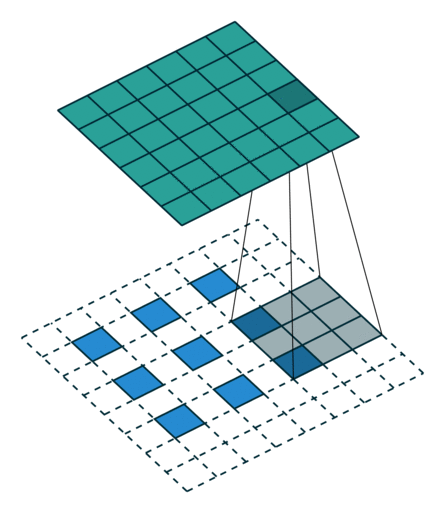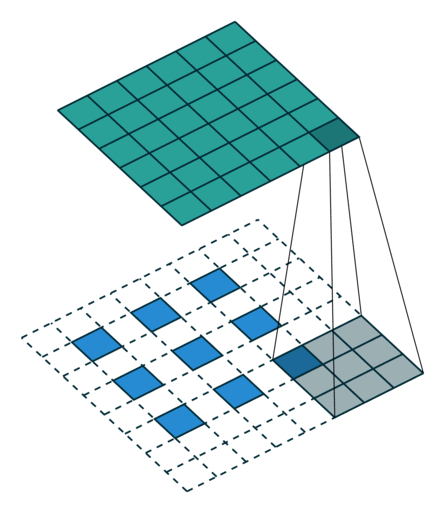
文章目录Conv2d计算Conv2d 函数解析代码示例MaxPool2d计算函数说明卷积过程动画Transposed convolution animationsTransposed convolution animations参考视频:土堆说 卷积计算 https://www.bilibili.com/video/BV1hE411t7RN 关于 torch.nn 和 torch.nn.function t…...
)
leetcode Day2(昨天实习有点bug,心态要崩了)
int carry 0;for(int i a.size() - 1, j b.size() - 1; i > 0 || j > 0 || carry; --i, --j) {int x i < 0 ? 0 : a[i] - 0;int y j < 0 ? 0 : b[j] - 0;int sum (x y carry) % 2;carry (x y carry) / 2;str.insert(0, 1, sum 0);}return str;加一&a…...

另一种思考:为什么不选JPA、MyBatis,而选择JDBCTemplate
以下内容转载自:https://segmentfault.com/a/1190000018472572 作者:scherman 因为项目需要选择数据持久化框架,看了一下主要几个流行的和不流行的框架,对于复杂业务系统,最终的结论是,JOOQ是总体上最好的…...

LeetCode 338. 比特位计数
给你一个整数 n ,对于 0 < i < n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n 1 的数组 ans 作为答案。 示例 1: 输入:n 2 输出:[0,1,1] 解释: 0 --> 0 1 --> …...
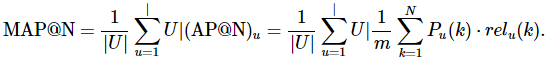
排序评估指标——NDCG和MAP
在搜索和推荐任务中,系统常返回一个item列表。如何衡量这个返回的列表是否优秀呢? 例如,当我们检索【推荐排序】,网页返回了与推荐排序相关的链接列表。列表可能会是[A,B,C,G,D,E,F],也可能是[C,F,A,E,D],现在问题来了…...

[Android Studio] Android Studio Virtual Device(AVD)虚拟机的功能试用
🟧🟨🟩🟦🟪 Android Debug🟧🟨🟩🟦🟪 Topic 发布安卓学习过程中遇到问题解决过程,希望我的解决方案可以对小伙伴们有帮助。 🚀write…...
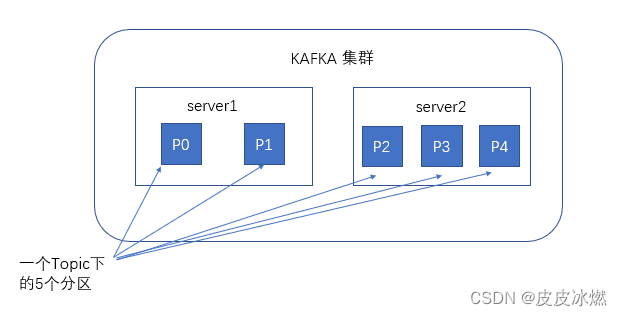
kafka-3-kafka应用的核心要点和内外网访问
kafka实战教程(python操作kafka),kafka配置文件详解 Kafka内外网访问的设置 1 kafka简介 根据官网的介绍,ApacheKafka是一个分布式流媒体平台,它主要有3种功能: (1)发布和订阅消息流,这个功能类似于消息队列&#x…...
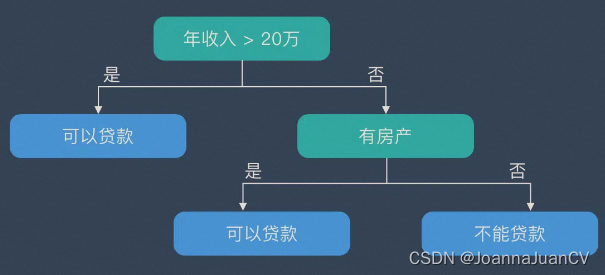
VS2017+OpenCV4.5.5 决策树-评估是否发放贷款
决策树是一种非参数的监督学习方法,主要用于分类和回归。 决策树结构 决策树在逻辑上以树的形式存在,包含根节点、内部结点和叶节点。 根节点:包含数据集中的所有数据的集合内部节点:每个内部节点为一个判断条件,并且…...

Prometheus 记录规则和警报规则
前提环境: Docker环境 涉及参考文档: Prometheus 录制规则Prometheus 警报规则 语法检查规则 promtool check rules /path/to/example.rules.yml一:录制规则语法 groups 语法: groups:[ - <rule_group> ]rule_group…...

(API)接口测试的关键技术
接口测试也就是API测试,从名字上可以知道是面向接口的测试活动。所以在讲API测试之前,我们应该说清楚接口是什么,那么接口就是有特定输入和特定输出的一套逻辑处理单元,而对于接口调用方来说,不用知道自身的内部实现逻…...

快速排序算法原理 Quicksort —— 图解(精讲) JAVA
快速排序是 Java 中 sort 函数主要的排序方法,所以今天要对快速排序法这种重要算法的详细原理进行分析。 思路:首先快速排序之所以高效一部分原因是利用了离散数学中的传递性。 例如 1 < 2 且 2 < 3 所以可以推出 1 < 3。在快速排序的过程中巧…...

linux环境搭建私有gitlab仓库
搭建之前,需要安装相应的依赖包,并且要启动sshd服务(1).安装policycoreutils-python openssh-server openssh-clients [rootVM-0-2-centos ~]# sudo yum install -y curl policycoreutils-python openssh-server openssh-clients [rootVM-0-2-centos ~]…...

SpringSecurity授权
文章目录工具类使用自定义失败处理代码配置跨域其他权限授权hasAnyAuthority自定义权限校验方法基于配置的权限控制工具类 import javax.servlet.http.HttpServletResponse; import java.io.IOException;public class WebUtils {/*** 将字符串渲染到客户端** param response 渲…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
