二叉树(一)
二叉树(一)
- 1.树的概念
- 2.树的相关概念
- 3.树的表示
- 4.树在实际中的运用
- 5.二叉树概念及结构
- 6.特殊的二叉树
- 7.二叉树的性质
🌟🌟hello,各位读者大大们你们好呀🌟🌟
🚀🚀系列专栏:【数据结构的学习】
📝📝本篇内容:树的概念;树的相关概念;树的表示;树在实际中的运用;二叉树概念及结构;特殊二叉树;二叉树的性质
⬆⬆⬆⬆上一篇:Linux进程概念(二)
💖💖作者简介:轩情吖,请多多指教(> •̀֊•́ ) ̖́-
1.树的概念
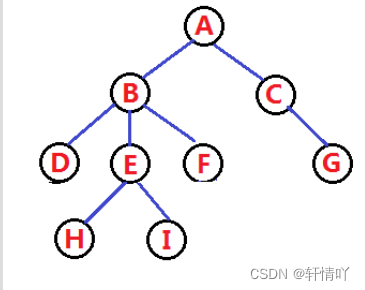
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成的一个有层次关系的集合
有一个特殊的结点,称为根结点,根结点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合,其中每一个集合又是一棵结构与树类似的子树。每棵子树的根节点有且只有一个前驱,可以有0个或者多个后继
任何一棵树,分解为根和N棵子树(N>=0)
因此树是递归定义的
注意:
①树形结构中,子树之间不能有交集,否则就不是树形结构
②子树是不相交的
③除了根结点外,每个结点有且只有一个父节点
④一棵N个结点的树有N-1条边
2.树的相关概念

结点的度:一个结点含有的子树个数称为该结点的度;如上图:A的为6
叶节点或终端结点:度为0的结点称为叶结点;如上图:B、C、H、I等结点为叶结点
非终端结点或分支结点:度不为0的结点;如上图:D、E、F、G等结点分支结点
双亲结点或父结点:若一个结点含有子节点,则这个结点称为其子结点的父结点;如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根节点称为该结点的子结点;如上图:B是A的子结点
兄弟结点:具有相同父结点的结点互称为兄弟结点;如上图:B、C是兄弟结点
树的度:一棵树中,最大的结点的度称为树的度;如上图:树的度为6
结点的层次:从根开始定义起,根为第一层,根的子结点为第二层,以此类推
树的高度或深度:树中结点的最大层次;如上图:树的高度为4
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、L互为堂兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由(m>0)棵互不相交的树的集合称为森林
3.树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};

4.树在实际中的运用
Linux树状目录结构

我们的windows的文件系统是树林,它分为好几棵树,对应C盘D盘等
5.二叉树概念及结构
一棵二叉树是结点的一个有限集合,该集合:
①为空
②由一个根节点加上两棵别称左子树和右子树组成

①二叉树不存在度大于2的结点
②二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
③对于任何的二叉树都是由以下几种情况复合而成的:空树、只有根节点、只有左子树、只有右子树、左子树右子树均存在
6.特殊的二叉树
①满二叉树:一个二叉树,如果每一层的结点都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为k,且结点总数是2^k-1,则他就是满二叉树

上图可以清晰地看出,每一层的结点数是2^(层数-1)个
第h层满了,则k层有2^(h-1)个结点
现在我们就可以推出高度为k的满二叉树的总结点数为2^h-1
假设满二叉树有N个结点,高度为h=log(N+1)
②完全二叉树:前N-1层是满的,最后一层可以不满,但是必须从左往右是连续的。要注意的是满二叉树是一种特殊的完全二叉树
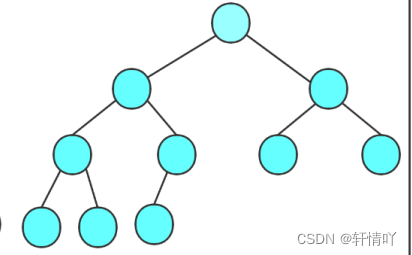
假设完全二叉树的高度为h
最多结点:也就是满二叉树2^h-1个结点
最少结点:相等于最后一层的结点数为1个,因此结果为2^(h-1)
7.二叉树的性质
①若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点
②若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1个
③对于任何一棵二叉树,如果度为0其叶结点个数为x,度为2的分支节点个数为y,则有y+1=x
④若规定根节点的层数为1,具有n个结点的满二叉树的深度为h=log(n+1)
⑤对于具有n个结点的完全二叉树,如果按照从上至下从左到右的数组顺序对所有结点从0开始编号,则对于序号为i的结点有以下的特点:
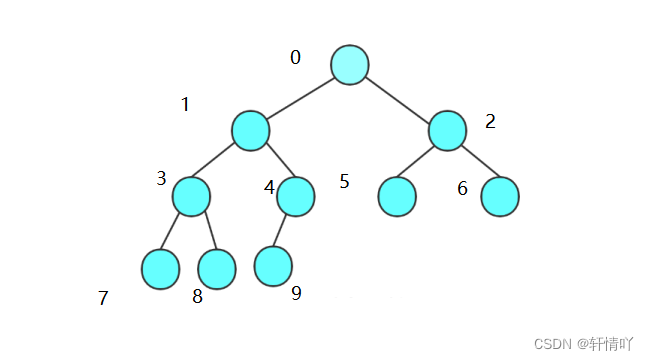
若i>0,i位置结点的双亲序号:(i-1)/2=parent;i=0,i为根节点编号,无双亲结点
设n为数组的大小,若2i+1<n,左孩子序号:2i+1=leftchild;2i+1>=n否则无左孩子
设n为数组的大小,若2i+2<n,右孩子序号:2i+2=rightchild;2i+2>=n否则无右孩子
🌸🌸二叉树(一)的知识大概就讲到这里啦,博主后续会继续更新更多数据结构的相关知识,干货满满,如果觉得博主写的还不错的话,希望各位小伙伴不要吝啬手中的三连哦!你们的支持是博主坚持创作的动力!💪💪
相关文章:

二叉树(一)
二叉树(一)1.树的概念2.树的相关概念3.树的表示4.树在实际中的运用5.二叉树概念及结构6.特殊的二叉树7.二叉树的性质🌟🌟hello,各位读者大大们你们好呀🌟🌟 🚀🚀系列专栏…...
【SCL】1200案例:天塔之光数码管显示液体混合水塔水位
使用scl编写天塔之光&数码管显示&液体混合&水塔水位 文章目录 目录 文章目录 前言 一、案例1:天塔之光 1.控制要求 2.编写程序 3.效果 二、案例2:液体混合 1.控制要求 2.编写程序 三、案例3:数码管显示 1.控制要求 2.编写程序 3…...
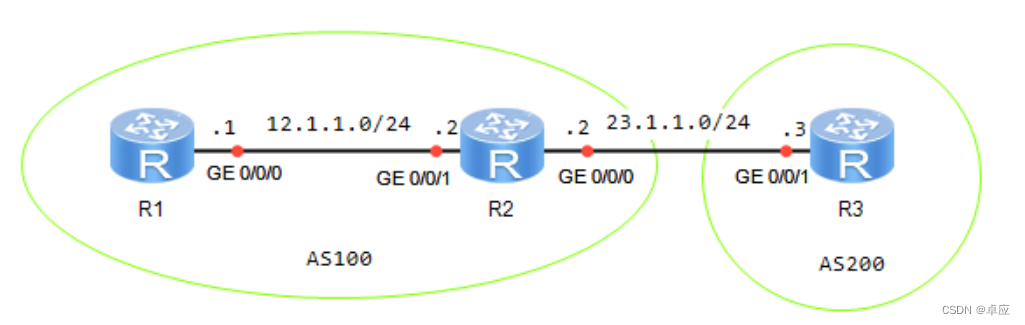
5.1配置IBGP和EBGP
5.2.1实验1:配置IBGP和EBGP 实验目的 熟悉IBGP和EBGP的应用场景掌握IBGP和EBGP的配置方法 实验拓扑 实验拓扑如图5-1所示: 图5-1:配置IBGP和EBGP 实验步骤 IP地址的配置 R1的配置 <Huawei>system-view Enter system view, return …...
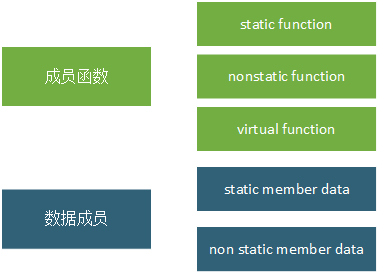
c++中超级详细的一些知识,新手快来
目录 2.文章内容简介 3.理解虚函数表 3.1.多态与虚表 3.2.使用指针访问虚表 4.对象模型概述 4.1.简单对象模型 4.2.表格驱动模型 4.3.非继承下的C对象模型 5.继承下的C对象模型 5.1.单继承 5.2.多继承 5.2.1一般的多重继承(非菱形继承) 5.2…...

[答疑]经营困难时期谈建模和伪创新-长点心和长点良心
leonll 2022-11-26 9:53 我们今年真是太难了……(此处删除若干字)……去年底就想着邀请您来给我们讲课,现在也没有实行。我想再和我们老大提,您觉得怎么说个关键理由,这样的形势合适引进UML开发流程? UML…...

计算机基础知识
计算机网络的拓扑结构 一、OSI 7层网络模型是指什么? 7层分别是什么?每层的作用是什么? OSI7层模型是 国际标准化组织(ISO)制定的一个用于计算机或通信系统间互联的标准体系。 每层功能:(自底向上) 物理层:建立、…...
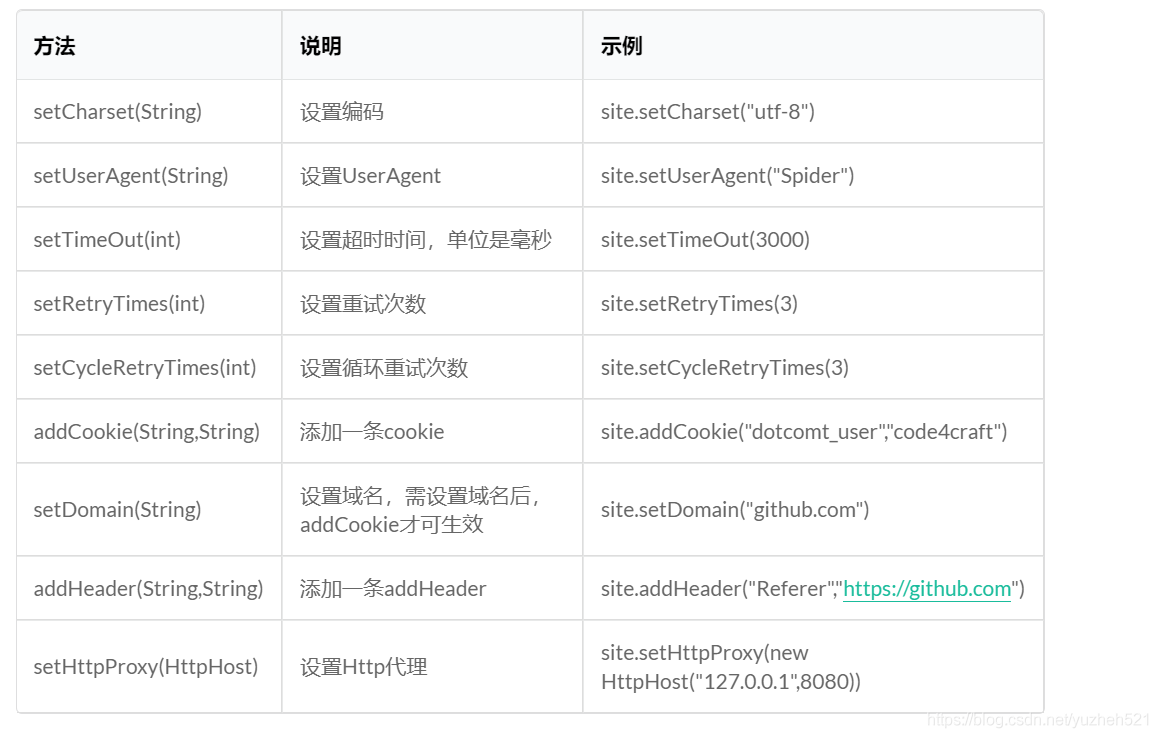
Java爬虫—WebMagic
一,WebMagic介绍WebMagic企业开发,比HttpClient和JSoup更方便一),WebMagic架构介绍WebMagic有DownLoad,PageProcessor,Schedule,Pipeline四大组件,并有Spider将他们组织起来…...

[软件工程导论(第六版)]第2章 可行性研究(复习笔记)
文章目录2.1 可行性研究的任务2.2 可行性研究过程2.3 系统流程图2.4 数据流图概念2.5 数据字典2.6 成本/效益分析2.1 可行性研究的任务 可行性研究的目的 用最小的代价在尽可能短的时间内确定问题是否能够解决。 可行性研究的3个方面 (1)技术可行性&…...
Mac下安装Tomcat以及IDEA中的配置
安装brew 打开终端输入以下命令: /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)" 搜索tomcat版本,输入以下命令: brew search tomcat 安装自己想要的版本,例…...
【Linux详解】——文件基础(I/O、文件描述符、重定向、缓冲区)
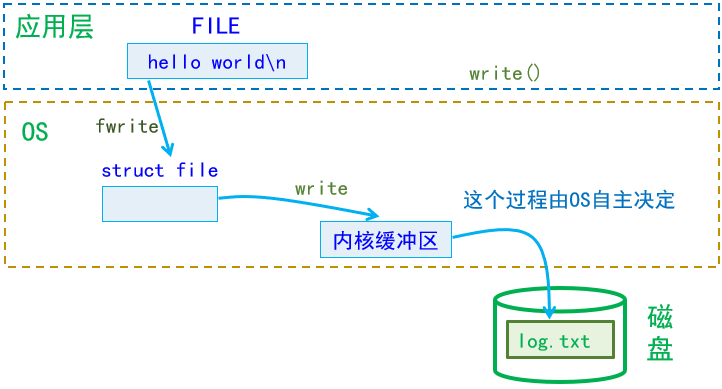
📖 前言:本期介绍文件基础I/O。 目录🕒 1. 文件回顾🕘 1.1 基本概念🕘 1.2 C语言文件操作🕤 1.2.1 概述🕤 1.2.2 实操🕤 1.2.3 OS接口open的使用(比特位标记)…...

HomMat2d
1.affine_trans_region(区域的任意变换) 2.hom_mat2d_identity(创建二位变换矩阵) 3.hom_mat2d_translate(平移) 4.hom_mat2d_scale(缩放) 5.hom_mat2d_rotate(旋转 &…...
Python3 JSON 数据解析
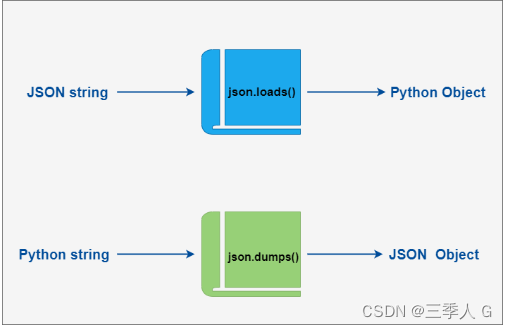
Python3 JSON 数据解析 JSON (JavaScript Object Notation) 是一种轻量级的数据交换格式。 Python3 中可以使用 json 模块来对 JSON 数据进行编解码,它包含了两个函数: json.dumps(): 对数据进行编码。json.loads(): 对数据进行解码。 在 json 的编解码…...
Homebrew 安装遇到的问题
Homebrew 安装遇到的问题 例如:第一章 Python 机器学习入门之pandas的使用 文章目录Homebrew 安装遇到的问题前言一、安装二、遇到的问题1.提示 zsh: command not found: brew三、解决问题前言 使用 Homebrew 能够 安装 Apple(或您的 Linux 系统&#…...

Metasploit框架基础(二)
文章目录前言一、Meatsplooit的架构二、目录结构datadocumentationlibmodulesplugins三、Measploit模块四、Metasploit的使用前言 Metasploit是用ruby语言开发的,所以你打开软件目录,会发现很多.rb结尾的文件。ruby是一门OOP的语言。 一、Meatsplooit的…...

c++容器
1、vector容器 1.1性质 a)该容器的数据结构和数组相似,被称为单端数组。 b)在存储数据时不是在原有空间上往后拓展,而是找到一个新的空间,将原数据深拷贝到新空间,释放原空间。该过程被称为动态拓展。 vec…...

Vue.js如何实现对一千张图片进行分页加载?
目录 vue处理一千张图片进行分页加载 分页加载、懒加载---概念介绍: 思路: 开发过程中,如果后端一次性返回你1000多条图片或数据,那我们前端应该怎么用什么思路去更好的渲染呢? 第一种:我们可以使用分页…...
)
计算机网络复习(六)
考点:MIME及其编码(base64,quoted-printable)网络协议http是基于什么协议,应用层到网络层基于什么协议6-27.试将数据 11001100 10000001 00111000 进行 base64 编码,并得到最后传输的 ASCII 数据。答:先将 24 比特的二…...

Redis进阶:布隆过滤器(Bloom Filter)及误判率数学推导
1 缘起 有一次偶然间听到有同事在说某个项目中使用了布隆过滤器, 哎呦,我去,我竟然不知道啥是布隆过滤器, 这我哪能忍?其实,也可以忍,但是,可能有的面试官不能忍!&#…...
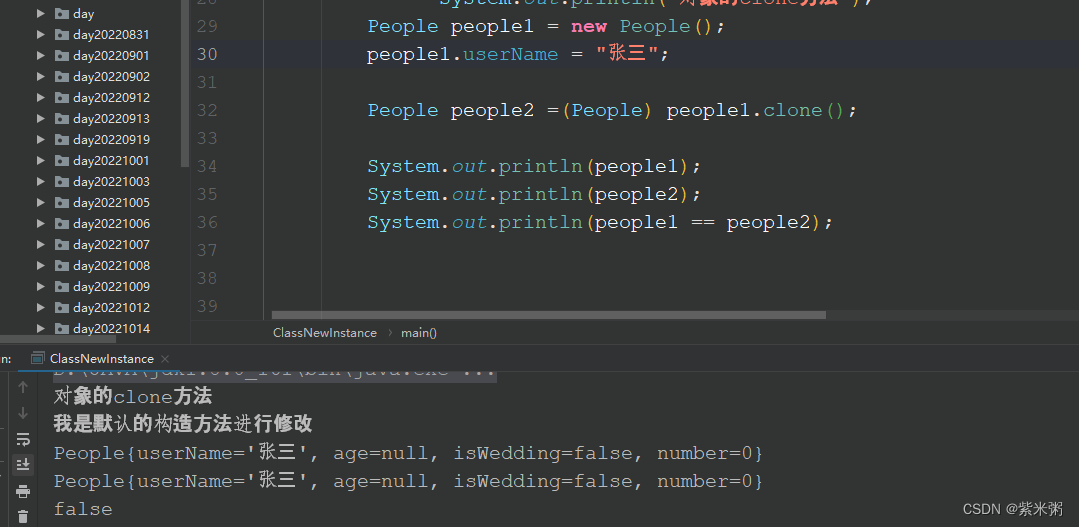
Java创建对象的方式
Java创建对象的五种方式: (1)使用new关键字 (2)使用Object类的clone方法 (3)使用Class类的newInstance方法 (4)使用Constructor类中的newInstance方法 (5&am…...

dom基本操作
1、style修改样式 基本语法: 元素.style.样式’值‘ 注意: 1.修改样式通过style属性引出 2.如果属性有-连接符,需要转换为小驼峰命名法 3.赋值的时候,需要的时候不要忘记加css单位 4.后面的值必须是字符串 <div></div> // 1、…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
