【左神算法刷题班】第16节:累加和为k的数组、逆序对问题、约瑟夫环问题
题目1
给定一个有正、有负、有0的数组arr,
给定一个整数k,
返回arr的子集是否能累加出k
1)正常怎么做?
2)如果arr中的数值很大,但是arr的长度不大,怎么做?
问题 1)思路
如果数组中只有正数,那么这就是一个普通的背包问题,
递归函数用 process(i,j) 表示从0到i随便选,能否选出累加和为j的数字。
在 process 内部,可以选i,或者不选i。
- 如果不选 i,就看 process(i-1, j) 是否返回 true
- 如果选 i,就看 process(i-1, j-arr[i]) 是否返回 true
将递归转换成 dp,就是dp[i][j]表示从0到i随便选,能否选出累加和为j的数字。
dp 表的难点在于,数组中有负数,需要将下标做一个平移。
问题 2)思路
我的思路是,当 arr 数值很大的时候,可以用 暴力递归 + HashMap 来做缓存表,这样只需要计算那些用得到的结果,而不需要写满整个 arr 数据范围的结果。
左神的思路是,假设 arr 的长度是 40,用分治,左边 20 个数用暴力算出所有可能的累加和(2^20=1048576),右边也得到 1048576 个结果。(一般都是二分之后再整合,你要分成三部分也可以,但整合的时候就会复杂一些)
如果单独用左部分,或者单独用右部分,就能够得到目标累加和的话,直接返回就可以了。如果不行,要考虑左右合并的情况。
题目2
给定一个正数数组arr,
返回arr的子集“不能累加出的“最小正数
1)正常怎么做?
2)如果arr中肯定有1这个值,怎么做?
问题 1)思路
和题目 1 很像,而且所有的数都是正数,可以看成是一个普通的背包问题。
process(i,j) 表示从0到i随便选,能否选出累加和为j的数字。
在 process 内部,可以选i,或者不选i。
- 如果不选 i,就看 process(i-1, j) 是否返回 true
- 如果选 i,就看 process(i-1, j-arr[i]) 是否返回 true
最后从 j=1 开始 j++,一直找到第一个 process(i, j) 返回为 false 的 j,就是最终结果。
问题 2)思路
其实 问题1)的最优思路就是,如果没有 1,则返回答案 1。如果有 1,则用下面的思路。
先排序,排序后,左边第 0 位置一定是 1。
定义变量 range=1,含义为,从 1-range 范围上的正数都能累加出来。下面我们来分析 range 的扩充条件:
如果 1 位置的数还是 1,则 range 变成 2。
如果 2 位置的数是 2,则 range 变成 4。
普遍的,我来到 i 位置发现 arr[i]=17,range=100,代表从 0 到 i-1 位置能够得到 1~100 里的所有数,由此可以推断,加上 i 位置之后,可以得到 1~117 所有的数。
普遍的,我来到 i 位置发现 arr[i]=101,range=100,代表从 0 到 i-1 位置能够得到 1~100 里的所有数,由此可以推断,加上 i 位置之后,可以得到 1~201 所有的数。
但,普遍的,我来到 i 位置发现 arr[i]=102,range=100,代表从 0 到 i-1 位置能够得到 1~100 里的所有数,但以后怎么也得不到 101 了。
所以,range 扩充的条件是:
- 如果 arr[i] > range+1,那么以后就再也得不到 range+1 的累加和了,直接返回 range+1
- 否则,range 可以扩充为 range + arr[i]
题目3
Leetcode原题:
https://leetcode.com/problems/patching-array/
思路
我们先举一个极端的例子,假设 nums 为空,n=1000,我们想要生成从 1~1000 之间所有的数。
思路和题目2很像。用 range 表示当前能够得到的最大累加和。
首先我肯定需要 1,这样就能得到 [1,1] 区间所有的数,range = 1。
然后我需要 2,就可以得到 [1, 1+2] 区间所有的数,range = 3。
然后我需要 4,就可以得到 [1, 3+4] 区间所有的数,range = 7。
然后我需要 8,…
然后,我们忘掉前面的例子,举一个普遍的例子。
假设 nums=[4, 5, 17, 39],n=83
首先我们来看 nums 中的第一个数字 4,我们要先能够得到 4 之前所有的数字,所以根据前面的分析,需要加入 1,2,得到 range=7
在此基础上,来到 nums 中的第二个数字 5,更新range为 7+5=12
在此基础上,来到 nums 中的第三个数字 17,不能直接更新 range,需要想办法得到 13 14 15 16。所以需要加入 range+1 = 13,并且更新 range 为 12+13=25。然后用 17 更新 range=25+17=42
在此基础上,来到 nums 中的第四个数字39,更新range为42+39=81
整个数组遍历结束了,而最终目标83还有距离,所以需要再补一个range+1=82,就能得到1~83范围内所有的数字。
题目4
给定整数power,给定一个数组arr,给定一个数组reverse,含义如下:
arr的长度一定是2的power次方
reverse中的每个值一定都在0~power范围。
例如power = 2, arr = {3, 1, 4, 2},reverse = {0, 1, 0, 2}
任何一个在前的数字可以和任何一个在后的数组,构成一对数
可能是升序关系、相等关系或者降序关系
比如arr开始时有如下的降序对:(3,1)、(3,2)、(4,2),一共3个
接下来根据reverse对arr进行调整:
reverse[0] = 0, 表示在arr中,划分每1(2的0次方)个数一组,然后每个小组内部逆序,那么arr变成[3,1,4,2],此时有3个逆序对
reverse[1] = 1, 表示在arr中,划分每2(2的1次方)个数一组,然后每个小组内部逆序,那么arr变成[1,3,2,4],此时有1个逆序对
reverse[2] = 0, 表示在arr中,划分每1(2的0次方)个数一组,然后每个小组内部逆序,那么arr变成[1,3,2,4],此时有1个逆序对
reverse[3] = 2, 表示在arr中,划分每4(2的2次方)个数一组,然后每个小组内部逆序,那么arr变成[4,2,3,1],此时有4个逆序对
所以返回[3,1,1,4],表示每次调整之后的逆序对数量
输入数据状况:
power的范围[0,20]
arr长度范围[1,10的7次方]
reverse长度范围[1,10的6次方]
思路
假设我们有 8 个数,arr = [2 1 7 5 3 4 6 8]
当以 2 个数为一组的时候,我们假设每个组内逆序对的个数之和是 a,正序对个数之和是 b
注意,每一个组内的逆序对,第一个数要来自组内左侧,第二个数要来自组内右侧。
这样,在每个组中逆序对相加,求总的逆序对数量的时候,才不会重复计算。2个一组的时候,[2 | 1] [7 | 5] [3 | 4] [6 | 8]
其中,正序对包括 (3,4),(6,8),正序对个数为2.
其中,逆序对包括 (2,1),(7,5),逆序对个数为2.4个一组的时候,[2 1 | 7 5][3 4 | 6 8]
其中,正序对包括 (2,7),(2,5),(1,7),(1,5),(3,6),(3,8),(4,6),(4,8),正序对个数为8.
其中,逆序对没有,逆序对个数为08个一组的时候,[2 1 7 5 | 3 4 6 8]
其中,正序对包括 (2,3),(2,4),(2,6),(2,8),(1,3),(1,4),(1,6),(1,8),(7,8),(5,6),(5,8),正序对个数为11.
其中,逆序对包括 (7,3),(7,4),(7,6),(5,3),(5,4),逆序对个数为5同样的,我们假设 4(2的2次方)个一组的时候,逆序对的个数为 c,正序对个数之和是 d.
同样的,我们假设 8(2的3次方)个一组的时候,逆序对的个数为 e,正序对个数之和是 f.
我们把上面的假设总结成表格:
| 几个数一组 | 逆序对的个数 | 正序对的个数 |
|---|---|---|
| 2(2的1次方) | a | b |
| 4(2的2次方) | c | d |
| 8(2的3次方) | e | f |
当我们将“ 4(2的2次方)个数字组成的小组”内部逆序的时候,它只影响“2(2的1次方)个数字一组”的小组,和“4(2的2次方)个数字一组的小组”,不会影响“8(2的3次方)一组的小组”。逆序后,表格变成如下:
| 几个数一组 | 逆序对的个数 | 正序对的个数 |
|---|---|---|
| 2(2的1次方) | b(左右交换) | a(左右交换) |
| 4(2的2次方) | d(左右交换) | c(左右交换) |
| 8(2的3次方) | e(不变) | f(不变) |
普遍的,当我们要逆序“2的n次方个数字组成的小组”的时候,表格中,“2的n次方一组的小组”这一行下面的所有小组,都不会被影响。这一行上面的所有小组(包括自身),正序对个数和逆序对个数发生交换。
这样,每一次组内做逆序的时候,就可以非常快速的计算逆序之后的逆序对数量。
那么,怎么拥有一开始的表格信息?用归并排序来算。去看体系学习班第4节和第5节,是和merge sort有关的题目。
题目5
约瑟夫环问题
给定一个链表头节点head,和一个正数m
从头开始,每次数到m就杀死当前节点
然后被杀节点的下一个节点从1开始重新数,
周而复始直到只剩一个节点,返回最后的节点
Leetcode :
https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/
相关文章:

【左神算法刷题班】第16节:累加和为k的数组、逆序对问题、约瑟夫环问题
题目1 给定一个有正、有负、有0的数组arr, 给定一个整数k, 返回arr的子集是否能累加出k 1)正常怎么做? 2)如果arr中的数值很大,但是arr的长度不大,怎么做? 问题 1)…...

【React | 前端】在React的前端页面中,判断某个变量值是否被定义?根据是否定义显示不同的内容?
问题描述 在React的前端页面中,判断某个变量值是否被定义?根据是否定义显示不同的内容? 问题场景 假如,现在有一个需求是设计一个新功能,新功能中要求新增一个之前没有的变量,假设是计算某一个数组的长度…...
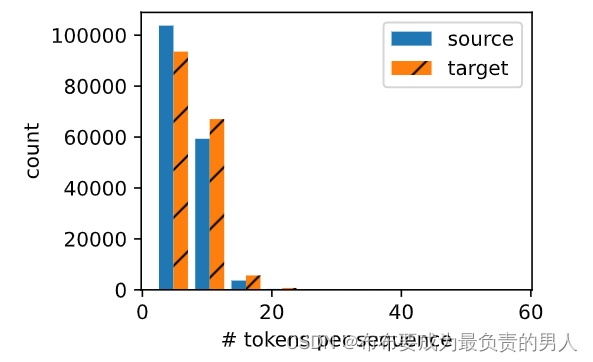
机器学习深度学习——seq2seq实现机器翻译(数据集处理)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——从编码器-解码器架构到seq2seq(机器翻译) 📚订阅专栏:机…...
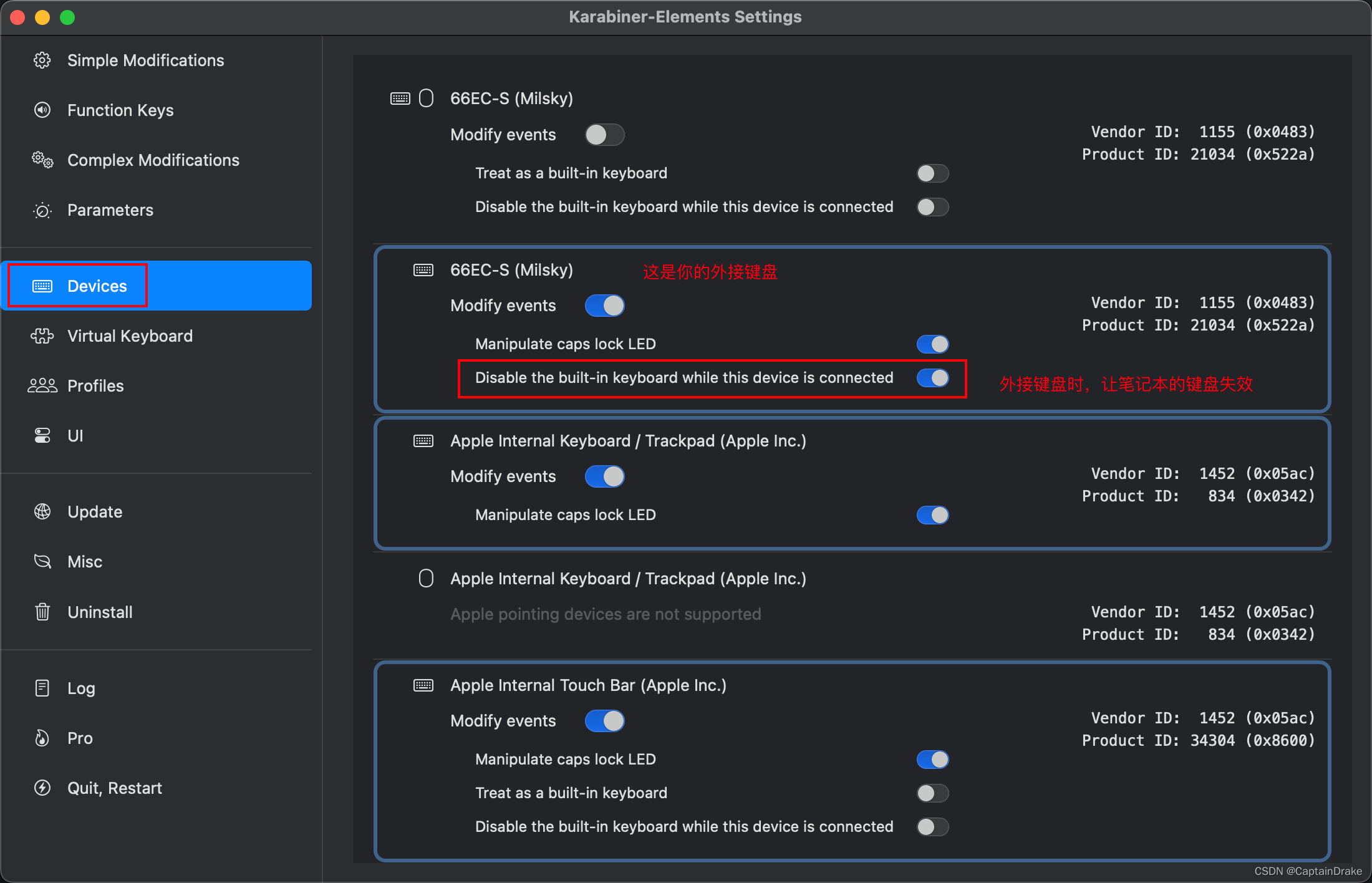
锁定Mac的内置键盘,防止外接键盘时的误触
场景:把你的外接键盘放在mac上,然后打字时,发现外接键盘误触mac键盘,导致使用体验极差 解决方案:下载Karabiner-Elements这款软件,并给它开启相关权限。 地址:https://github.com/pqrs-org/Ka…...
由于找不到d3dx9_42.dll,无法继续执行代码。重新安装程序可能会解决此问题
d3dx9_42.dll是一个动态链接库文件,它是Microsoft DirectX 9的一部分。这个文件包含了DirectX 9的一些函数和资源,用于支持计算机上运行基于DirectX 9的应用程序和游戏。它通常用于提供图形、音频和输入设备的支持,以及其他与图形和游戏相关的…...

解决Vue+Element UI使用el-dropdown(下拉菜单)国际化时菜单label信息没有刷新的情况
说明:该篇博客是博主一字一码编写的,实属不易,请尊重原创,谢谢大家! 问题描述 在默认中文时,点击布局大小下拉菜单正常显示中文,此时切换至英文时,再次点击下拉菜单,还…...

Prometheus技术文档-概念
Prometheus是一个开源的项目连接如下: Prometheus首页、文档和下载 - 服务监控系统 - OSCHINA - 中文开源技术交流社区 基本概念: Prometheus是一个开源的系统监控和告警系统,由Google的BorgMon监控系统发展而来。它主要用于监控和度量各种…...
是否选中和获取选中值方法总结)
JQuery判断radio(单选框)是否选中和获取选中值方法总结
使用checked属性判断选中、jquery获取radio单选按钮的值、获取一组radio被选中项的值、设置单选按钮被选中等,详细如下: 一、利用获取选中值判断选中 <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.…...

Effective Python 读书笔记
文章目录 前言第1章:用Pythonic方式来思考 1. 用Pythonic方式来思考 2. 遵循PEP8风格3. 了解bytes, str, unicode区别4. 用辅助函数取代复杂表达式5. 了解切割序列的方法6. 单次切片操作内,不要同时指定start, end, stride 7. 用列表推导取代map, filter…...
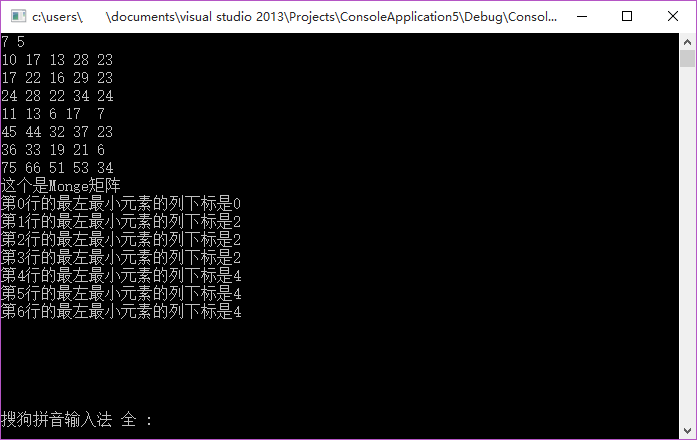
Monge矩阵
Monge矩阵 对一个m*n的实数矩阵A,如果对所有i,j,k和l,1≤ i<k ≤ m和1≤ j<l ≤ n,有 A[i,j]A[k,l] ≤ A[i,l]A[k,j] 那么,此矩阵A为Monge矩阵。 换句话说,每当我们从矩阵中挑…...
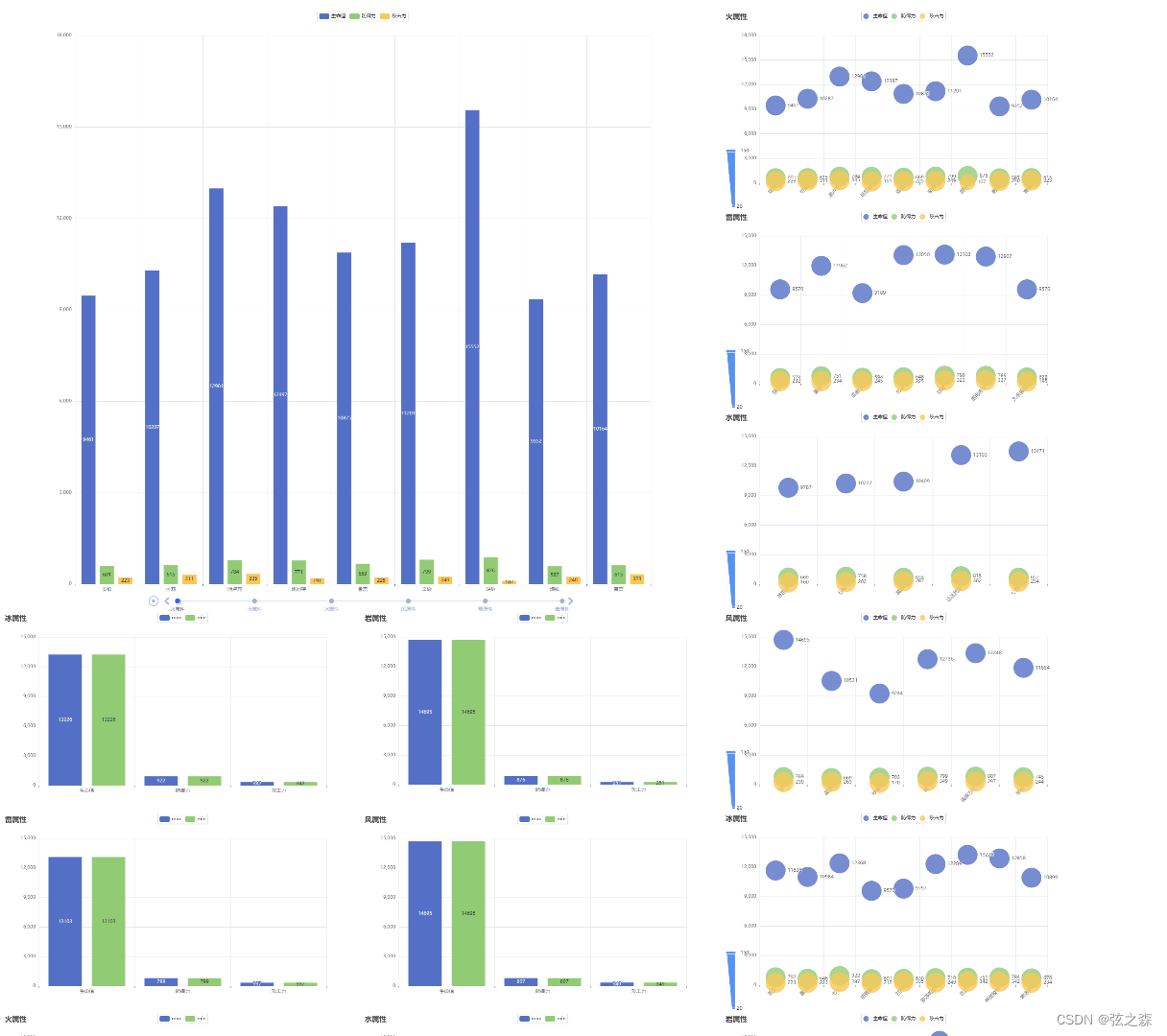
(5)所有角色数据分析页面的构建-5
所有角色数据分析页面,包括一个时间轴柱状图、六个散点图、六个柱状图(每个属性角色的生命值/防御力/攻击力的max与min的对比)。 """绘图""" from pyecharts.charts import Timeline from find_type import FindType import pandas …...
:专利撰写资料汇总)
专利进阶(三):专利撰写资料汇总
文章目录 一、前言二、资料汇总三、拓展阅读 一、前言 在专利撰写前,需要首先了解专利撰写所需遵守的基本规则。可以借助的撰写工具是什么。文献检索在哪里?注意事项是什么?本篇博文会就以上问题进行逐一解答。 专利撰写基本原则࿱…...

maven编译始终提示无效的目标发行版的解决方法
摘自个人印象笔记2021-05-07:https://app.yinxiang.com/fx/55e1d5f4-aeea-446a-a768-0f1a48195f5b(图显示不完整可查看原笔记内容)1:确保IDE中的编译版本正确 在idea中,主要看项目属性中和setting的java compiler中对应的jdk版本是否正确&…...

系统架构设计高级技能 · 软件可靠性分析与设计(三)【系统架构设计师】
系列文章目录 系统架构设计高级技能 软件架构概念、架构风格、ABSD、架构复用、DSSA(一)【系统架构设计师】 系统架构设计高级技能 系统质量属性与架构评估(二)【系统架构设计师】 系统架构设计高级技能 软件可靠性分析与设计…...
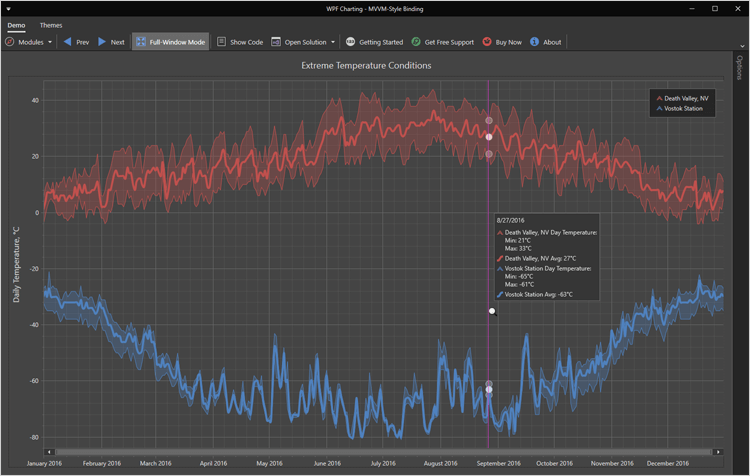
界面控件DevExpress WPF Chart组件——拥有超快的数据可视化库!
DevExpress WPF Chart组件拥有超大的可视化数据集,并提供交互式仪表板与高性能WPF图表库。DevExpress Charts提供了全面的2D / 3D图形集合,包括数十个UI定制和数据分析/数据挖掘选项。 PS:DevExpress WPF拥有120个控件和库,将帮助…...

【网络安全】等保测评安全物理环境
【网络安全】等保测评&安全物理环境 前言第1章 安全物理环境1.1 物理位置选择1.2 物理访问控制(高风险项)1.3 防盗窃1.4 防雷击1.5 防火1.6 防水防潮1.7 防静电1.8 温湿度控制1.9 电力供应1.10 电磁防护 前言 等级保护对象是由计算机或其他信息终端…...
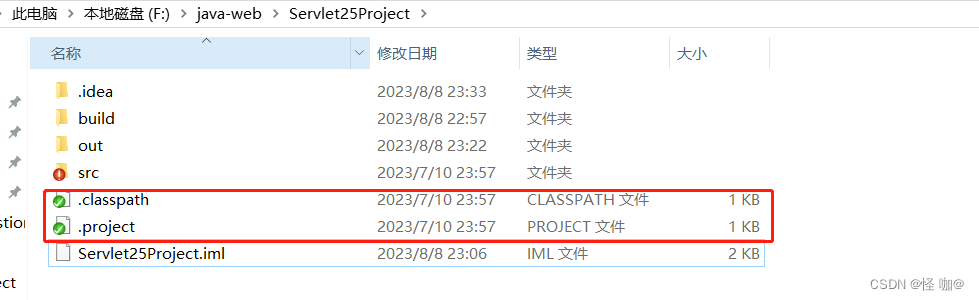
Intellij IDEA 导入 eclipse web 项目详细操作
Eclipse当中的web项目都会有这两个文件。但是idea当中应该是没有的,所以导入会出现兼容问题。但是本篇文章会教大家如何导入,并且导入过后还能使用tomcat运行。文章尽可能以图片的形式进行演示。我的idea使用的版本是2022.3.3版本。当然按正常来说版本之…...

安卓java A应用切换到B应用,来回切换不执行OnCreate
需求:安卓java如何做到A应用切换到B应用,如果B应用没启动就启动,如果B应用已经启动就仅仅切换到B应用。B应用再切换回A应用,不要重复执行OnCreate! 在 A 应用中的: 在 A 应用中,如果你希望在切换回 B 应用…...

【Linux】批量恢复文件权限
批量恢复文件权限 Linux 中,如果意外误操作将根目录目录权限批量设置,比如 chmod -R 777 / ,系统中的大部分服务以及命令将无法使用,这时候可以通过系统自带的 getfacl 命令来拷贝和还原系统权限,若是其他系统目录被误…...
数据可视化(八)堆叠图,双y轴,热力图
1.双y轴绘制 #双Y轴可视化数据分析图表 #add_subplot() dfpd.read_excel(mrbook.xlsx) x[i for i in range(1,7)] y1df[销量] y2df[rate] #用来正常显示负号 plt.rcParams[axes.unicode_minus]False figplt.figure() ax1fig.add_subplot(1,1,1)#一行一列,第一个区域…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
