《3D 数学基础》12 几何图元
目录
1 表达图元的方法
1.1 隐式表示法
1.2 参数表示
1.3 直接表示
2. 直线和射线
2.1 射线的不同表示法
2.1.1 两点表示
2.1.2 参数表示
2.1.3 相互转换
2.2 直线的不同表示法
2.2.1 隐式表示法
2.2.2 斜截式
2.2.3 相互转换
3. 球
3.1 隐式表示
1 表达图元的方法
1.1 隐式表示法
定义一个布尔函数f(x,y,z),点在图元上,则布尔函数为真,否则为假。例如
1.2 参数表示
t从0-1变化,点(x(t), y(t))的轨迹就是所描述的图元,上面描述的是中心在原点的单位圆。
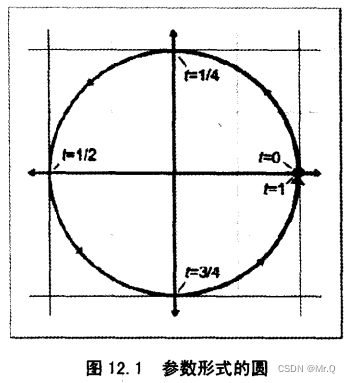
t有时的变换范围是0-L,L是图元的长度。上面的函数只有一个参数,是单变量,其轨迹是一个曲线,如果是两个变量,其轨迹是曲面。
1.3 直接表示
直接体现图元的本质信息。例如线段:两个端点表示;球:球心和半径表示。
2. 直线和射线
经典定义

书中对射线定义做了修改:有向线段。

2.1 射线的不同表示法
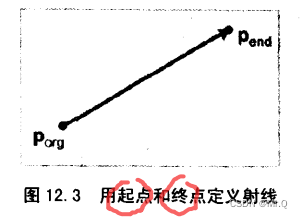
2.1.1 两点表示
两个端点p_org和p_end
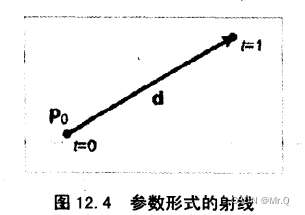
2.1.2 参数表示
或者
起点坐标是p(0)=p_0, 终点坐标是p(1)=p_0 + d,p_0 (即p_org)指定了了射线的位置信息,向量d指定了长度和方向(d = p_end - p_org = (dx, dy))。
2.1.3 相互转换
两点形式 -> 参数形式
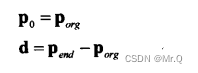
参数形式 -> 两点形式
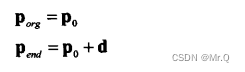
2.2 直线的不同表示法
2.2.1 隐式表示法

记向量n=[a, b], p是线上任意一点,d是标量,则向量记法的隐式表示法

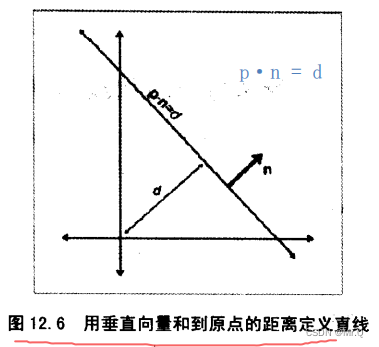
其中向量n转换成单位向量:
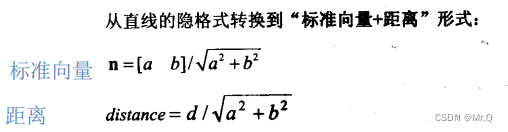
转换:射线( d = (dx, dy), p_org = (p_orgx, p_orgy) )所在的隐式表示直线
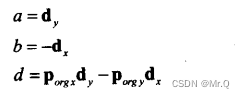
2.2.2 斜截式
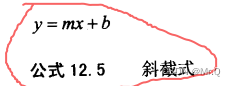

2.2.3 相互转换
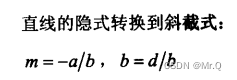
其中隐式ax+by=d, 令x=0,则截距y=d/b.
3. 球
3.1 隐式表示

到球心c的距离为给定距离r的点的集合,p为球面上点。隐式表示:
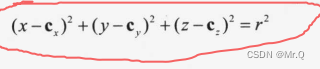
相关文章:
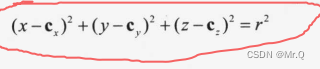
《3D 数学基础》12 几何图元
目录 1 表达图元的方法 1.1 隐式表示法 1.2 参数表示 1.3 直接表示 2. 直线和射线 2.1 射线的不同表示法 2.1.1 两点表示 2.1.2 参数表示 2.1.3 相互转换 2.2 直线的不同表示法 2.2.1 隐式表示法 2.2.2 斜截式 2.2.3 相互转换 3. 球 3.1 隐式表示 1 表达图元的方…...
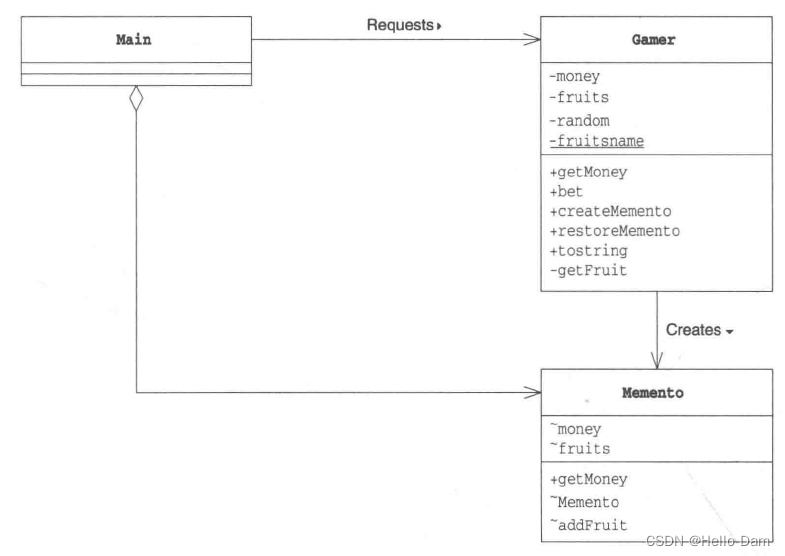
【设计模式——学习笔记】23种设计模式——备忘录模式Memento(原理讲解+应用场景介绍+案例介绍+Java代码实现)
案例引入 游戏角色有攻击力和防御力,在大战Boss前保存自身的状态(攻击力和防御力),当大战Boss后攻击力和防御力下降,可以从备忘录对象恢复到大战前的状态 传统设计方案 针对每一种角色,设计一个类来存储该角色的状态 【分析】…...
致谢丨感谢有你,JumpServer开源项目九周年致谢名单
2014年到2023年,JumpServer开源项目已经走过了九年的时间。感谢以下社区贡献者对JumpServer项目的帮助和支持。 因为有你,一切才能成真。 JumpServer开源项目贡献者奖杯将于近日邮寄到以上贡献者手中,同时JumpServer开源项目组还准备了一份小…...
使用 Python 和 Flask 构建简单的 Restful API 第 1 部分
一、说明 我将把这个系列分成 3 或 4 篇文章。在本系列的最后,您将了解使用flask构建 restful API 是多么容易。在本文中,我们将设置环境并创建将显示“Hello World”的终结点。 我假设你的电脑上安装了python 2.7和pip。我已经在python 2.7上测试了本文…...
)
【深度学习所有损失函数】在 NumPy、TensorFlow 和 PyTorch 中实现(2/2)
一、说明 在本文中,讨论了深度学习中使用的所有常见损失函数,并在NumPy,PyTorch和TensorFlow中实现了它们。 (二-五)见 六、稀疏分类交叉熵损失 稀疏分类交叉熵损失类似于分类交叉熵损失,但在真实标签作为整数而不是独热编码提…...

Hazel 引擎学习笔记
目录 Hazel 引擎学习笔记学习方法思考引擎结构创建工程程序入口点日志系统Premake\MD没有 cpp 文件的项目会出错include 到某个库就要包含这个库的路径,注意头文件展开 事件系统 获取和利用派生类信息预编译头文件抽象窗口类和 GLFWgit submodule addpremake 脚本禁…...
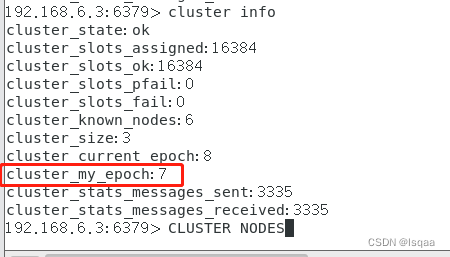
Linux系统下Redis3.2集群
本节主要学习reids主从复制的概念,作用,缺点,流程,搭建,验证,reids哨兵模式的概念,作用,缺点,结构,搭建,验证等。 文章目录 一、redis主从复制 …...
Android图形-合成与显示-SurfaceTestDemo
目录 引言: 主程序代码: 结果呈现: 小结: 引言: 通过一个最简单的测试程序直观Android系统的native层Surface的渲染显示过程。 主程序代码: #include <cutils/memory.h> #include <utils/L…...

高压放大器怎么设计(高压放大器设计方案)
高压放大器是一种用于将低电压信号转换成高电压信号的电子设备,广泛应用于通信、雷达、医疗设备等领域。在设计高压放大器时,需要考虑多种因素,如输入输出信号的特性、电路结构的选择、电源和负载匹配等。本文将介绍高压放大器的设计方法和注…...

SpringBoot yml配置注入
yaml语法学习 1、配置文件 SpringBoot使用一个全局的配置文件 , 配置文件名称是固定的 application.properties 语法结构 :keyvalue application.yml 语法结构 :key:空格 value 配置文件的作用:修改SpringBoot自动…...

中科亿海微乘法器(LPMMULT)
引言 FPGA(可编程逻辑门阵列)是一种可在硬件级别上重新配置的集成电路。它具有灵活性和可重构性,使其成为处理各种应用的理想选择,包括数字信号处理、图像处理、通信、嵌入式系统等。在FPGA中,乘法器是一种重要的硬件资…...
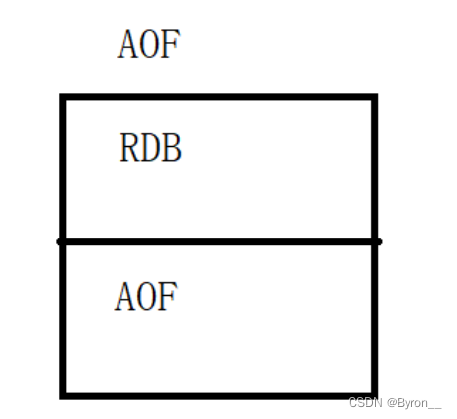
Redis_持久化(AOF、RDB)
6. Redis AOF 6.1 简介 目前,redis的持久化主要应用AOF(Append Only File)和RDF两大机制,AOF以日志的形式来记录每个写操作(增量保存),将redis执行过的所有指令全部安全记录下来(读…...
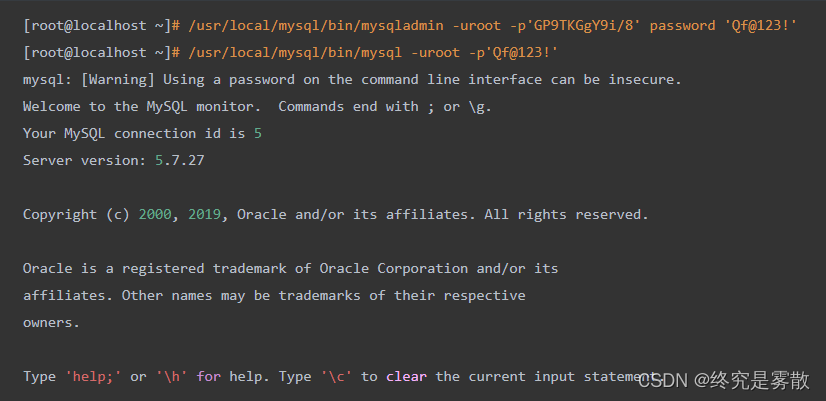
开源数据库Mysql_DBA运维实战 (部署服务篇)
前言❀ 1.数据库能做什么 2.数据库的由来 数据库的系统结构❀ 1.数据库系统DBS 2.SQL语言(结构化查询语言) 3.数据访问技术 部署Mysql❀ 1.通过rpm安装部署Mysql 2.通过源码包安装部署Mysql 前言❀ 1.数据库能做什么 a.不论是淘宝,吃鸡,爱奇艺…...
【Java学习】System.Console使用
背景 在自学《Java核心技术卷1》的过程中看到了对System.Console的介绍,编写下列测试代码, public class ConsoleTest {public static void main(String[] args) {Console cs System.console();String name cs.readLine("AccountInfo: ");…...

从零学算法154
154.已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,4,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4] 若旋转 7 次&#…...

95 | Python 设计模式 —— 策略模式
策略模式(Strategy Pattern) 引言 策略模式是一种行为型设计模式,它定义了一系列的算法,并将每个算法封装在独立的策略类中,使得这些算法可以相互替换,而不影响客户端的使用。策略模式可以让客户端根据不同的需求选择不同的算法,从而使得系统更加灵活和可扩展。 在本…...
)
【BASH】回顾与知识点梳理(十九)
【BASH】回顾与知识点梳理 十九 十九. 循环 (loop)19.1 while do done, until do done (不定循环)19.2 for...do...done (固定循环)19.3 for...do...done 的数值处理(C写法)19.4 搭配随机数与数组的实验19.5 shell script 的追踪与 debug19.6 what_to_eat-2.sh debug结果解析 该…...
Selenium之css怎么实现元素定位?
世界上最远的距离大概就是明明看到一个页面元素站在那里,但是我却定位不到!! Selenium定位元素的方法有很多种,像是通过id、name、class_name、tag_name、link_text等等,但是这些方法局限性太大, 随着自动…...
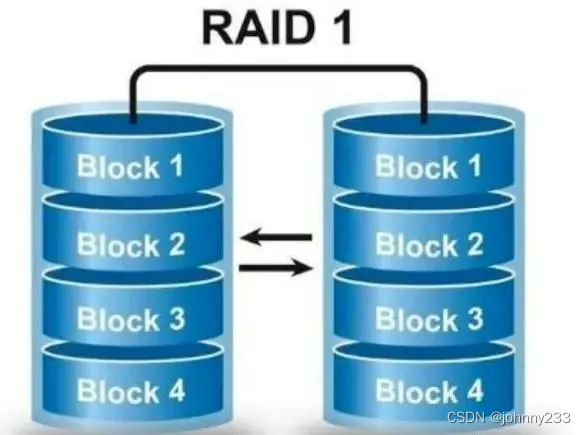
计算机基础之RAID技术
概述 RAID,Redundant Array of Independent Disks,独立磁盘冗余阵列,一种把多块独立的硬盘(物理硬盘)按不同的方式组合起来形成一个硬盘组(逻辑硬盘),从而提供比单个硬盘更高的存储…...

辽宁线上3D三维虚拟工厂生产仿真系统应用场景及优势
工厂虚拟仿真是一种基于计算机技术和虚拟现实技术的数字化解决方案,它可以通过模拟工厂中的设备、流程和操作,来为工程师和操作人员提供了一个沉浸式的虚拟环境,帮助他们更好地了解和优化工厂生产过程。 工厂VR三维可视化技术为工业生产提供了…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
