数学建模学习(9):模拟退火算法
模拟退火算法(Simulated Annealing, SA)的思想借 鉴于固体的退火原理,当固体的温度很高的时候,内能比
较大,固体的内部粒子处于快速无序运动,当温度慢慢降 低的过程中,固体的内能减小,粒子的慢慢趋于有序,最
终,当固体处于常温时,内能达到最小,此时,粒子最为 稳定。模拟退火算法便是基于这样的原理设计而成。
 模拟退火算法过程
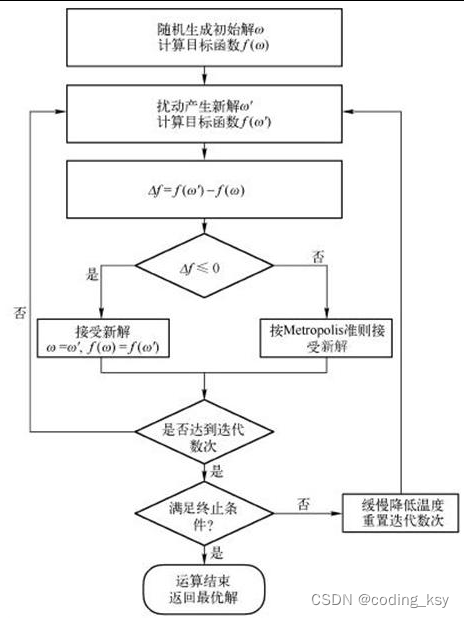
模拟退火算法过程
(1)随机挑选一个单元k,并给它一个随机的位移,求出系统因此而产生的能
量变化ΔEk。
(2)若ΔEk⩽ 0,该位移可采纳,而变化后的系统状态可作为下次变化的起点;
若ΔEk>0,位移后的状态可采纳的概率为
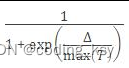
式中T为温度,然后从(0,1)区间均匀分布的随机数中挑选一个数R,若R<Pk,
则将变化后的状态作为下次的起点;否则,将变化前的状态作为下次的起点。
(3)转第(1)步继续执行,知道达到平衡状态为止。
利用模拟退火算法工具箱求解问题:
%%
clc;clear;
%%普通的目标函数
fun = @dejong5fcn %目标函数
%[x,fval] = simulannealbnd(fun,[0,0])%[0,0]凭经验猜测的初始值,没有的话,随意写就行
options = saoptimset('PlotFcns',{@saplotbestx,@saplotbestf,@saplotx,@saplotf})
x0 = [0,0];
lb = [-64,-64];%下限
ub = [64,64];%下限
[x,fval] = simulannealbnd(fun,x0,lb,ub,options);
%%
求:
% min f(x) = (4 - 2.1*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-4 + 4*x2^2)*x2^2;
% 写成函数形式
% function y = simple_objective(x)
% y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
%%
fun = @simple_objective;%注意需要将其放在最前面
X0 = [0.5 0.5]; % 初始点
lb = [-64 -64];
ub = [64 64];
[x,fval,exitFlag,output] = simulannealbnd(fun,X0,lb,ub);
fprintf('The number of iterations was : %d\n', output.iterations);
fprintf('The number of function evaluations was : %d\n', output.funccount);
fprintf('The best function value found was : %g\n', fval);
%%% 求:
% min f(x) = (a - b*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-c + c*x2^2)*x2^2;
%
% 写成函数形式
% function y = parameterized_objective(x,a,b,c)
% y = (a - b*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-c + c*x(2)^2)*x(2)^2;
%%带有常数的目标函数
a = 4; b = 2.1; c = 4; % define constant values
fun = @(x) parameterized_objective(x,a,b,c);
X0 = [0.5 0.5];
options = saoptimset('PlotFcns',{@saplotbestx,@saplotbestf,@saplotx,@saplotf})
[x,fval] = simulannealbnd(fun,X0,options)
%自定义目标函数1
function y = parameterized_objective(x,a,b,c)y = (a - b*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-c + c*x(2)^2)*x(2)^2;
end
%自定义目标函数2
function y = simple_objective(x)y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
end
运行效果
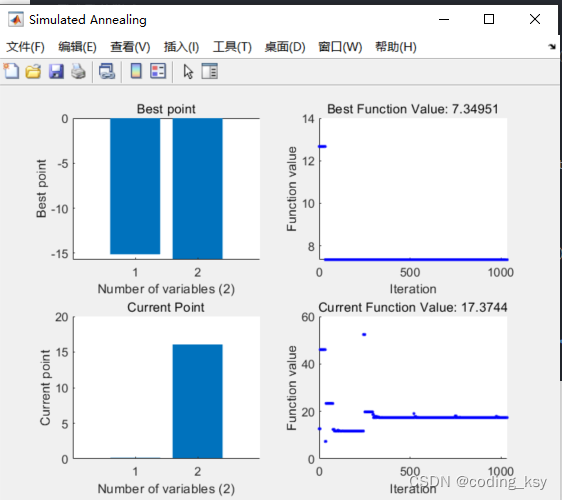
相关文章:

数学建模学习(9):模拟退火算法
模拟退火算法(Simulated Annealing, SA)的思想借 鉴于固体的退火原理,当固体的温度很高的时候,内能比 较大,固体的内部粒子处于快速无序运动,当温度慢慢降 低的过程中,固体的内能减小,粒子的慢慢趋于有序&a…...

带你认识储存以及数据库新技术演进
01经典案例 1.0 潜在问题 02存储&数据库简介 2.1 存储器层级架构 2.1 数据怎么从应用到存储介质 2.1 RAID技术 2.2 数据库 数据库分为 关系型数据库 和 非关系型数据库 2.2.2 非关系型 2.2.1 关系型 2.3 数据库 vs 经典存储-结构化数据管理 2.3.1 数据库 vs 经典存储-事务能…...
腾讯云服务器镜像操作系统大全_Linux_Windows清单
腾讯云CVM服务器的公共镜像是由腾讯云官方提供的镜像,公共镜像包含基础操作系统和腾讯云提供的初始化组件,公共镜像分为Windows和Linux两大类操作系统,如TencentOS Server、Windows Server、OpenCloudOS、CentOS Stream、CentOS、Ubuntu、Deb…...
基于k8s job设计与实现CI/CD系统
方案一:Jenkinsk8sCICD 方案二:kanikok8s jobCICD CICD 基于K8s Job设计流水线 CI方案 工具镜像 云原生镜像打包工具 kaniko的使用 与Jenkins对比 可用性与易用性...
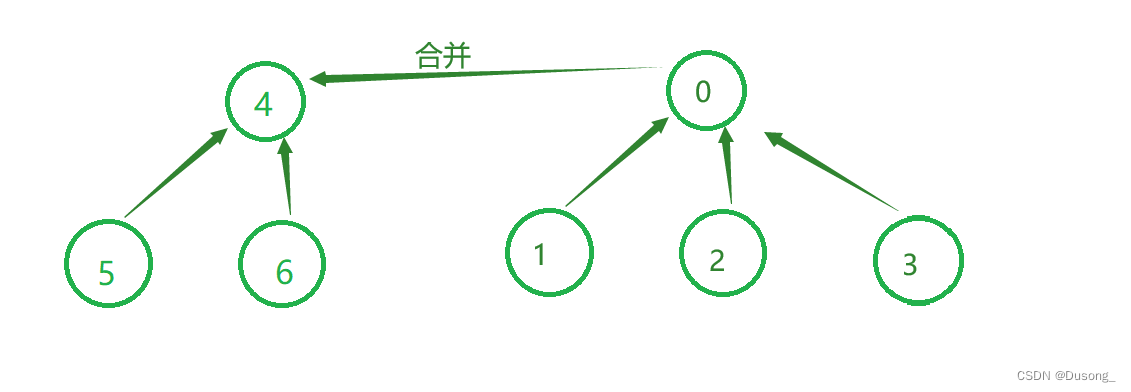
⌈算法进阶⌋图论::并查集——快速理解到熟练运用
目录 一、原理 1. 初始化Init 2. 查询 find 3. 合并 union 二、代码模板 三、练习 1、 990.等式方程的可满足性🟢 2、 1061. 按字典序排列最小的等效字符串🟢 3、721.账户合并 🟡 4、 839.相似字符串组🟡 5、 2812.找出最安全…...

【ROS】fsd_algorithm架构学习与源码分析(致敬)
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍fsd_algorithm架构学习与源码分析。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下&am…...
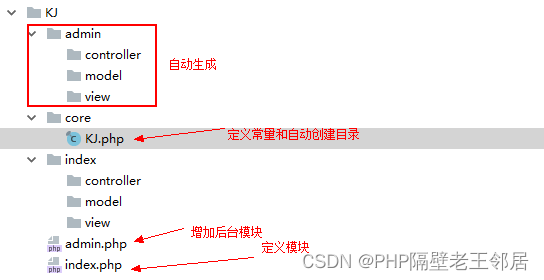
PHP最简单自定义自己的框架定义常量自动生成目录(三)
1、框架入口增加模块定义,实现多模块功能 index.php 定义模块 <?php //定义当前请求模块 define("MODULE",index); require "./core/KJ.php"; 创建后台模块admin.php <?php define("MODULE",admin); require "./cor…...
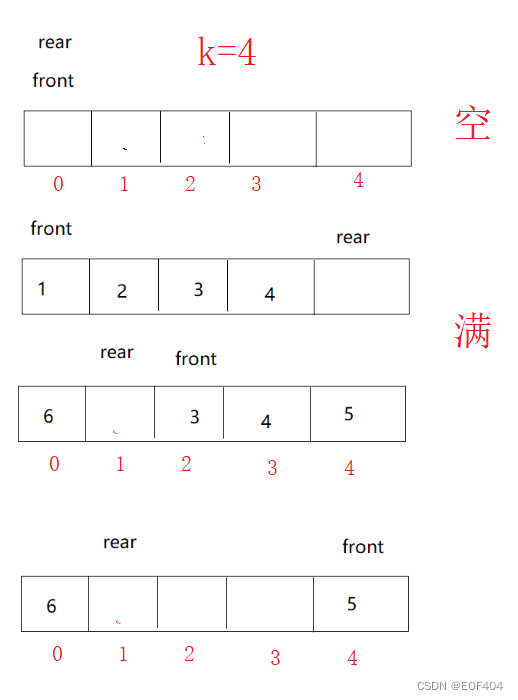
栈和队列详解
目录 栈 栈的概念及结构: 栈的实现: 代码实现: Stack.h stack.c 队列: 概念及结构: 队列的实现: 代码实现: Queue.h Queue.c 拓展: 循环队列(LeetCode题目链接࿰…...
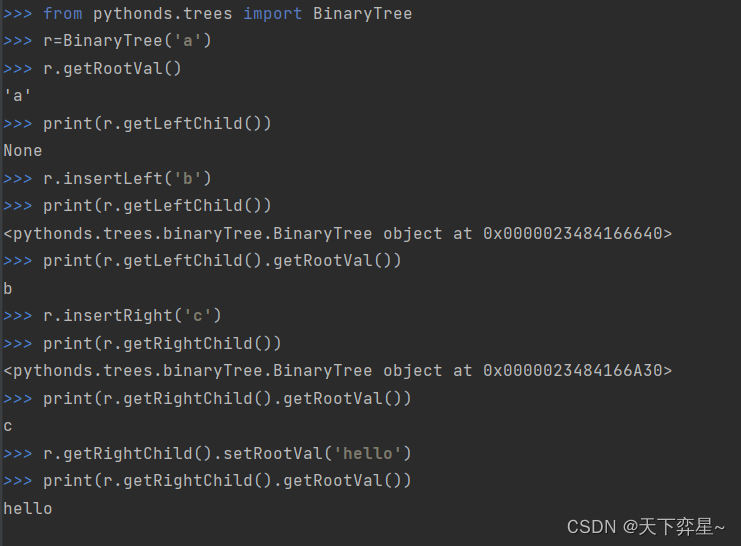
数据结构 | 树的定义及实现
目录 一、树的术语及定义 二、树的实现 2.1 列表之列表 2.2 节点与引用 一、树的术语及定义 节点: 节点是树的基础部分。它可以有自己的名字,我们称作“键”。节点也可以带有附加信息,我们称作“有效载荷”。有效载荷信息对于很多树算法…...
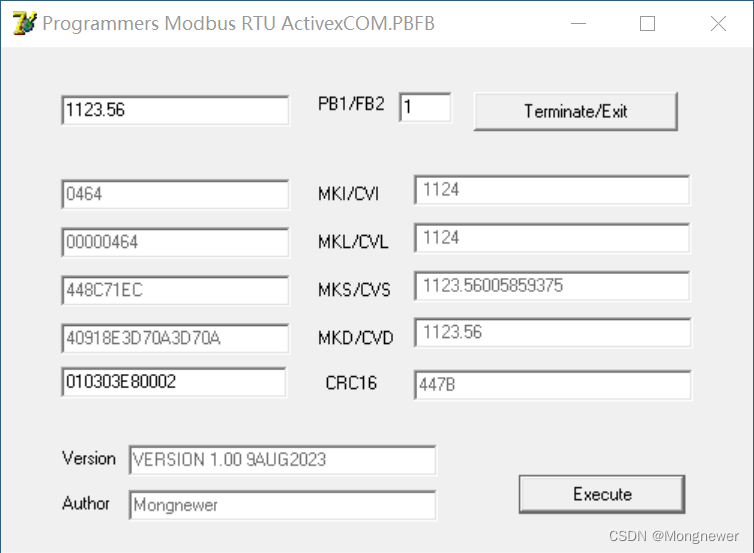
Delphi7通过VB6之COM对象调用FreeBASIC写的DLL功能
VB6写ActiveX COM组件比较方便,不仅PowerBASIC与VB6兼容性好,Delphi7与VB6兼容性也不错,但二者与FreeBASIC兼容性在字符串处理上差距比较大,FreeBASIC是C化的语言,可直接使用C指令。下面还是以实现MKI/CVI, MKL/CVL, M…...
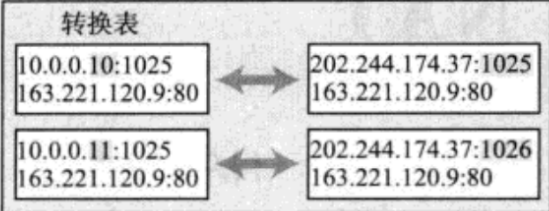
【Linux 网络】NAT技术——缓解IPv4地址不足
NAT技术 NAT 技术背景NAT IP转换过程NAPTNAT 技术的缺陷 NAT(Network Address Translation,网络地址转换)技术,是解决IP地址不足的主要手段,并且能够有效地避免来自网络外部的攻击,隐藏并保护网络内部的计算…...
协议)
Flink 两阶段提交(Two-Phase Commit)协议
Flink 两阶段提交(Two-Phase Commit)是指在 Apache Flink 流处理框架中,为了保证分布式事务的一致性而采用的一种协议。它通常用于在流处理应用中处理跨多个分布式数据源的事务性操作,确保所有参与者(数据源或计算节点…...

【Docker晋升记】No.2 --- Docker工具安装使用、命令行选项及构建、共享和运行容器化应用程序
文章目录 前言🌟一、Docker工具安装🌟二、Docker命令行选项🌏2.1.docker run命令选项:🌏2.2.docker build命令选项:🌏2.3.docker images命令选项:🌏2.4.docker ps命令选项…...

[OnWork.Tools]系列 00-目录
OnWork.Tools系列文章目录 OnWork.Tools系列 01-简介_末叶的博客-CSDN博客OnWork.Tools系列 02-安装_末叶的博客-CSDN博客OnWork.Tools系列 03-软件设置_末叶的博客-CSDN博客OnWork.Tools系列 04-快捷启动_末叶的博客-CSDN博客OnWork.Tools系列 05-系统工具_末叶的博客-CSDN博…...

Cadvisor+InfluxDB+Grafan+Prometheus(详解)
目录 一、CadvisorInfluxDBGrafan案例概述 (一)Cadvisor Cadvisor 产品特点: (二)InfluxDB InfluxDB应用场景: InfluxDB主要功能: InfluxDB主要特点: (三&#…...
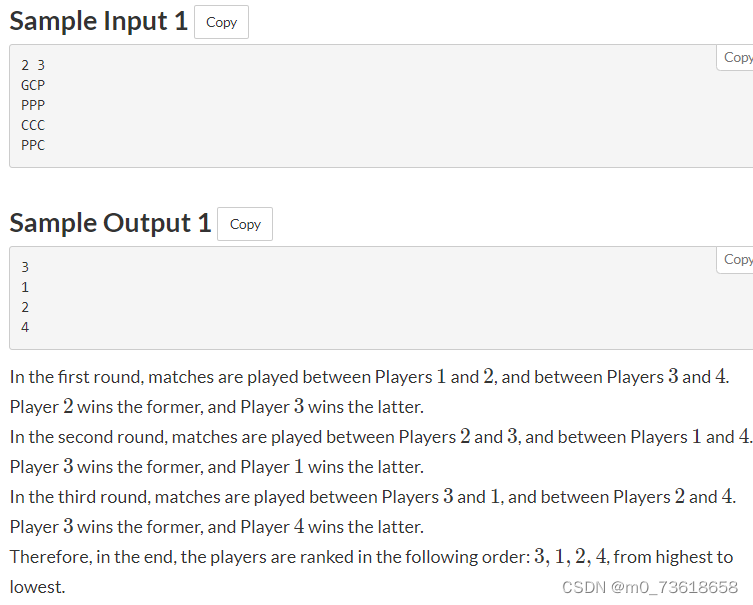
AtcoderABC222场
A - Four DigitsA - Four Digits 题目大意 给定一个整数N,其范围在0到9999之间(包含边界)。在将N转换为四位数的字符串后,输出它。如果N的位数不足四位,则在前面添加必要数量的零。 思路分析 可以使用输出流的格式设…...
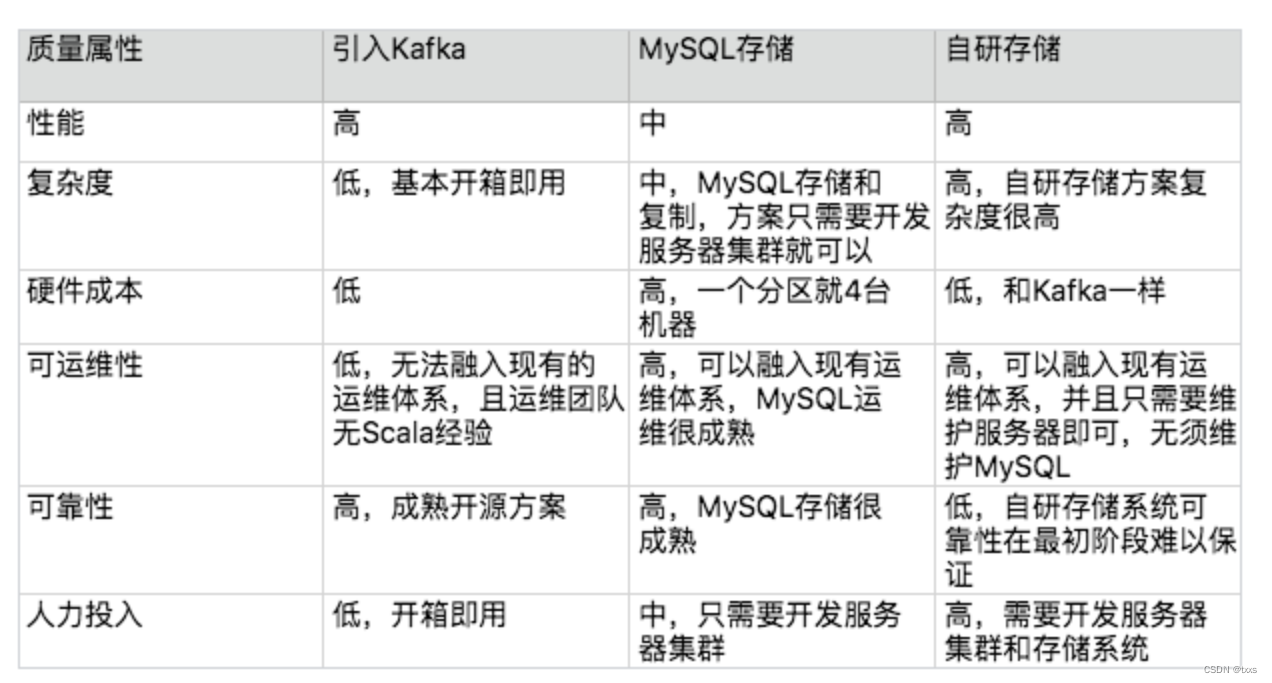
架构实践方法
一、识别复杂度 将主要的复杂度问题列出来,然后根据业务、技术、团队等综合情况进行排序,优先解决当前面临的最主要的复杂度问题。对于按照复杂度优先级解决的方式,存在一个普遍的担忧:如果按照优先级来解决复杂度,可…...
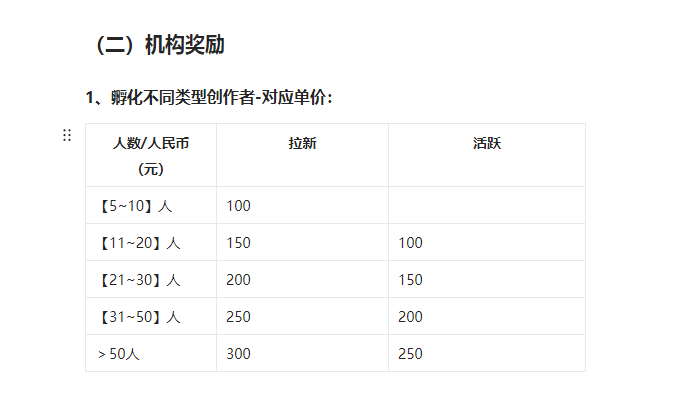
点淘的MCN机构申请详细入驻指南!
消费趋势的变化,来自消费人群的变化。 后疫情时代,经济复苏的反弹力度不足,人们开始怀疑我们正从前几年的消费升级,跌入消费降级的时代,但这并不能准确概括消费市场的变化。 仔细翻看各大奢侈品集团的财报࿰…...
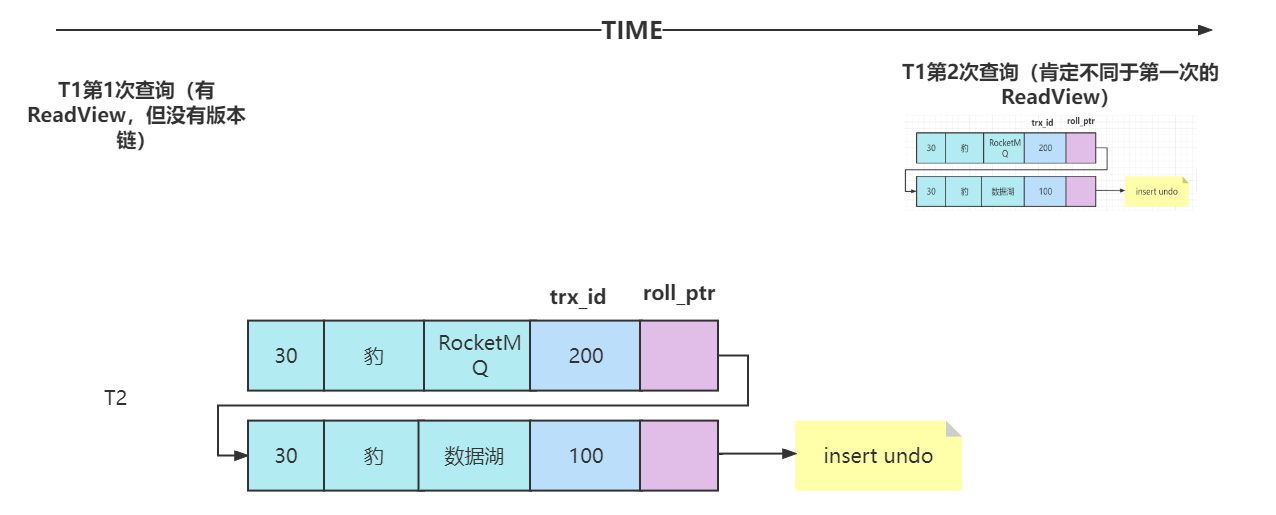
事务和事务的隔离级别
1.4.事务和事务的隔离级别 1.4.1.为什么需要事务 事务是数据库管理系统(DBMS)执行过程中的一个逻辑单位(不可再进行分割),由一个有限的数据库操作序列构成(多个DML语句,select语句不包含事务&…...
)
每日一题 34在排序数组中查找元素的第一个和最后一个位置(二分查找)
题目 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。 示例 1&…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
