Scratch 详解 之 线性→代数之——求两线段交点坐标

可能有人要问:求交点坐标有什么用呢?而且为啥要用线代来求?直线方程不行吗???
这个问题,我只能说,直线方程计算的次数过多了,而且动不动就要考虑线的方向,90°的直线的斜率不存在,所以用向量(也就是线性代数)来算更好点。至于有什么用处,也许一些算法需要吧,比如计算一线是否与矩形相交来进行判定。
本教程涉及线代的内容较少,除了思想,你还会学到:
如何判断两线段是否相交?相似三角形的性质。一点到另一点的方向。三角函数相关知识。
还有,向量叉乘的正负特性,向量叉乘的计算,单位向量的计算,一点至另一点的向量表示方法,向量的数量积(点积)的几何意义与计算。
线性代数的运用举例:
- 求交点(本教程)
- 将凹多边形分为三角形(用于渲染)
- 距离一条直线最短的点(叉乘)
- 各种方向判断问题。
Part 1:怎样判断线段是否相交?
此部分需要先理解向量叉乘的意义,我先通俗地讲一下
首先,看下图。
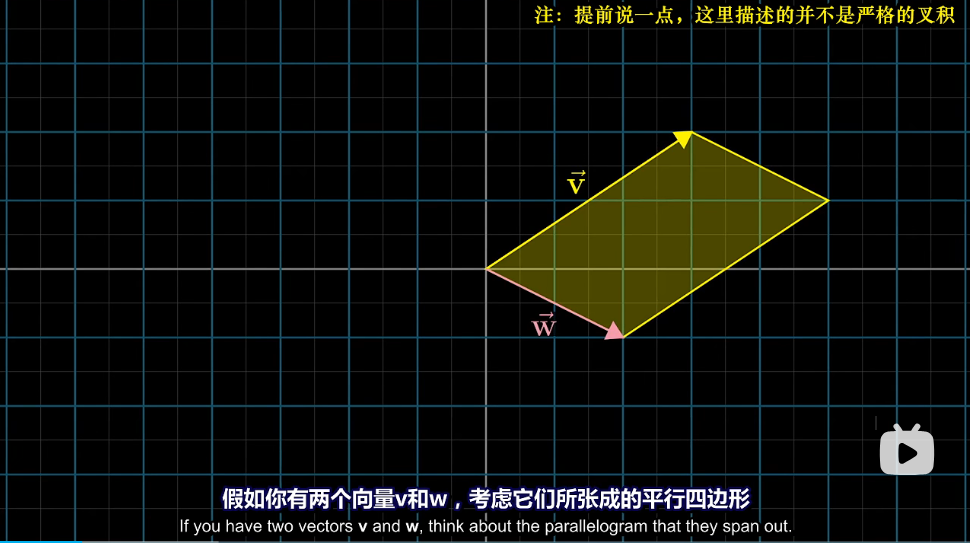
我们有两个向量v与向量w,那么v(向量两字省略,后面也是如此)与w所形成的平行四边形的面积,就是v×w的结果(×即为叉乘),但是叉乘具有正负性,
如果v在w的左边,那么v×w<0(也就是负的),
如果v在w的右边,那么v×w>0(也就是正的),
当v与w重合或相反,很容易想到结果是0(没有张成平行四边形),
总结一下,顺时针负,逆时针正。
对了,对于一个向量[x1,y1]与向量[x2,y2],他们的叉乘就是这两个向量的行列式(这句可以看不懂),也就是x1*y2-x2*y1。
根据以上结论,我们就可以开始研究两条线怎样才会相交。

相交示意图
如图,线段AB与线段CD相交,连接AB的端点到CD形成向量a,b,c,d。
我们发现,a叉乘b的结果与d叉乘c异号。
再来看不相交的。

不相交示意图
向量a叉乘b与d叉乘c的的符号一样
接下来看看特殊的。
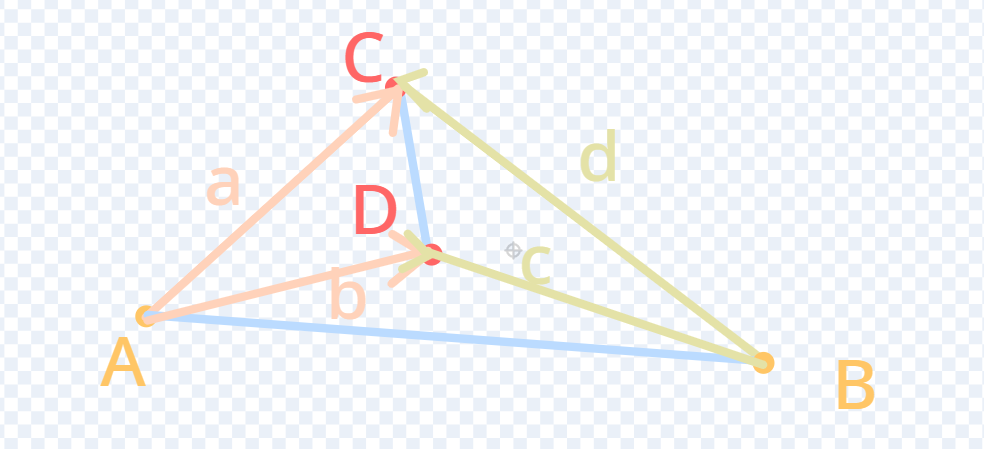
特殊的不相交
这次a叉乘b与d叉乘c的符号不同,这种错误要把d与b互换就行了,如下图:
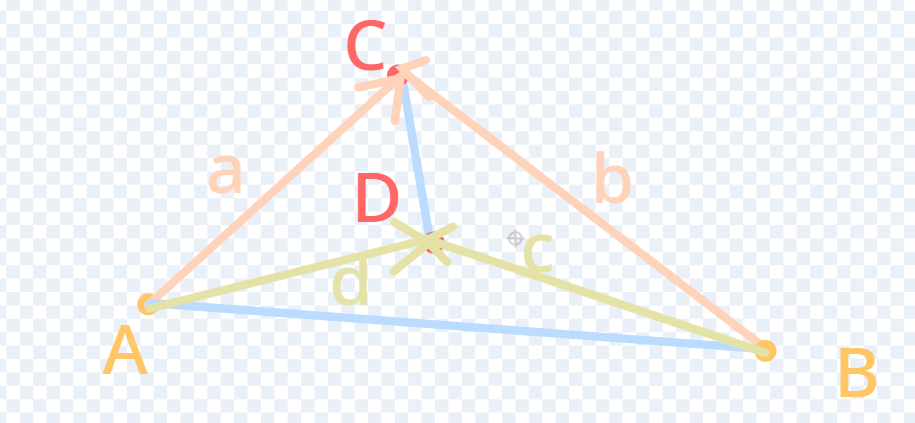
更正后的(注意向量叉乘时要让端点在同一个地方。
这回,a叉乘b与d叉乘c的符号又相同了!
总结一下,若a(x1,y1),b(x2,y2),c(x3,y3),d(x4,y4),(都是向量)那么上面的一大堆用数学来表示就是下面这个图:
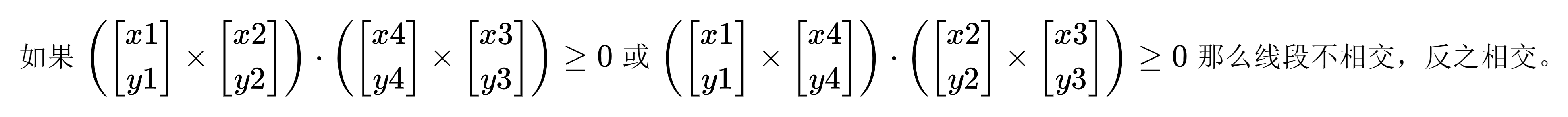
上图中,×代表叉乘,·代表乘法,相乘大于等于就是同号的意思啦。
或者把“或”改为“与”,然后把≥改为<,那么线段就相交,反之不相交。
接下来开始用代码实现!
这里呢,我先简简单单地做了一个绘制系统:

然后,创建一个自制积木
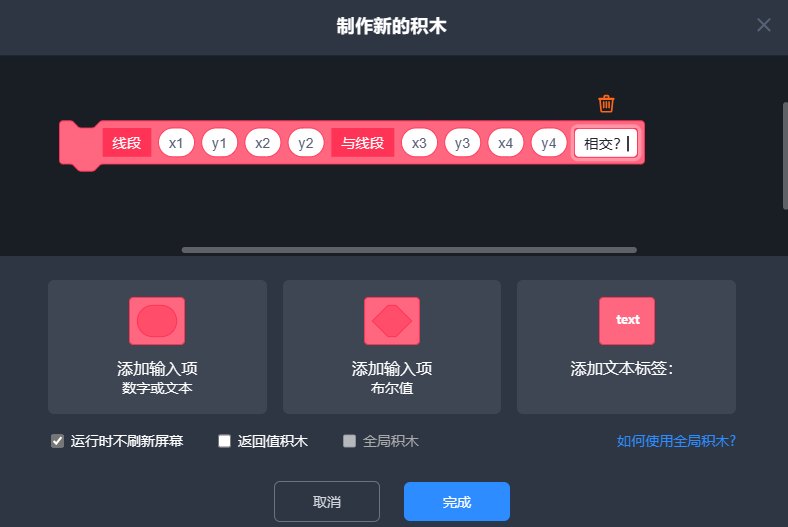
那么,我们就可以写下这样的代码,来实现判断两线段是否相交:先计算a,b,c,d的向量,然后根据叉乘公式(别忘了,就是行列式:x1*y2-x2*y1),进行判断。
那向量怎么求呢?
这个问题有个公式,对于在平面直角坐标系内的点A(x1,y1)与点B(x2,y2),向量AB即为[(x2-x1),(y2-y1)]
我们直接上代码。
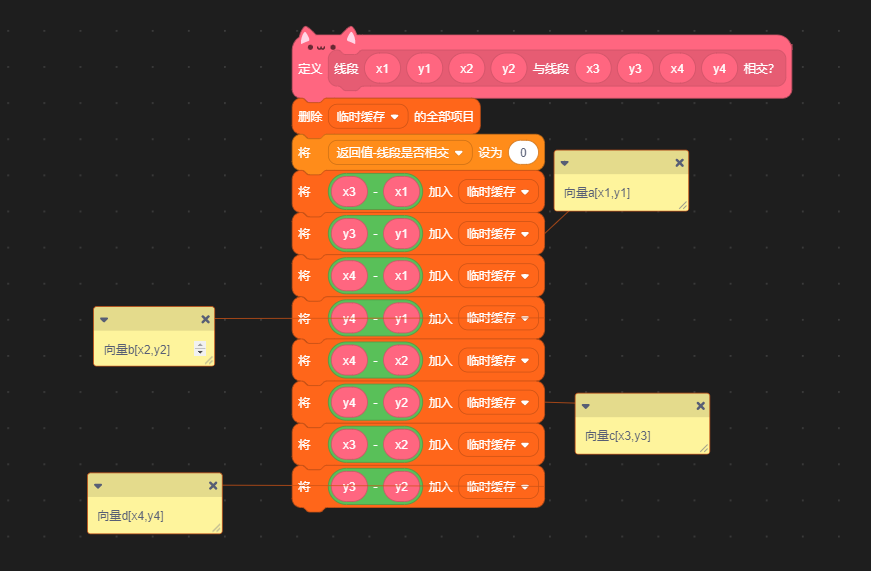
计算向量
首先是计算向量,然后保存在缓存里面,并且初始化返回值。接下来我们要进行叉乘,并且判断是否<0,如下图:

叉乘并判断
这样,一个香蕉 相交判断就做完力,可要是判断线段是否在线上,那该怎么弄呢?
我们知道,如果一个向量与另一个向量的夹角为0°或者180°,那么他们的叉乘为0。在线上时,两个向量分别指向另外两个端点,就形成了180度;
如果这个点在另条线段的延长线上,那么这两个向量的夹角是0°;
那如果点在端点上呢?
想想看,那么一个向量的模长(长度)就是0了,好像怎么叉乘还是0。
那么这3种可能都会出现叉乘为0,我们就可以加上等于0的判断,返回相应的值。,如下图:

Part 2:计算交点
部分1总算是写完了,接下来便是交点坐标的计算。
1.理清思路。

线段AB与CD交于点E
如图,点H为C投影至AB的点,G同理。(投影就是向它做垂线),投影长度分别为d1,d2。
我们要求的是点E的坐标,为此,我先讲一下:什么是相似三角形?(六年级即可懂,初三及以上学生请跳过)

两个三角形
如图,AB平行于CF平行于DE,由于平行线,我们知道图中有大多相同的角,都已经标在图中。
我们观察一下,这两个三角形三个角(或者两个)是一样的(真的),但是他们并不全等,像这样三个角都相等的两个三角形,我们称它们相似(不知道准不准确啊,我才初一()
对于两个相似三角形,它们的对应边长的比值都是相等的。比如:
AB/BC=DE/DC , AB/DE=AC/CE。
不知道你有没有看懂,反正就这些了。
再来看刚刚的图:
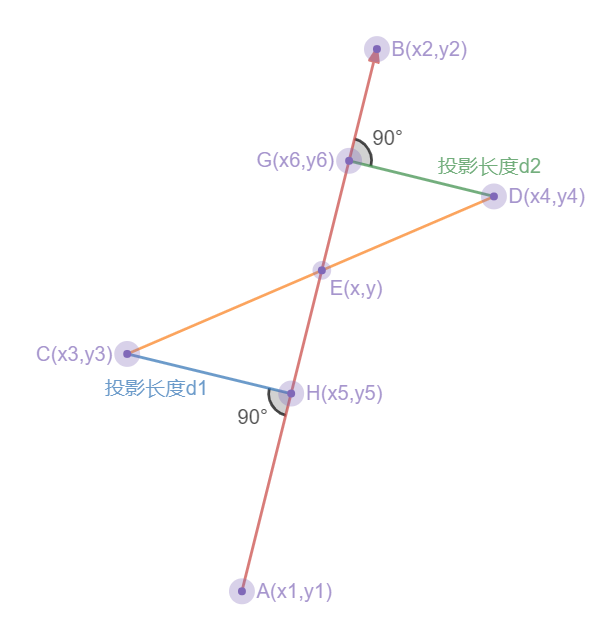
求交点E的坐标
首先,我们看三角形DGE与三角形CHE,由于俩对顶角相等(∠CEH与∠GED),而且由于是投影,所以有个角都是90度,所以,这两个三角形相似。
相似?那就是比值相等呗!那不就是交点(x, y)距离两点的比例则和d1, d2的比例相同吗?(d1/d2=EH/GE)
我们看看,EH占GH的几分之几呢?是EH/GH吧,现在,由于比例相同,我们可以把EH/GH写成d1/(d1+d2)的形式{也就是EH/GH=EH/(EH+GE)=d1/(d1+d2)}。
同理,GE/GH也能写成d2/(d1+d2)的形式{也就是GE/GH=GE/(EH+GE)=d2/(d1+d2)}。
哎,权重(占比)知道了,坐标不就好办了嘛!(x,y)就是 H坐标*占比+G坐标*占比啊,即

注意权重不要写反了
2.计算投影。
你肯定要问我:d1,d2咋算啊???还有,你投影坐标是个啥???
这就要说一下向量点积(·)的几何意义了。

向量点积示意图
向量点积的几何意义是,一个向量向另一向量投影,然后再乘上另一向量的长度(模长)之后的点与端点的距离。在图中,向量AB·向量AD得到AE的长度,即AC*AD。
坐向量点积公式1(坐标系):a·b=(x1,y1)·(x2,y2)=x1*x2+y1*y2。其中,a和b分别为两个向量,(x1,y1)和(x2,y2)
向量点积公式2(几何):a·b=|a|*|b|*cosθ,θ是a,b的夹角
向量叉乘公式(几何):a·b=|a|*|b|*sinθ,θ是a,b的夹角
哎,我们发现有个投影!那如果上面公式中b的模长(长度)为1呢?
由于点积的几何意义,当b的模长为1时,a·b就是a向b的投影!
那我们就可以计算投影了。

“投影”
给定一个直线外点(x0, y0)和直线上两点(x1, y1), (x2, y2),计算投影点(x, y)。
如何把向量AB投影至向量AC?
首先,求出AC的单位向量(模长为1,紫色),然后向量AB·紫色向量,就得到了AD的长度,最后,求出AC的方向,在AC方向上移动AD长度,就是点D的坐标啦。(耶)
至于AC方向怎么求,可以用反三角函数——arctan来求,这里不多说,直接上代码。

接下来,怎么求出单位向量?
对于一个向量[x,y]它的单位向量是[x/√(x^2+y^2),y/√(x^2+y^2)],其实就是向量除以模长。如下图:

单位向量公式
那么就剩点积了。

点积
接下来我们就可以计算投影了。

一半的投影(由于可能要用缓存,所以使用的是倒数第1和2项)
啊,我们求出AD长度和方向,但怎么知道他的横纵坐标呢?

求A'B与BD
这是刚刚那幅图的一部分,我们要求的是AB的x长度和y长度(横纵坐标差),也就是A'B与BD
因为∠AA'B=90°,所以三角形AA'B为直角三角形
对于直角三角形,我们有一个定理:每个角度的三角形三个边都有一个固定的比值。
也就是说,在三角形AA'B中,A'B/AB与AA'(长度也就是BD)/AB的值是固定的。
在这里,我们把AA'叫做角a的邻边,A'B叫做角a的对边,AB叫做角a的斜边。(可以不记住)
我们把对边与斜边的比叫做正弦,记作sin,即sin a=对/斜;
邻边与斜边的比值叫做余弦,记作cos,即cos a=邻/斜;
还有正切(tan)和反三角等函数,感兴趣的可以自己搜,我们这次只用sin和cos。
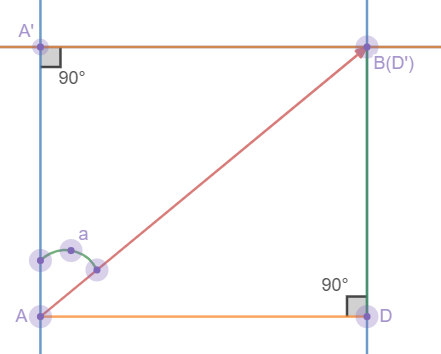
我们知道AB与角a的值了,那A'B和A'A就很好求了,
sin a=A'B/AB,AB*sin a=A'B/AB*AB=A'B(求出来了!)
cos a=A'A/AB,AB*cos a=A'A/AB*AB=A'A
那么横纵坐标差也就求出来了,代码如下所示:

投影
不要忘记还要算出投影距离(勾股定理)

最终代码如图所示

更改绘制代码
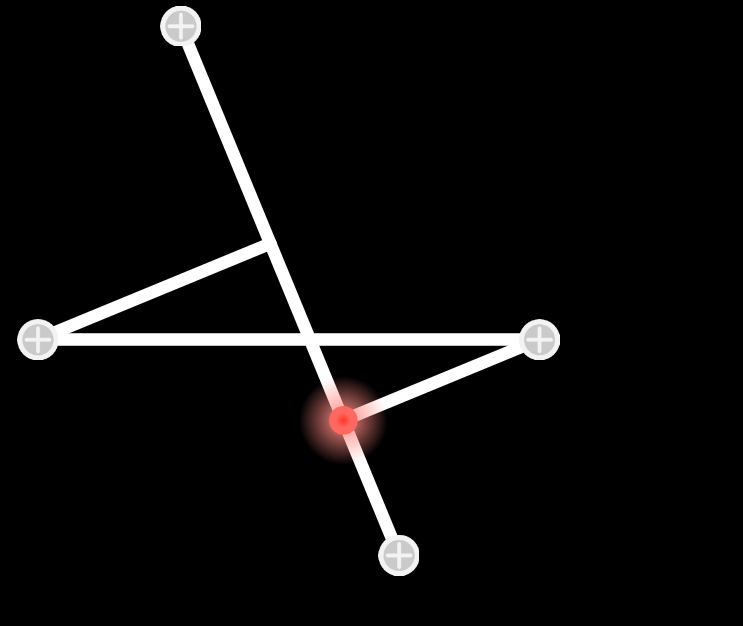
图像
我们发现投影是个垂线,说明程序正常。(在做程序时要养成检测的习惯!)wonderful!
3.计算交点坐标

刚刚推出的公式
这是我们刚刚推出的交点坐标公式,在这里,d1,d2和x6,y6,x5,y5我们都可以算出来,那么x,y也就出来了!
首先,我们要先把一个线段投影到另一个线段上

线段交点坐标的一部分
然后,算出每个点的权重(就是d1 d2那个):

线段交点坐标的一部分*2
最后,将权重与点坐标相乘并相加,即为相交点坐标。
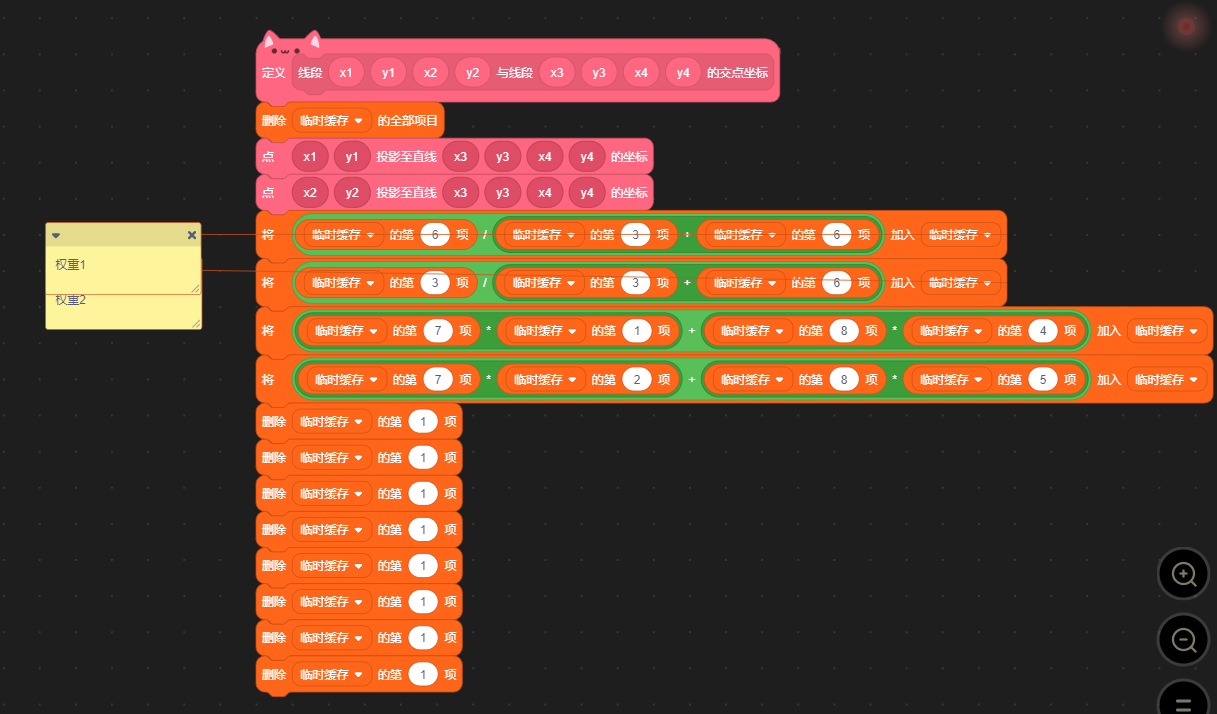
线段交点坐标(全)
Part 3:结尾
到此,两个线段的交点坐标已经做完了,以下是全部代码:

所有代码
在绘制与移动区域内,我添加了透明度变化,防止混淆。
我们来测试一下。

效果展示
资源下载链接
不想写代码的,可以下载这个配套资源:Scratch 教程作品:线段交点坐标
感谢支持
相关文章:

Scratch 详解 之 线性→代数之——求两线段交点坐标
可能有人要问:求交点坐标有什么用呢?而且为啥要用线代来求?直线方程不行吗??? 这个问题,我只能说,直线方程计算的次数过多了,而且动不动就要考虑线的方向,90的…...

Python-组合数据类型
今天要介绍的是Python的组合数据类型 整理不易,希望得到大家的支持,欢迎各位读者评论点赞收藏 感谢! 目录 知识点知识导图1、组合数据类型的基本概念1.1 组合数据类型1.2 集合类型概述1.3 序列类型概述1.4 映射类型概述 2、列表类型2.1 列表的…...

vue3+vue-simple-uploader实现大文件上传
vue-simple-uploader本身是基于vue2实现,如果要使用vue3会报错。如何在vue3中使用,可参考我的另一篇文章:解决vue3中不能使用vue-simple-uploader__Jyann_的博客-CSDN博客 一.实现思路 使用vue-simple-uploader组件的uploader组件,设置自动上传为false,即可开启手动上传。…...
自适应变异麻雀搜索算法及其Matlab实现
麻雀搜索算法( sparrow search algorithm,SSA) 是2020 年新提出的一种元启发式算法[1],它是受麻雀种群的觅食和反捕食行为启发,将搜索群体分为发现者、加入者和侦察者 3 部分,其相互分工寻找最优值,通过 19 个标准测试…...
ETL技术入门之ETLCloud初认识
首先ETL是什么? ETL代表“Extract, Transform, Load”,是一种用于数据集成和转换的过程。它在数据管理和分析中扮演着重要的角色。下面我们将分解每个步骤: Extract(抽取): 这一步骤涉及从多个不同的数据源…...

uniapp项目如何运行在微信小程序模拟器上
在HbuilderX中的小程序写完后自己一定要保存,否则会出不来效果 那么怎么让uniapp项目运行在微信小程序开发工具中呢 1 在hbuilderx中点击运行到小程序模拟器 2 然后在项目目录中会生成一个文件夹 在微信小程序开发软件中的工具>安全设置>打开端口 或者在微…...
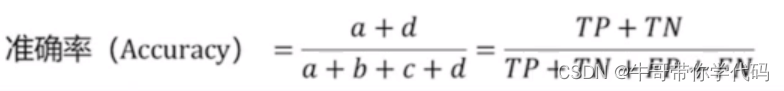
数据挖掘全流程解析
数据挖掘全流程解析 数据指标选择 在这一阶段,使用直方图和柱状图的方式对数据进行分析,观察什么数据属性对于因变量会产生更加明显的结果。 如何绘制直方图和条形统计图 数据清洗 观察数据是否存在数据缺失或者离群点的情况。 数据异常的两种情况…...

详细介绍如何对音乐信息进行检索和音频节拍跟踪
在本文中,我们将了解节拍的概念,以及我们在尝试跟踪节拍时面临的挑战。然后我们将介绍解决问题的方法以及业界最先进的解决方案。 介绍 音乐就在我们身边。每当我们听到任何与我们的心灵和思想相关的音乐时,我们就会迷失其中。我们下意识地随着听到的节拍而敲击。您一定已…...
Java课题笔记~ HTTP协议(请求和响应)
Servlet最主要的作用就是处理客户端请求,并向客户端做出响应。为此,针对Servlet的每次请求,Web服务器在调用service()方法之前,都会创建两个对象 分别是HttpServletRequest和HttpServletResponse。 其中HttpServletRequest用于封…...

在x86下运行的Ubuntu系统上部署QEMU用于模拟RISC-V硬件环境
1.配置工作环境 sudo apt install gcc bison flex libncurses-dev ninja-build \pkg-config build-essential zlib1g-dev pkg-config libglib2.0-dev \binutils-dev libboost-all-dev autoconf libtool libssl-dev \libpixman-1-dev python-capstone virtualenv software-prop…...

网络爬虫选择代理IP的标准
Hey,小伙伴们!作为一家http代理产品供应商,我知道网络爬虫在选择代理IP时可能会遇到些问题,毕竟市面上有很多选择。别担心!今天我要给大家分享一些实用的建议,帮助你们选择适合网络爬虫的代理IP。一起来看看…...

RxJava 复刻简版之三,map 多次中转数据
案例代码:https://gitee.com/bobidali/lite-rx-java/commit/292e9227a5491f7ec6a07f395292ef8e6ff69290 RxJava 的调用第一步是封装了观察者接受了数据的处理,进一步就是使用 map 将数据操作传递给上下游 1、类似Observer.create 创建一个简单的观察者…...
)
06 Word2Vec模型(第一个专门做词向量的模型,CBOW和Skip-gram)
博客配套视频链接: https://space.bilibili.com/383551518?spm_id_from=333.1007.0.0 b 站直接看 配套 github 链接:https://github.com/nickchen121/Pre-training-language-model 配套博客链接:https://www.cnblogs.com/nickchen121/p/15105048.html 神经网络语言模型(NNL…...
Axure RP9小白安装教程
第一步: 打开:Axure中文学习网 第二步: 鼠标移动软件下载,点击Axure RP 9下载既可 第三步: 注意:Axure RP 9 MAC正式版为苹果版本,Axure RP 9 WIN正式版为Windows版本 中文汉化包ÿ…...

腾讯云CVM服务器2核2g1m带宽支持多少人访问?
腾讯云2核2g1m的服务器支持多少人同时访问?2核2g1m云服务器短板是在1M公网带宽上,腾讯云服务器网以网站应用为例,当大规模用户同时访问网站时,很大概率会卡在公网带宽上,所以压根就谈不上2核2G的CPU内存计算性能是否够…...

8.12学习笔记
在PyTorch中,Dataset和DataLoader是用于处理数据的两个重要类。Dataset类是一个抽象类,用于表示数据集。它的主要作用是将数据加载到内存中,并提供一种统一的方式来访问数据。为了使用Dataset类,你需要继承它并实现两个方法&#…...

计算机体系中的不同的缓存存储层级说明
分级说明 L1缓存的标准延迟是4个周期。这意味着,当CPU请求数据时,L1缓存需要4个时钟周期来将数据传输给CPU。 L2缓存的标准延迟是12个周期。相对于L1缓存,L2缓存的容量更大,但其读取速度更慢,需要更多的时钟周期来传输…...
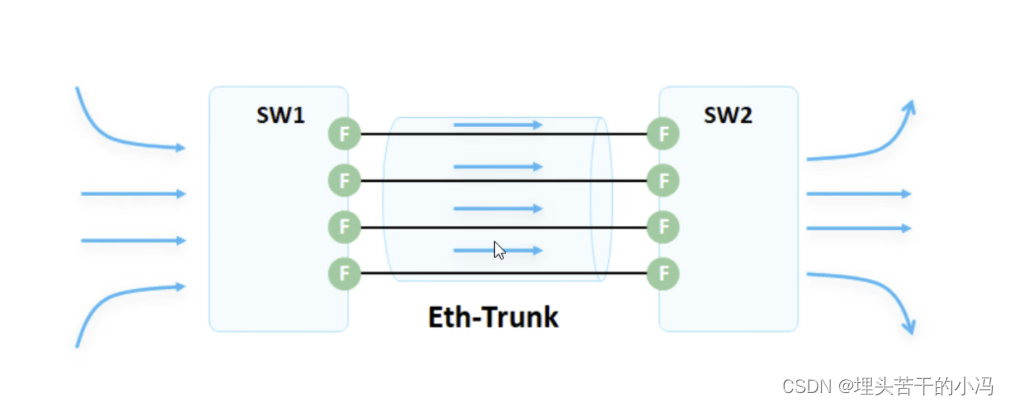
HCIP 链路聚合技术
1、链路聚合概述 为了保证网络的稳定性,仅仅是设备进行备份还不够,我们需要针对我们的链路进行备份,同时也增加了链路的利用率,提高带宽。避免一条链路出现故障,导致网络无法正常通信。这就可以使用链路聚合技术。 以…...

网页爬虫中常用代理IP主要有哪几种?
各位爬虫探索者,你是否有想过在网页爬虫中使用代理IP来规避限制实现数据自由?在这篇文章中,作为一名IP代理产品供应商,我将为你揭示常见的网页爬虫代理IP类型,让你在爬虫的世界中游刃有余! 一、免费公开代理…...
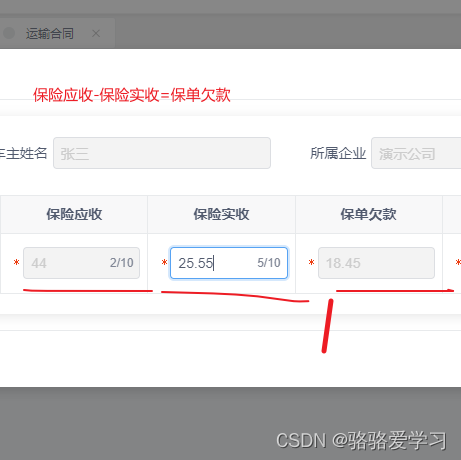
Js小数运算精度缺失的解决方法
项目场景: 提示:项目需求截图: 问题描述 众所周知Js做运算时0.10.2不等于0.3,目前项目需要计算关于金额的选项,涉及到金额保留后两位。保单欠款是根据用户输入的保单应收和保单欠款自动计算的。 原因分析: 产生浮点数…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
