786. 第k个数
文章目录
- Question
- Ideas
- Code
Question
给定一个长度为 n
的整数数列,以及一个整数 k
,请用快速选择算法求出数列从小到大排序后的第 k
个数。
输入格式
第一行包含两个整数 n
和 k
。
第二行包含 n
个整数(所有整数均在 1∼109
范围内),表示整数数列。
输出格式
输出一个整数,表示数列的第 k
小数。
数据范围
1≤n≤100000
,
1≤k≤n
输入样例:
5 3
2 4 1 5 3
输出样例:
3
Ideas
Code
// 快排步骤(O(nlgn)):
// 1.寻找分界点x,a[l + r >> 1]
// 2.划分区间,使得左边均<=x,右边均>=x
// 3.递归左右两边
// 快速搜索步骤(O(n))
// 当进行到第2步时,左区间严格<=右区间,所以第k小的数要么在左区间,要么在右区间,
// 只需要递归一边即可,这由k与左区间的元素个数有关#include <iostream>using namespace std;const int N = 1E5 + 10;
int a[N];int quick_choose(int *a, const int& l, const int& r, const int& k)
{if (l >= r) return a[l];int x = a[l + r >> 1];int i = l - 1, j = r + 1;while(i < j){do i ++; while(a[i] < x); // 快排左边寻找a[i] >= xdo j --; while(a[j] > x);if (i < j) swap(a[i], a[j]);}int sl = j - l + 1;if (k <= sl) return quick_choose(a, l, j, k); // 左边区间的数目else return quick_choose(a,j + 1, r, k - sl);
}
int main()
{int n, k;scanf("%d%d", &n, &k);for (int i = 0; i < n; i ++) scanf("%d", &a[i]);cout << quick_choose(a, 0, n - 1, k) << endl;return 0;
}
相关文章:

786. 第k个数
文章目录 QuestionIdeasCode Question 给定一个长度为 n 的整数数列,以及一个整数 k ,请用快速选择算法求出数列从小到大排序后的第 k 个数。 输入格式 第一行包含两个整数 n 和 k 。 第二行包含 n 个整数(所有整数均在 1∼109 范围内&…...

用友-NC-Cloud远程代码执行漏洞[2023-HW]
用友-NC-Cloud远程代码执行漏洞[2023-HW] 一、漏洞介绍二、资产搜索三、漏洞复现PoC小龙POC检测脚本: 四、修复建议 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失&#…...
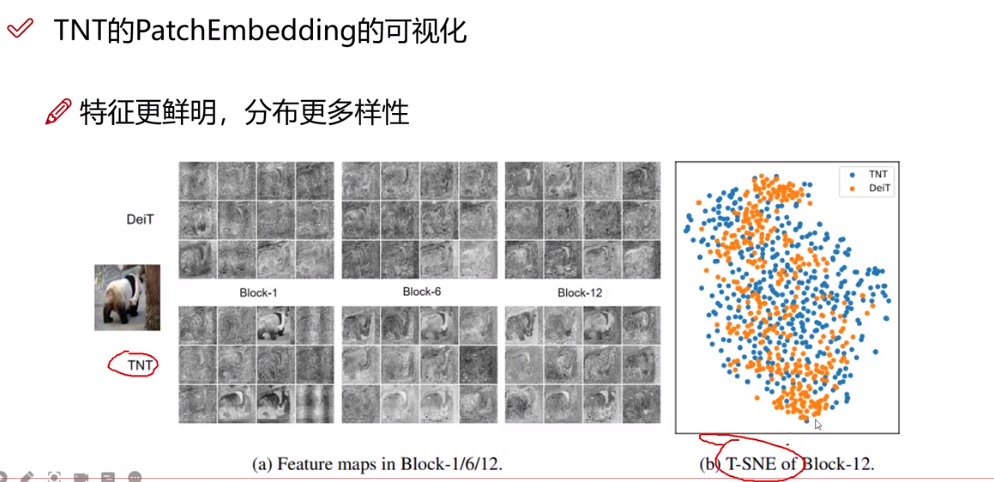
Transformer(二)(VIT,TNT)(基于视觉CV)
目录 1.视觉中的Attention 2.VIT框架(图像分类,不需要decoder) 2.1整体框架 2.2.CNN和Transformer遇到的问题 2.3.1CNN 2.3.2Transformer 2.3.3二者对比 2.4.公式理解 3TNT 参考文献 1.视觉中的Attention 对于人类而言看到一幅图可以立…...

Scratch 详解 之 线性→代数之——求两线段交点坐标
可能有人要问:求交点坐标有什么用呢?而且为啥要用线代来求?直线方程不行吗??? 这个问题,我只能说,直线方程计算的次数过多了,而且动不动就要考虑线的方向,90的…...

Python-组合数据类型
今天要介绍的是Python的组合数据类型 整理不易,希望得到大家的支持,欢迎各位读者评论点赞收藏 感谢! 目录 知识点知识导图1、组合数据类型的基本概念1.1 组合数据类型1.2 集合类型概述1.3 序列类型概述1.4 映射类型概述 2、列表类型2.1 列表的…...

vue3+vue-simple-uploader实现大文件上传
vue-simple-uploader本身是基于vue2实现,如果要使用vue3会报错。如何在vue3中使用,可参考我的另一篇文章:解决vue3中不能使用vue-simple-uploader__Jyann_的博客-CSDN博客 一.实现思路 使用vue-simple-uploader组件的uploader组件,设置自动上传为false,即可开启手动上传。…...
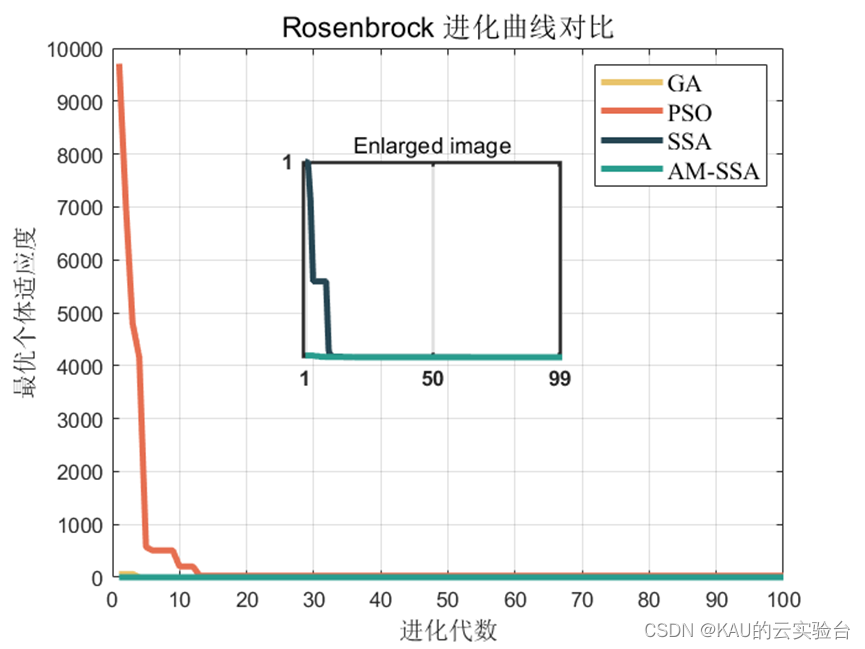
自适应变异麻雀搜索算法及其Matlab实现
麻雀搜索算法( sparrow search algorithm,SSA) 是2020 年新提出的一种元启发式算法[1],它是受麻雀种群的觅食和反捕食行为启发,将搜索群体分为发现者、加入者和侦察者 3 部分,其相互分工寻找最优值,通过 19 个标准测试…...
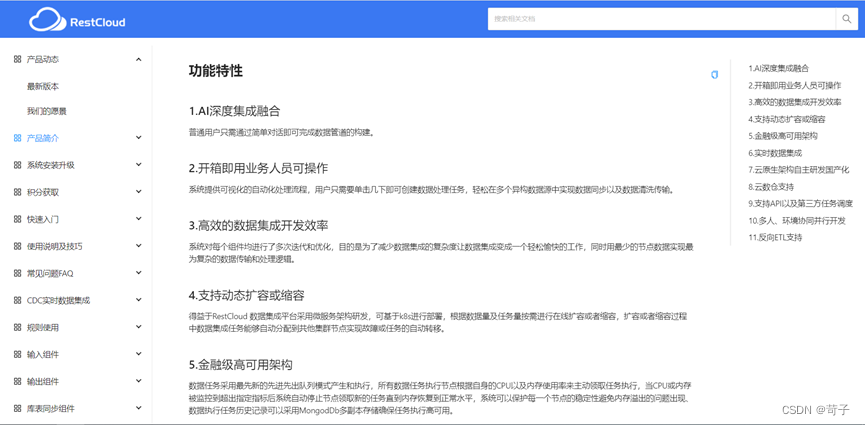
ETL技术入门之ETLCloud初认识
首先ETL是什么? ETL代表“Extract, Transform, Load”,是一种用于数据集成和转换的过程。它在数据管理和分析中扮演着重要的角色。下面我们将分解每个步骤: Extract(抽取): 这一步骤涉及从多个不同的数据源…...

uniapp项目如何运行在微信小程序模拟器上
在HbuilderX中的小程序写完后自己一定要保存,否则会出不来效果 那么怎么让uniapp项目运行在微信小程序开发工具中呢 1 在hbuilderx中点击运行到小程序模拟器 2 然后在项目目录中会生成一个文件夹 在微信小程序开发软件中的工具>安全设置>打开端口 或者在微…...
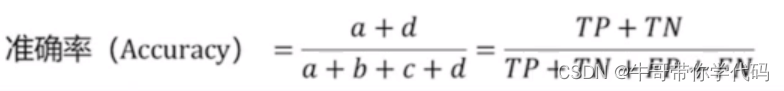
数据挖掘全流程解析
数据挖掘全流程解析 数据指标选择 在这一阶段,使用直方图和柱状图的方式对数据进行分析,观察什么数据属性对于因变量会产生更加明显的结果。 如何绘制直方图和条形统计图 数据清洗 观察数据是否存在数据缺失或者离群点的情况。 数据异常的两种情况…...

详细介绍如何对音乐信息进行检索和音频节拍跟踪
在本文中,我们将了解节拍的概念,以及我们在尝试跟踪节拍时面临的挑战。然后我们将介绍解决问题的方法以及业界最先进的解决方案。 介绍 音乐就在我们身边。每当我们听到任何与我们的心灵和思想相关的音乐时,我们就会迷失其中。我们下意识地随着听到的节拍而敲击。您一定已…...
Java课题笔记~ HTTP协议(请求和响应)
Servlet最主要的作用就是处理客户端请求,并向客户端做出响应。为此,针对Servlet的每次请求,Web服务器在调用service()方法之前,都会创建两个对象 分别是HttpServletRequest和HttpServletResponse。 其中HttpServletRequest用于封…...

在x86下运行的Ubuntu系统上部署QEMU用于模拟RISC-V硬件环境
1.配置工作环境 sudo apt install gcc bison flex libncurses-dev ninja-build \pkg-config build-essential zlib1g-dev pkg-config libglib2.0-dev \binutils-dev libboost-all-dev autoconf libtool libssl-dev \libpixman-1-dev python-capstone virtualenv software-prop…...

网络爬虫选择代理IP的标准
Hey,小伙伴们!作为一家http代理产品供应商,我知道网络爬虫在选择代理IP时可能会遇到些问题,毕竟市面上有很多选择。别担心!今天我要给大家分享一些实用的建议,帮助你们选择适合网络爬虫的代理IP。一起来看看…...

RxJava 复刻简版之三,map 多次中转数据
案例代码:https://gitee.com/bobidali/lite-rx-java/commit/292e9227a5491f7ec6a07f395292ef8e6ff69290 RxJava 的调用第一步是封装了观察者接受了数据的处理,进一步就是使用 map 将数据操作传递给上下游 1、类似Observer.create 创建一个简单的观察者…...
)
06 Word2Vec模型(第一个专门做词向量的模型,CBOW和Skip-gram)
博客配套视频链接: https://space.bilibili.com/383551518?spm_id_from=333.1007.0.0 b 站直接看 配套 github 链接:https://github.com/nickchen121/Pre-training-language-model 配套博客链接:https://www.cnblogs.com/nickchen121/p/15105048.html 神经网络语言模型(NNL…...
Axure RP9小白安装教程
第一步: 打开:Axure中文学习网 第二步: 鼠标移动软件下载,点击Axure RP 9下载既可 第三步: 注意:Axure RP 9 MAC正式版为苹果版本,Axure RP 9 WIN正式版为Windows版本 中文汉化包ÿ…...

腾讯云CVM服务器2核2g1m带宽支持多少人访问?
腾讯云2核2g1m的服务器支持多少人同时访问?2核2g1m云服务器短板是在1M公网带宽上,腾讯云服务器网以网站应用为例,当大规模用户同时访问网站时,很大概率会卡在公网带宽上,所以压根就谈不上2核2G的CPU内存计算性能是否够…...

8.12学习笔记
在PyTorch中,Dataset和DataLoader是用于处理数据的两个重要类。Dataset类是一个抽象类,用于表示数据集。它的主要作用是将数据加载到内存中,并提供一种统一的方式来访问数据。为了使用Dataset类,你需要继承它并实现两个方法&#…...

计算机体系中的不同的缓存存储层级说明
分级说明 L1缓存的标准延迟是4个周期。这意味着,当CPU请求数据时,L1缓存需要4个时钟周期来将数据传输给CPU。 L2缓存的标准延迟是12个周期。相对于L1缓存,L2缓存的容量更大,但其读取速度更慢,需要更多的时钟周期来传输…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
