当前位置： 首页 > news >正文

不同路径 II——力扣63

news 2026/2/10 12:06:14

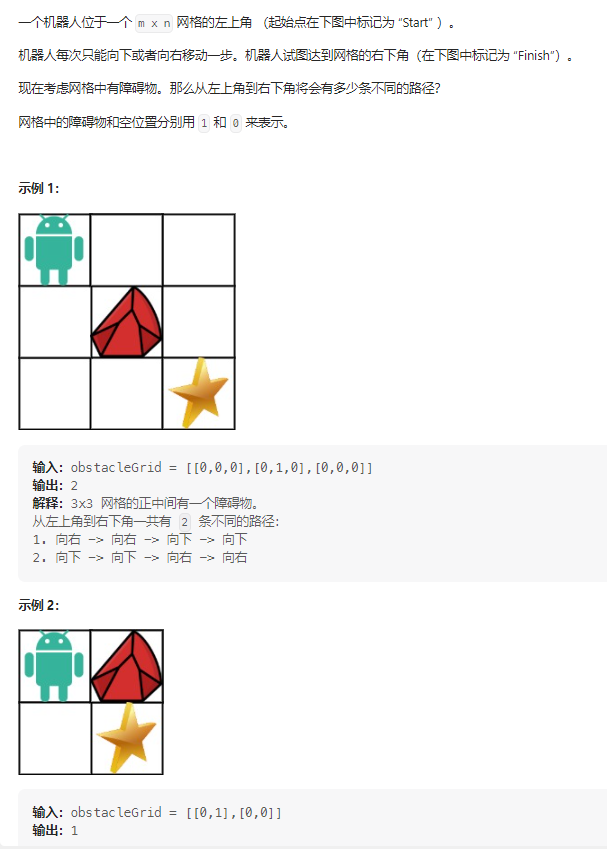
在这里插入图片描述
在这里插入图片描述

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int n=

相关文章：

不同路径 II——力扣63

class Solution {public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int n=...

编程日记 2023/8/13 22:29:59

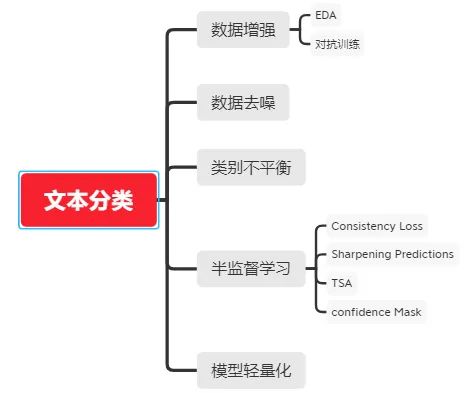
NLP文本分类

NLP文本分类 落地实战五大利器&#xff01;_kaiyuan_sjtu的博客-CSDN博客https://zhuanlan.zhihu.com/p/432619164 https://github.com/alibaba/EasyNLP/blob/master/README.cn.md...

编程日记 2023/8/13 22:28:58

进程和线程的联系与区别

文章目录 一、进程和线程的联系二、进程和线程的区别 一、进程和线程的联系 操作系统中可以有很多进程&#xff0c;每个进程都有自己独立的资源&#xff1b;一个进程中可以有很多线程&#xff0c;系统中的每个线程都能独立调度&#xff0c;同一个进程中的各个线程共享内存/硬盘…...

编程日记 2023/8/13 22:27:57

分支和循环语句（2）（C语言）

目录 do...while()循环 do语句的语法 do语句的特点 do while循环中的break和continue 练习 goto语句 do...while()循环 do语句的语法 do 循环语句; while(表达式); do语句的特点 循环至少执行一次&#xff0c;使用的场景有限&#xff0c;所以不是经常使用。 #inc…...

编程日记 2023/8/13 22:26:56

Flutter: A RenderFlex overflowed by 42 pixels on the bottom.

Flutter&#xff1a;渲染活动底部上方溢出了42个像素 Flutter 控件超出异常&#xff1a;A RenderFlex overflowed by 42 pixels on the bottom. 解决方案 1.Scaffold内添加 resizeToAvoidBottomInset 属性&#xff0c;缺点是软键盘下面的控件被挡住 Scaffold( resizeToAvoidBot…...

编程日记 2023/8/13 22:25:54

第三章，矩阵，07-用初等变换求逆矩阵、矩阵的LU分解

第三章&#xff0c;矩阵&#xff0c;07-用初等变换求逆矩阵、矩阵的LU分解 一个基本的方法求 A − 1 B A^{-1}B A−1BLU分解例1&#xff0c;求矩阵A的LU分解&#xff1a;例12&#xff0c;LU分解解线性方程组&#xff1a; 玩转线性代数(19)初等矩阵与初等变换的相关应用的笔记&a…...

编程日记 2023/8/13 22:24:52

STM32F429IGT6使用CubeMX配置SPI通信（W25Q256芯片）

1、硬件电路 需要系统性的看一下W25Q256芯片手册 2、设置RCC&#xff0c;选择高速外部时钟HSE,时钟设置为180MHz 3、配置SPI 4、生成工程配置 5、相关代码 #define sFLASH_ID 0XEF4019 // W25Q256#define SPI_FLASH_PageSize 256 #define SPI_FLASH_PerWritePageSize 256#def…...

编程日记 2023/8/13 22:23:50

C++11异步与通信之 packaged_task

概念简介 packaged_task 用于包装可调用目标(Callable)为一个对象,如lambda&#xff0c;普通函数&#xff0c;小括号重载等&#xff0c;用于异步调用。 其返回值或所抛异常被存储于能通过 std::future 对象访问的共享状态中&#xff0c;和promise类似。 将函数的调用与函数返…...

编程日记 2023/8/13 22:22:49

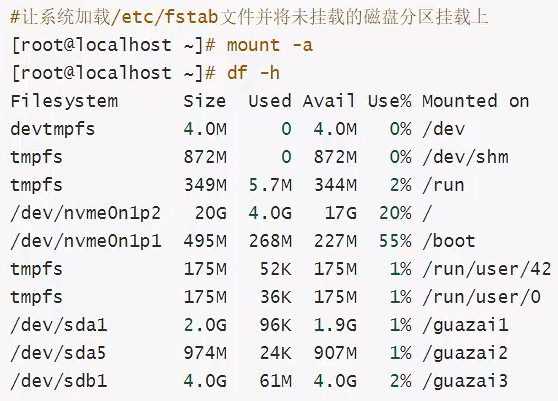
磁盘的管理

一、磁盘的分区 查看磁盘 lsblk fdisk -l 2、分区 没有e扩展&#xff0c;则都是主分区&#xff0c;已经有三个主分区了&#xff0c;剩下的全设置为扩展 查看分区结果&#xff1a; 二、格式化 三、挂载...

编程日记 2023/8/13 22:21:48

数据结构：完全二叉树的性质

完全二叉树的性质&#xff1a; 具有 n n n个结点的完全二叉树的深度为 [ l o g 2 n ] 1 ( [ x ] 表示不大于 x 的最大整数 ) [log_2n]1([x]表示不大于x的最大整数) [log2​n]1([x]表示不大于x的最大整数) 对于任意一个结点 &#xff08; 1 < i < n &#xff09; &…...

编程日记 2023/8/13 22:20:46

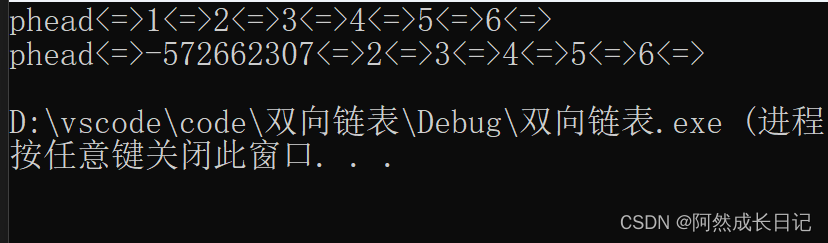
【数据结构】‘双向链表’冲冲冲

&#x1f490; &#x1f338; &#x1f337; &#x1f340; &#x1f339; &#x1f33b; &#x1f33a; &#x1f341; &#x1f343; &#x1f342; &#x1f33f; &#x1f344;&#x1f35d; &#x1f35b; &#x1f364; &#x1f4c3;个人主页 &#xff1a;阿然成长日记 …...

编程日记 2023/8/13 22:19:44

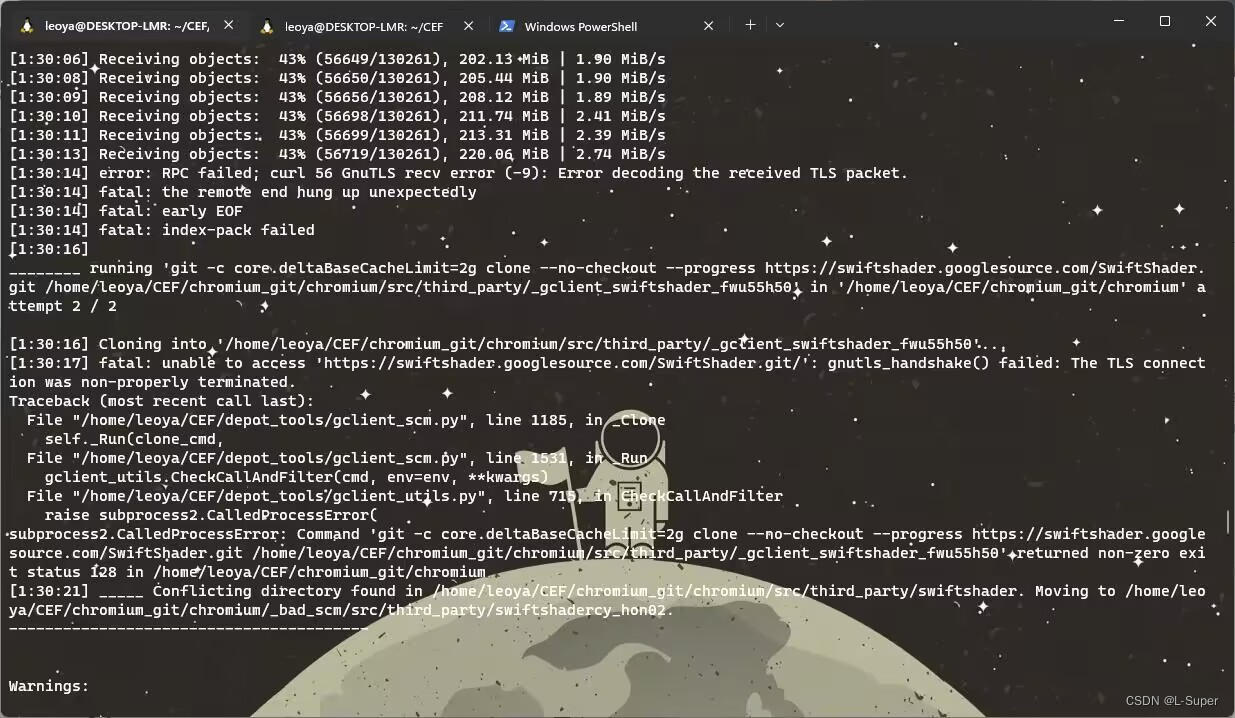
Linux 编译CEF源码详细记录

Linux CEF&#xff08;Chromium Embedded Framework&#xff09;源码下载编译 背景 由于CEF默认的二进制分发包不支持音视频播放&#xff0c;需要自行编译源码&#xff0c;将ffmpeg开关打开才能支持。这里介绍的是Linux平台下的CEF源码下载编译过程。 Windows平台参考&#…...

编程日记 2023/8/13 22:18:43

LeetCode 2810. Faulty Keyboard【模拟,双端队列,字符串】简单

本文属于「征服LeetCode」系列文章之一&#xff0c;这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁&#xff0c;本系列将至少持续到刷完所有无锁题之日为止&#xff1b;由于LeetCode还在不断地创建新题&#xff0c;本系列的终止日期可能是永远。在这一系列刷题文章…...

编程日记 2023/8/13 22:17:42

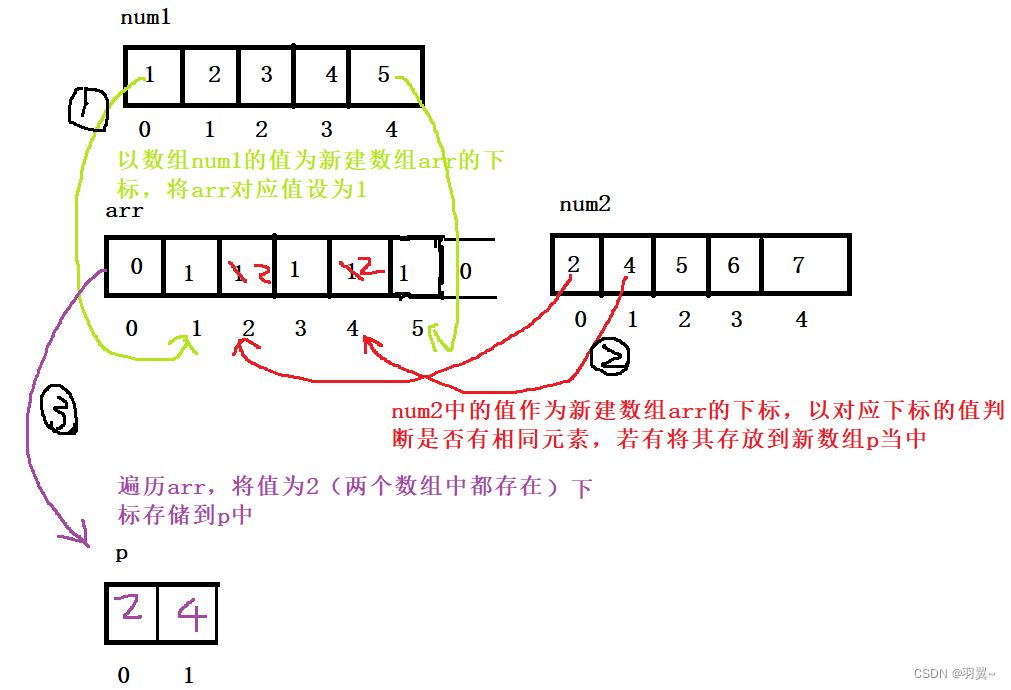
两个数组的交集-C语言/Java

描述 给定两个数组 nums1 和 nums2 &#xff0c;返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序。&#xff08;1 < nums1.length, nums2.length < 1000&#xff0c;0 < nums1[i], nums2[i] < 1000&#xff09; 示例1 输入…...

编程日记 2023/8/13 22:16:41

Arduino+esp32学习笔记

学习目标&#xff1a; 使用Arduino配置好蓝牙或者wifi模块 学习使用python配置好蓝牙或者wifi模块 学习内容&#xff08;笔记&#xff09;&#xff1a; 一、 Arduino语法基础 Arduino语法是基于C的语法,C又是c基础上增加了面向对象思想等进阶语言。那就只记录没见过的。 单多…...

编程日记 2023/8/13 22:15:40

计算机网络-专业术语

计算机网络-专业术语 实体 实体:任何可发送或接收信息的硬件或软件进程 对等实体:收发双方相同层次中的实体 协议 控制两个对等实体进行逻辑通信的规则的集合 协议三要素 语法 定义所交换的信息的格式 是用户数据与控制信息的结构和格式 语义 定义收发双方所需要完成的操作…...

编程日记 2023/8/13 22:14:39

E. Maximum Monogonosity

You are given an array aa of length nn and an array bb of length nn. The cost of a segment [l,r][l,r], 1≤l≤r≤n1≤l≤r≤n, is defined as |bl−ar||br−al||bl−ar||br−al|. Recall that two segments [l1,r1][l1,r1], 1≤l1≤r1≤n1≤l1≤r1≤n, and [l2,r2][l2,…...

编程日记 2023/8/13 22:13:37

已解决Excel file format cannot be determined, you must specify an engine manually

问题 我使用以下语句时出现错误 data pd.read_excel(temp_inputc.csv, headerNone)出现错误&#xff1a; Excel file format cannot be determined, you must specify an engine manually有很多人说添加engine&#xff0c;但接下来会出现这个错误&#xff1a; File is not…...

编程日记 2023/8/13 22:12:36

Centos yum命令大全

1.使用YUM查找软件包 $ yum search python 2.列出所有可安装的软件包 $ yum list | grep python 3.列出所有可更新的软件包 $ yum list updates 4.列出所有已安装的软件包 $ yum list installed | grep python...

编程日记 2023/8/13 22:11:35

内网横向移动—ARP攻击图片捕捉数据劫持DNS劫持

内网横向移动—ARP攻击&图片捕捉&数据劫持&DNS劫持 1. ARP1.1. APR介绍1.1.1. ARP工作原理1.1.2. APR欺骗工作原理 1.2. 环境准备1.3. 适用场景 2. ARP断网攻击演示2.1. 使用kali进行演示2.1.1. nmap判断存活2.1.2. 安装工具2.1.3. 攻击Windows 10虚拟机2.1.3.1. 查…...

编程日记 2023/8/13 22:10:32

Python爬虫实战：研究MechanicalSoup库相关技术

一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库，专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力，提供了直观的 API，让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

编程新知 2025/10/10 18:13:55

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法

树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源&#xff1a; http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作&#xff0c;无需更改相机配置。但是&#xff0c;一…...

编程新知 2026/2/5 4:39:03

spring：实例工厂方法获取bean

spring处理使用静态工厂方法获取bean实例&#xff0c;也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下&#xff1a; 定义实例工厂类&#xff08;Java代码&#xff09;&#xff0c;定义实例工厂&#xff08;xml&#xff09;&#xff0c;定义调用实例工厂&#xff…...

编程新知 2025/11/25 22:46:30

JVM暂停（Stop-The-World，STW）的原因分类及对应排查方案

JVM暂停（Stop-The-World，STW）的完整原因分类及对应排查方案，结合JVM运行机制和常见故障场景整理而成： 一、GC相关暂停​​ 1. ​​安全点（Safepoint）阻塞​​ ​​现象​​：JVM暂停但无GC日志，日志显示No GCs detected。​​原因​​：JVM等待所有线程进入安全点（如…...

编程新知 2026/2/7 11:25:15

深度学习习题2

1.如果增加神经网络的宽度&#xff0c;精确度会增加到一个特定阈值后&#xff0c;便开始降低。造成这一现象的可能原因是什么&#xff1f; A、即使增加卷积核的数量&#xff0c;只有少部分的核会被用作预测 B、当卷积核数量增加时&#xff0c;神经网络的预测能力会降低 C、当卷…...

编程新知 2026/1/26 5:53:30

Git 3天2K星标：Datawhale 的 Happy-LLM 项目介绍（附教程）

引言 在人工智能飞速发展的今天&#xff0c;大语言模型&#xff08;Large Language Models, LLMs&#xff09;已成为技术领域的焦点。从智能写作到代码生成&#xff0c;LLM 的应用场景不断扩展&#xff0c;深刻改变了我们的工作和生活方式。然而&#xff0c;理解这些模型的内部…...

编程新知 2026/1/29 11:06:33

Git常用命令完全指南：从入门到精通

Git常用命令完全指南&#xff1a;从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

编程新知 2025/10/3 0:40:01

Vue ③-生命周期 || 脚手架

生命周期 思考&#xff1a;什么时候可以发送初始化渲染请求&#xff1f;&#xff08;越早越好&#xff09; 什么时候可以开始操作dom&#xff1f;&#xff08;至少dom得渲染出来&#xff09; Vue生命周期&#xff1a; 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

编程新知 2026/2/5 5:24:23

【LeetCode】算法详解#6 ---除自身以外数组的乘积

1.题目介绍 给定一个整数数组 nums&#xff0c;返回 数组 answer &#xff0c;其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法&#xff0c;且在 O…...

编程新知 2026/2/9 9:22:40

Spring Security 认证流程——补充

一、认证流程概述 Spring Security 的认证流程基于 过滤器链&#xff08;Filter Chain&#xff09;&#xff0c;核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤&#xff1a; 用户提交登录请求拦…...

编程新知 2026/2/4 17:50:55