OptaPlanner笔记1
1.1 什么是OptaPlanner
每个组织都面临规划问题:为产品或服务提供有限的受约束的资源(员工、资产、时间和金钱)。OptaPlanner用来优化这种规划,以实现用更少的资源来做更多的业务。 这被称为Constraint Satisfaction Programming(约束规划,这是运筹学学科的一部分)。
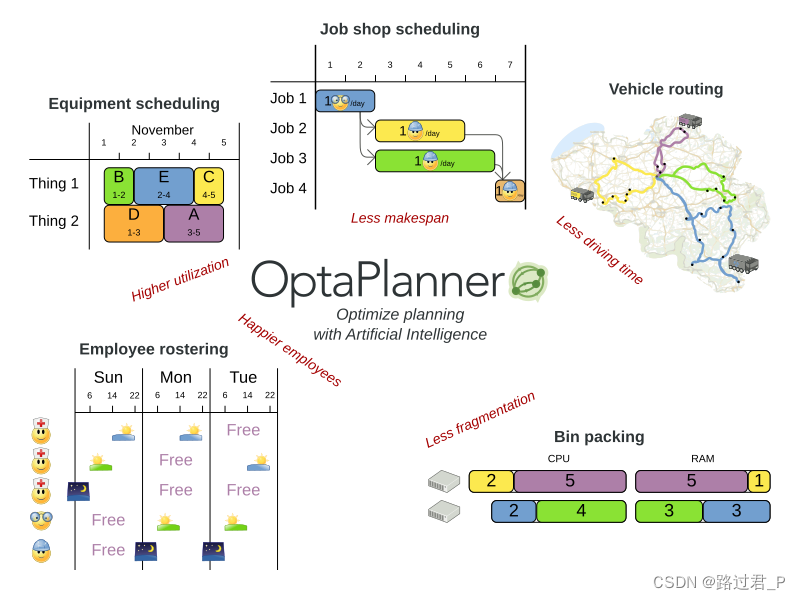
OptaPlanner 是一个轻量级、可嵌入的约束满足问题求解引擎,可优化规划问题。它适用的场景例如:
- 员工轮班排班:为护士、修理工等排班。
- 议程安排:安排会议,约会,维护工作,广告等。
- 教育方面的排班:安排学科,课程,考试,学术会议等。
- 车辆路线:利用已知的地图工具规划运输货物和/或乘客的车辆路线,这些路线可以经过多个目的地。
- 装箱问题:如何使用装箱、卡车、船舶和存储仓库装载物品,或者是云计算中如何跨计算机资源打包信息。
- 车间作业调度:汽车装配线规划、机器队列规划、劳动力任务规划等。
- 切割库存:在切割纸张、钢材、地毯等时最大限度地减少浪费。
- 体育日程安排:为足球联赛、棒球联赛规划比赛和训练时间表。
- 财务优化:投资组合优化、风险分散等。
1.2 什么是规划问题

规划问题存在一个基于有限资源和特定规则的最优解。最优解可以是任何数量的事务,例如:
- 利润最大化
- 环境影响最小化
- 员工和顾客满意度最大化
实现这些目标的能力取决于可用资源的数量,例如:
- 人员数量
- 时间
- 预算
- 实物资产(机械、车辆、计算机、建筑物等)
还必须考虑与这些资源相关的特定限制,例如一个人的工作小时数、他们使用某些机器的能力或设备之间的兼容性。
OptaPlanner可以帮助Java程序员有效地解决约束满足问题。它使用非常有效的得分计算,将优化启发式和元启发式算法结合在一起。
1.2.1 规划问题是NP-Complete还是NP-Hard问题
NP-Hard问题是指在多项式时间内无法解决的问题。这些问题通常是非常困难的,因为它们的解决需要大量的计算资源。NP-Hard问题的例子包括旅行推销员问题、分治问题等。
NP-Complete问题是指在多项式时间内可以解决,但在NP-Hard问题的解决过程中可以被解决的问题。这些问题的解决通常比NP-Hard问题的解决要快,但仍然需要大量的计算资源。NP-Complete问题的例子包括完全背包问题、分支界限问题等。
前面提到的所有场景都可能是NP-Complete或者NP-Hard的,也就是说:
- 在合理的时间内验证问题的给定解决方案很容易。
- 没有灵丹妙药可以在合理的时间内找到问题的最佳解决方案。(至少,世界上最聪明的计算机科学家还没有发现这样的灵丹妙药。 但是,如果他们找到一个适用于某个NP-Complete问题的解决方案,它将适用于每个NP-Complete问题。)
这意味着解决问题可能比你预期的要困难,因为常用的技术不足以解决问题:
- 蛮力算法(即使是再聪明的变体)将会耗费大量的时间
- 快速算法(例如在装箱问题中,先放入最大的物品)将得到远远偏离最优解的解决方案。
通过使用先进的优化算法,OptaPlanner 可以在合理的时间内为这类规划问题找到接近最优的解决方案。
1.2.2 规划问题存在约束(硬约束或软约束)
通常,规划问题存在至少两个级别的约束:
- 绝对不可破坏的(负面)硬约束。(例如,一名教师不能同时教授两节不同的课程。)
- 如果可以避免,就不应该破坏的(负面)软约束。(例如:某教师不喜欢在星期五的下午授课。)
某些问题也可能存在积极的约束:
- 如果可能的话,应该满足的(正向的)软约束。(例如,某教师喜欢在星期一的上午授课。)
某些基础问题(例如N皇后问题)只存在硬约束。某些问题存在三个或更多级别的约束,例如硬、中等、软约束。
这些约束定义了规划问题的得分计算(也称为适应度函数)。规划问题的每个解决方案都可以用得分评级。在 OptaPlanner 中,得分约束用面向对象的语言(例如Java代码)编写。这样的代码易于编写、灵活且可扩展。
1.2.3 规划问题存在巨大的搜索空间
规划问题有许多解决方案。 这些解决方案可划分为以下几类:
- 不考虑是否破坏任何约束的possible solution(可能方案)。规划问题往往存在大量这种毫无价值的解决方案。
- 不破坏任何负面硬约束的feasible solution(可行方案)。可行方案往往与可能方案数量相对。有时候没有可行方案。每一个可行方案都是可能方案
- 得分最高的optimal solution(最佳方案)。规划问题至少有一个最佳方案。即使没有可行方案,且最佳方案不可行的情况下也是如此。
- 在给定时间内找到的最高分的best solution(最优方案)。最优方案可能是可行的,如果时间充裕的话,它就是最佳方案。
与直觉相反,即使数据集很小,可能方案的数量也是巨大的(如果计算正确的话)。正如你在例子中看到的,大多数案例比已知宇宙中原子的数量(10^80)有更多的可能方案。由于没有找到最优解决方案的灵丹妙药,因此任何实现都必须评估一部分的可能方案。
OptaPlanner支持多种优化算法,可以有效地处理大量可能方案。 根据用例的不同,某些优化算法的性能优于其他算法,但无法提前判断。使用 OptaPlanner,只需几行XML或代码来修改求解器的配置,即可轻松切换优化算法。
相关文章:

OptaPlanner笔记1
1.1 什么是OptaPlanner 每个组织都面临规划问题:为产品或服务提供有限的受约束的资源(员工、资产、时间和金钱)。OptaPlanner用来优化这种规划,以实现用更少的资源来做更多的业务。 这被称为Constraint Satisfaction Programming…...

github 镜像站及下载加速网址
1、提供常用的镜像网址(记住千万别登录账号): https://github.com.cnpmjs.org https://hub.fastgit.org https://hub.nuaa.cf/ https://hub.yzuu.cf/ https://hub.njuu.cf/上面的网址是一个克隆版的Github,上面的镜像网站内容跟G…...
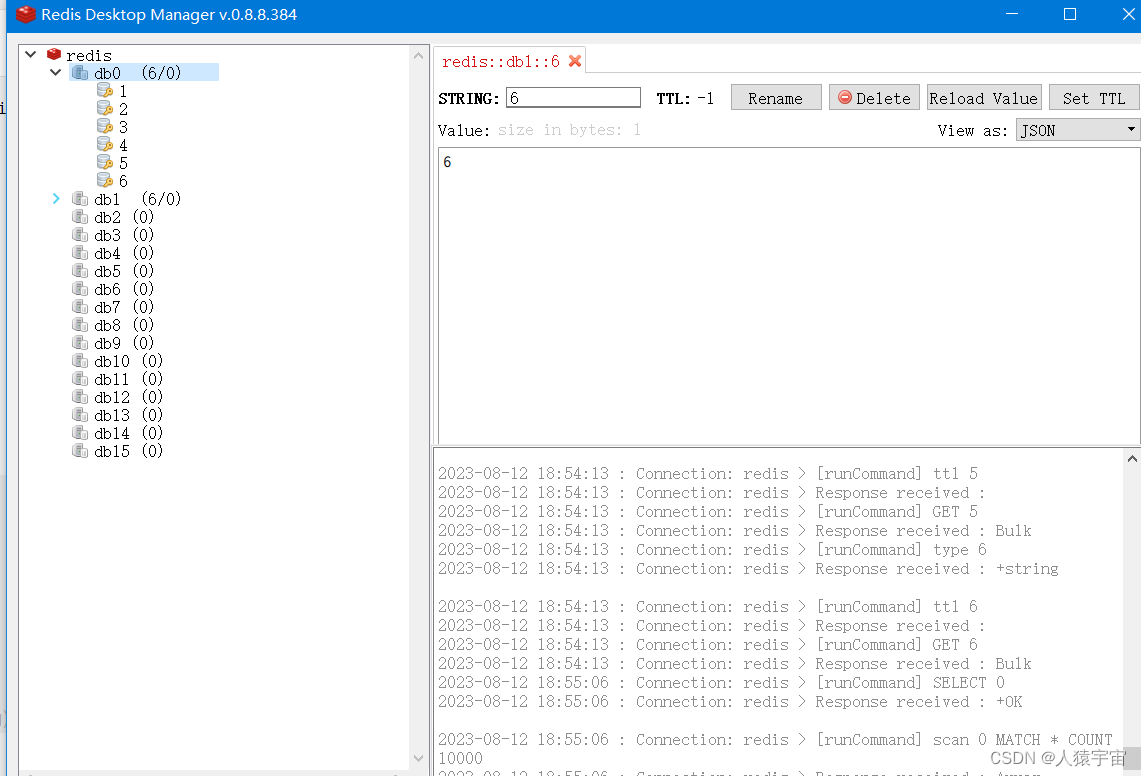
大数据-玩转数据-Flink RedisSink
一、添加Redis Connector依赖 具体版本根据实际情况确定 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-redis_2.11</artifactId><version>1.1.5</version> </dependency>二、启动redis 参…...
)
c++病毒/恶搞代码大全( 上 )
注:以下代码应勿用于非法(Dev-c5.11实测可用) 1: 效果:无限生成cmd 解决方法:关闭程序即可 #include<bits/stdc.h> #include<windows.h> using namespace std; int main() {while(1)system("start cmd"…...
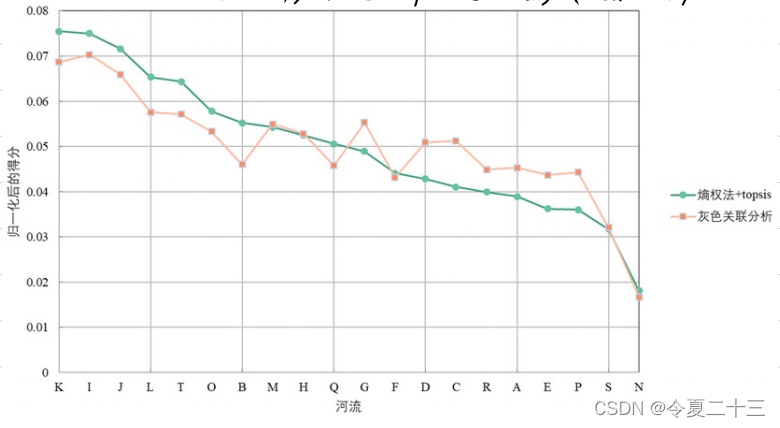
【数学建模】清风数模更新5 灰色关联分析
灰色关联分析综述 诸如经济系统、生态系统、社会系统等抽象系统都包含许多因素,系统整体的发展受各个因素共同影响。 为了更好地推动系统发展,我们需要清楚哪些因素是主要的,哪些是次要的,哪些是积极的,哪些是消极的…...

Windows下运行Tomcat服务时报GC Overhead Limit Exceeded
根本原因是在新建Tomcat作为Windows服务时,系统默认设置的堆内存太小了,我们打开/bin/service.bat文件,将如下图所示的默认值改大一些就好了 if "%JvmMs%" "" set JvmMs512 if "%JvmMx%" "" set J…...
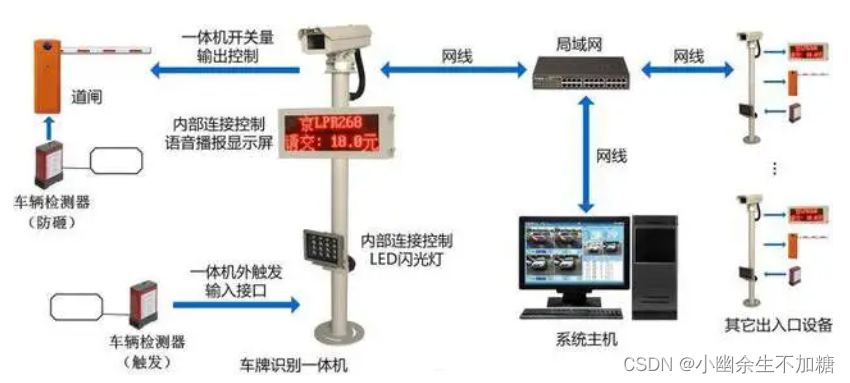
OpenCV实例(八)车牌字符识别技术(一)模式识别
车牌字符识别技术(一)模式识别 1.模式识别流程2. 模式识别方式 影响并导致汽车牌照内字符出现缺损、污染、模糊等情况的常见因素有照相机的性能、采集车辆图像时光照的差异、汽车牌照的清洁度等。为了提高汽车牌照字符识别的准确率,本节将把英…...
霍夫线检测+找出轮廓和外接矩形+改进旋转)
OPENCV C++(七)霍夫线检测+找出轮廓和外接矩形+改进旋转
霍夫线检测 vector<Vec2f> lines1;HoughLines(canny_mat, lines1, 1, CV_PI / 180.0,90 );//45可以检测里面两条线 80检测出外边两条线 定义存放输出线的向量 此向量输出有<距离,角度> 因为检测的原理就是在变换霍夫空间里面去检测的,这里可…...
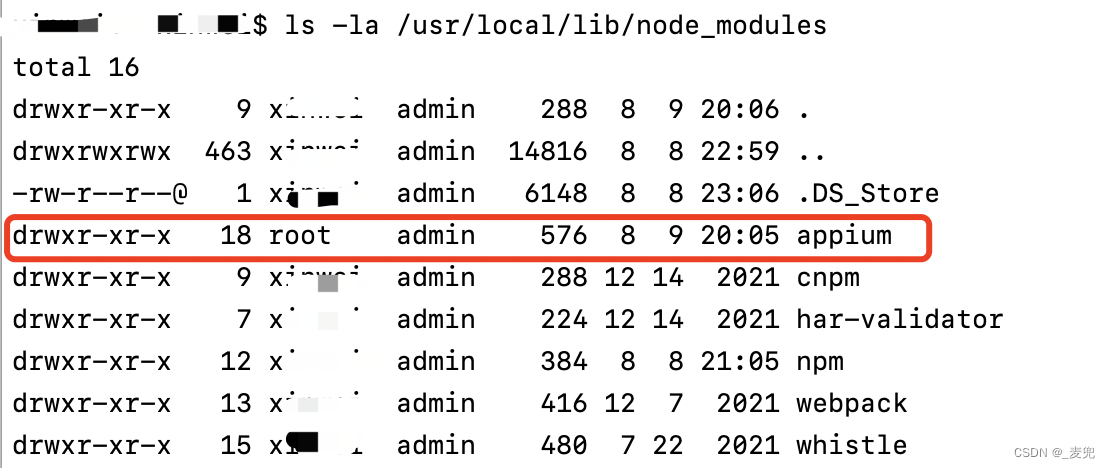
Error: EACCES: permission denied, rename ‘/usr/local/lib/node_modules/appium‘
在使用npm uninstall -g appium卸载appium的过程中报错 Error: EACCES: permission denied, rename /usr/local/lib/node_modules/appium -> /usr/local/lib/node_modules/.appium-cfBVovI6 npm ERR! code EACCES npm ERR! syscall rename npm ERR! path /usr/local/lib/n…...
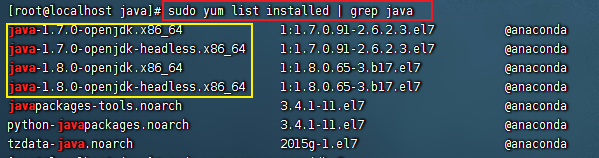
CentOS 7中,配置了Oracle jdk,但是使用java -version验证时,出现的版本是OpenJDK,如何解决?
1.首先,检查已安装的jdk版本 sudo yum list installed | grep java2.移除、卸载圈红的系统自带的openjdk sudo yum remove java-1.7.0-openjdk.x86_64 sudo yum remove java-1.7.0-openjdk-headless.x86_64 sudo yum remove java-1.8.0-openjdk.x86_64 sudo yum r…...
)
牛客 松鼠回家(二分答案+最短路)
题目描述 松鼠宝宝由于贪玩去了一个具有n个点和m条边的无向图中,现在松鼠宝宝仅有h点体力,所有的边经过一次后会消耗部分体力,同时松鼠爸爸为了惩罚贪玩的松鼠宝宝,每到一个点会扣除部分松果(起点的松果也会扣除&#…...
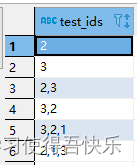
Mysql in 查询的奇怪方向
Mysql in 查询的奇怪方向 关于表字段存储的数据为 num1,num2,num3时, 还要通过多个num1,num2入参针对该字段进行查询 建表语句 CREATE TABLE test (test_ids varchar(100) DEFAULT NULL COMMENT 保存ids 以逗号分隔 ) ENGINEInnoDB;数据项 查询语句 SELECT test_ids FROM t…...
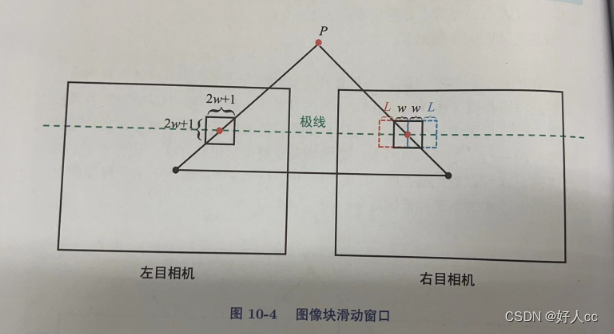
ORB-SLAM2第二节---双目地图初始化
比起单目初始化,而双目实现地图的初始化非常简单,只需要一帧(左右目图像)即可完成初始化。 行特征点统计。考虑用图像金字塔尺度作为偏移量,在当前点上下正负偏移量(r)内的纵坐标值都认为是匹配点可能存在…...

后端常使用的中间件知识点--持续更新
类型难度mysqlmysql中SQL优化:多角度分析包学包会,sql优化全过程,刨根分析redis多角度剖析redis数据结构及底层实现原理、应用场景MQ简单大体说明RabbitMQ的使用(简单版)mybatis使用JDBC的批量插入百万数据要多少秒一遍…...

非科班的大家如何顺滑转码
近年来,很多人想要从其他行业跳槽转入计算机领域。非计算机科班如何丝滑转码?请来聊聊你的看法和观点,我本身是信息与计算科学专业,周围的同学有不少也是被这个名字“骗过来的”,看这个名字都以为是计算机相关专业&…...

webpack中常见的Loader
目录 1.webpack中的loader是什么?配置方式 2. loader特性3.常见的loader 1.webpack中的loader是什么? loader 用于对模块的"源代码"进行转换,在 import 或"加载"模块时预处理文件 webpack做的事情,仅仅是分…...
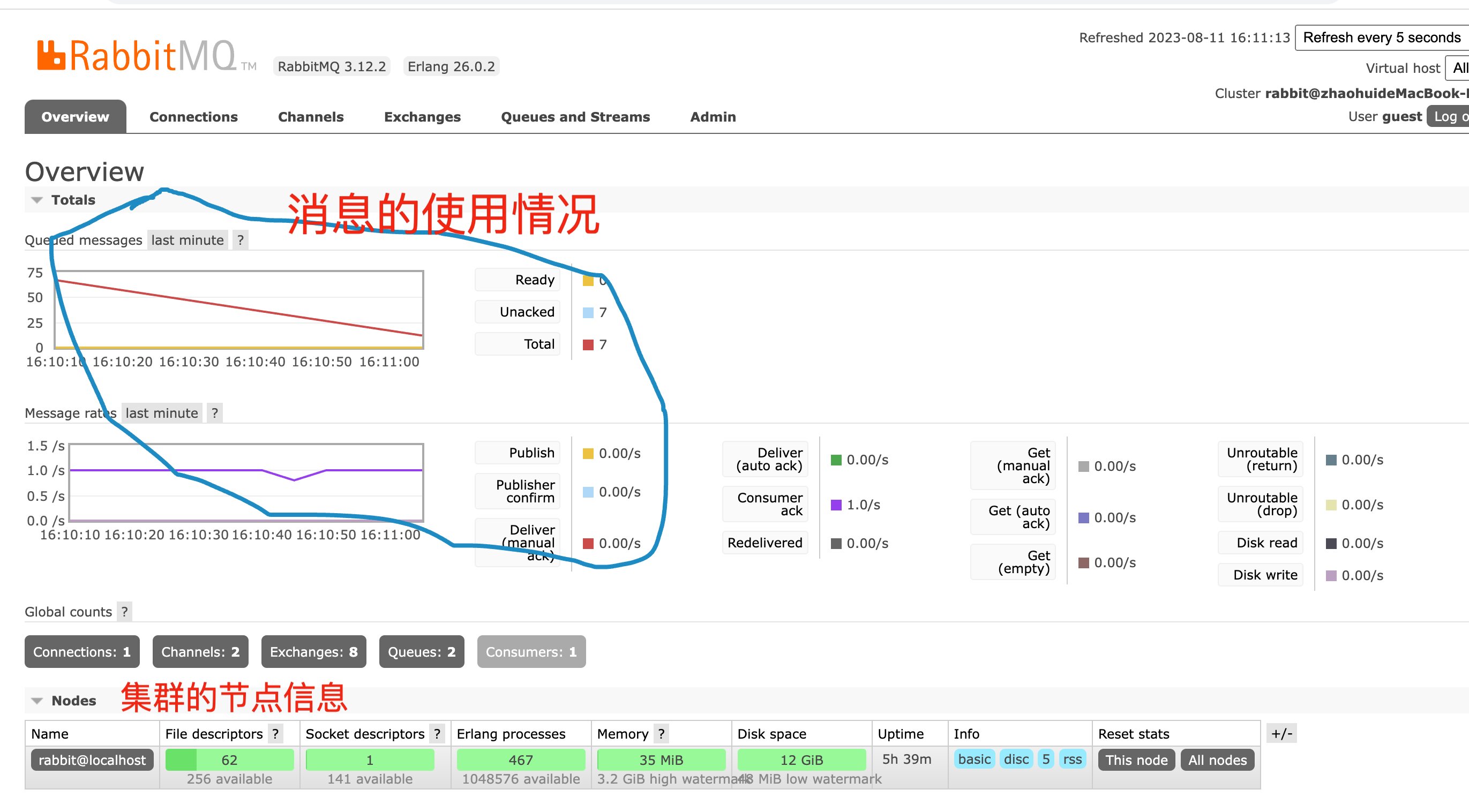
RabbitMQ:可靠消息传递的强大消息中间件
消息中间件在现代分布式系统中起着关键作用,它们提供了一种可靠且高效的方法来进行异步通信和解耦。在这篇博客中,我们将重点介绍 RabbitMQ,一个广泛使用的开源消息中间件。我们将深入探讨 RabbitMQ 的特性、工作原理以及如何在应用程序中使用…...

python 批量下载m3u8的视频
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:点击跳转 方法: 解析m3u8,获取其中的ts列表,多线程下载所有ts文件。 全部下完之后,用ffmpeg合…...

最后一击
第二届上海市青少年算法竞赛(小学组) 题目描述 Description 小爱和小艾两人组队打一只怪兽。一开始怪兽有 n 点生命值,当 n 变成 0 或更低时,怪兽就被消灭了。他们两人是同时开始攻击的,小爱每分钟可以攻击 a 下&…...

K8S资源管理方式
K8S资源管理方式 文章目录 K8S资源管理方式一、陈述式资源管理1.基础命令操作2.创建pod3.查看资源状态4.查看pod中的容器日志5.进入pod中的容器6.删除pod资源7.pod扩容8.项目生命周期管理(创建-->发布-->更新-->回滚-->删除)8.1创建services…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
