【数学建模】清风数模更新5 灰色关联分析
灰色关联分析综述
诸如经济系统、生态系统、社会系统等抽象系统都包含许多因素,系统整体的发展受各个因素共同影响。
为了更好地推动系统发展,我们需要清楚哪些因素是主要的,哪些是次要的,哪些是积极的,哪些是消极的,这就要求我们进行系统分析。
数理统计中的系统分析方法包括回归分析、方差分析和主成分分析,它们都存在一些不足之处,当数据样本较少时,灰色关联分析方法可以较好地克服那些不足。
因此,当样本个数较大时,一般使用标准化回归;当样本个数较少时,才使用灰色关联分析。
灰色关联分析的基本思想,是根据序列曲线的几何形状的相似程度来判断其联系是否紧密,曲线越接近,相似序列之间的关联度就越大,反之就越小。
接下来我们用两个例题来介绍一下灰色关联分析的两种应用。
应用一:进行系统分析

第一步:画统计图并分析
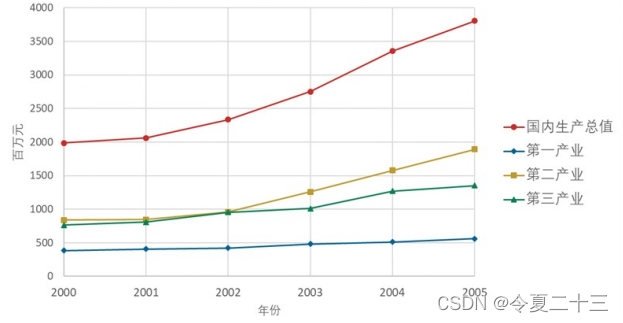
由图可知:
- 四个变量均呈上升趋势;
- 第二产业的增幅较为明显;
- 第二产业和第三产业的差距在后三年相差更大。
第二步:确定分析数列
母序列(参考数列、母指标):能反映系统行为特征的数据序列。类似于因变量Y,这里记作X0
子序列(比较序列、子指标):影响系统行为的因素组成的数据序列。类似于自变量X,记作X1~Xn
在例题中,国内生产总值就是母序列,第一、第二和第三产业就是子序列。
第三步:对变量进行预处理
目的:去量纲,缩小变量范围以简化计算。
对母序列和子序列中的每个指标进行预处理:先求出每个指标的均值,再用该指标的每个元素除以其均值。
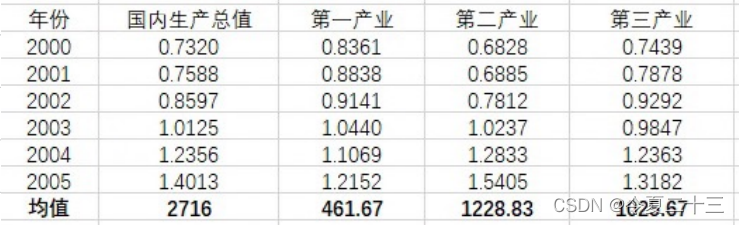
第四步:计算子序列中各个指标与母序列的关联系数
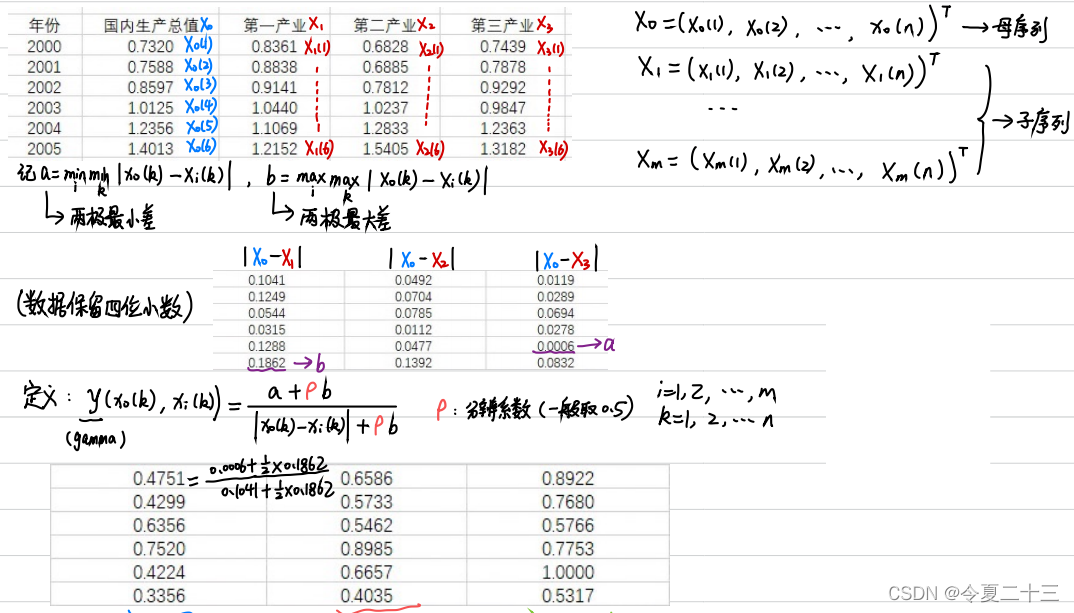
第五步:求出灰色关联度
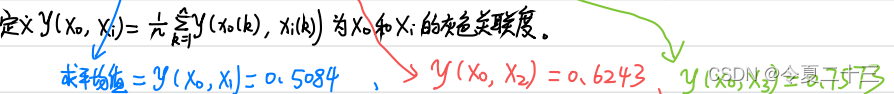
第六步:比较关联度,得出结论
对这个例题来说,该地区在2000年至2005年间的国内生产总值受到第三产业的影响最大(其灰色关联度最大)。
代码
clear;clc
load gdp.mat % 导入数据 一个6*4的矩阵
Mean = mean(gdp); % 求出每一列的均值以供后续的数据预处理
gdp = gdp ./ repmat(Mean,size(gdp,1),1); %size(gdp,1)=6, repmat(Mean,6,1)可以将矩阵进行复制,复制为和gdp同等大小,然后使用点除(对应元素相除)
disp('预处理后的矩阵为:'); disp(gdp)
Y = gdp(:,1); % 母序列
X = gdp(:,2:end); % 子序列
absX0_Xi = abs(X - repmat(Y,1,size(X,2))) % 计算|X0-Xi|矩阵(在这里我们把X0定义为了Y)
a = min(min(absX0_Xi)) % 计算两级最小差a
b = max(max(absX0_Xi)) % 计算两级最大差b
rho = 0.5; % 分辨系数取0.5
gamma = (a+rho*b) ./ (absX0_Xi + rho*b) % 计算子序列中各个指标与母序列的关联系数
disp('子序列中各个指标的灰色关联度分别为:')
disp(mean(gamma))
应用二:综合评价问题
题目:评价下表中20条河流的水质情况。(用Topsis结合熵权法也可以解决)
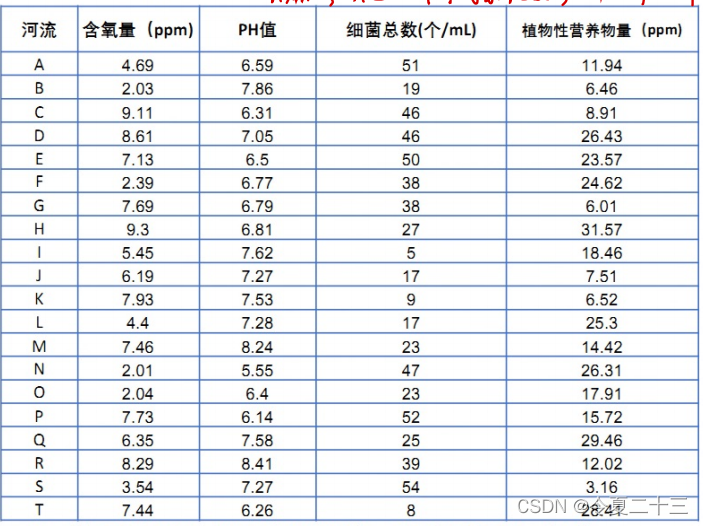
解题步骤
- 对指标正向化
- 对正向化后的矩阵进行预处理
- 将预处理后的矩阵每一行取出最大值构成母序列
- 计算各个指标与母序列的灰色关联度
- 计算各个指标灰色关联度的权重
- 计算各个评价对象的得分(用权重计算)
- 对得分进行归一化
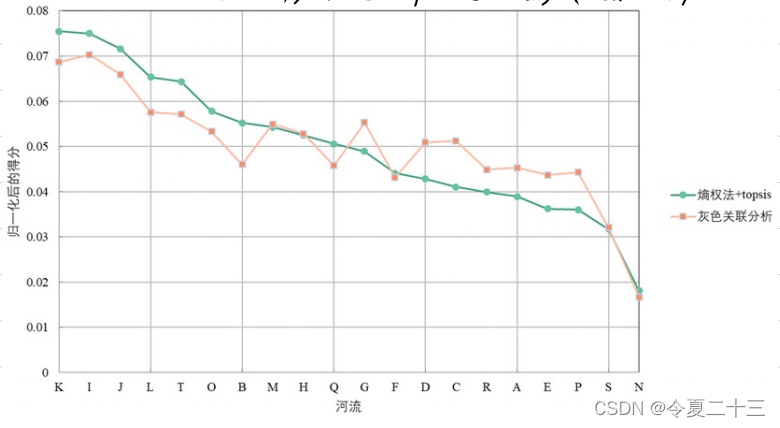
相关文章:

【数学建模】清风数模更新5 灰色关联分析
灰色关联分析综述 诸如经济系统、生态系统、社会系统等抽象系统都包含许多因素,系统整体的发展受各个因素共同影响。 为了更好地推动系统发展,我们需要清楚哪些因素是主要的,哪些是次要的,哪些是积极的,哪些是消极的…...

Windows下运行Tomcat服务时报GC Overhead Limit Exceeded
根本原因是在新建Tomcat作为Windows服务时,系统默认设置的堆内存太小了,我们打开/bin/service.bat文件,将如下图所示的默认值改大一些就好了 if "%JvmMs%" "" set JvmMs512 if "%JvmMx%" "" set J…...
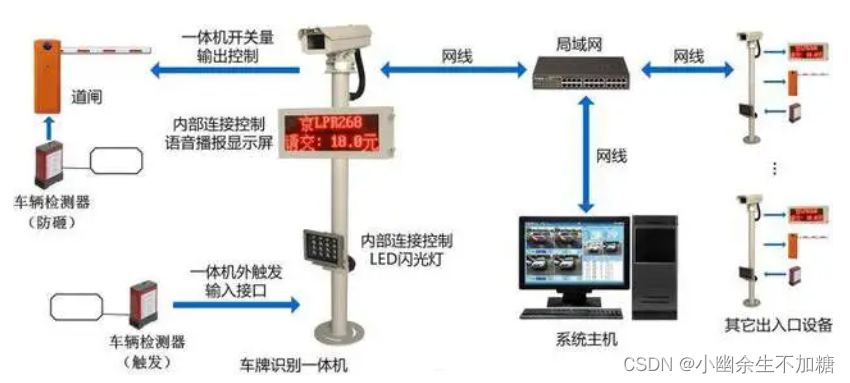
OpenCV实例(八)车牌字符识别技术(一)模式识别
车牌字符识别技术(一)模式识别 1.模式识别流程2. 模式识别方式 影响并导致汽车牌照内字符出现缺损、污染、模糊等情况的常见因素有照相机的性能、采集车辆图像时光照的差异、汽车牌照的清洁度等。为了提高汽车牌照字符识别的准确率,本节将把英…...
霍夫线检测+找出轮廓和外接矩形+改进旋转)
OPENCV C++(七)霍夫线检测+找出轮廓和外接矩形+改进旋转
霍夫线检测 vector<Vec2f> lines1;HoughLines(canny_mat, lines1, 1, CV_PI / 180.0,90 );//45可以检测里面两条线 80检测出外边两条线 定义存放输出线的向量 此向量输出有<距离,角度> 因为检测的原理就是在变换霍夫空间里面去检测的,这里可…...
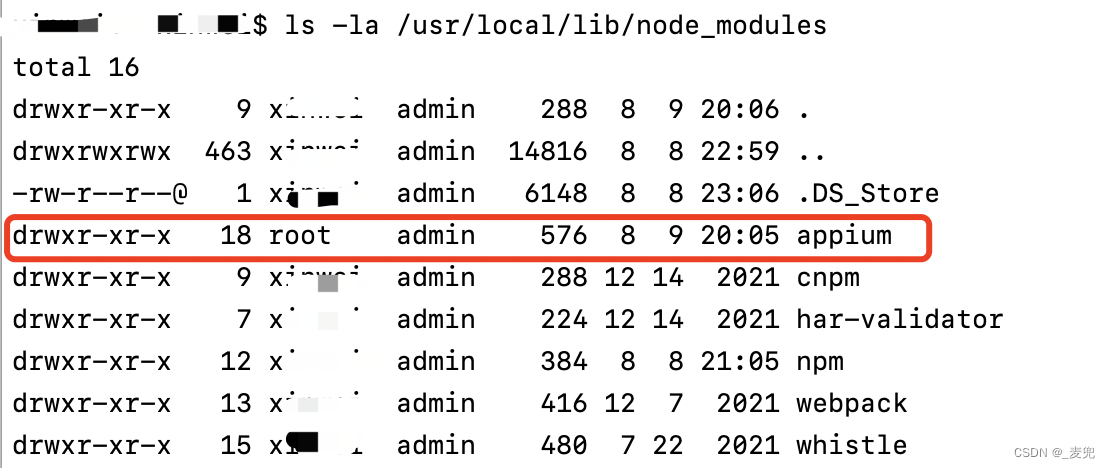
Error: EACCES: permission denied, rename ‘/usr/local/lib/node_modules/appium‘
在使用npm uninstall -g appium卸载appium的过程中报错 Error: EACCES: permission denied, rename /usr/local/lib/node_modules/appium -> /usr/local/lib/node_modules/.appium-cfBVovI6 npm ERR! code EACCES npm ERR! syscall rename npm ERR! path /usr/local/lib/n…...
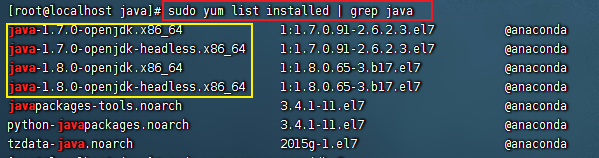
CentOS 7中,配置了Oracle jdk,但是使用java -version验证时,出现的版本是OpenJDK,如何解决?
1.首先,检查已安装的jdk版本 sudo yum list installed | grep java2.移除、卸载圈红的系统自带的openjdk sudo yum remove java-1.7.0-openjdk.x86_64 sudo yum remove java-1.7.0-openjdk-headless.x86_64 sudo yum remove java-1.8.0-openjdk.x86_64 sudo yum r…...
)
牛客 松鼠回家(二分答案+最短路)
题目描述 松鼠宝宝由于贪玩去了一个具有n个点和m条边的无向图中,现在松鼠宝宝仅有h点体力,所有的边经过一次后会消耗部分体力,同时松鼠爸爸为了惩罚贪玩的松鼠宝宝,每到一个点会扣除部分松果(起点的松果也会扣除&#…...
Mysql in 查询的奇怪方向
Mysql in 查询的奇怪方向 关于表字段存储的数据为 num1,num2,num3时, 还要通过多个num1,num2入参针对该字段进行查询 建表语句 CREATE TABLE test (test_ids varchar(100) DEFAULT NULL COMMENT 保存ids 以逗号分隔 ) ENGINEInnoDB;数据项 查询语句 SELECT test_ids FROM t…...
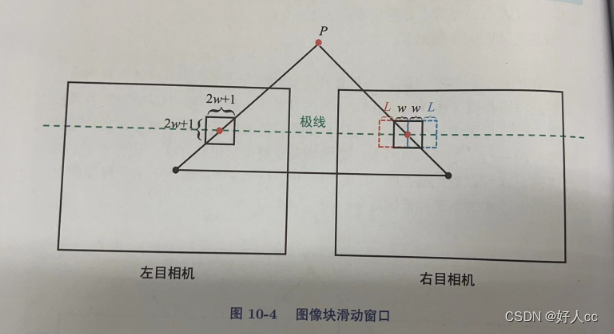
ORB-SLAM2第二节---双目地图初始化
比起单目初始化,而双目实现地图的初始化非常简单,只需要一帧(左右目图像)即可完成初始化。 行特征点统计。考虑用图像金字塔尺度作为偏移量,在当前点上下正负偏移量(r)内的纵坐标值都认为是匹配点可能存在…...

后端常使用的中间件知识点--持续更新
类型难度mysqlmysql中SQL优化:多角度分析包学包会,sql优化全过程,刨根分析redis多角度剖析redis数据结构及底层实现原理、应用场景MQ简单大体说明RabbitMQ的使用(简单版)mybatis使用JDBC的批量插入百万数据要多少秒一遍…...

非科班的大家如何顺滑转码
近年来,很多人想要从其他行业跳槽转入计算机领域。非计算机科班如何丝滑转码?请来聊聊你的看法和观点,我本身是信息与计算科学专业,周围的同学有不少也是被这个名字“骗过来的”,看这个名字都以为是计算机相关专业&…...

webpack中常见的Loader
目录 1.webpack中的loader是什么?配置方式 2. loader特性3.常见的loader 1.webpack中的loader是什么? loader 用于对模块的"源代码"进行转换,在 import 或"加载"模块时预处理文件 webpack做的事情,仅仅是分…...
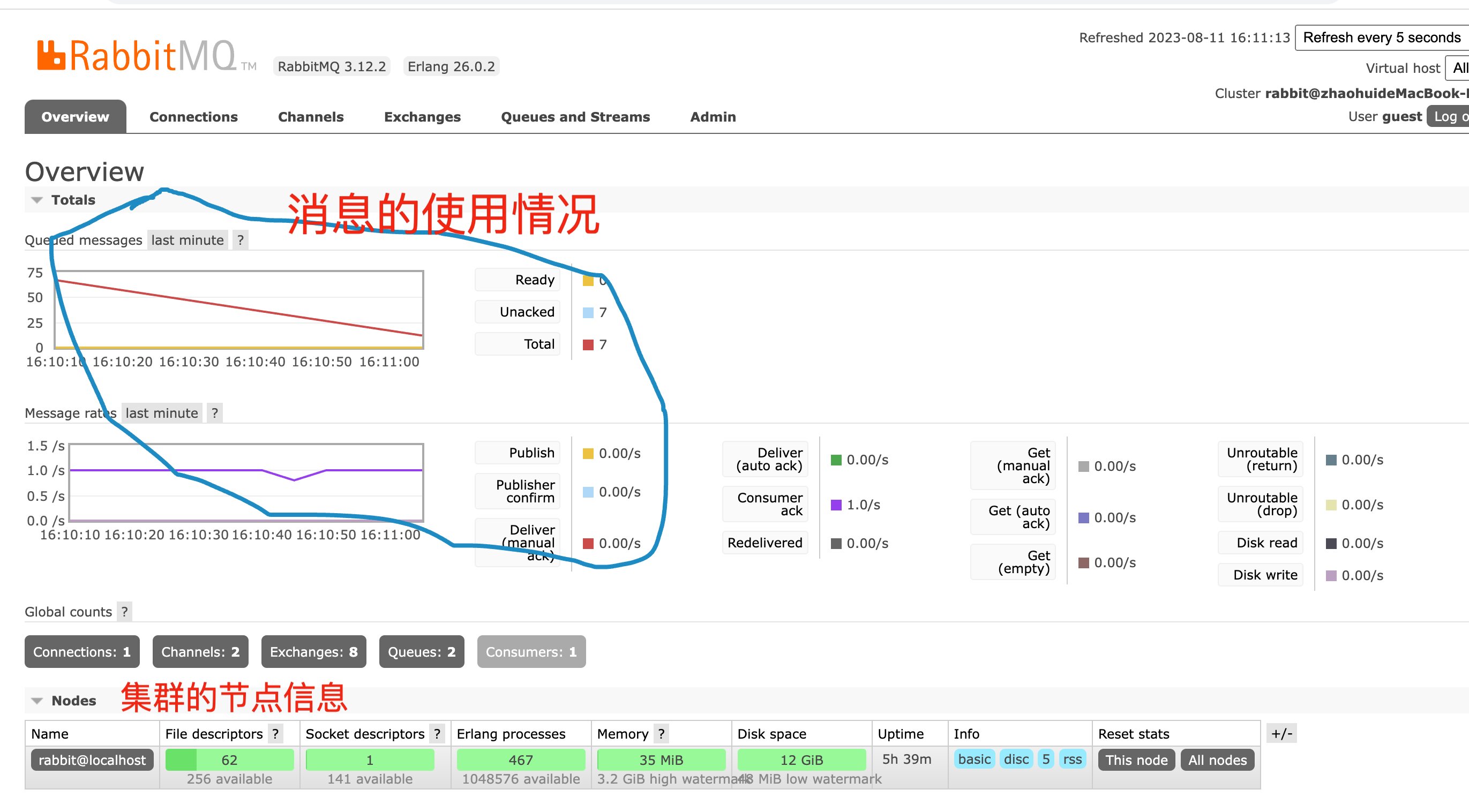
RabbitMQ:可靠消息传递的强大消息中间件
消息中间件在现代分布式系统中起着关键作用,它们提供了一种可靠且高效的方法来进行异步通信和解耦。在这篇博客中,我们将重点介绍 RabbitMQ,一个广泛使用的开源消息中间件。我们将深入探讨 RabbitMQ 的特性、工作原理以及如何在应用程序中使用…...

python 批量下载m3u8的视频
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:点击跳转 方法: 解析m3u8,获取其中的ts列表,多线程下载所有ts文件。 全部下完之后,用ffmpeg合…...

最后一击
第二届上海市青少年算法竞赛(小学组) 题目描述 Description 小爱和小艾两人组队打一只怪兽。一开始怪兽有 n 点生命值,当 n 变成 0 或更低时,怪兽就被消灭了。他们两人是同时开始攻击的,小爱每分钟可以攻击 a 下&…...

K8S资源管理方式
K8S资源管理方式 文章目录 K8S资源管理方式一、陈述式资源管理1.基础命令操作2.创建pod3.查看资源状态4.查看pod中的容器日志5.进入pod中的容器6.删除pod资源7.pod扩容8.项目生命周期管理(创建-->发布-->更新-->回滚-->删除)8.1创建services…...
第三章 图论 No.9有向图的强连通与半连通分量
文章目录 定义Tarjan求SCC1174. 受欢迎的牛367. 学校网络1175. 最大半连通子图368. 银河 定义 连通分量是无向图的概念,yxc说错了,不要被误导 强连通分量:在一个有向图中,对于分量中的任意两点u,v,一定能从…...

回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测
回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测 目录 回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测预测效果基本介绍模型描述程序设计参考…...

Mysql 和Oracle的区别
、mysql与oracle都是关系型数据库,Oracle是大型数据库,而MySQL是中小型数据库。但是MySQL是开源的,但是Oracle是收费的,而且比较贵。 1 2 mysql默认端口:3306,默认用户:root oracle默认端口&…...

在收藏夹里“积灰”的好东西——“收藏从未停止,行动从未开始”
方向一:分享一道你收藏的好题 小雅兰刚学数据结构与算法的时候,学的真的是很吃力,感觉链表真的特别的难,在学习了后面的知识之后,发现链表慢慢变得简单了,若是放在现在,小雅兰仍然觉得链表的知…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
