当前位置： 首页 > news >正文

分类过程中的一种遮挡现象

news 2025/9/26 19:58:53

( A, B )---3*30*2---( 1, 0 )( 0, 1 )

让网络的输入只有3个节点，AB训练集各由6张二值化的图片组成，让A，B中各有3个点，且不重合，统计迭代次数并排序。

其中有10组数据

差值结构

迭代次数

构造平均列A

构造平均列AB

平均列A

EA

平均列AB

EAB

EA+EAB

2

2

2

53740.37

2

2

2

-3

0

1.5

1.5

-3

-6

-6

-4.5

-

1

1

53740.37

-

1

1

-

1

1

3

1.5

2

-6

-4.5

-

-

-

53740.37

-

-

-

-

-

-

0

1.5

0

-6

-4.5

-

-

-

53740.37

-

-

-

-

-

-

0

1.5

0

-6

-4.5

-

-

-

53740.37

-

-

-

-

-

-

0

1.5

0

-6

-4.5

-

1

-

53740.37

-

1

-

-

-

2

1.5

0

-6

-4.5

0

1.5

0

-6

-4.5

2

2

2

54020.53

2

2

2

0

2

2

-3

-3

-3

-1

-

-

-

54020.53

-

-

-

-

-

-

0

2

0

-3

-1

-

1

1

54020.53

-

1

1

-

1

1

3

2

2

-3

-1

-

-

-

54020.53

-

-

-

-

-

-

0

2

0

-3

-1

-

-

-

54020.53

-

-

-

-

-

-

0

2

0

-3

-1

-

-

1

54020.53

-

-

1

-

-

2

2

0

-3

-1

0

2

0

-3

-1

2

2

2

53802.23

2

2

2

0

2

2

-3

-6

-6

-4

1

1

-

53802.23

1

1

-

1

1

-

3

2

2

-6

-4

-

-

-

53802.23

-

-

-

-

-

-

0

2

0

-6

-4

-

-

-

53802.23

-

-

-

-

-

-

0

2

0

-6

-4

1

-

-

53802.23

1

-

-

-

-

2

2

0

-6

-4

-

-

-

53802.23

-

-

-

-

-

-

0

2

0

-6

-4

0

2

0

-6

-4

2

2

2

53911.96

2

2

2

0

3

3

-3

-6

-6

-3

1

-

1

53911.96

1

-

1

1

-

1

3

3

2

-6

-3

-

-

-

53911.96

-

-

-

-

-

-

0

3

0

-6

-3

1

-

-

53911.96

1

-

-

-

-

2

3

0

-6

-3

-

-

-

53911.96

-

-

-

-

-

-

0

3

0

-6

-3

-

-

-

53911.96

-

-

-

-

-

-

0

3

0

-6

-3

0

3

0

-6

-3

2

2

2

53972.02

2

2

2

0

6

6

-3

-6

-6

0

-

1

1

53972.02

-

1

1

-

1

1

3

6

2

-6

0

-

1

-

53972.02

-

1

-

-

-

2

6

0

-6

0

-

-

-

53972.02

-

-

-

-

-

-

0

6

0

-6

0

-

-

-

53972.02

-

-

-

-

-

-

0

6

0

-6

0

-

-

-

53972.02

-

-

-

-

-

-

0

6

0

-6

0

0

6

0

-6

0

2

2

2

53905.34

2

2

2

0

3

3

-3

-3

-3

0

-

-

-

53905.34

-

-

-

-

-

-

0

3

0

-3

0

1

-

1

53905.34

1

-

1

1

-

1

3

3

2

-3

0

-

-

-

53905.34

-

-

-

-

-

-

0

3

0

-3

0

1

-

-

53905.34

1

-

-

-

-

2

3

0

-3

0

-

-

-

53905.34

-

-

-

-

-

-

0

3

0

-3

0

0

3

0

-3

0

2

2

2

54350.9

2

2

2

0

6

6

-3

-3

-3

3

-

-

-

54350.9

-

-

-

-

-

-

0

6

0

-3

3

-

1

1

54350.9

-

1

1

-

1

1

3

6

2

-3

3

-

-

1

54350.9

-

-

1

-

-

2

6

0

-3

3

-

-

-

54350.9

-

-

-

-

-

-

0

6

0

-3

3

-

-

-

54350.9

-

-

-

-

-

-

0

6

0

-3

3

0

6

0

-3

3

2

2

2

54569.45

2

2

2

0

3

3

-3

-2

-2

1

-

-

-

54569.45

-

-

-

-

-

-

0

3

0

-2

1

-

-

-

54569.45

-

-

-

-

-

-

0

3

0

-2

1

1

1

-

54569.45

1

1

-

1

1

-

3

3

2

-2

1

-

-

-

54569.45

-

-

-

-

-

-

0

3

0

-2

1

-

1

-

54569.45

-

1

-

-

-

2

3

0

-2

1

0

3

0

-2

1

2

2

2

54609.06

2

2

2

0

6

6

-3

-2

-2

4

-

-

-

54609.06

-

-

-

-

-

-

0

6

0

-2

4

-

-

-

54609.06

-

-

-

-

-

-

0

6

0

-2

4

1

1

-

54609.06

1

1

-

1

1

-

3

6

2

-2

4

1

-

-

54609.06

1

-

-

-

-

2

6

0

-2

4

-

-

-

54609.06

-

-

-

-

-

-

0

6

0

-2

4

0

6

0

-2

4

2

2

2

55200.75

2

2

2

0

6

6

-3

-1.5

-1.5

4.5

-

-

-

55200.75

-

-

-

-

-

-

0

6

0

-1.5

4.5

-

-

-

55200.75

-

-

-

-

-

-

0

6

0

-1.5

4.5

-

-

-

55200.75

-

-

-

-

-

-

0

6

0

-1.5

4.5

1

1

-

55200.75

1

1

-

1

1

-

3

6

2

-1.5

4.5

-

1

-

55200.75

-

1

-

-

-

2

6

0

-1.5

4.5

0

6

0

-1.5

4.5

如果等位点A为1，B为0，记为1；A为0，B为1记为2；AB都是1记为“+”；AB都是0记为“-”。

假设训练集的数字和数字之间有排斥，网络收敛迭代次数与排斥能成正比。假设排斥能由3部分构成E=EA+EB+EAB。

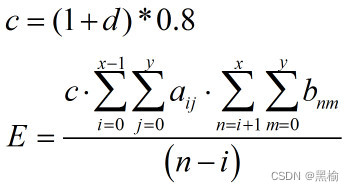
其中的EA和EB可以很简单的由上方法计算。但在计算AB之间的相互作用时假设这种作用只能在临近行之间进行，由于遮挡效应这种排斥无法隔行传递。

差值结构

迭代次数

构造平均列A

构造平均列AB

2

2

2

53740.37

2

2

2

-

1

1

53740.37

-

1

1

-

1

1

-

-

-

53740.37

-

-

-

-

-

-

-

-

-

53740.37

-

-

-

-

-

-

-

-

-

53740.37

-

-

-

-

-

-

-

1

-

53740.37

-

1

-

-

-

因为差值结构第5行的1被第2行的数字遮挡，因此第5行的1不参与两个训练集之间的排斥作用。因为B只有单行，因此排斥能为EB=0。因此总的排斥能就是EA+EAB。

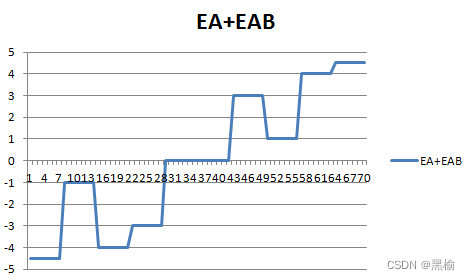
这条曲线和迭代次数成正比。

相关文章：

分类过程中的一种遮挡现象

( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 让网络的输入只有3个节点，AB训练集各由6张二值化的图片组成，让A，B中各有3个点，且不重合，统计迭代次数并排序。 其中有10组数据 差值结构 迭代次数 构造平均列A 构造平均列AB…...

编程日记 2023/8/14 13:09:05

下一代服务架构：单体架构--＞分布式架构--＞微服务(DDD)--＞软件定义架构(SDF with GraphEngine)

参考：自己实现一个SQL解析引擎_曾经的学渣的博客-CSDN博客...

编程日记 2023/8/14 13:08:03

excel 之 VBA

1、excel和VBA 高效办公，把重复性的工作写成VBA代码（VB代码的衍生物，语法和VBA相同）。 首先打开开发工具模式，如果没有选显卡，需要手动打开 打开程序编辑界面 快捷键 altF11一般操作 程序调试&#xf…...

编程日记 2023/8/14 13:07:02

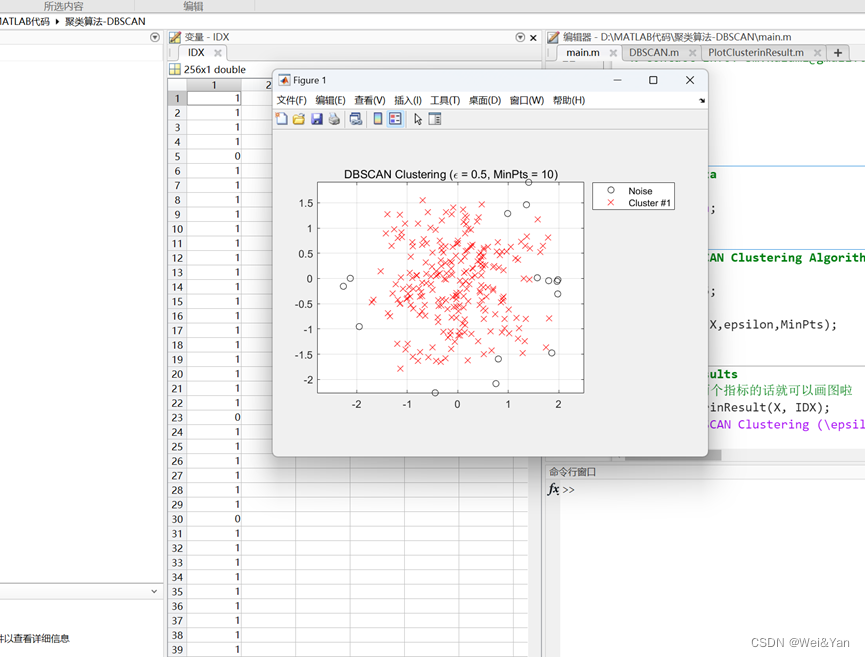
【数学建模】--聚类模型

聚类模型的定义： “物以类聚，人以群分”，所谓的聚类，就是将样本划分为由类似的对象组成的多个类的过程。聚类后，我们可以更加准确的在每个类中单独使用统计模型进行估计，分析或预测；也可以探究不…...

编程日记 2023/8/14 13:06:01

css3新增选择器总结

目录 一、属性选择器 二、结构伪类选择器 三、伪元素选择器 四、UI状态伪类选择器 五、反选伪类选择器 六、target选择器 七、父亲选择器、后代选择器 八、相邻兄弟选择器、兄弟们选择器 一、属性选择器 （除IE6外的大部分浏览器支持） E&#…...

编程日记 2023/8/14 13:04:59

0基础学C#笔记10：归并排序法

文章目录 前言一、递归的方式二、代码总结 前言 将一个大的无序数组有序，我们可以把大的数组分成两个，然后对这两个数组分别进行排序，之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的，所以在合并的时候是很…...

编程日记 2023/8/14 13:03:58

nlohmann json：通过for遍历object和array

object和array可以使用数for进行遍历： #include <iostream> #include <nlohmann/json.hpp> using namespace std; using json = nlohmann::json;auto checkJsonType(json& x) {if(x.type() == json::value_t::null){cout<<x<<" is null&quo…...

编程日记 2023/8/14 13:02:56

适配器模式：将不兼容的接口转换为可兼容的接口

适配器模式&#xff1a;将不兼容的接口转换为可兼容的接口 什么是适配器模式&#xff1f; 适配器模式是一种结构型设计模式&#xff0c;用于将一个类的接口转换为客户端所期望的另一个接口。它允许不兼容的类能够合作&#xff0c;使得原本由于接口不匹配而无法工作的类能够一…...

编程日记 2023/8/14 13:01:55

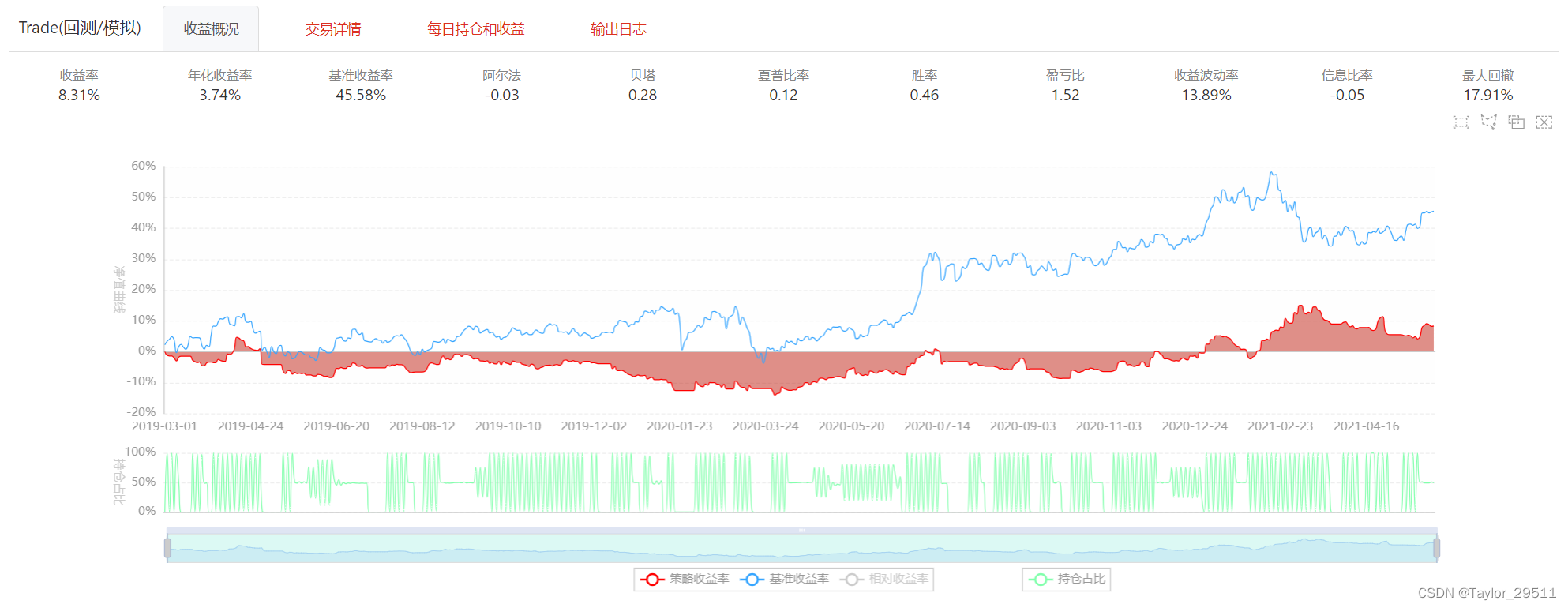
【量化课程】07_量化回测

文章目录 7.1 pandas计算策略评估指标数据准备净值曲线年化收益率波动率最大回撤Alpha系数和Beta系数夏普比率信息比率 7.2 聚宽平台量化回测实践平台介绍策略实现 7.3 Backtrader平台量化回测实践Backtrader简介Backtrader量化回测框架实践 7.4 BigQuant量化框架实战BigQuant简…...

编程日记 2023/8/14 13:00:53

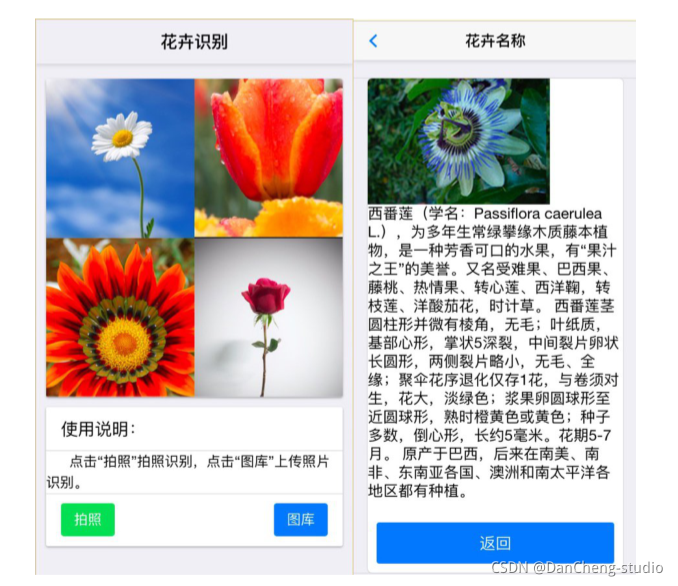
竞赛项目 深度学习花卉识别 - python 机器视觉 opencv

文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 &a…...

编程日记 2023/8/14 12:59:51

用对角线去遍历矩阵

声明 该系列文章仅仅展示个人的解题思路和分析过程&#xff0c;并非一定是优质题解&#xff0c;重要的是通过分析和解决问题能让我们逐渐熟练和成长&#xff0c;从新手到大佬离不开一个磨练的过程&#xff0c;加油&#xff01; 原题链接 用对角线遍历矩阵https://leetcode.c…...

编程日记 2023/8/14 12:58:51

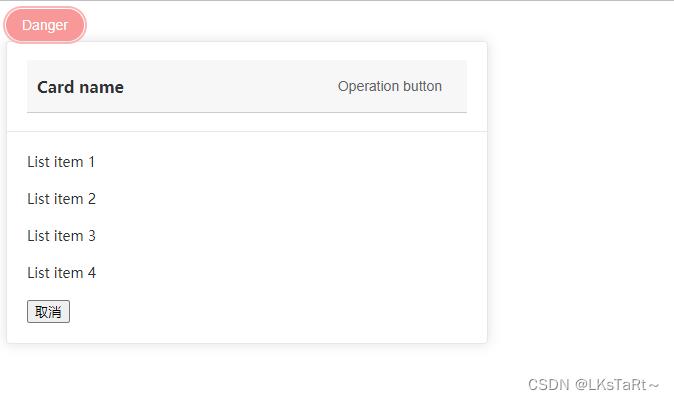
【vue】点击按钮弹出卡片，点击卡片中的取消按钮取消弹出的卡片（附代码）

实现思路&#xff1a; 在按钮上绑定一个点击事件&#xff0c;默认是true&#xff1b;在export default { }中注册变量给卡片标签用v-if判断是否要显示卡片&#xff0c;ture则显示&#xff1b;在卡片里面写好你想要展示的数据&#xff1b;给卡片添加一个取消按钮&#xff0c;绑…...

编程日记 2023/8/14 12:57:50

【K8S】pod 基础概念讲解

目录 Pod基础概念&#xff1a;在Kubrenetes集群中Pod有如下两种使用方式&#xff1a;pause容器使得Pod中的所有容器可以共享两种资源&#xff1a;网络和存储。总结&#xff1a;kubernetes中的pause容器主要为每个容器提供以下功能&#xff1a;Kubernetes设计这样的Pod概念和特殊…...

编程日记 2023/8/14 12:56:48

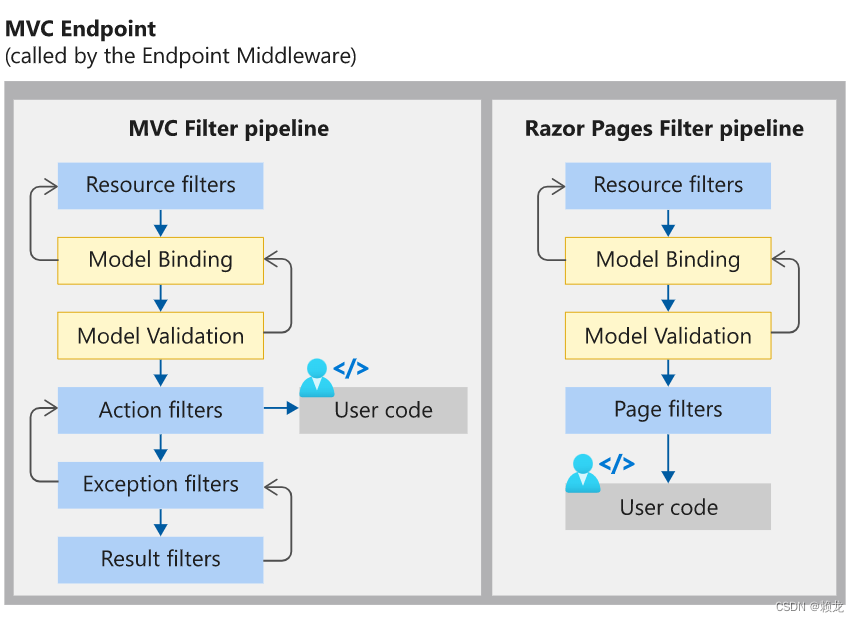
ASP.NET Core中间件记录管道图和内置中间件

管道记录 下图显示了 ASP.NET Core MVC 和 Razor Pages 应用程序的完整请求处理管道 中间件组件在文件中添加的顺序Program.cs定义了请求时调用中间件组件的顺序以及响应的相反顺序。该顺序对于安全性、性能和功能至关重要。 内置中间件记录 内置中间件原文翻译MiddlewareDe…...

编程日记 2023/8/14 12:55:40

[系统安全] 五十二.DataCon竞赛 (1)2020年Coremail钓鱼邮件识别及分类详解

您可能之前看到过我写的类似文章，为什么还要重复撰写呢？只是想更好地帮助初学者了解病毒逆向分析和系统安全，更加成体系且不破坏之前的系列。因此，我重新开设了这个专栏，准备系统整理和深入学习系统安全、逆向分析和恶意代码检测，“系统安全”系列文章会更加聚焦，更加系…...

编程日记 2023/8/14 12:54:38

Android学习之路(3) 布局

线性布局LinearLayout 前几个小节的例程中&#xff0c;XML文件用到了LinearLayout布局&#xff0c;它的学名为线性布局。顾名思义&#xff0c;线性布局 像是用一根线把它的内部视图串起来&#xff0c;故而内部视图之间的排列顺序是固定的&#xff0c;要么从左到右排列&#xf…...

编程日记 2023/8/14 12:53:36

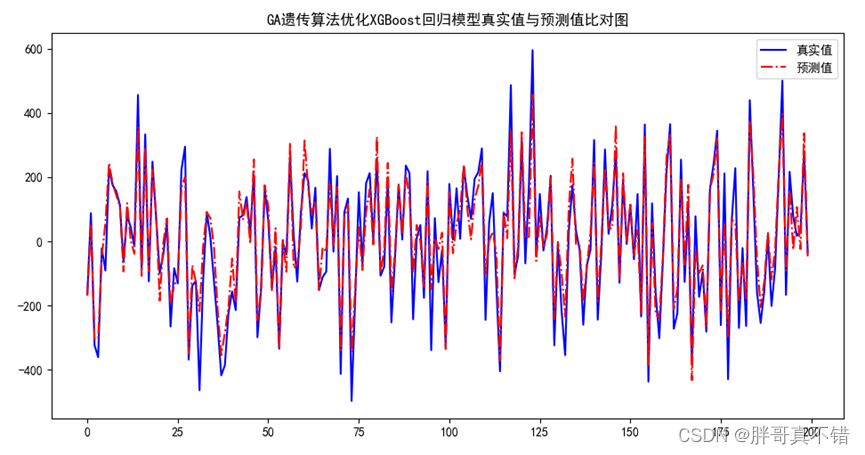
Python实现GA遗传算法优化XGBoost回归模型(XGBRegressor算法)项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 遗传算法&#xff08;Genetic Algorithm&#xff0c;GA&#xff09;最早是由美国的 John holland于20世…...

编程日记 2023/8/14 12:52:33

C#软件外包开发流程

C# 是一种由微软开发的多范式编程语言&#xff0c;常用于开发各种类型的应用程序&#xff0c;从桌面应用程序到移动应用程序和Web应用程序。下面和大家分享 C# 编程学习流程&#xff0c;希望对大家有所帮助。北京木奇移动技术有限公司&#xff0c;专业的软件外包开发公司&#…...

编程日记 2023/8/14 12:51:30

队列的实现

1.队列的概念 队列&#xff1a;只允许在一端进行插入数据操作&#xff0c;在另一端进行删除数据操作的特殊线性表&#xff0c;队列具有先进先出FIFO(First In First Out)。 入队列&#xff1a;进行插入操作的一端称为队尾 出队列&#xff1a;进行删除操作的一端称为队头 2.队列…...

编程日记 2023/8/14 12:50:29

Node + Express 后台开发 —— 起步

Node Express 后台开发 —— 起步 前面陆续学习了一下 node、npm、模块&#xff0c;也稍尝试 Express&#xff0c;感觉得换一个思路加快进行。 比如笔者对前端的开发已较熟悉&#xff0c;如果领导给一个内部小网站的需求&#xff0c;难道说你得给我配置一个后端&#xff1f;…...

编程日记 2023/8/14 12:49:28

设计模式和设计原则回顾

设计模式和设计原则回顾 23种设计模式是设计原则的完美体现，设计原则设计原则是设计模式的理论基石， 设计模式 在经典的设计模式分类中（如《设计模式：可复用面向对象软件的基础》一书中），总共有23种设计模式，分为三大类： 一、创建型模式（5种） 1. 单例模式（Sing…...

编程新知 2025/8/10 21:01:28

线程同步：确保多线程程序的安全与高效！

全文目录&#xff1a; 开篇语前序前言第一部分&#xff1a;线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分&#xff1a;synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分&#xff…...

编程新知 2025/9/24 16:02:40

MVC 数据库

MVC 数据库 引言 在软件开发领域，Model-View-Controller（MVC）是一种流行的软件架构模式，它将应用程序分为三个核心组件：模型（Model）、视图（View）和控制器（Controller）。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系，以…...

编程新知 2025/8/16 14:02:21

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2025/7/23 10:55:13

LLM基础1_语言模型如何处理文本

基于GitHub项目&#xff1a;https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken&#xff1a;OpenAI开发的专业"分词器" torch&#xff1a;Facebook开发的强力计算引擎&#xff0c;相当于超级计算器 理解词嵌入&#xff1a;给词语画"…...

编程新知 2025/9/25 5:16:24

JDK 17 新特性

#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持&#xff0c;不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的&#xff…...

编程新知 2025/8/17 10:25:39

.Net Framework 4/C# 关键字（非常用，持续更新...）

一、is 关键字 is 关键字用于检查对象是否于给定类型兼容，如果兼容将返回 true，如果不兼容则返回 false，在进行类型转换前，可以先使用 is 关键字判断对象是否与指定类型兼容，如果兼容才进行转换，这样的转换是安全的。 例如有：首先创建一个字符串对象，然后将字符串对象隐…...

编程新知 2025/9/25 18:41:38

Fabric V2.5 通用溯源系统——增加图片上传与下载功能

fabric-trace项目在发布一年后，部署量已突破1000次，为支持更多场景，现新增支持图片信息上链，本文对图片上传、下载功能代码进行梳理，包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源，需要对底层数据结构进行修改，在此对智能合约中的农产品数…...

编程新知 2025/8/9 23:42:13

Mysql中select查询语句的执行过程

目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析&#xff08;Parser&#xff09; 2.4、执行sql 1. 预处理&#xff08;Preprocessor&#xff09; 2. 查询优化器&#xff08;Optimizer&#xff09; 3. 执行器…...

编程新知 2025/9/24 6:17:05

R语言速释制剂QBD解决方案之三

本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

编程新知 2025/9/24 6:15:57