二叉搜索树K和KV结构模拟
一 什么是二叉搜索树
这个的结构特性非常重要,是后面函数实现的结构基础,二叉搜索树的特性是每个根节点都比自己的左树任一节点大,比自己的右树任一节点小。
例如这个图,

41是根节点,要比左树大,比右树小,满足但还不够,还要去看看41的左子树的根和右子树的根是否满足,更要判断这棵树上所有的根节点是不是都满足。而这棵树最厉害的地方之一我们用中序遍历(顺序左根右)便可以知道,遍历结果为13,15,17,22,28,33,37,41,42,50,53,58,61,66,78,排序不就排好了吗,复杂度可媲美快排和归并。二叉搜索树另一个功能那当然就是搜索了,例如我们要找66,66比根节点大,就不用去左子树找了,一下子少遍历一半,然后就去右子树找,和根节点58比较,66比58大,再去右子树找,再比较就找到了,最多查找高度次,满二叉树下为log(n)。而二叉搜索树是不是完美无缺,我也以为已经完美了,不好意思,我太年轻了,直到我看到下面这颗树。
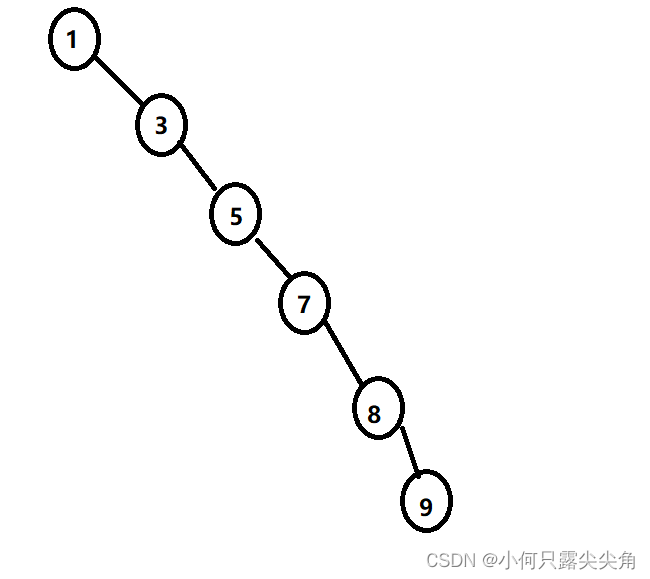
这个查找一次的效率就退化为O(N)了,解决办法:转化为平衡二叉树,通俗点就是换个根节点重新构造二叉树,例如把5或者7换成根节点,大家可以试试练习一下构建二叉树,构建完后的高度肯定比上图低,查找效率不就高了吗。
在说二叉搜索树的实现前,我们先说说什么是K结构,什么是KV结构,K结构就是只存一个数据,这个数据称为关键码,例如在英文词库里找一个英文单词,就是用关键码查找,需要的数据也是找到的关键码,但是KV结构就不同了,例如,通过拼音找汉字,这个时候拼音就是关键码,但是我们需要的数据不是拼音这个关键码,而是与之对应的汉字,这就是KV结构。
二 二叉搜索树K结构实现
1 树的节点类
template<class T>struct TreeNode{TreeNode(const T& val):_val(val)//_val可能为自定义类型,在初始化列表初始化方便调用构造函数{;}TreeNode* left = nullptr;TreeNode* right = nullptr;T _val;};2 BinaryTree树类
查找和排序都封装到了BinaryTree类中,和list一样,将节点类和树类分开封装。
(1) 默认构造函数
template<class T>class BinaryTree{public:typedef TreeNode<T> Node;BinaryTree(Node*node=nullptr) 该构造函数是用节点指针初始化,也可以再写个构造函数用个BinaryTree对象初始化:_root(node){;}private:Node* _root = nullptr;树类只需根节点地址即可管理整棵树};(2) 拷贝构造函数
因为两个copy函数都是用递归遍历二叉树,所以只能再写一个子函数,毕竟外部无法传_root指针。
void copy1(Node*tree)//前序遍历加复用insert拷贝二叉树{if (tree == nullptr)return;insert(tree->_val); 先插入根节点的值,再去左子树和右子树获取节点的数值insert内部会开辟空间copy(tree->left);copy(tree->right);}方法二比较巧妙的是它的第一个参数,root是外部传参_root的引用所以root=new node(),可以直接修改根节点而要拷贝左子树就传root->left的引用,这样new出来的节点可以直接连接到根的_left指针上。右子树同理。void copy2(Node*&root,Node*tree){if (tree== nullptr)return;root = new Node(tree->_val);copy2(root->left,tree->left);copy2(root->right,tree->right);}BinaryTree(const BinaryTree<T>&tree){//copy(tree._root);copy2(_root, tree._root);}copy2函数传指针引用我是受下面一个成员函数实现的启发,这个传引用一定要好好体会,方便理解后面的函数,非常巧妙。
(3) 赋值
用的是现代写法,比如t1,t2是两个BinaryTree对象,t1=t2就会调用下面的赋值函数,可是我的参数不是引用,那按规定自定义类型传值传参要用拷贝构造(我在类的成员函数博客曾提及),t2传参给tree就要调用拷贝构造,那tree就是一个新拷贝的对象,我们就可以用swap直接交换tree和t1的根节点指针,并且tree就是一个局部对象,函数调用完后会自动调用析构函数,省去了我们写析构t1树和创建新树的功夫,都给编译器做了。(string模拟的赋值也用到了现代写法)
void swap(BinaryTree<T>& tree){std::swap(_root, tree._root);}void operator=(BinaryTree<T> tree){swap(tree);}(4) find函数
搜索树怎么能缺少搜索功能呢
这个是find函数的子函数,子函数原因和上面同理,都是一开始传参外部无法获取_root,因为递归遍历代码量少,所以我实现的是递归版本bool _findR(Node*root,const T& val){if (root == nullptr)return false;if (val > root->_val)//val比当前_val大,去右树找{return _findR(root->right, val);}else if (val < root->_val)//val比当前_val小,去左树找{return _findR(root->left, val);}else {return true;//val和当前_val相等,返回true}}//下面这个是外部调用的find函数,只需要传要查找的值即可 bool find(const T& val){return _findR(_root, val);}
我之前在写find函数时,我还想着返回false是不是应该当左树和右树都没找到才返回false,好一会才醒悟,我们之所以去左树找,就是因为要找的val比根节点的值小,那右树更不会有了,所以左树找到nullptr就应该返回false,同理右树找到nullptr也返回false。
(5) insert函数
因为要递归去找合适的位置插入,所以同样要写一个子函数 void _insertR(Node*& root, const T&val){if (root == nullptr)当找到空节点,就可以插入了,此时才是引用起作用的时候{root = new Node(val); 直接就可以修改了,因为root是上一个节点的left或者 right指针的引用。return;}Node* cur = root;if (val > cur->_val)//val大于当前根,插入到右树去{_insertR(cur->right,val);}else if (val < cur->_val)//val小于当前根,插入到左树去{_insertR(cur->left, val);}else{return;}}void insert(const T& val){_insertR(_root, val);}(6) 中序遍历
void _Inorder(Node* root)//中序递归遍历{if (root == nullptr)return;_Inorder(root->left); 一直往左子树递归,直到左子树为空,算访问完,可以访问根。cout << root->_val << " "; _Inorder(root->right); 然后去右子树访问,同样分为左子树,根,右子树}void Inorder(){_Inorder(_root);//调用子函数,外部无法获取私有成员_root}(7) erase函数
bool _Rerase(Node*&root,const T&val){if (root == nullptr)return false;Node* cur = root;if (val > root->_val)//用_val找节点{return _Rerase(root->right, val);}else if (val < root->_val){return _Rerase(root->left, val);}else//找到了{//该节点只有一个或者无子节点if (root->left == nullptr) 由于root是上一节点左指针或者右指针的别名,所以可以直接拿root->right来赋值给root,否则还要 判断root->right是链接在上一节点的left指针还是 right指针。{root = root->right;}else if (root->right == nullptr){root = root->left;}else{删除有两个子节点的节点-替换法找该节点左子树中最大的,或者右子树中最小的来替换删除节点Node* leftMax = root->left;while (leftMax->right){leftMax = leftMax->right;}std::swap(leftMax->_val, root->_val);return _Rerase(root->left, val);调用_Rerase去删除leftMax节点,这里必须要传root->left,去左子树删除值为val的节点,不能传root例如我们交换leftMax的7和root的8值,如果传root,8的值比7大,就会去右树删,就找不到leftMax节点了,但是root的左子树仍然满足二叉搜索的特性,就可以找到leftMax节点并删除。 }delete cur; 该处统一释放删除节点,并返回truereturn true;}}bool erase(const T& val)//删除某个节点{return _Rerase(_root, val);}三 kv结构实现
本来我以为kv结构是要将K结构的树大改,当我实现后才发现,赋值可以直接照搬,,find,insert,erase中大量的if判断都是用关键码判断,根本不需要改动,中序遍历也就多打印一个数据,还有insert和拷贝构造函数要在new一个节点的时候多传一个参数。
接下来就看看一些比较重要的改动,在这里_key存关键码,而我上面二叉树K结构中是_val存的关键码,不要搞混了。
1 树的节点类
template<class T,class K>struct TreeNode{TreeNode(const T& val,const K&key):_val(val),_key(key){;} 类内可不加模板参数,也就是说TreeNode等价于TreeNode<T,k>TreeNode* left = nullptr; TreeNode* right = nullptr;T _val;//存与关键码对应的数据K _key;//_key存关键码};2 BinaryTree类
有了先前K结构树的基础,这里构造和析构函数我们就很好理解。
(1)构造和析构函数
template<class T, class K>class BinaryTree{public:typedef TreeNode<T,K> Node;BinaryTree(Node* node = nullptr) 默认构造无改变:_root(node){;}void _DestroyR(Node*&root) 递归释放节点,采用后序遍历的方式delete{if (root == nullptr)return;_DestroyR(root->left);_DestroyR(root->right);delete root;root = nullptr;}~BinaryTree(){_DestroyR(_root);}private:Node* _root = nullptr; 成员变量是不变的,毕竟kv结构的树用根节点同样可以管理};
}(3)erase函数
bool _Rerase(Node*& root, const T& key){if (root == nullptr)return false;Node* cur = root; //记录节点,方便后面deleteif (key > root->_key){return _Rerase(root->right,key);}else if (key <root->_key){return _Rerase(root->left, key);}else//找到了{//该节点只有一个或者无子节点if (root->left == nullptr){root = root->right;}else if (root->right == nullptr){root = root->left;}else{Node* leftMax = root->left;while (leftMax->right){leftMax = leftMax->right;}std::swap(leftMax->_val, root->_val); 在交换时要多交换一个值std::swap(leftMax->_key, root->_key);return _Rerase(root->left, key); 并且还是用key值去找leftMax删} 删除完leftMax后就直接return了,就不会重复删除。delete cur;return true;}}bool erase(const T& val)//删除某个节点{return _Rerase(_root, val);}二叉搜索树中最复杂的就是erase函数,大家在此处一定要画图理解。
相关文章:

二叉搜索树K和KV结构模拟
一 什么是二叉搜索树 这个的结构特性非常重要,是后面函数实现的结构基础,二叉搜索树的特性是每个根节点都比自己的左树任一节点大,比自己的右树任一节点小。 例如这个图, 41是根节点,要比左树大,比右树小&…...

nlohmann json:检查object是否存在某个键
1.通过find进行检查 #include <iostream> #include <nlohmann/json.hpp> using namespace std; using json = nlohmann::json;int main() {json data = R"({"name": "xiaoming","age": 10, "parent": [{"fat…...
15-1_Qt 5.9 C++开发指南_Qt多媒体模块概述
多媒体功能指的主要是计算机的音频和视频的输入、输出、显示和播放等功能,Qt 的多媒体模块为音频和视频播放、录音、摄像头拍照和录像等提供支持,甚至还提供数字收音机的支持。本章将介绍 Qt 多媒体模块的功能和使用。 文章目录 1. Qt 多媒体模块概述2. …...

分页查询中起始位置的计算
在分页查询中,page 和 pageSize 其实就是表示页数和每页的条数。这两个参数通常用于在数据库查询时进行分页。 如果你想根据 page 和 pageSize 计算数据的起始位置(例如,MySQL数据库的LIMIT查询),可以使用以下公式&am…...

Failed to execute goal org.apache.maven.plugins
原因: 这个文件D:\java\maven\com\ruoyi\pg-student\maven-metadata-local.xml出了问题 解决: 最简单的直接删除D:\java\maven\com\ruoyi\pg-student\maven-metadata-local.xml重新打包 或者把D:\java\maven\com\ruoyi\pg-student这个目录下所有文件…...

50吨收费站生活一体化污水处理设备厂家价格低
50吨收费站生活一体化污水处理设备厂家价格低 设备工艺说明 污水处理设备主要用于生活污水和与之类似的工业有机废水的处理,其主要处理方法是采用目前较为成熟的生化处理技术—生物接触氧化,水质设计按一般生活污水水质设计计算,按BOD5平均20…...
UG NX二次开发(C#)-CAM-获取刀具类型
文章目录 1、前言2、UG NX中的刀具类型3、获取刀具类型3.1 刀具类型帮助文档1、前言 在UG NX的加工模块,加工刀具是一个必要的因素,其包括了多种类型的类型,有铣刀、钻刀、车刀、磨刀、成型刀等等,而且每种刀具所包含的信息也各不相同。想获取刀具的信息,那就要知道刀具的…...
Flask 框架集成Bootstrap
前面学习了 Flask 框架的基本用法,以及模板引擎 Jinja2,按理说可以开始自己的 Web 之旅了,不过在启程之前,还有个重要的武器需要了解一下,就是著名的 Bootstrap 框架和 Flask 的结合,这将大大提高开发 Web …...

在k8s 1.26.6上部署ES集群
一、k8s集群架构: IP 角色,左边是ip,右边是hostname master1 是192.168.1.3 的hostname 192.168.1.3 master1 192.168.1.4 master2 192.168.1.5 master3 192.168.1.6 node1 192.168.1.7 node2 二、部署ES集群 1、配置stor…...

用神经网络玩转数据聚类:自编码器的原理与实践
目录 引言一、什么是自编码器二、自编码器的应用场景三、自编码器的优缺点四、如何实现基于自编码器的聚类算法五、总结 引言 随着数据量的爆炸性增长,如何有效地处理和分析数据成为了一个重要的问题。数据聚类是一种常用的数据分析方法,它可以将数据集…...

Linux系统调试课:Linux Kernel Printk
🚀返回专栏总目录 文章目录 0、printk 说明1、printk 日志等级设置2、屏蔽等级日志控制机制3、printk打印常用方式4、printk打印格式0、printk 说明 在开发Linux device Driver或者跟踪调试内核行为的时候经常要通过Log API来trace整个过程,Kernel API printk()是整个Kern…...
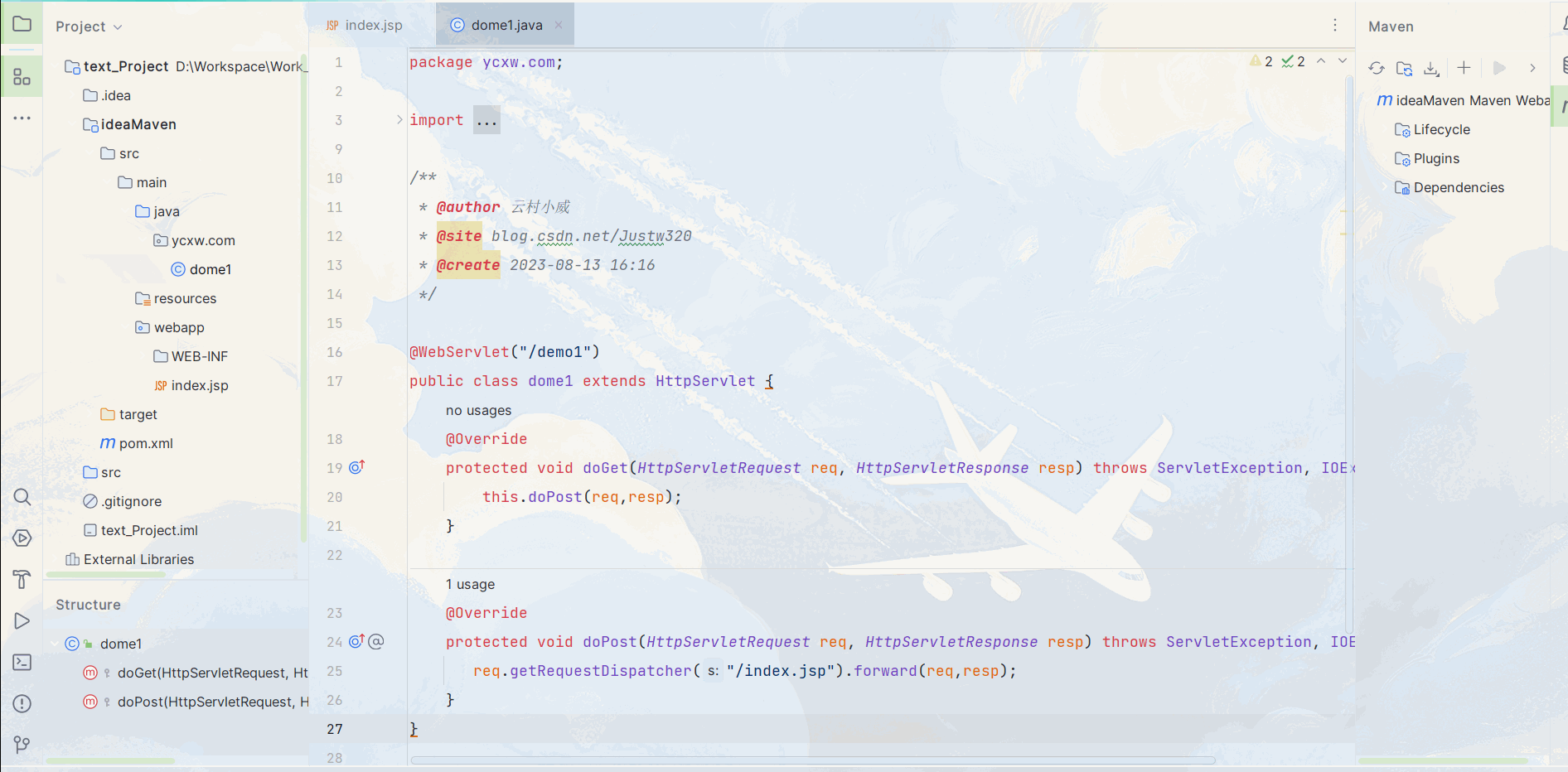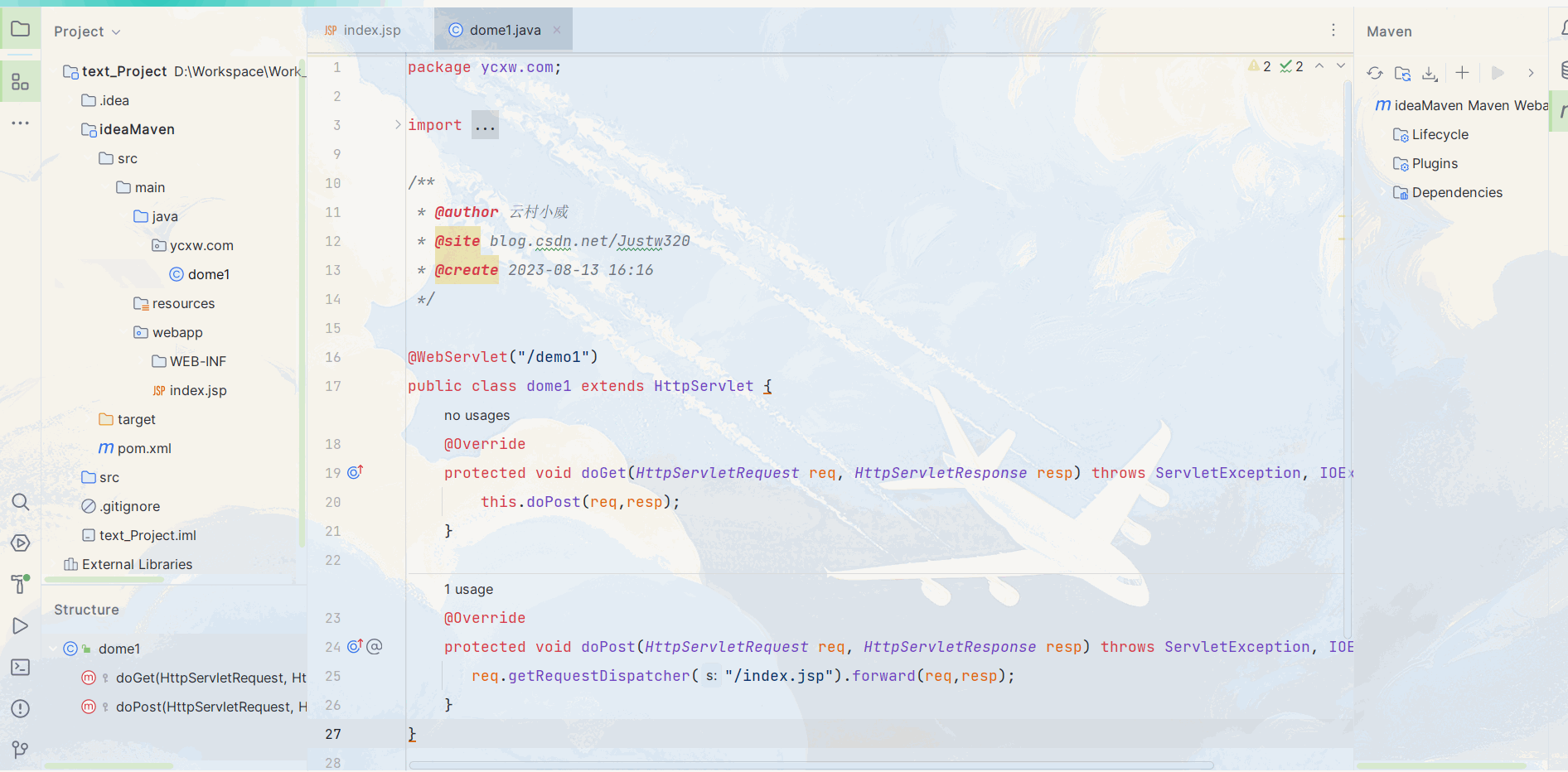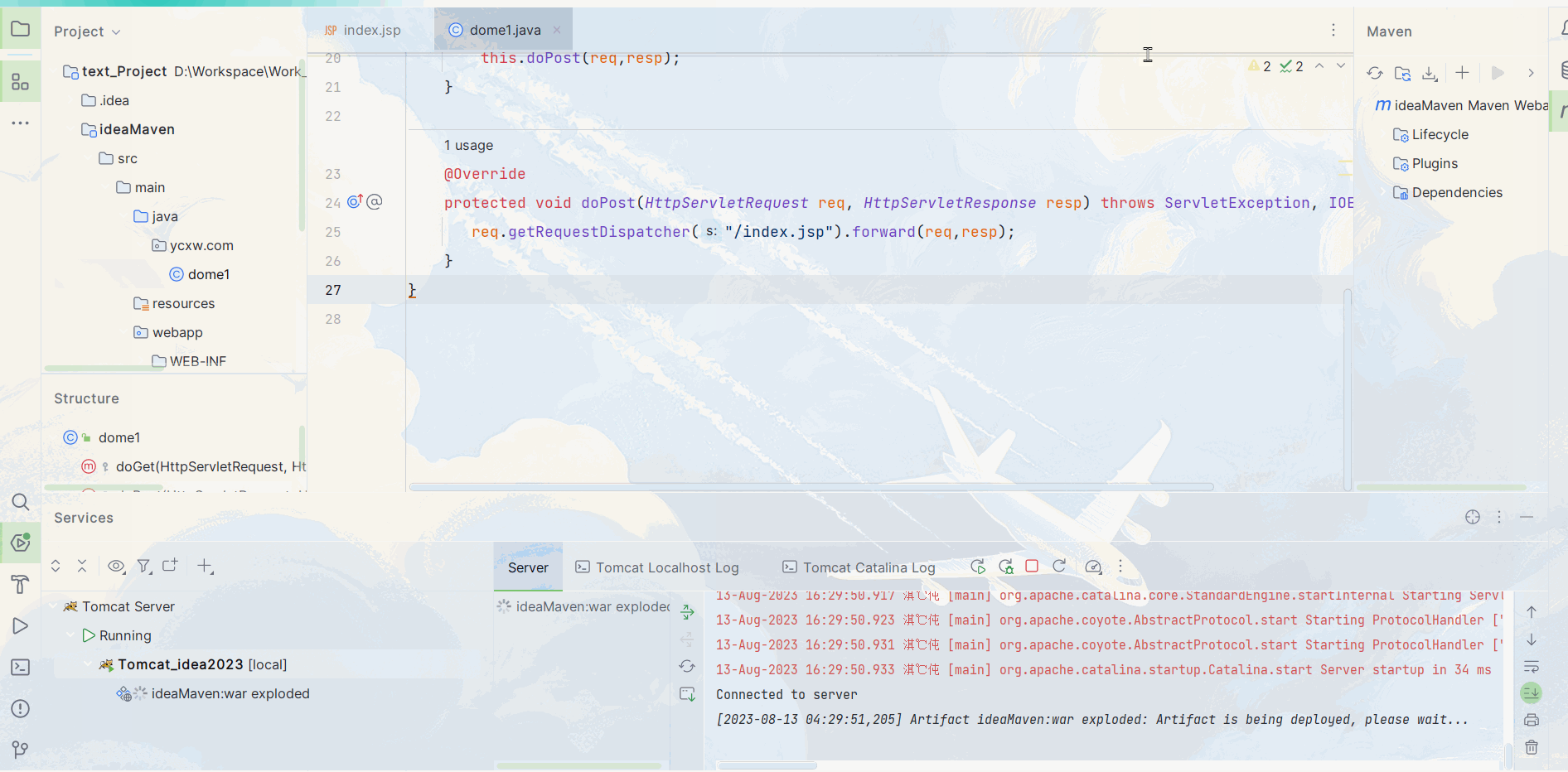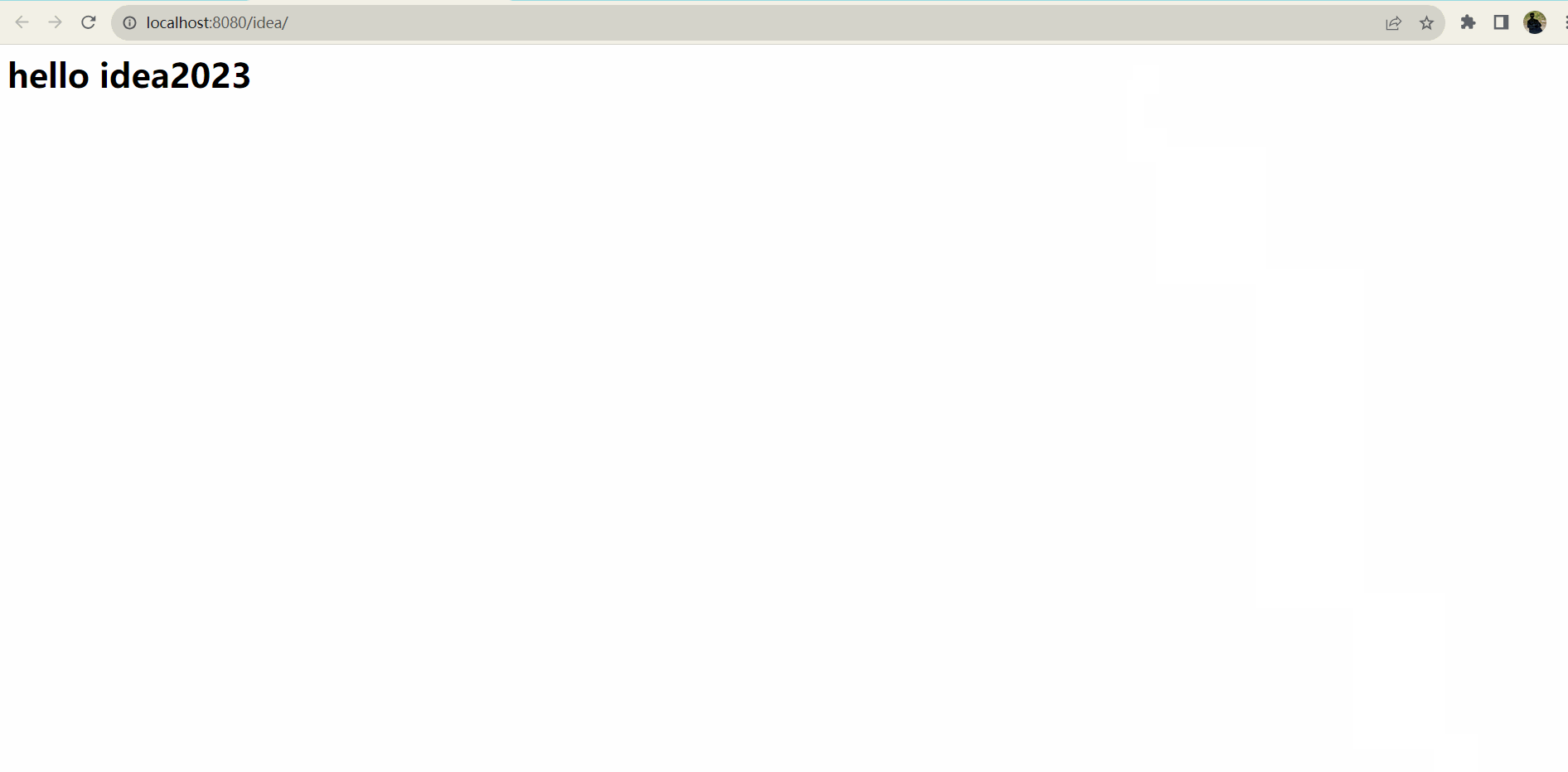
不同版本Idea部署Maven和Tomcat教学
目录 一、2019版Idea 1.1. Maven配置 1.2. Tomcat配置 二、2023版Idea 2.1 Maven配置 2.2. Tomcat配置 一、2019版Idea 1.1. Maven配置 在这篇 http://t.csdn.cn/oetKq 我已经详细讲述了Maven的下载安装及配置,本篇就直接开始实操 : 1. 首先进入设置搜索Mave…...

Vue 3.0中的Treeshaking?
1.treeshaking是什么? Tree shaking 是一种通过清除多余代码方式来优化项目打包体积的技术,专业术语叫 Dead code elimination 简单来讲,就是在保持代码运行结果不变的前提下,去除无用的代码 如果把代码打包比作制作蛋糕&#…...
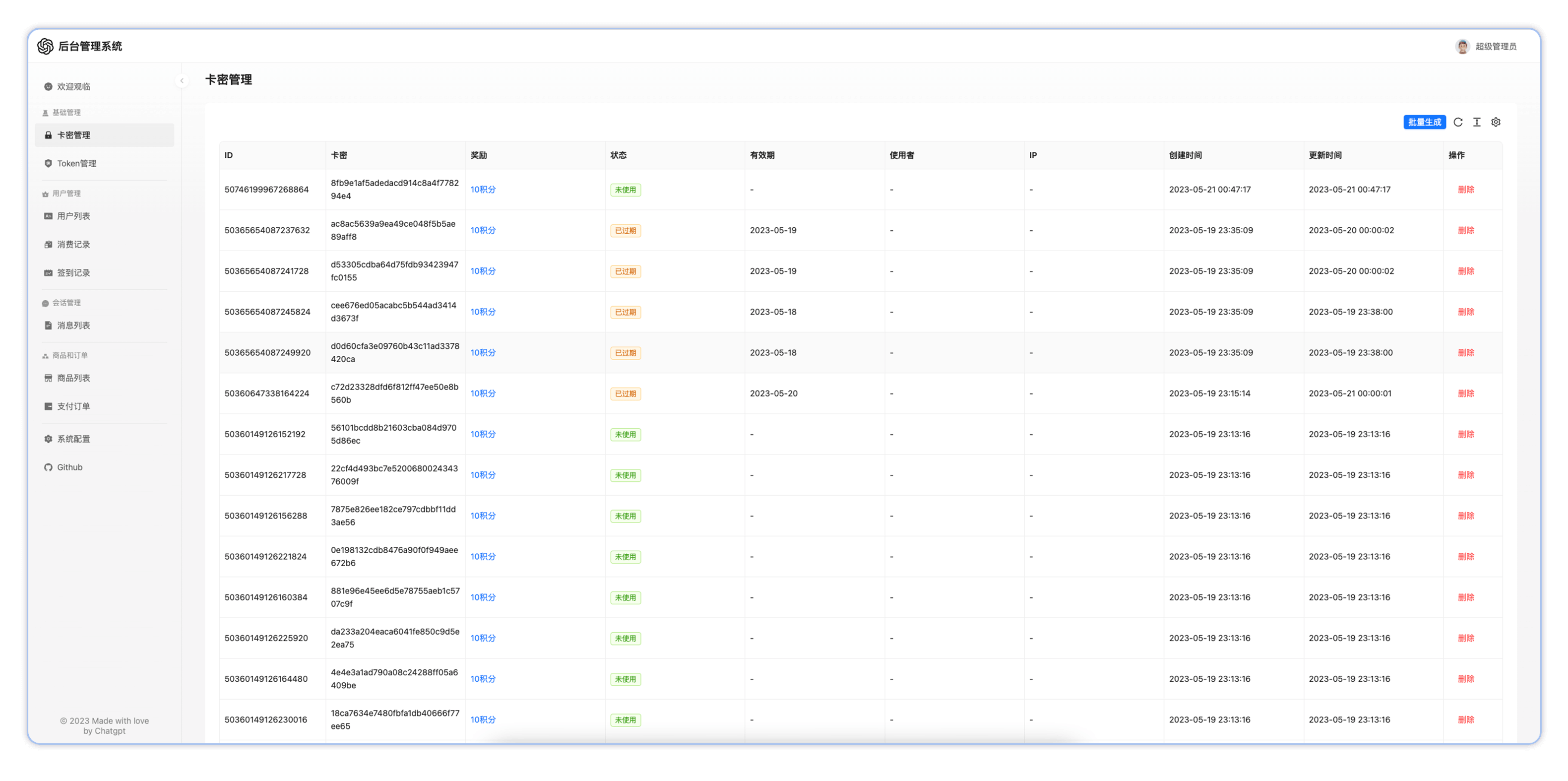
开源可商业运营的ChatGpt网页源码v1.2.2
🤖 主要功能 后台管理系统,可对用户,Token,商品,卡密等进行管理 精心设计的 UI,响应式设计 极快的首屏加载速度(~100kb) 支持Midjourney绘画和DALLE模型绘画,GPT4等应用 海量的内置 prompt 列表,来自中文和英文 一键导…...

驱动阿托斯DLHZO-T伺服比例阀放大器定制
DLHZO-T型伺服比例换向阀,直动式,带LVDT位置传感器和阀芯零遮盖,可应用于各种位置闭环控制实现最佳的性能。 比例阀和模块式数字放大器配合使用。 LVDT传感器和阀套结构可确保非常高的调节精度和响应灵敏度。 失电保护位可实现在电源中断的…...
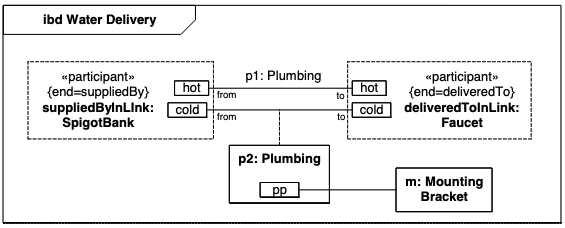
SysML V1.2 Blocks
本人看的实在是太枯燥了,很多都是机翻过了一遍 后面复习的时候,我再用chatgpt润色一下 一、综述 块是系统描述的模块化单元。每个块定义了一组特征来描述系统或其他感兴趣的元素。这些可能包括结构和行为特征,例如属性和操作,以…...

反编译微信小程序,可导出uniapp或taro项目
微信小程序反编译(全网通用) 微信小程序反编译 反编译主要分为四个阶段 操作流程 1. node.js安装 2. node安装模块 3. 开始反编译 4. 导入到微信开发者工具既可运行 微信小程序反编译 当碰到不会写的小程序功能时,正好看到隔壁小程序有类似…...
鉴源实验室丨汽车网络安全攻击实例解析(二)
作者 | 田铮 上海控安可信软件创新研究院项目经理 来源 | 鉴源实验室 社群 | 添加微信号“TICPShanghai”加入“上海控安51fusa安全社区” 引言:汽车信息安全事件频发使得汽车行业安全态势愈发紧张。这些汽车网络安全攻击事件,轻则给企业产品发布及产品…...
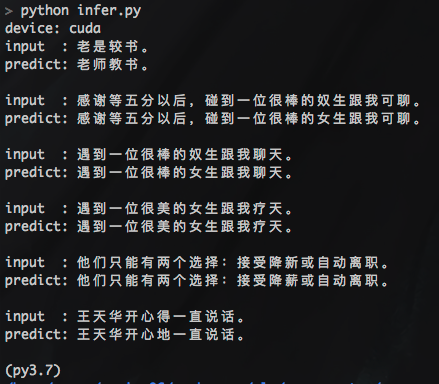
pycorrector一键式文本纠错工具,整合了BERT、MacBERT、ELECTRA、ERNIE等多种模型,让您立即享受纠错的便利和效果
pycorrector:一键式文本纠错工具,整合了Kenlm、ConvSeq2Seq、BERT、MacBERT、ELECTRA、ERNIE、Transformer、T5等多种模型,让您立即享受纠错的便利和效果 pycorrector: 中文文本纠错工具。支持中文音似、形似、语法错误纠正,pytho…...

Linux 日志管理
Linux 日志管理 一.Linux 下的日志服务简介 1.1 CentOS5 之前的版本 centos5 之前的版本使用系统和内核日志分离的格式记录日志 syslogd:该服务专门用于记录系统日志(system application logs) klogd: 该服务专门用于记录内核日志(linux kernel logs) centos5 之前事件的记录格…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
