企业有VR全景拍摄的需求吗?能带来哪些好处?
在传统图文和平面视频逐渐疲软的当下,企业商家如何做才能让远在千里之外的客户更深入、更直接的详细了解企业品牌和实力呢?千篇一律的纸质材料已经过时了,即使制作的再精美,大家也会审美疲劳;但是你让客户远隔千里,就能720°环游企业,这个效果就足以吸引很多客户的关注了。
企业拍摄制作VR全景,能够让客户在线实景了解企业、产品和文化,为企业和客户之间搭建沟通桥梁。VR全景拍摄可以为企业带来哪些好处?

1、VR全景拍摄为客户实现身临其境的沉浸式体验,让客户仿佛置身于实景中,相隔千里也能通过高清图像和逼真的音效,感受真实且震撼的视听体验。
真实、直观、丰富的展现方式,有助于提高客户对企业的认知和信任,促进客户粘度;还能为客户节约来回的时间成本和精力,客户的满意度自然也会提高。

2、VR全景拍摄提供更加立体的展示内容,720度真实临场感就是VR全景拍摄制作的优势,客户通过主动旋转全景视角,上下前后左右720°视角让客户无死角观察产品,把平面图片所触及不到的边界线以外的内容统统展现在浏览者面前。

三维模型所打造的商品打破了同质化展现方式,多维度、立体化还原物品各个角度,物品呈现高真实展示效果。令商品动起来,这种可视化视觉说明书更加受客户的青睐。

3、VR全景拍摄制作还能够实现交互性展示,比如动态交互、AI数字人等功能,从现阶段来看,加持了AI数字人的VR虚拟展厅更加受企业欢迎,不仅拥有专属IP属性的虚拟代言人,还能够进一步提高企业品牌形象、展现企业硬实力,这种交互式格局能够快速拉近用户和企业之间的距离。
有着外贸产业的企业,还可以通过VR全景的中英文切换功能,吸引国外客户前来投资,快速建立信任,加快合作环节。VR全景逐渐成为了商企不可或缺的营销工具,在展示品牌形象、吸引客户关注以及开拓市场等方面都有着强有力的作用,帮助商企在竞争激烈的市场中脱颖而出,所以说,企业很有必要做VR全景拍摄。
相关文章:

企业有VR全景拍摄的需求吗?能带来哪些好处?
在传统图文和平面视频逐渐疲软的当下,企业商家如何做才能让远在千里之外的客户更深入、更直接的详细了解企业品牌和实力呢?千篇一律的纸质材料已经过时了,即使制作的再精美,大家也会审美疲劳;但是你让客户远隔千里&…...

【问题解决】Git命令行常见error及其解决方法
以下是我一段时间没有使用xshell,然后用git命令行遇到的一些系列错误和他们的解决方法 遇到了这个报错: fatal: Not a git repository (or any of the parent directories): .git 我查阅一些博客和资料,可以解决的方式: git in…...

【100天精通python】Day34:使用python操作数据库_ORM(SQLAlchemy)使用
目录 专栏导读 1 ORM 概述 2 SQLAlchemy 概述 3 ORM:SQLAlchemy使用 3.1 安装SQLAlchemy: 3.2 定义数据库模型类: 3.3 创建数据表: 3.4 插入数据: 3.5 查询数据: 3.6 更新数据: 3.7 删…...
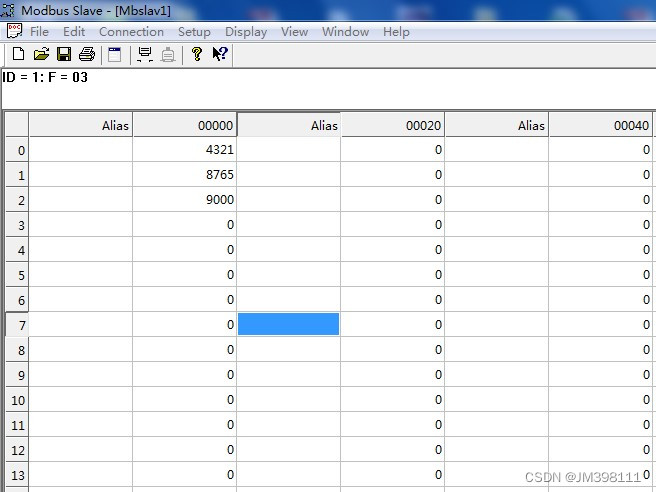
CCLINK IE转MODBUS-TCP网关modbus tcp协议详解
你是否曾经遇到过需要同时处理CCLINK IE FIELD BASIC和MODBUS两种数据协议的情况?捷米的JM-CCLKIE-TCP网关可以帮助你解决这个问题。 捷米JM-CCLKIE-TCP网关可以分别从CCLINK IE FIELD BASIC一侧和MODBUS一侧读写数据,然后将数据存入各自的缓冲区。接着…...

vue2根据不同的电脑分辨率显示页面内容及不同设备适配显示
1.安装插件: npm install postcss-px2rem px2rem-loader --save npm i lib-flexible --save 2.创建flexible.js,并在main.js引用 ;(function(win, lib) {var doc = win.document;var docEl = doc.documentElement;var metaEl = doc.querySelector(meta[name="viewport&…...

概率论:多维随机变量及分布
多维随机变量及分布 X X X为随机变量, ∀ x ∈ R , P { X ≤ x } F ( x ) \forall x\in R,P\{X\le x\}F(x) ∀x∈R,P{X≤x}F(x) 设 F ( x ) F(x) F(x)为 X X X的分布函数,则 (1) 0 ≤ F ( x ) ≤ 1 0\le F(x)\le1 0≤F(x)≤1 &am…...
flutter-第三方组件
卡片折叠 stacked_card_carousel 扫一扫组件 qr_code_scanner 权限处理组件 permission_handler 生成二维码组件 pretty_qr_code 角标组件 badges 动画组件 animations app更新 app_installer 带缓存的图片组件 cached_network_image 密码输入框 collection 图片保存 image_g…...
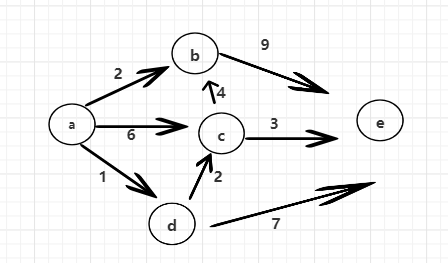
迪瑞克斯拉算法
迪锐克斯拉算法 简单来说就是在有向图中,给定一个图中具体的出发点,从这个点出发能够到达的所有的点,每个点的最短距离是多少。到不了的点,距离则是正无穷。有向,无负权重,可以有环。 所以说,迪…...
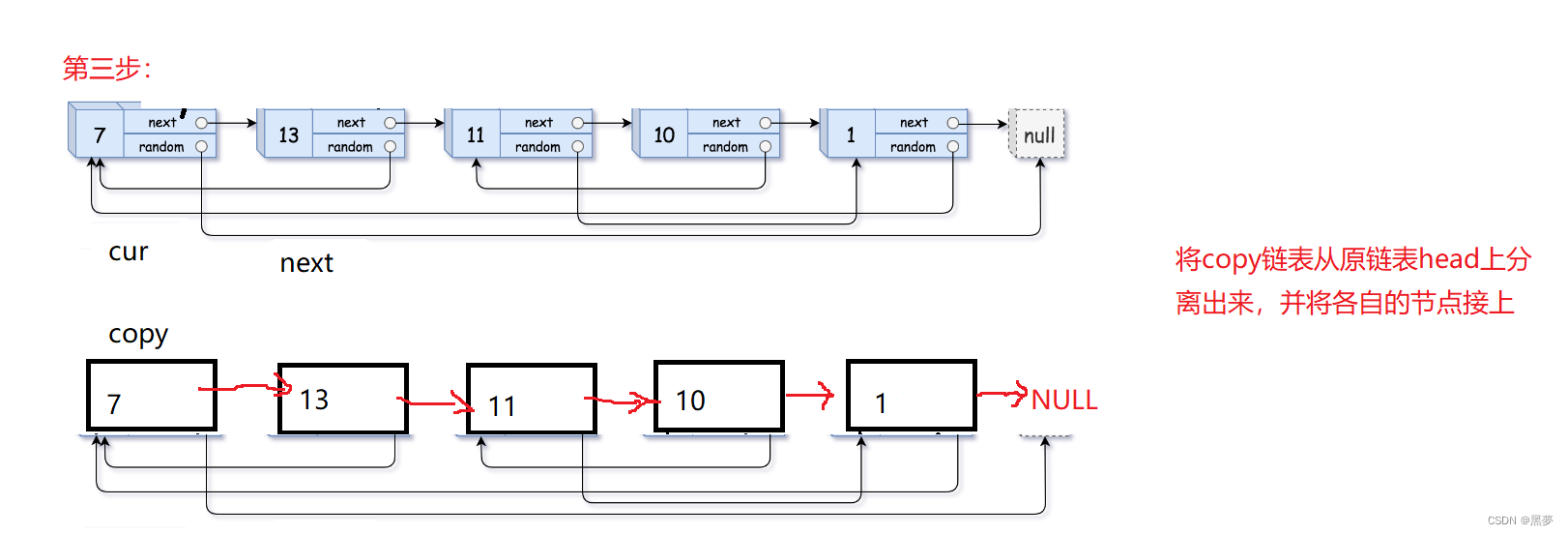
数据结构:力扣OJ题(每日一练)
目录 题一:环形链表 思路一: 题二:复制带随机指针的链表 思路一: 本人实力有限可能对一些地方解释的不够清晰,可以自己尝试读代码,望海涵! 题一:环形链表 给定一个链表的头节点…...

【论文阅读】基于深度学习的时序预测——Informer
系列文章链接 论文一:2020 Informer:长时序数据预测 论文二:2021 Autoformer:长序列数据预测 论文三:2022 FEDformer:长序列数据预测 论文四:2022 Non-Stationary Transformers:非平…...

机器学习 | Python实现GBDT梯度提升树模型设计
机器学习 | Python实现GBDT梯度提升树模型设计 目录 机器学习 | Python实现GBDT梯度提升树模型设计基本介绍模型描述模型使用参考资料基本介绍 机器学习 | Python实现GBDT梯度提升树模型设计。梯度提升树(Grandient Boosting)是提升树(Boosting Tree)的一种改进算法,GBDT也…...
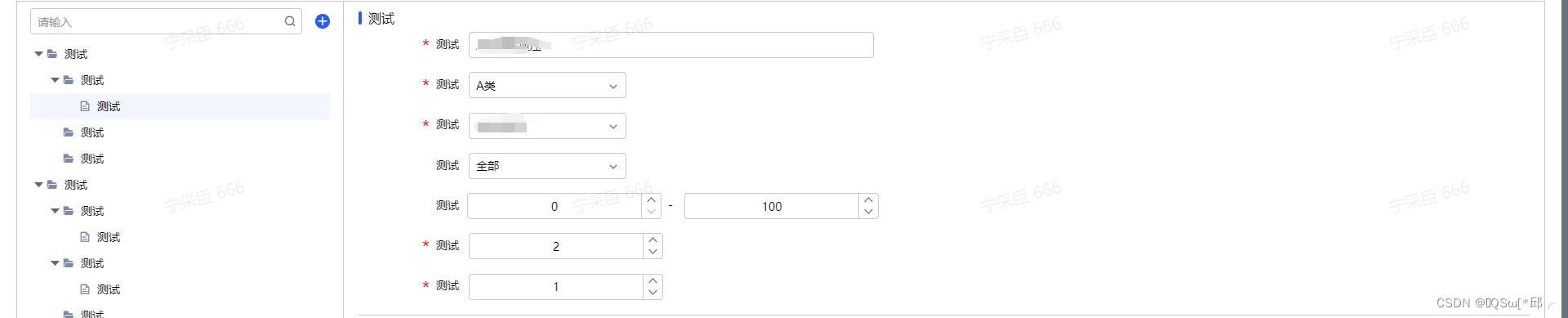
elementUi表单恢复至初始状态并不触发表单验证
elementUi表单恢复至初始状态并不触发表单验证 1.场景再现2.解决方法 1.场景再现 左侧是树形列表,右侧是显示节点的详情,点击按钮应该就是新增一个规则的意思,表单内容是没有改变的,所以就把需要把表单恢复至初始状态并不触发表单…...
大模型相关知识
一. embedding 简单来说,embedding就是用一个低维的向量表示一个物体,可以是一个词,或是一个商品,或是一个电影等等。这个embedding向量的性质是能使距离相近的向量对应的物体有相近的含义,比如 Embedding(复仇者联盟)…...

无法在 macOS Ventura 上启动 Multipass
异常信息 ➜ ~ sudo multipass authenticate Please enter passphrase: authenticate failed: Passphrase is not set. Please multipass set local.passphrase with a trusted client. ➜ ~ multipass set local.passphrase Please enter passphrase: Please re-enter…...

算法通关村第六关——原来如此简单
层次遍历:又叫广度优先遍历。就是从根节点开始,先访问根节点下面一层全部元素,再访问之后的层次,直到访问完二叉树的最后一层。 我们先看一下基础的层次遍历题,力扣102题:给你一个二叉树,请你返…...
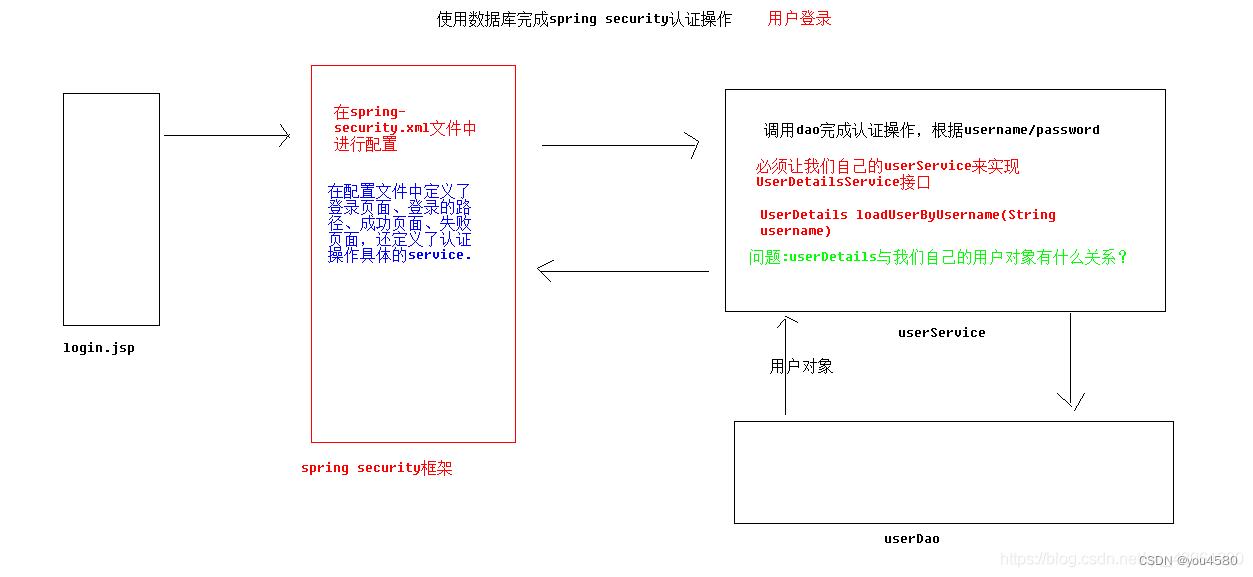
企业权限管理(八)-登陆使用数据库认证
Spring Security 使用数据库认证 在 Spring Security 中如果想要使用数据进行认证操作,有很多种操作方式,这里我们介绍使用 UserDetails 、 UserDetailsService来完成操作。 UserDetails public interface UserDetails extends Serializable { Collecti…...
第一百二十五天学习记录:C++提高:STL-deque容器(下)(黑马教学视频)
deque插入和删除 功能描述: 向deque容器中插入和删除数据 函数原型: 两端插入操作: push_back(elem); //在容器尾部添加一个数据 push_front(elem); //在容器头部插入一个数据 pop_back(); //删除容器最后一个数据 pop_front(); //删除容器…...

案例12 Spring MVC入门案例
网页输入http://localhost:8080/hello,浏览器展示“Hello Spring MVC”。 1. 创建项目 选择Maven快速构建web项目,项目名称为case12-springmvc01。 2.配置Maven依赖 <?xml version"1.0" encoding"UTF-8"?><project xm…...

【React】精选10题
1.React Hooks带来了什么便利? React Hooks是React16.8版本中引入的新特性,它带来了许多便利。 更简单的状态管理 使用useState Hook可以在函数组件中方便地管理状态,避免了使用类组件时需要继承React.Component的繁琐操作。 避免使用类组件…...

VS Spy++进程信息获取
查看进程中窗口信息。 Spy使用介绍 Windows下的程序及热键监视神器——Spy Word进程获取...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
