【动态规划基础】数字三角形(IOI1994)
题目描述
数字三角形

输入输出样例
输入样例#1:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5输出样例#1:
30
思路:
这题可能看到的第一眼——直接贪心然后一层一层判断呀!!!不过很快又会发现,额___好像不行。因为可能当前选的是一个大的,但是后面全都是小的!!!
所以这时我们就需要用到动态规划了
动态规划基础知识详见: 动态规划基础(超详细)
这题我们从上到下行不通,那我们就要思考从下到上进行操作
首先需要知道状态转移方程:
从图中可知当前这这个可以由左下角的数与右下角的数的最大值加上自己本来的数
所以状态转移方程为:
dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];
然后我们需要知道DP的初值,那这题很明显,就是输入的最后一行,也就是:
for(int i=1;i<=n;i++) dp[n][i]=a[n][i];
AC代码
最后呈上完整代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[101][101],dp[101][101];
int main(){cin>>n;for(int i=1;i<=n;i++)for(int j=1;j<=i;j++) cin>>a[i][j];for(int i=1;i<=n;i++) dp[n][i]=a[n][i];for(int i=n-1;i>=1;i--){for(int j=1;j<=i;j++){dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];}}cout<<dp[1][1];return 0;
}
相关文章:

【动态规划基础】数字三角形(IOI1994)
题目描述 数字三角形 输入输出样例 输入样例#1: 5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5输出样例#1: 30思路: 这题可能看到的第一眼——直接贪心然后一层一层判断呀!!!不过很快又会发现,额___好…...

yolo源码注释2——数据集配置文件
代码基于yolov5 v6.0 目录: yolo源码注释1——文件结构yolo源码注释2——数据集配置文件yolo源码注释3——模型配置文件yolo源码注释4——yolo-py 数据集配置文件一般放在 data 文件夹下的 XXX.yaml 文件中,格式如下: path: # 数据集存放路…...
)
Java实现根据姓名生成头像(钉钉样式)
头像生成器代码如下: package com.hua.util;import org.apache.commons.lang3.StringUtils;import javax.imageio.ImageIO; import java.awt.*; import java.awt.geom.RoundRectangle2D; import java.awt.image.BufferedImage; import java.io.File; import java.i…...

微信小程序备案流程
微信小程序备案流程 📔 千寻简笔记介绍 千寻简笔记已开源,Gitee与GitHub搜索chihiro-notes,包含笔记源文件.md,以及PDF版本方便阅读,且是用了精美主题,阅读体验更佳,如果文章对你有帮助请帮我…...
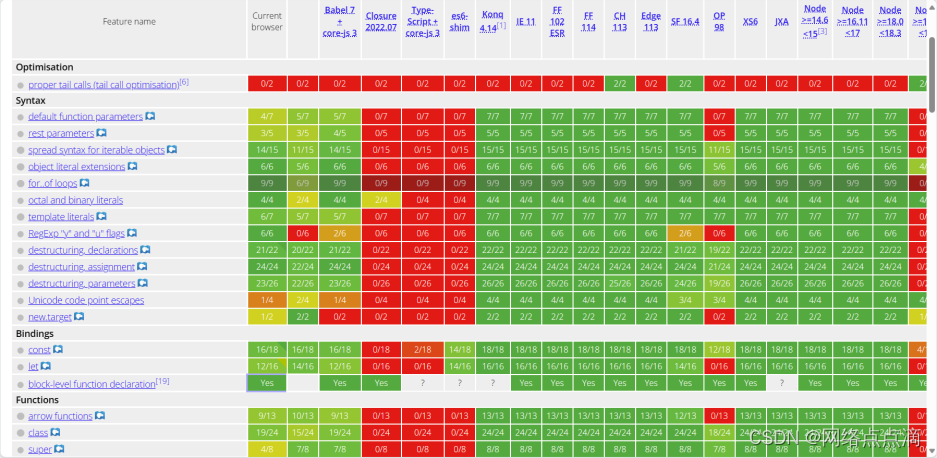
JavaScript版本ES5/ES6及后续版本
JavaScript简史 1995: Brendan Eich在短短10天内创建了JavaScript的第一个版本。它被称为摩卡,但已经具备了现代JavaScript的许多基本特性! 1996: 为了吸引Java开发人员,Mocha先是更改为LiveScript,然后又更改为Ja…...
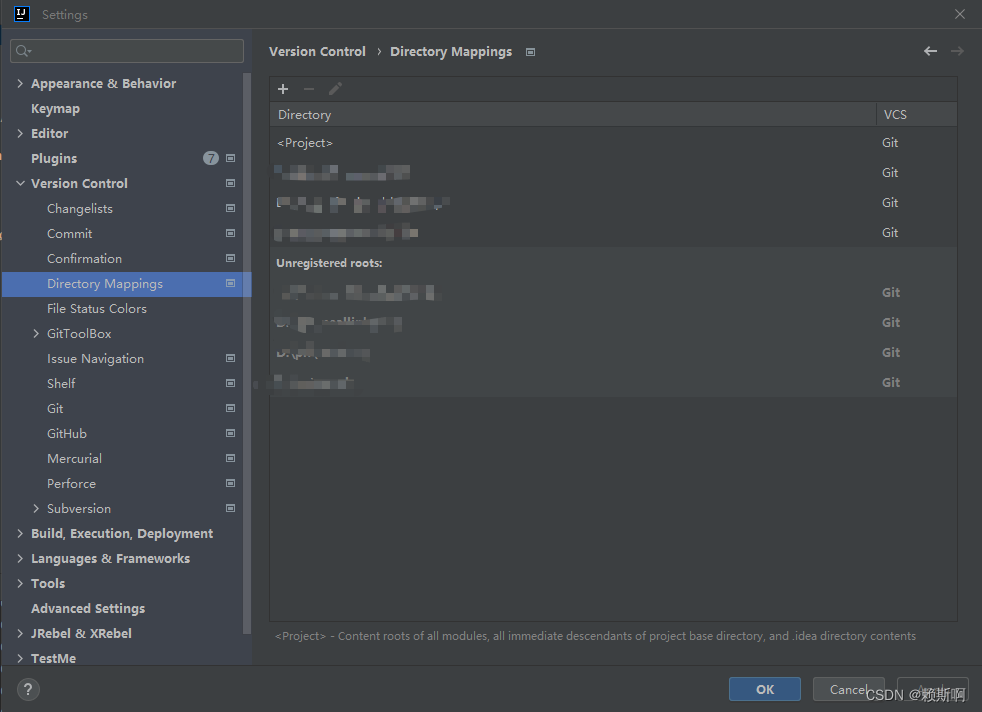
解决Idea 多模块,maven项目是多层级文件夹的子项时无法加入git管理的问题
问题 多模块项目,引入模块无法做git管理,第一个项目没有git分支标志,也不能像其他项目一样右键出git选项。 解决方法 发现该模块是多层级的文件夹结构,也就是项目本身在一个文件夹下。应该是要管理该文件夹。 Settings-Versi…...

yolo源码注释4——yolo-py
代码基于yolov5 v6.0 目录: yolo源码注释1——文件结构yolo源码注释2——数据集配置文件yolo源码注释3——模型配置文件yolo源码注释4——yolo-py yolo.py 用于搭建 yolov5 的网络模型,主要包含 3 部分: Detect:Detect 层Model…...

计算机网络中速率和带宽的区别
速率,指的是连接在计算机网络上的主机在数字信道上传送数据的速率,它也称为数据率或比特率,单位是bps。速率往往指的是额定速率或者标称速率,意思也就是在非常理想的情况下才能达到的数据传送的速率,然而在现实生活中是…...

MySQL数据库练习
目录 表结构 建表 插入数据 1、用SQL语句创建学生表student,定义主键,姓名不能重名,性别只能输入男或女,所在系的默认值是 “计算机”。 2、修改student 表中年龄(age)字段属性,数据类型由…...

Redis BitMap/HyperLogLog/GEO/布隆过滤器案例
面试问题: 抖音电商直播,主播介绍的商品有评论,1个商品对应了1系列的评论,排序展现取前10条记录用户在手机App上的签到打卡信息:1天对应1系列用户的签到记录,新浪微博、钉钉打卡签到,来没来如何…...
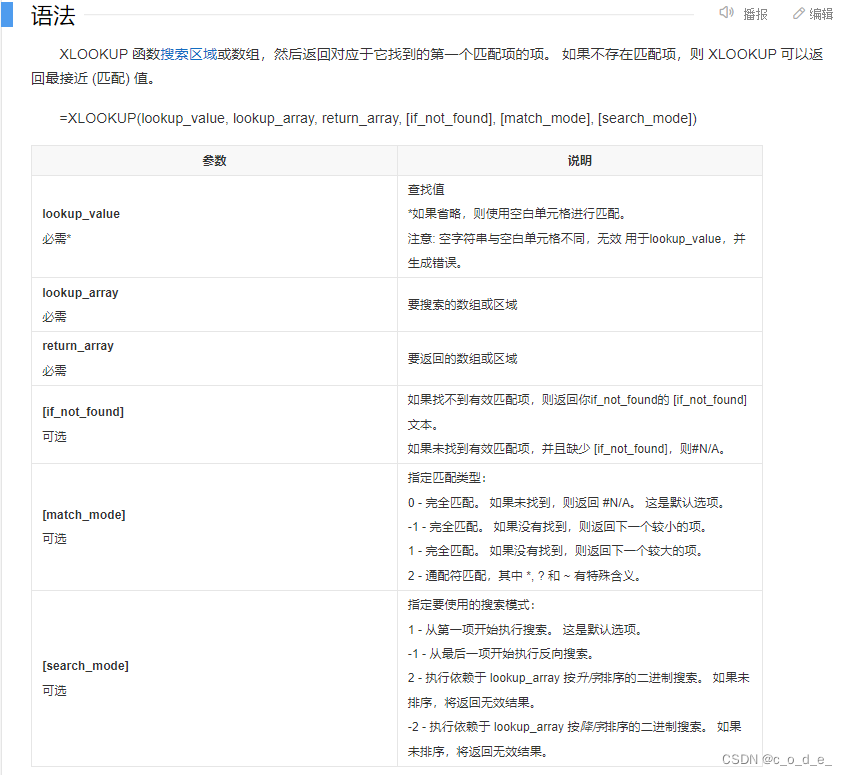
POI处理excel,根据XLOOKUP发现部分公式格式不支持问题
poi4不支持XLOOKUP函数,但poi最新的5.2.3却已经对此函数做了支持 poi下载地址:Index of /dist/poi/release/bin 公式源码位置:org/apache/poi/ss/formula/atp/XLookupFunction.java 但是在使用此函数过程中,发现有些XLOOKUP函数会…...

第一次PR经历
第一次PR测试地址:https://github.com/firstcontributions/first-contributions说明文档: https://github.com/firstcontributions/first-contributions/blob/main/translations/README.zh-cn.md...

背上小书包准备面试之TypeScript篇
目录 typescript是啥?与javascript的区别? typescript数据类型? typescript中枚举类型?应用场景? typescript中接口的理解?应用场景? typescript中泛型的理解?应用场景…...

【Spring】浅谈spring为什么推荐使用构造器注入
目录 一、前言 二、常见的三种注入方式 2.1 field注入 2.2 构造器注入 2.3 setter注入 三、构造器注入的好处 四、答疑 五、总结 一、前言 Spring框架对Java开发的重要性不言而喻,其核心特性就是IOC(Inversion of Control, 控制反转&…...

在阿里云Linux服务器上部署MySQL数据库流程
阿里云百科分享在阿里云Linux服务器上部署MySQL数据库流程,MySQL是一个关系型数据库管理系统,常用于LAMP和LNMP等网站场景中。本教程介绍如何在Linux系统ECS实例上安装、配置以及远程访问MySQL数据库。 目录 背景信息 Alibaba Cloud Linux 2/3、CentO…...
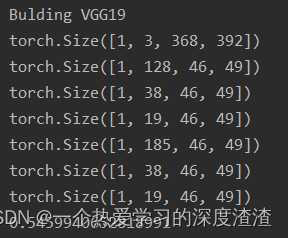
实战——OPenPose讲解及代码实现
一些前提 先思考下面几个问题; 1、什么是姿态估计? 参考:Point Detect任务,识别人体指定部分的关键点; 2、姿态估计中的难点是什么? 从干扰的角度,人体被遮挡对检测的影响很大;…...

专注于创意设计,为您的小程序和网站建设带来更多的可能性
随着移动互联网的快速发展,越来越多的企业开始关注小程序和网站建设,以此来拓展业务和提升品牌形象。 在这个领域中,创意设计扮演着关键的角色。它不仅可以帮助企业打造独特的形象和品牌,还能够提高用户体验和购买决策的效率。 因…...

ATF(TF-A)安全通告 TFV-6 (CVE-2017-5753, CVE-2017-5715, CVE-2017-5754)
ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-6 (CVE-2017-5753, CVE-2017-5715, CVE-2017-5754) 二、Variant 1 (CVE-2017-5753) 三、Variant 2 (CVE-2017-5715) 四、Variant 3 (CVE-2017-5754) 一、ATF(TF-A)安全通告 TFV-6 (CVE-2017-5753, CVE-2017-5715, C…...

vue3 基础语法 02
你好,今天过的怎么样呀,嘿嘿,加油夏 💕 文章目录 一、模板语法 一、模板语法 React的开发模式: React 使用的 jsx,对应的代码编写的类似于js的一种语法;通过 Babel 将 jsx , 编译成…...

版本控制工具——git
版本控制是指对软件开发过程中各种程序代码、配置文件及说明文档等文件变更的管理,是软件配置管理的核心思想之一。 版本控制最主要的功能就是追踪文件的变更。它将什么时候、什么人更改了文件的什么内容等信息忠实地了记录下来。每一次文件的改变,文件的…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...

软件工程教学评价
王海林老师您好。 您的《软件工程》课程成功地将宏观的理论与具体的实践相结合。上半学期的理论教学中,您通过丰富的实例,将“高内聚低耦合”、SOLID原则等抽象概念解释得十分透彻,让这些理论不再是停留在纸面的名词,而是可以指导…...

MySQL用户远程访问权限设置
mysql相关指令 一. MySQL给用户添加远程访问权限1. 创建或者修改用户权限方法一:创建用户并授予远程访问权限方法二:修改现有用户的访问限制方法三:授予特定数据库的特定权限 2. 修改 MySQL 配置文件3. 安全最佳实践4. 测试远程连接5. 撤销权…...
