当前位置： 首页 > news >正文

05应用程序设计和文件操作

news 2026/2/11 2:47:38

一、 给应用程序设置菜单栏

比如：

在qt中，如果想要使用菜单栏功能，那么界面的基类要选择QMainWindow,不能选择QWidget QDialog
实现菜单栏步骤如下：
第一步：在UI设计师，直接双击菜单栏
在这里插入图片描述

第二步：在UI设计师，修改文本内容和其他设置
在这里插入图片描述

进行设置
在这里插入图片描述

设置的效果图如下：
在这里插入图片描述

给菜单选项，增加图片资源
在这里插入图片描述

二、输入对话框(QInputDialog)

让用户比较方便的输入一些单一信息（The QInputDialog class provides a simple convenience dialog to get a single value from the use

相关文章：

05应用程序设计和文件操作

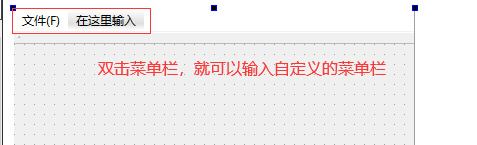
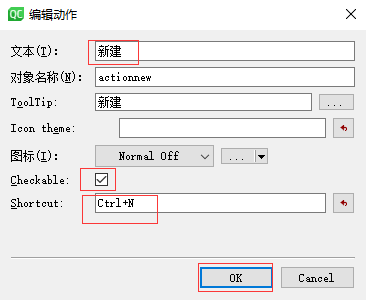
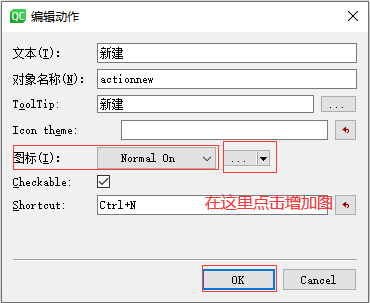
一、 给应用程序设置菜单栏 比如： 在qt中，如果想要使用菜单栏功能，那么界面的基类要选择QMainWindow,不能选择QWidget QDialog 实现菜单栏步骤如下： 第一步：在UI设计师，直接双击菜单栏 第二步：在UI设计师，修改文本内容和其他设置 进行设置 设置的效果图如下： …...

编程日记 2023/8/16 10:55:26

【果树农药喷洒机器人】Part8：果树对靶变量喷药实验

📢：博客主页 【https://blog.csdn.net/weixin_51244852】 📢：文章若有幸对你有帮助，可点赞 👍 收藏 ⭐不迷路🙉 📢：内容若有错误，敬请留言 📝指正…...

编程日记 2023/8/16 10:54:25

framework.beans.factory.annotation.Autowired(required=true)}

将其它项目复制过来，启动后会报错 15:24:55.880 [main] ERROR o.s.b.SpringApplication - [reportFailure,843] - Application run failed org.springframework.beans.factory.UnsatisfiedDependencyException: Error creating bean with name containerDataHandleC…...

编程日记 2023/8/16 10:53:23

【应用笔记】使用 CW32 实现电池备份（VBAT）功能

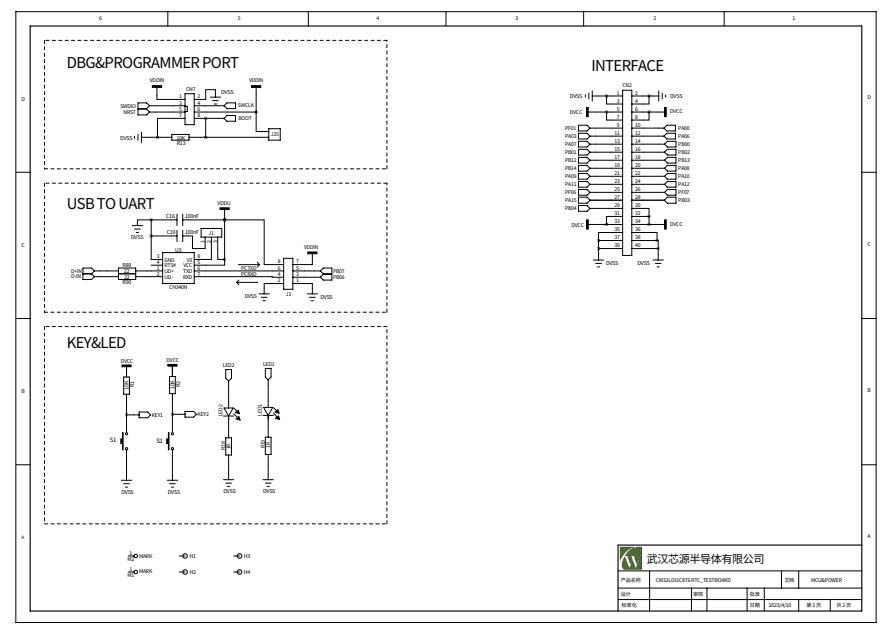
前言 电池备份（VBAT）功能的实现方法，一般是使用 MCU 自带的 VBAT 引脚，通过在该引脚连接钮扣电池，当系统电源因故掉电时，保持 MCU 内部备份寄存器内容和 RTC 时间信息不会丢失。 本文档介绍了如何基于 C…...

编程日记 2023/8/16 10:52:21

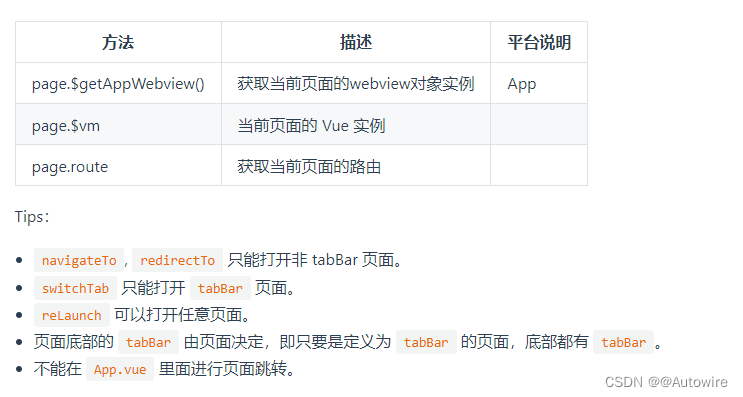
探讨uniapp的navigator 页面跳转问题

navigator 页面跳转。该组件类似HTML中的<a>组件&#xff0c;但只能跳转本地页面。目标页面必须在pages.json中注册。 "tabBar": {"color": "#7A7E83","selectedColor": "#3cc51f","borderStyle": "bl…...

编程日记 2023/8/16 10:51:19

使用Epoll实现高效的多路I/O转接

文章目录 概述1. 理解Epoll机制2. Epoll的三个主要函数3. 基于Epoll实现多路I/O转接4. 总结 概述 在网络编程中&#xff0c;高效地处理大量并发连接是提升系统性能的关键。传统的多线程或多进程模型在这种情况下可能会导致资源消耗过大&#xff0c;而Epoll&#xff08;事件驱动…...

编程日记 2023/8/16 10:50:17

流程挖掘in汽车丨宝马的流程效能提升实例

汽车行业在未来10年里&#xff0c;可能会面临比过去50年更多的变化。电动化、智能化、共享化和自动驾驶等方面的趋势可能给企业流程带来以下挑战&#xff1a; 供应链管理-电动化和智能化的发展可能导致供应链中的零部件和系统结构发生变化&#xff0c;企业需要重新评估和优化供…...

编程日记 2023/8/16 10:49:16

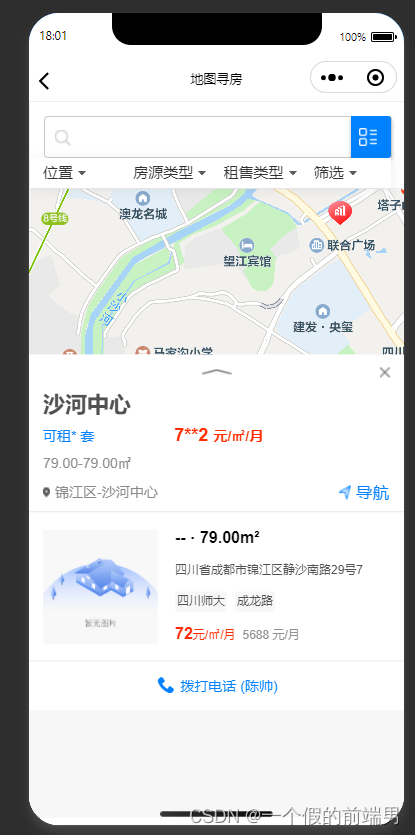
微信小程序实现当前页面更新上一个页面

日常项目中需要实现的一个价格脱敏功能&#xff1a;通过点击页面二中的查看完整信息 点击回退按钮实现页面一中的价格显露出来 通过查询了大量资料发现 大多数都是通过调用上一个接口的onload 或者onshow 实现视图更新 经测试后 发现 无法实现 只能更改数据 无法更新视图 实现…...

编程日记 2023/8/16 10:48:14

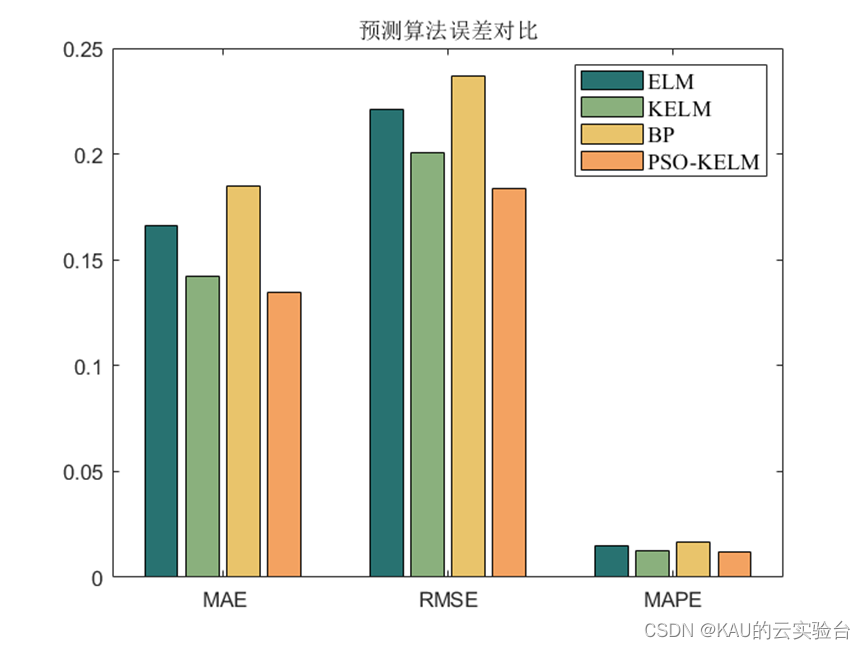
基于PSO-KELM的时间序列数据预测（含对比实验）

前段时间有粉丝私信想让我出一期对时间序列预测的文章&#xff0c;所以今天它来了。 时间序列数据&#xff0c;如股指价格&#xff0c;具有波动性、非线性和突变的特点&#xff0c;对于这类数据的预测往往需要可靠强健的预测模型&#xff0c;而传统的机器学习算法如SVM、BP等…...

编程日记 2023/8/16 10:47:12

线性代数(二) 矩阵及其运算

前言 行列式det(A) 其实表示的只是一个值 ∣ a b c d ∣ a d − b c \begin{vmatrix} a & b\\ c & d\end{vmatrix} ad -bc ​ac​bd​ ​ad−bc&#xff0c;其基本变化是基于这个值是不变。而矩阵表示的是一个数表。 定义 矩阵与线性变换的关系 即得 ( a 11 a 12…...

编程日记 2023/8/16 10:46:11

【图像分类】理论篇（4）图像增强opencv实现

随机旋转 随机旋转是一种图像增强技术&#xff0c;它通过将图像以随机角度进行旋转来增加数据的多样性&#xff0c;从而帮助改善模型的鲁棒性和泛化能力。这在训练深度学习模型时尤其有用&#xff0c;可以使模型更好地适应各种角度的输入。 原图像&#xff1a; 旋转后的图像&…...

编程日记 2023/8/16 10:45:09

Centos下的tcpdump抓包用法

先查一下是否安装, 无的话装一下 (版本低的用yum install) : rpm -qa tcpdump dnf install tcpdump 1. 列出能抓包的网卡: tcpdump -D | --list-interfaces 2. 在eth0网卡上抓来源为10.1.1.1 的包, 只抓一个包 (-n这里是不解析DNS) : tcpdump -i eth0 -n src 10.1.1.1 -…...

编程日记 2023/8/16 10:44:08

自然语言处理从入门到应用——LangChain：记忆（Memory）-[记忆的存储与应用]

分类目录&#xff1a;《自然语言处理从入门到应用》总目录 使用SQLite存储的实体记忆 我们将创建一个简单的对话链&#xff0c;该链使用ConversationEntityMemory&#xff0c;并使用SqliteEntityStore作为后端存储。使用EntitySqliteStore作为记忆entity_store属性上的参数&am…...

编程日记 2023/8/16 10:43:07

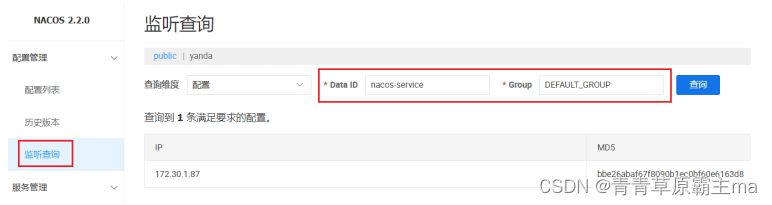
微服务与Nacos概述-5

引入OpenFeign 添加依赖&#xff1a; <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId> </dependency> <dependency><groupId>com.alibaba.cloud</groupId>…...

编程日记 2023/8/16 10:42:05

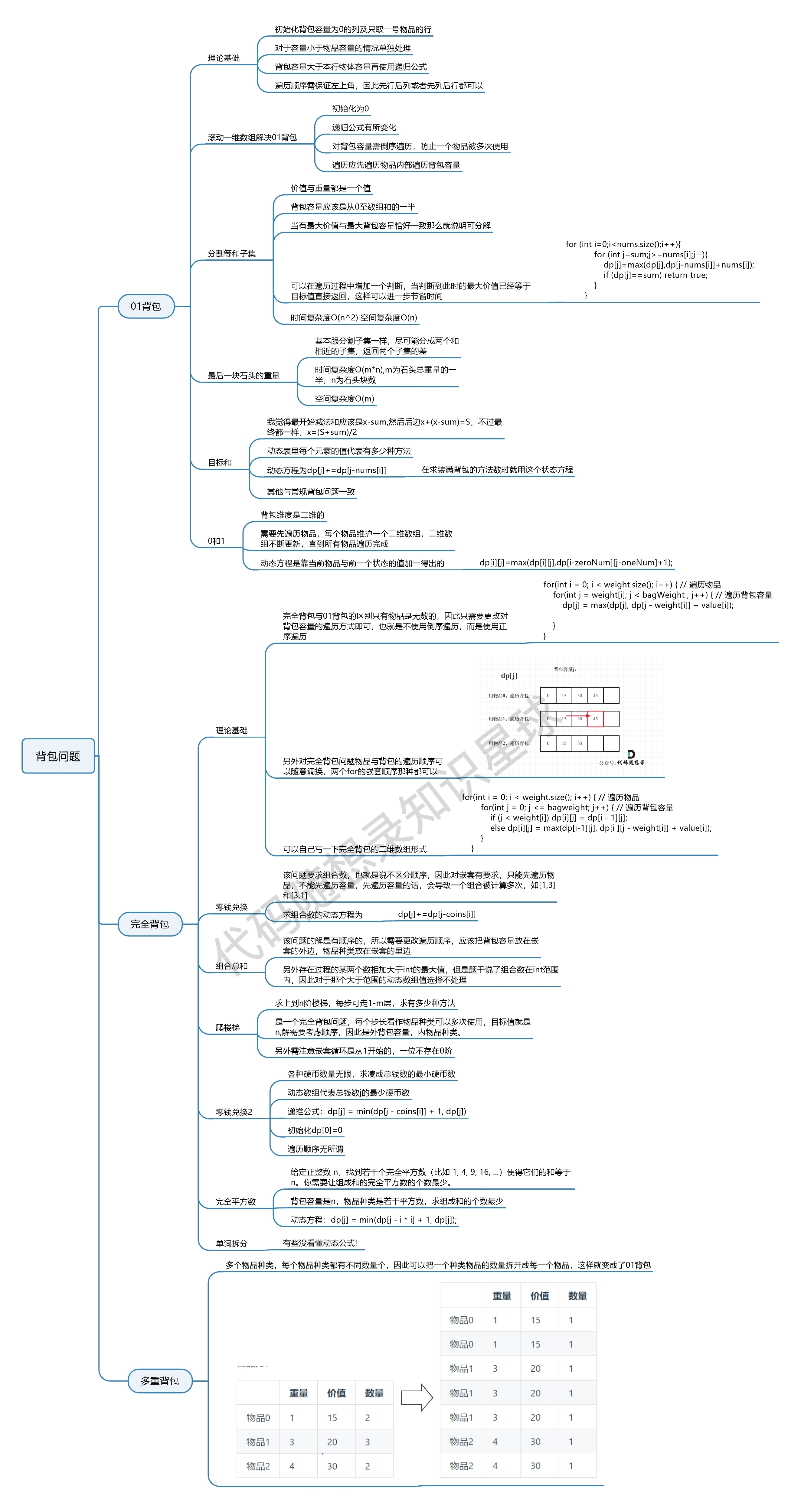
第九章 动态规划part08（代码随想录）

139.单词拆分 1. 确定dp[i][j] dp数组以及下标的含义一维dp数组的递推公式 dp[i] : 字符串长度为i的话&#xff0c;dp[i]为true&#xff0c;表示可以单词能被在字典中出现的单词组成。 dp[s.size()] true; 说明可以利用字典中出现的单词拼接出 s 。 2. 一维dp数组的递推公式…...

编程日记 2023/8/16 10:41:04

智能家居(1)---工厂模式实现灯光控制（继电器组）以及火灾报警模组的封装

采用工厂模式以面向对象的方式来封装各种设备模块&#xff0c;方便整合项目以及后期的维护和扩展 mainPro.c&#xff08;主函数&#xff09; #include <stdio.h> #include "controlDevice.h"struct Devices *pdeviceHead NULL; //设备工厂链…...

编程日记 2023/8/16 10:40:03

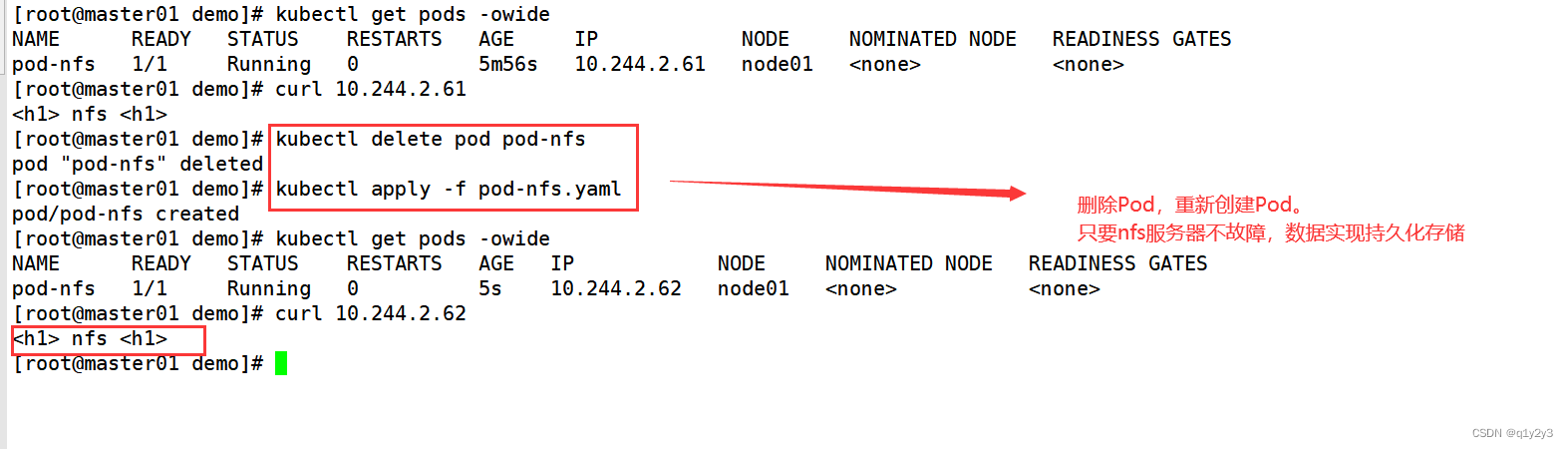
kubernetes的存储卷使用

目录 一、为什么使用存储卷 二、emptyDir存储卷 1.概念 2.创建Pod emptyDir 3. 验证emptyDir存储卷 三、hostPath存储卷 1.概念 2.创建Pod hostPath 3.验证hostPath存储卷 三、nfs共享存储卷 1.概念 2.安装nfs&#xff0c;配置nfs服务 3.创建Pod 4.验证nfs存储卷 一、…...

编程日记 2023/8/16 10:39:00

centos 之安装 openssl 1.1.1报错

源码make时报错&#xff0c;可能是系统的perl的版本太低问题。 [rootlocalhost ~]# cpan -a | grep Test::More Test::More 0.92 1.302171 EXODIST/Test-Simple-1.302171.tar.gz [rootlocalhost ~]# cpan -a | grep Text::Template [rootlocalhost ~]# …...

编程日记 2023/8/16 10:37:56

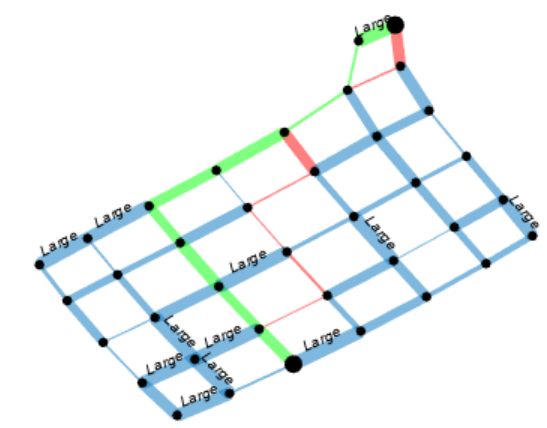
matlab使用教程(16)—图论中图的定义与修改

1.修改现有图的节点和边 此示例演示如何使用 addedge 、 rmedge 、 addnode 、 rmnode 、 findedge 、 findnode 及 subgraph 函数访问和修改 graph 或 digraph 对象中的节点和/或边。 1.1 添加节点 创建一个包含四个节点和四条边的图。s 和 t 中的对应元素用于指定每条…...

编程日记 2023/8/16 10:36:55

【C++面向对象】--- 继承 的奥秘（下篇）

个人主页&#xff1a;平行线也会相交&#x1f4aa; 欢迎 点赞&#x1f44d; 收藏✨ 留言✉ 加关注&#x1f493;本文由 平行线也会相交 原创 收录于专栏【C之路】&#x1f48c; 本专栏旨在记录C的学习路线&#xff0c;望对大家有所帮助&#x1f647;‍ 希望我们一起努力、成长&…...

编程日记 2023/8/16 10:35:53

IDEA运行Tomcat出现乱码问题解决汇总

最近正值期末周&#xff0c;有很多同学在写期末Java web作业时&#xff0c;运行tomcat出现乱码问题&#xff0c;经过多次解决与研究&#xff0c;我做了如下整理&#xff1a; 原因&#xff1a; IDEA本身编码与tomcat的编码与Windows编码不同导致&#xff0c;Windows 系统控制台…...

编程新知 2026/2/10 11:13:58

Xshell远程连接Kali（默认 | 私钥）Note版

前言:xshell远程连接&#xff0c;私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

编程新知 2026/1/28 2:18:42

MongoDB学习和应用(高效的非关系型数据库)

一丶 MongoDB简介 对于社交类软件的功能&#xff0c;我们需要对它的功能特点进行分析&#xff1a; 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具&#xff1a; mysql&#xff1a;关系型数据库&am…...

编程新知 2026/1/23 10:24:30

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别

UnsatisfiedLinkError 在对接硬件设备中&#xff0c;我们会遇到使用 java 调用 dll文件 的情况&#xff0c;此时大概率出现UnsatisfiedLinkError链接错误&#xff0c;原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用&#xff0c;结果 dll 未实现 JNI 协…...

编程新知 2025/10/6 16:38:04

转转集团旗下首家二手多品类循环仓店“超级转转”开业

6月9日&#xff0c;国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解&#xff0c;“超级…...

编程新知 2026/2/8 4:08:40

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序

一、开发环境准备 ​​工具安装​​&#xff1a; 下载安装DevEco Studio 4.0&#xff08;支持HarmonyOS 5&#xff09;配置HarmonyOS SDK 5.0确保Node.js版本≥14 ​​项目初始化​​&#xff1a; ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

编程新知 2026/2/1 4:17:33

Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！

一、引言 在数据驱动的背景下&#xff0c;知识图谱凭借其高效的信息组织能力&#xff0c;正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合&#xff0c;探讨知识图谱开发的实现细节&#xff0c;帮助读者掌握该技术栈在实际项目中的落地方法。 …...

编程新知 2025/9/17 21:39:04

【HTML-16】深入理解HTML中的块元素与行内元素

HTML元素根据其显示特性可以分为两大类&#xff1a;块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

编程新知 2025/11/11 6:28:42

NXP S32K146 T-Box 携手 SD NAND（贴片式TF卡）：驱动汽车智能革新的黄金组合

在汽车智能化的汹涌浪潮中&#xff0c;车辆不再仅仅是传统的交通工具&#xff0c;而是逐步演变为高度智能的移动终端。这一转变的核心支撑&#xff0c;来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒&#xff08;T-Box&#xff09;方案&#xff1a;NXP S32K146 与…...

编程新知 2026/1/24 14:43:35

Qt 事件处理中 return 的深入解析

Qt 事件处理中 return 的深入解析 在 Qt 事件处理中&#xff0c;return 语句的使用是另一个关键概念&#xff0c;它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别&#xff1a;不同层级的事件处理 方…...

编程新知 2025/6/10 21:19:52