OpenCV-Python中的图像处理-傅里叶变换
OpenCV-Python中的图像处理-傅里叶变换
- 傅里叶变换
- Numpy中的傅里叶变换
- Numpy中的傅里叶逆变换
- OpenCV中的傅里叶变换
- OpenCV中的傅里叶逆变换
- DFT的性能优化
- 不同滤波算子傅里叶变换对比
傅里叶变换
- 傅里叶变换经常被用来分析不同滤波器的频率特性。我们可以使用 2D 离散傅里叶变换 (DFT) 分析图像的频域特性。实现 DFT 的一个快速算法被称为快速傅里叶变换( FFT)。
- 对于一个正弦信号:x (t) = A sin (2πft), 它的频率为 f,如果把这个信号转到它的频域表示,我们会在频率 f 中看到一个峰值。如果我们的信号是由采样产生的离散信号组成,我们会得到类似的频谱图,只不过前面是连续的,现在是离散。你可以把图像想象成沿着两个方向采集的信号。所以对图像同时进行 X 方向和 Y 方向的傅里叶变换,我们就会得到这幅图像的频域表示(频谱图)。
- 对于一个正弦信号,如果它的幅度变化非常快,我们可以说他是高频信号,如果变化非常慢,我们称之为低频信号。你可以把这种想法应用到图像中,图像那里的幅度变化非常大呢?边界点或者噪声。所以我们说边界和噪声是图像中的高频分量(注意这里的高频是指变化非常快,而非出现的次数多)。如果没有如此大的幅度变化我们称之为低频分量。
Numpy中的傅里叶变换
Numpy 中的 FFT 包可以帮助我们实现快速傅里叶变换。函数 np.fft.fft2() 可以对信号进行频率转换,输出结果是一个复杂的数组。本函数的第一个参数是输入图像,要求是灰度格式。第二个参数是可选的, 决定输出数组的大小。输出数组的大小和输入图像大小一样。如果输出结果比输入图像大,输入图像就需要在进行 FFT 前补0。如果输出结果比输入图像小的话,输入图像就会被切割。
f = np.fft.fft2(img)
现在我们得到了结果,频率为 0 的部分(直流分量)在输出图像的左上角。如果想让它(直流分量)在输出图像的中心,我们还需要将结果沿两个方向平移 N/2 。函数 np.fft.fftshift() 可以帮助我们实现这一步。(这样更容易分析)。进行完频率变换之后,我们就可以构建振幅谱了。
fshift = np.fft.fftshift(f)
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)# 构建振幅图
magnitude_spectrum = 20*np.log(np.abs(fshift))plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image')
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Magnitude Spectrum')
plt.show()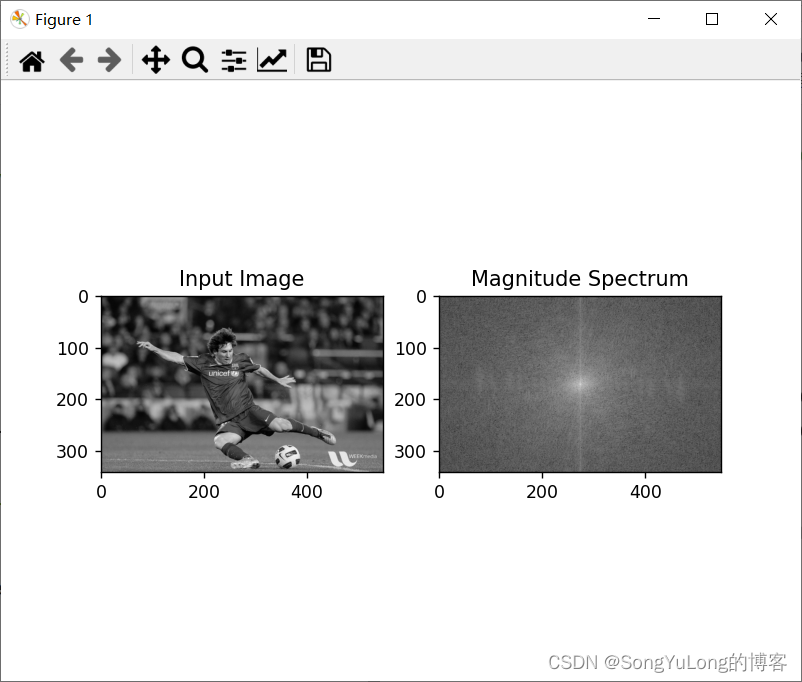
我们可以看到输出结果的中心部分更白(亮),这说明低频分量更多。
Numpy中的傅里叶逆变换
- 对图像进行FFT变换之后得到频域图像数据,然后再做IFFT变换又可以得到原始图像。相关函数:np.fft.ifftshift(),np.fft.ifft2()
fishift = np.fft.ifftshift(fshift)
img_ifft = np.fft.ifft2(fishift) - 我们可以对频域图像数据进行操作以实现一些图像处理效果,如在频域内将低频分量的值设为0,可以实现对图像的高通滤波处理:
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)# 1.在Numpy内对图像进行傅里叶变换,得到其频域图像
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
# 这里是构建振幅图,显示图像频谱
magnitude_spectrum = 20*np.log(np.abs(fshift))# 2.IFFT 将频域图像还原成原始图像,这里只是验证FFT的逆运算
fishift = np.fft.ifftshift(fshift)
img_ifft = np.fft.ifft2(fishift)
img_ifft = np.abs(img_ifft) # 取绝对值,否则不能用imshow()来显示图像# 3.在频域内将低频分量的值设为0,实现高通滤波。
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0 # 4.对高通滤波后的图像频域数据进行逆傅里叶变换,得到高通滤波后图像。
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back) # 取绝对值,否则不能用imshow()来显示图像
# 构建高通滤波后的振幅图,显示图像频谱
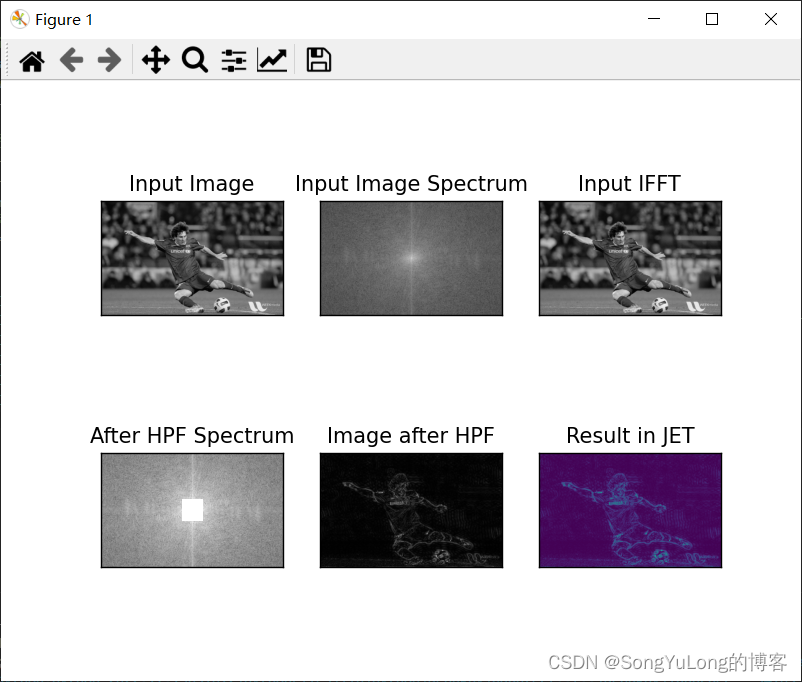
after_sepctrum = 20*np.log(np.abs(fshift))plt.subplot(231), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(232), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Input Image Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(233), plt.imshow(img_ifft, cmap='gray'), plt.title('Input IFFT'), plt.xticks([]), plt.yticks([])
plt.subplot(234), plt.imshow(after_sepctrum, cmap='gray'), plt.title('After HPF Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(235), plt.imshow(img_back, cmap='gray'), plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(236), plt.imshow(img_back), plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()
OpenCV中的傅里叶变换
OpenCV 中相应的函数是 cv2.dft() 和 cv2.idft()。和前面输出的结果一样,但是是双通道的。第一个通道是结果的实数部分,第二个通道是结果的虚数部分。输入图像要首先转换成 np.float32 格式。
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
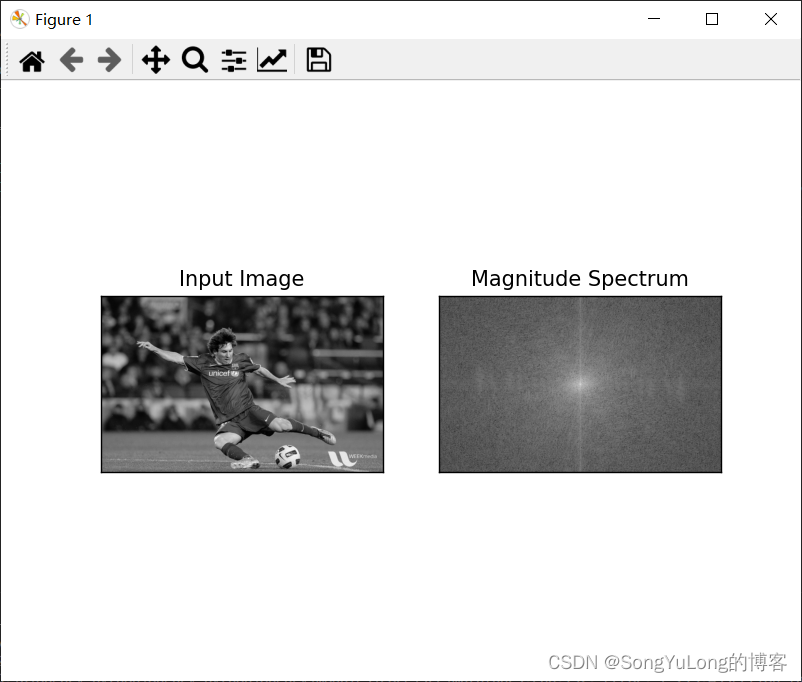
dft_shift = np.fft.fftshift(dft)magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
OpenCV中的傅里叶逆变换
前面的部分我们实现了一个 HPF(高通滤波)高通滤波其实是一种边界检测操作。现在我们来做 LPF(低通滤波)将高频部分去除。其实就是对图像进行模糊操作。首先我们需要构建一个掩模,与低频区域对应的地方设置为 1, 与高频区域对应的地方设置为 0。
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
# 1.OpenCV中做DFT
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)rows, cols = img.shape
crow, ccol = int(rows/2), int(cols/2)# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
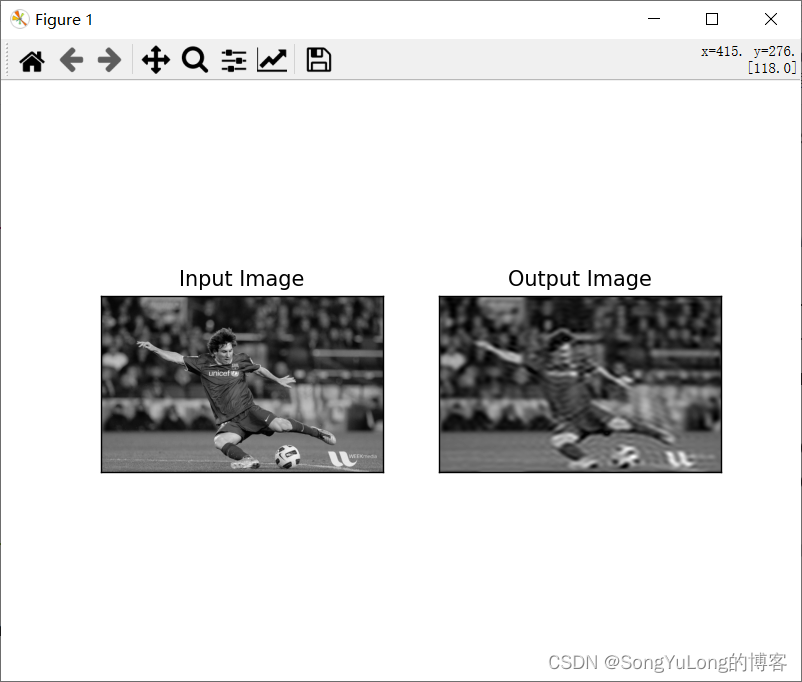
img_back = cv2.magnitude(img_back[:,:,0], img_back[:,:,1])plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(img_back, cmap='gray'), plt.title('Output Image'), plt.xticks([]), plt.yticks([])
plt.show()
DFT的性能优化
- 当数组的大小为某些值时 DFT 的性能会更好。当数组的大小是 2 的指数时 DFT 效率最高。当数组的大小是 2, 3, 5 的倍数时效率也会很高。所以如果你想提高代码的运行效率时,你可以修改输入图像的大小(补 0)。对于OpenCV 你必须自己手动补 0。但是 Numpy,你只需要指定 FFT 运算的大小,它会自动补 0。
- OpenCV 提供了一个函数:cv2.getOptimalDFTSize()来确定最佳大小。它可以同时被 cv2.dft() 和 np.fft.fft2() 使用。
import numpy as np
import cv2img = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
rows,cols = img.shape
print('原始图像大小:',rows, cols)
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print('DFT最佳大小:',nrows, ncols)
原始图像大小: 342 548
DFT最佳大小: 360 576
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
rows,cols = img.shape
print('原始图像大小:',rows, cols)
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print('DFT最佳大小:',nrows, ncols)# Numpy数组操作,原图扩大到最佳DFT size
nimg = np.zeros((nrows, ncols))
nimg [:rows, :cols] = img#
right = ncols - cols
bottom = nrows - rows
# just to avoid line breakup in PDF file
mimg = cv2.copyMakeBorder(img, 0, bottom, 0, right, cv2.BORDER_CONSTANT, value=0)plt.subplot(231), plt.imshow(img, cmap='gray')
plt.subplot(232), plt.imshow(nimg, cmap='gray')
plt.subplot(233), plt.imshow(mimg, cmap='gray')
plt.show()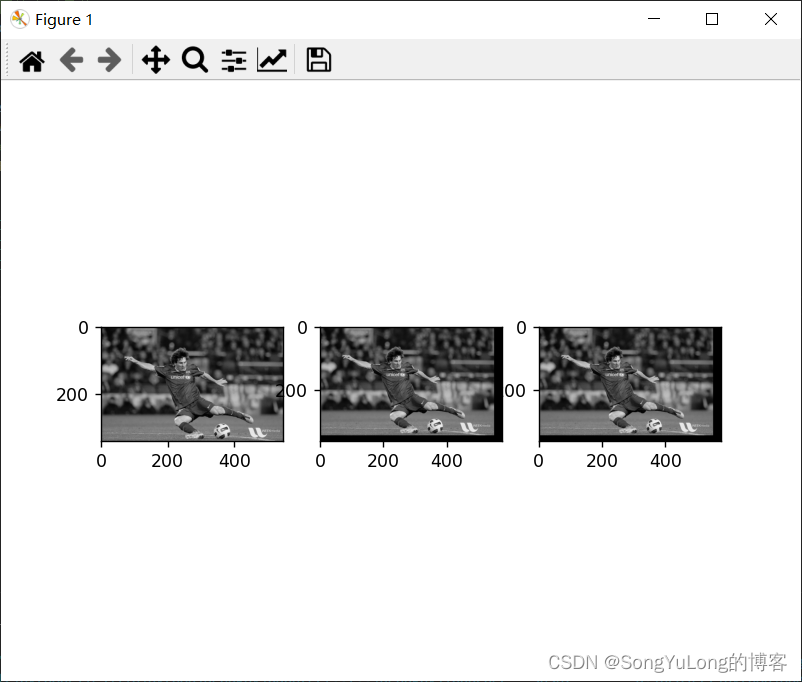
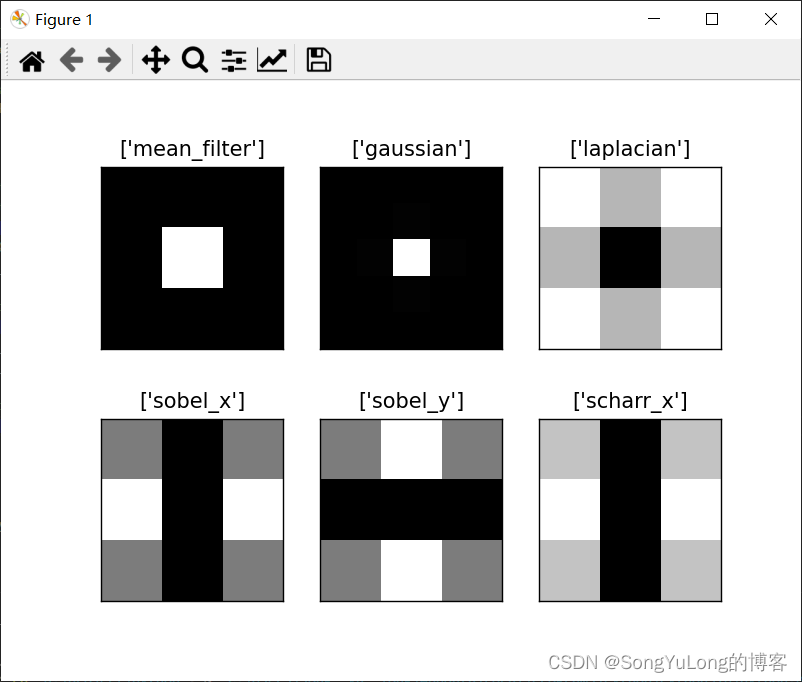
不同滤波算子傅里叶变换对比
为什么拉普拉斯算子是高通滤波器?为什么 Sobel 是 HPF?等等。对于第一个问题的答案我们以傅里叶变换的形式给出。我们一起来对不同的算子进行傅里叶变换并分析它们:
import numpy as np
import cv2
from matplotlib import pyplot as plt# simple averaging filter whitout scaling parameter
mean_filter = np.ones((3,3))# creating a guassian filter
x = cv2.getGaussianKernel(5, 10)
# x.T 为矩阵转置
gaussian = x*x.T# different edge detecting filters
# scharr in x-direction
scharr = np.array([[-3, 0, 3],[-10, 0, 10],[-3, 0, 3]])# sobel in x direction
sobel_x = np.array([[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]])# sobel in y direction
sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])# laplacian
laplacian = np.array([[0, 1, 0], [1, -4, 1],[0, 1, 0]])filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian', 'laplacian', 'sobel_x', 'sobel_y', 'scharr_x']fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]for i in range(6):plt.subplot(2,3,i+1), plt.imshow(mag_spectrum[i], cmap='gray')plt.title([filter_name[i]]), plt.xticks([]), plt.yticks([])
plt.show()
相关文章:

OpenCV-Python中的图像处理-傅里叶变换
OpenCV-Python中的图像处理-傅里叶变换 傅里叶变换Numpy中的傅里叶变换Numpy中的傅里叶逆变换OpenCV中的傅里叶变换OpenCV中的傅里叶逆变换 DFT的性能优化不同滤波算子傅里叶变换对比 傅里叶变换 傅里叶变换经常被用来分析不同滤波器的频率特性。我们可以使用 2D 离散傅里叶变…...

阿里云FRP内网穿透挂载多台服务器
1. FRP介绍 FRP (Fast Reverse Proxy) 是比较流行的一款。FRP 是一个免费开源的用于内网穿透的反向代理应用,它支持 TCP、UDP 协议, 也为 http 和 https 协议提供了额外的支持。你可以粗略理解它是一个中转站, 帮你实现 公网 ←→ FRP(服务器…...

多店铺功能
(一) 系统管理:菜单权限、前台菜单、角色管理、职员管理、登录日志、操作日志、图片空间、商城消息、风格设置、计划任务 (二) 基础设置:商城配置、导航管理、广告管理、广告位置、银行管理、支付管理、地区管理、友情链接、快递管理、消息模板 (三) 会员…...
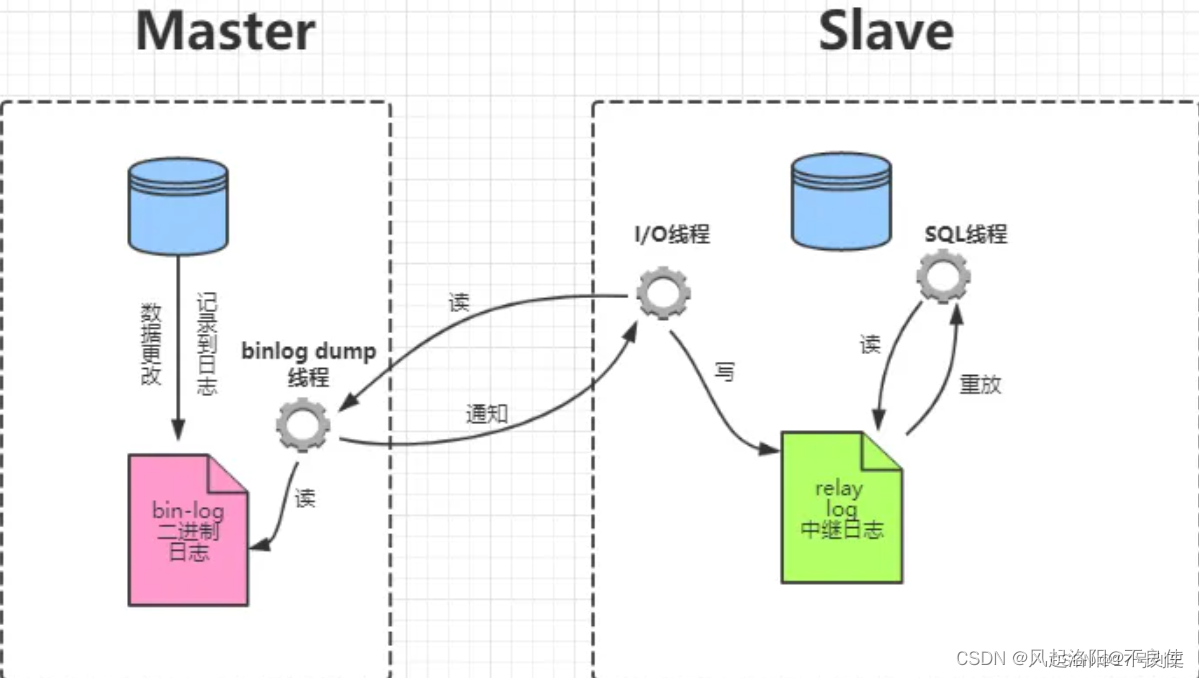
mysql主从复制搭建(一主一从)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言MySQL复制过程分为三部: 一、准备工作二、配置>主库Master三、配置>从库SlaveSlave_IO_Running: YesSlave_SQL_Running: Yes 四、测试至此&am…...
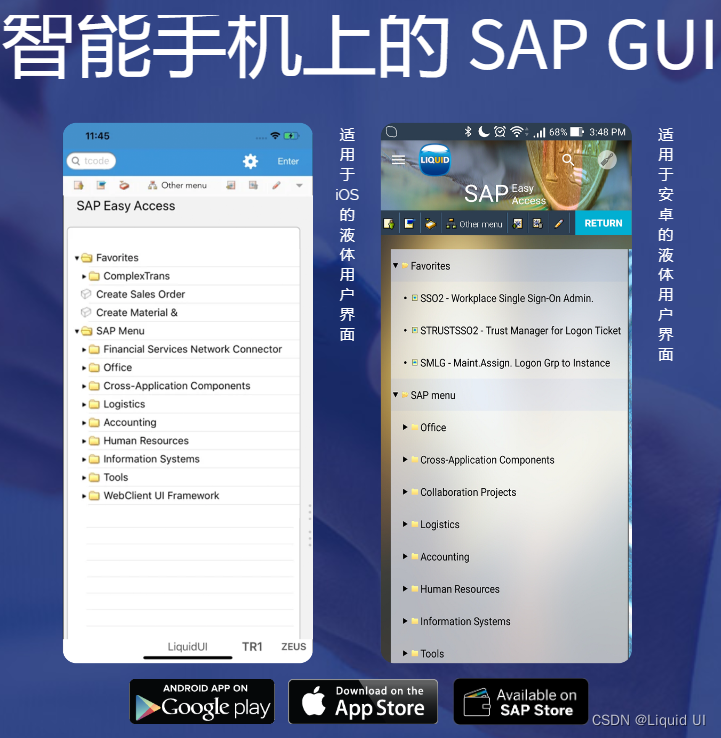
什么是Liquid UI?
热门议题: 1、企业如何快速解决人员移动办公的需求,比如在苹果安卓手机,平板电脑,MAC登录SAP。2、企业如何解决用户经常抱怨的流程复杂,操作繁琐,难以使用等问题 公司介绍: Synactive,Inc. 是…...
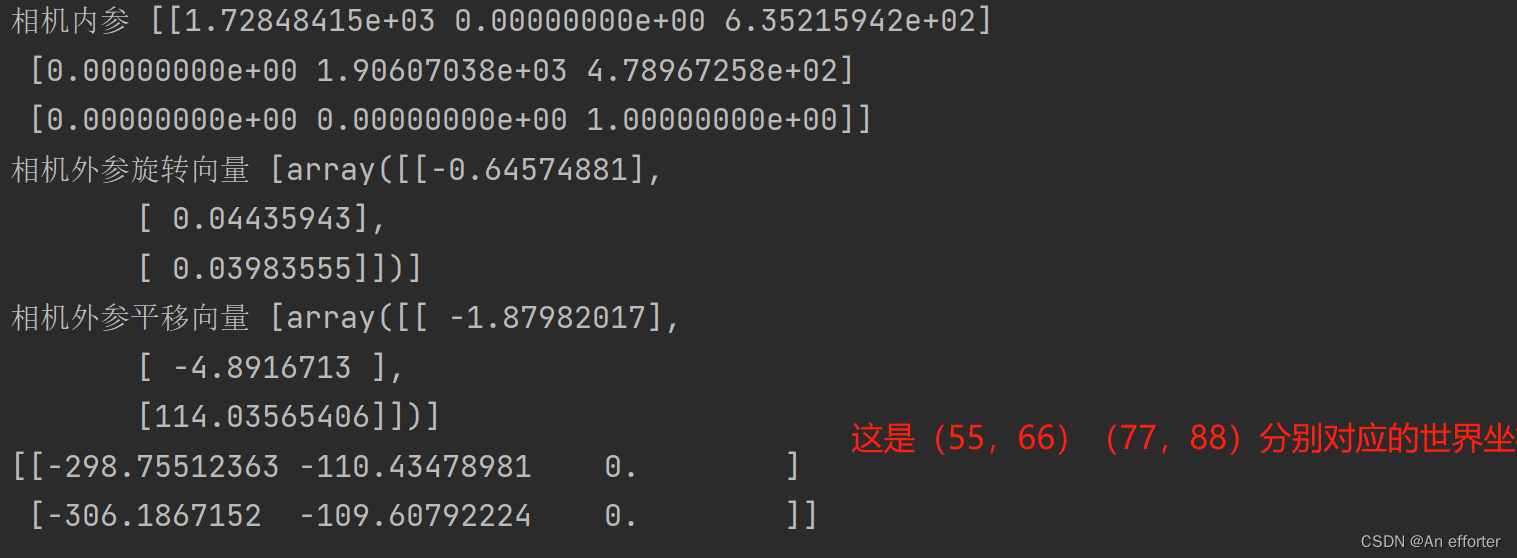
非常详细的相机标定(六)(2维坐标点转为3维坐标点)
根据提取的相机的参数,2维坐标点转为3维坐标点,代码如下: import argparse from argparse import RawTextHelpFormatter import numpy as np import cv2# 寻找焦点 def cam_calib_find_corners(img, rlt_dir, col, row):# 灰度化图片&#x…...
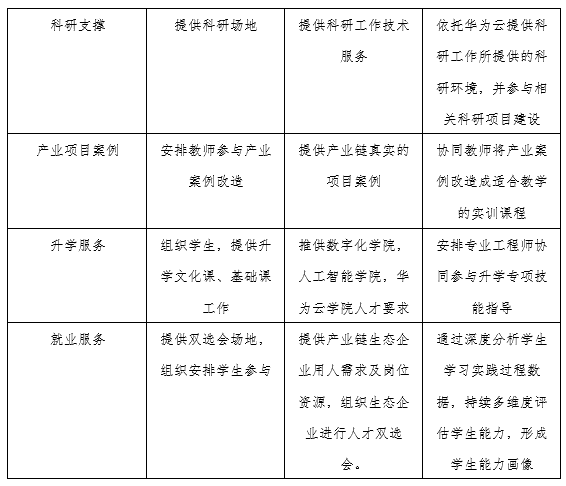
云计算虚拟仿真实训平台
一、云计算虚拟仿真系统概述 云计算虚拟仿真系统是一种基于云计算技术和虚拟化技术的系统,用于实现各种仿真和模拟任务。它可以提供强大的计算能力和资源管理,为用户提供灵活、高效、可扩展的仿真环境。 该系统通常由一组服务器、网络和存储设备组成&am…...

计算机网络:网络字节序
目录 一、字节序1.字节序概念2.字节序的理解(1)大端模式存储数据(2)小端模式存储数据 二、网络字节序 一、字节序 1.字节序概念 字节序:内存中存储多字节数据的顺序。 难道存储数据还要看顺序吗? yes。内…...

2023国赛数学建模A题思路分析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…...
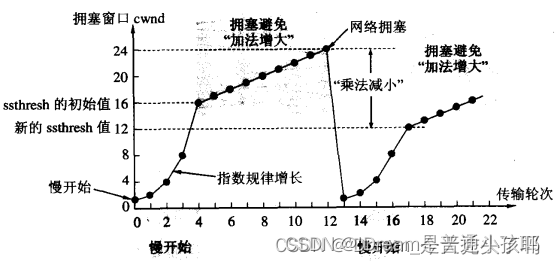
【Java】常见面试题:网络
目录 1. 为什么需要网络协议的分层?2. 【封装和分用】3. Socket套接字主要针对传输层协议划分为如下三类(了解)4. 简单说一下TCP和UDP的区别:5. TCP中的长短连接6. 应用层重点协议7. TCP可靠传输机制(三次握手四次挥手…...

TTS | VocGAN声码器训练自己的数据集
哈喽,今天给大家介绍的是如何使用VocGAN声码器训练自己的数据集。 原文 VocGAN: A High-Fidelity Real-time Vocoder with a Hierarchically-nested Adversarial Network 想要论文解读,请参考我的这篇文章~ 本博客主要包括以下内容: 目录…...

nuxt3--prisma配置
目录 一、初始化二、修改配置三、创建数据库表四、安装Prisma客户端五、查询数据库 一、初始化 npm install prisma typescript ts-node types/node --save-devts-node 用来执行main函数更新数据库 根据实际情况安装,如果不需要的话只需要安装prisma tsconfig.json…...
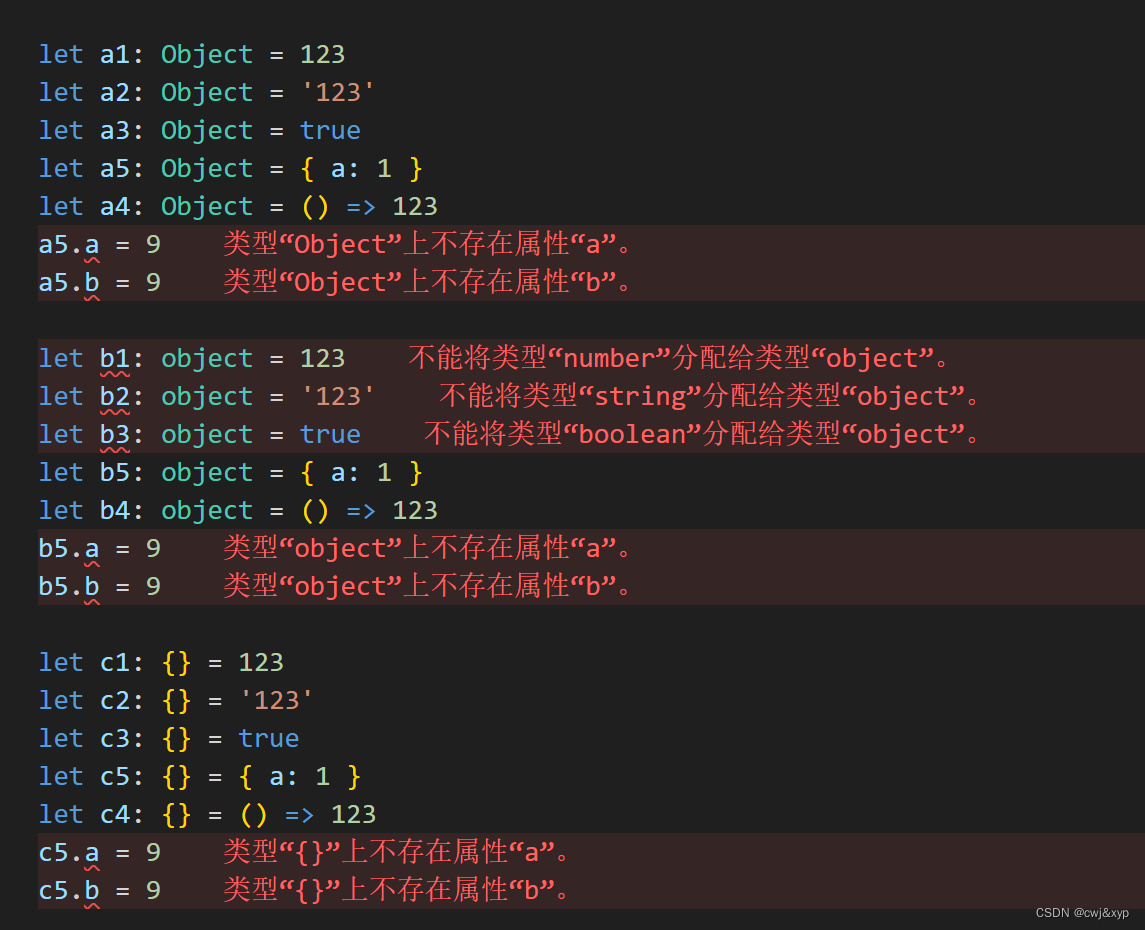
学习ts(一)数据类型(基础类型和任意类型)
运行 起步安装 npm install typescript -g 运行tsc index.ts生成对应的js文件,然后使用node index.js执行js文件 为了方便运行还可以安装插件,ts-node index.ts运行即可 npm i ts-node -g npm init -y npm i types/node -D基本数据类型 // 1.字符…...
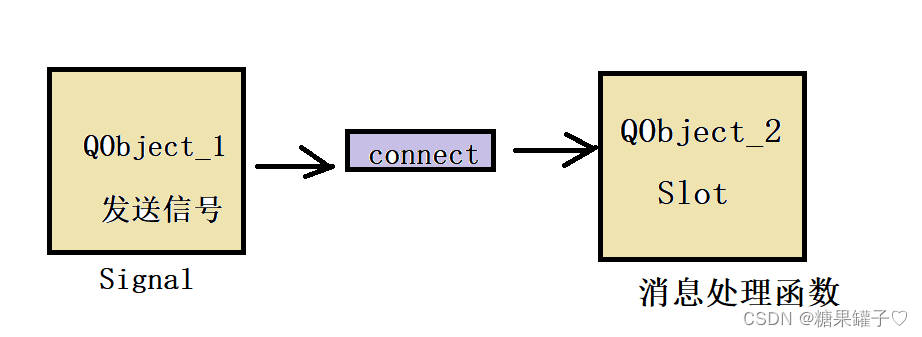
Qt 之 QPushButton,信号与槽机制
文章目录 前言一、QPushButton二、信号与槽机制总结 前言 一、QPushButton 当我们开发基于Qt框架的图形用户界面(GUI)应用程序时,经常需要在界面上添加按钮来实现用户交互。Qt提供了一个名为 QPushButton 的类作为按钮控件的实现。QPushButt…...

MySQL面试题一
MySQL 索引使用有哪些注意事项呢? 可以从两个维度回答这个问题: 索引哪些情况会失效,索引不适合哪些场景 索引哪些情况会失效 查询条件包含or,会导致索引失效。隐式类型转换,会导致索引失效, 例如age字…...

【Java】2021 RoboCom 机器人开发者大赛-高职组(复赛)题解
7-8 人工智能打招呼 号称具有人工智能的机器人,至少应该能分辨出新人和老朋友,所以打招呼的时候应该能有所区别。本题就请你为这个人工智能机器人实现这个功能:当它遇到陌生人的时候,会说:“Hello X, how are you?”其…...

使用electron-vue获取文件夹的路径
使用electron-vue获取文件夹的路径 记录一次开发过程中遇到的bug,我们的项目中需要将vue项目打包为桌面应用软件,为此我们引入了electron框架,在这个过程中,我们需要获取到用户电脑上面文件夹的绝对路径,用这篇文章记…...

剑指Offer14-II.剪绳子II C++
1、题目描述 给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]k[1]…*k[m - 1] 可能的最大乘积是多少?例如&am…...
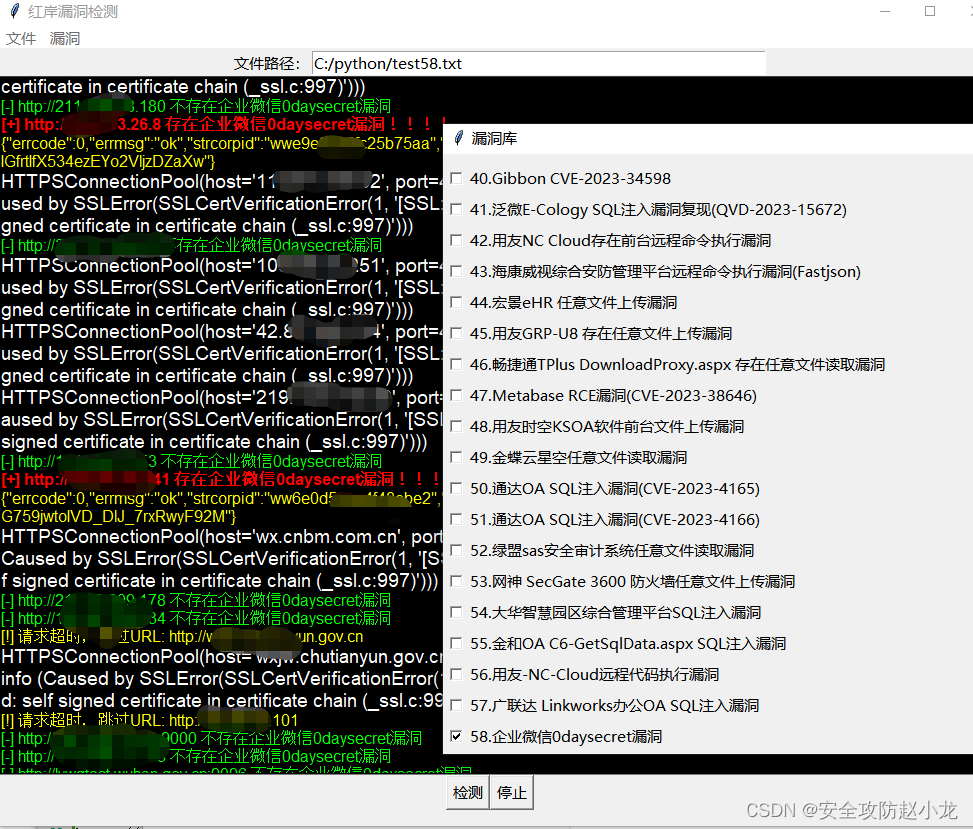
2023企业微信0day漏洞复现以及处理意见
2023企业微信0day漏洞复现以及处理意见 一、 漏洞概述二、 影响版本三、 漏洞复现小龙POC检测脚本: 四、 整改意见 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失&#x…...

【IMX6ULL驱动开发学习】04.应用程序和驱动程序数据传输和交互的4种方式:非阻塞、阻塞、POLL、异步通知
一、数据传输 1.1 APP和驱动 APP和驱动之间的数据访问是不能通过直接访问对方的内存地址来操作的,这里涉及Linux系统中的MMU(内存管理单元)。在驱动程序中通过这两个函数来获得APP和传给APP数据: copy_to_usercopy_from_user …...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
