【C语言】每日一题(多数元素)
多数元素,链接奉上
方法
- 1.摩尔投票
- 2.合理但错误的方法
- 2.1暴力循环
- 2.2排序+求出中间元素中间元素

1.摩尔投票
先来简单的介绍摩尔投票:
摩尔投票是一种用来解决绝对众数问题的算法。
什么是绝对众数呢?
在一个集合中,如果一个元素的出现次数比其他所有元素的出现次数之和还多,那么就称它为这个集合的绝对众数。等价地说,绝对众数的出现次数大于总元素数的一半。
思路:
设置一个计数器
count
利用绝对众数与非绝对众数相互对抗、抵消,
首先遍历数组
遇到相同的count++,不同的count--
在根据count的数值设置当前的candidate(投票对象)
因为绝对众数>非绝对众数,对抗过后剩下的那个元素一定是绝对众数
代码实现:
int majorityElement(int* nums, int numsSize)
{//mooreint i=0;int candidate=nums[0];//设置投票对象int count=1;//因为投票对象是nums[0],本身就是1票for(i=1,count=1;i<numsSize;i++)//遍历数组{if(candidate==nums[i])//当投票对象与当前元素相同时count++count++;else{//否则count--count--;if(count<0)//当投票对象票数<0,重新选择对象{candidate=nums[i];count=1;//票数重置为1}}}return candidate;
}
2.合理但错误的方法
这是题主自己经历的错误,因为超出运行时间,所以不可以用
但是
注意2.2中的方法会根据排序的不同方法而产生不同影响
例如:
冒泡排序会时间出界,但快速排序不会
2.1暴力循环
马有失蹄,暴力循环也会
思路:
设置计数器
count=0
利用外部循环变量作为数组下标,
在内层也设置一个循环变量为数组下标,
与每一个数组元素进行比较,相同时count++当满足count>numssize/2时break
代码实现:
int majorityElement(int* nums, int numsSize)
{int i = 0;for (i = 0; i < numsSize; i++){int count = 0;for (int j = 0; j < numsSize; j++){if (nums[i] == nums[j])count++;}if (count > numsSize / 2)break;}return nums[i];}
2.2排序+求出中间元素中间元素
思路:
先进行排序,之后求出nums[numsSize/2](中间元素),因为绝对众数所占元素必定过半,故中间元素一定为绝对众数,再return中间元素
代码实现:
int majorityElement(int* nums, int numsSize)
{int i = 0;int tmp = 0;for (i = 0; i < numsSize - 1; i++){for (int j = 0; j < numsSize - 1 - i; j++){if (nums[j] > nums[j + 1]){tmp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tmp;}}}return nums[numsSize/2];
}
欢迎讨论哦
相关文章:

【C语言】每日一题(多数元素)
多数元素,链接奉上 方法 1.摩尔投票2.合理但错误的方法2.1暴力循环2.2排序求出中间元素中间元素 1.摩尔投票 先来简单的介绍摩尔投票: 摩尔投票是一种用来解决绝对众数问题的算法。 什么是绝对众数呢? 在一个集合中,如果一个元素…...
)
后端 .net7 Minimal API 限流中间件(微信小程序无师自通十)
我的微信小程序使用.net7 Minimal API 作为后端,当服务器摆上公网后,可以观察到很多的攻击行为和暴力访问。所以,我需要使用微软的限流中间件部署相应的功能在服务器上 关键字: AddFixedWindowLimiter using Microsoft.AspNetCo…...

背上沉重的书包准备面试之react篇
目录 react特性? react生命周期? state和props区别 react中setState执行机制? 在react类组件形式中,setState第二个参数的作用? react事件机制? react事件绑定方式有哪些? react组件之间…...
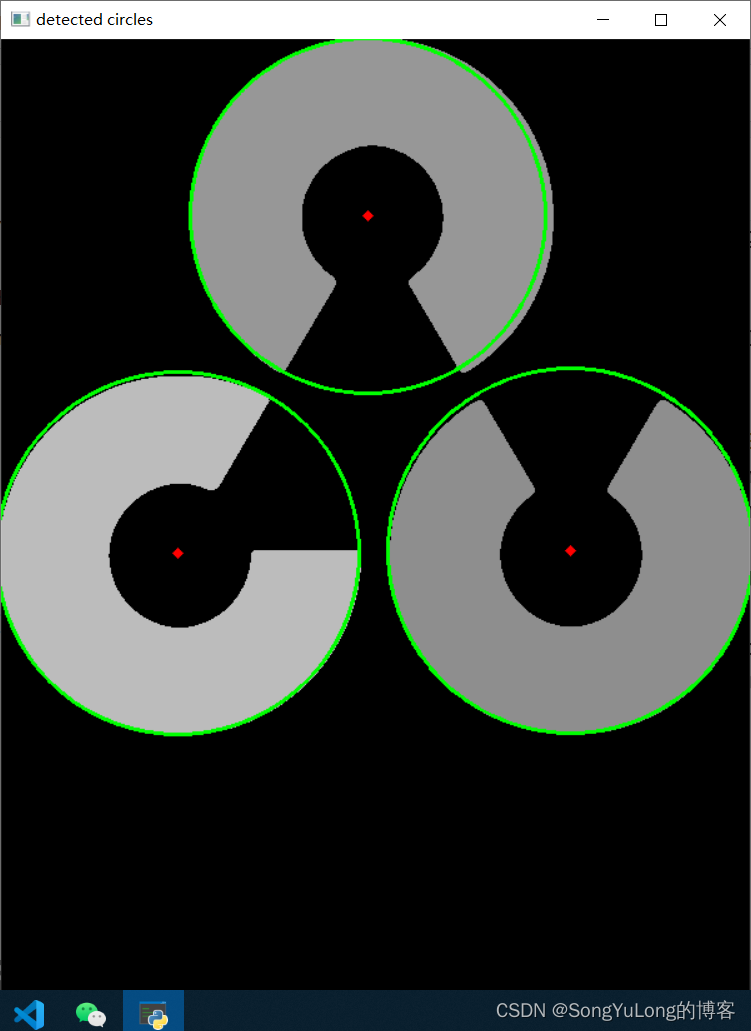
OpenCV-Python中的图像处理-霍夫变换
OpenCV-Python中的图像处理-霍夫变换 霍夫变换霍夫直线变换霍夫圆环变换 霍夫变换 霍夫(Hough)变换在检测各种形状的技术中非常流行,如果要检测的形状可以用数学表达式描述,就可以是使用霍夫变换检测它。即使要检测的形状存在一点破坏或者扭曲也是可以使…...
W5500-EVB-PICO做UDP Client进行数据回环测试(八)
前言 上一章我们用开发板作为UDP Server进行数据回环测试,本章我们让我们的开发板作为UDP Client进行数据回环测试。 连接方式 使开发板和我们的电脑处于同一网段: 开发板通过交叉线直连主机开发板和主机都接在路由器LAN口 测试工具 网路调试工具&a…...
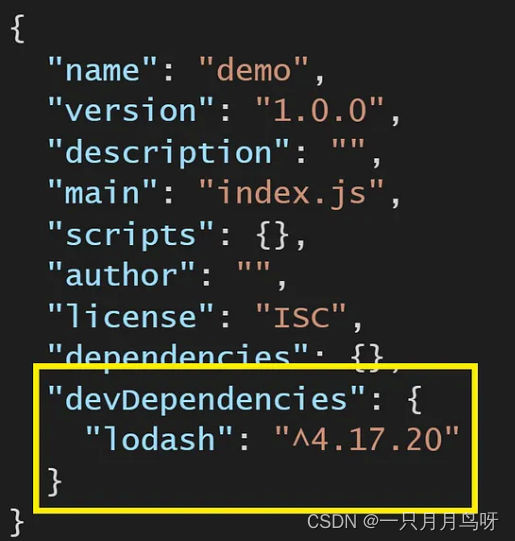
npm install 中 --save 和 --save-dev 是什么?
npm,全名 Node Package Manager,套件管理工具,package.json 会记下你在项目中安装的所有套件。 假设在项目中安装 lodash npm i --save lodash这样在 dependencies 中会出现: 如果修改了导入方式: npm i --save-dev …...

【Nginx17】Nginx学习:目录索引、字符集与浏览器判断模块
Nginx学习:目录索引、字符集与浏览器判断模块 今天要学习的内容有几个还是大家比较常见的,所以学习起来也不会特别费劲。对于目录的默认页设置大家都不会陌生,字符集的设置也比较常见,而浏览器的判断这一块,可能有同学…...

CA/TA开发编程实战-视频课程
Hello大家好,上架一门新的视频课程,课程主要包含两大部分,第一部分搭建环境,第二部分从无到有的编写代码。带领大家"手把手"编写。 具体大纲如下: qemu v8环境搭建 搭建一个qemu_v8的环境,用于…...

(7)(7.1) 使用航点和事件规划任务
文章目录 前言 7.1.1 设置Home位置 7.1.2 视频:制作并保存多路点任务 7.1.3 视频:加载已保存的多航点任务 7.1.4 使用说明 7.1.5 提示 7.1.6 自动网格 7.1.7 任务指令 7.1.8 任务结束 7.1.9 任务重置 7.1.10 MIS_OPTIONS 7.1.11 任务再出发 …...

OCR相关模块——版面分析技术、表格文本识别
OCR相关模块——版面分析技术、表格文本识别 版面分析技术表格识别技术 版面分析技术 版面分析模型:飞桨用到了yolov2检测模型,对文档图片中的文本、表格、图片、标题与列表区域进行检测。当前主流是用分割做。 表格识别技术 参考博文...
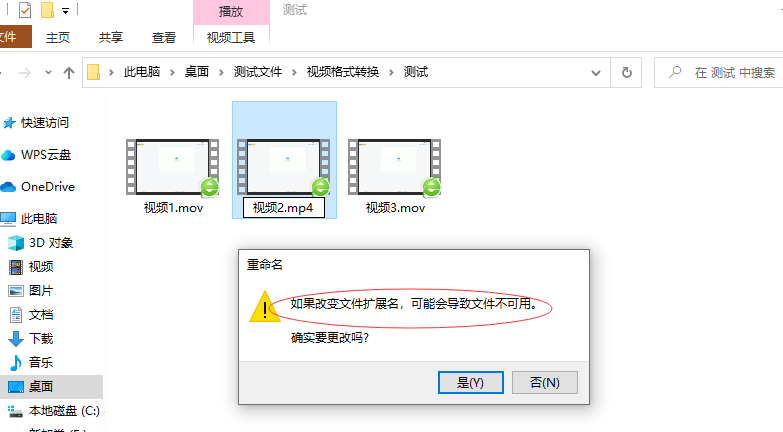
mov转mp4格式怎么转?
mov转mp4格式怎么转?众所周知,MOV视频格式是由苹果公司推出的常用的视频格式,能够在苹果软件及设备上使用。但是,如果将其应用于其他软件和设备上的话,可能会遇到文件无法正常播放的情况。在这个时候,我们需…...
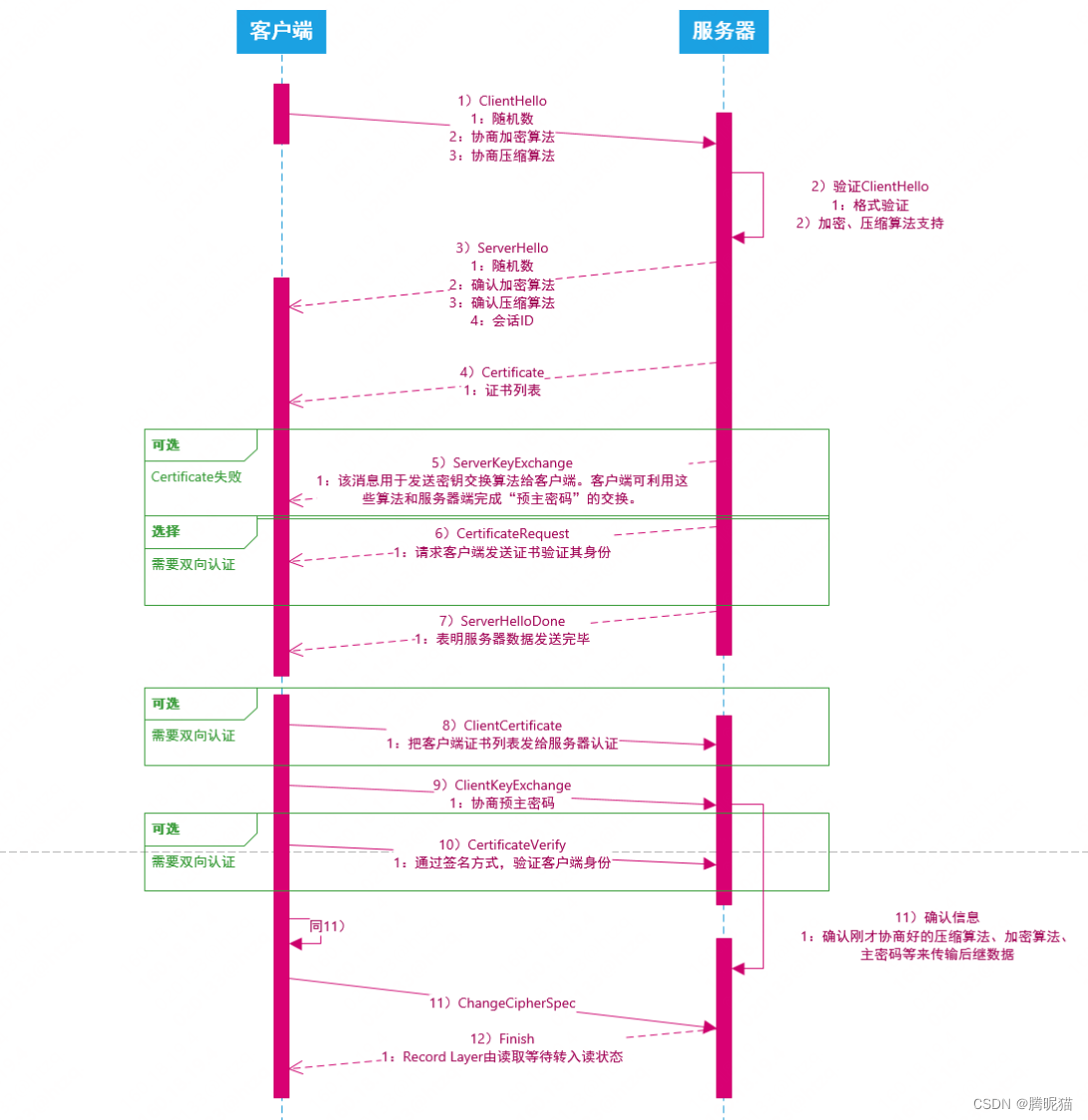
SSL握手协议相关概念
下图为握手协议的流程图,具体的解释参考博客: 【下】安全HTTPS-全面详解对称加密,非对称加密,数字签名,数字证书和HTTPS_tenfyguo的博客-CSDN博客 下面梳理一下SSL协议中的一些细节。首先是相关名词:证书、…...

idea 打开java项目后新建的模块中,java文件夹需要变成蓝色,以及resources文件夹变成三条杠的
idea 打开java项目后新建的模块中,java文件夹需要变成蓝色,以及resources文件夹变成三条杠的方法 再选择modules,找到需要变蓝的文件夹,点击sources即可 同理resources文件夹变成三条杠也只需要找到对应文件夹,点击re…...

【Docker】Docker network之bridge、host、none、container以及自定义网络的详细讲解
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,目前学习C/C、算法、Python、Java等方向,一个正在慢慢前行的普通人。 🏀系列专栏:陈童学的日记 💡其他专栏:CSTL&…...
滑模控制器理论推导和matlab/simulink实例分享
滑模控制的运动轨迹主要分为两个方面:(1)系统的任意初始状态向滑模面运动阶段;(2)系统到达滑模面后并且慢慢趋于稳定的阶段。所以,对于滑模变结构控制器的设计,对应于系统运动的两个阶段,可以分为两个部分:…...

git 操作
git切换ssh和http协议 切换协议: 查看当前remote git remote -v 切换到http: git remote set-url https://github.com/username/repository.git 切换到ssh: git remote set-url gitgithub.com:username/repository.git 某些文件不想提交…...
自建hexo博客并将原有的文章发布其上
1、保存粘贴到memo9中的博客文章,并将txt转换成word文档 varPowerShellPath, CommandLine: string; // , ScriptPath begin//save to txtMemo9.Lines.SaveToFile(test.txt);memo10.Lines.SaveToFile(txt2word.ps1);//save as docxPowerShellPath : powershell.exe…...

【双指针_和为 s 的两个数_C++】
和为s的两个数字 class Solution { public:vector<int> twoSum(vector<int>& nums, int target) {int n nums.size();int left 0;int right n-1;while(left<right){if(nums[left]nums[right]>target) right--;else if(nums[left]nums[right]<tar…...
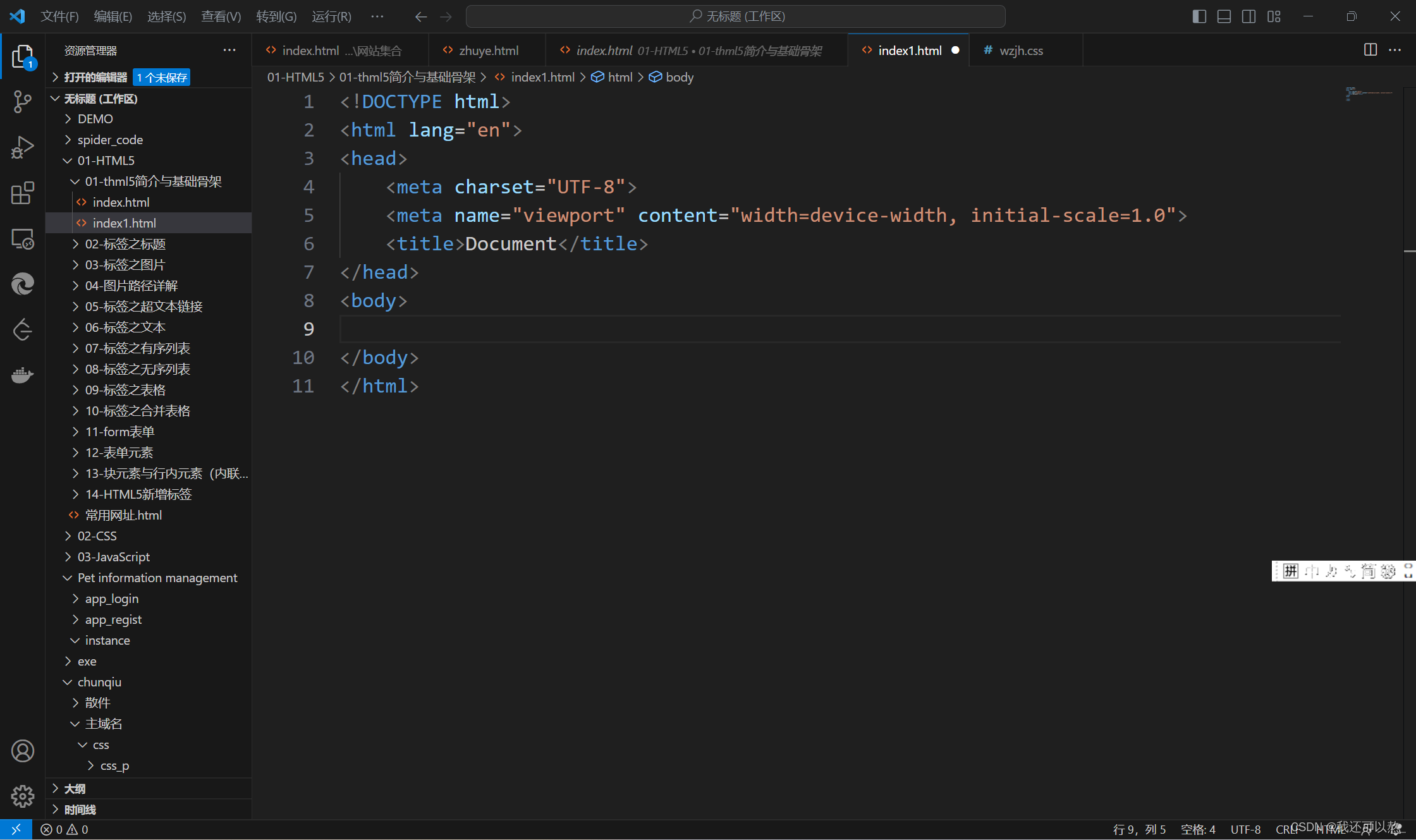
HTML5的介绍和基本框架
目录 HTML5 HTML5介绍 HTML5的DOCTYPE声明 HTML5基本骨架 html标签 head标签 body标签 title标签 meta标签 在vscode中写出第一个小框架 HTML5 HTML5介绍 HTML5是用来描述网页的一种语言,被称为超文本标记语言。用HTML5编写的文件,后缀以.ht…...
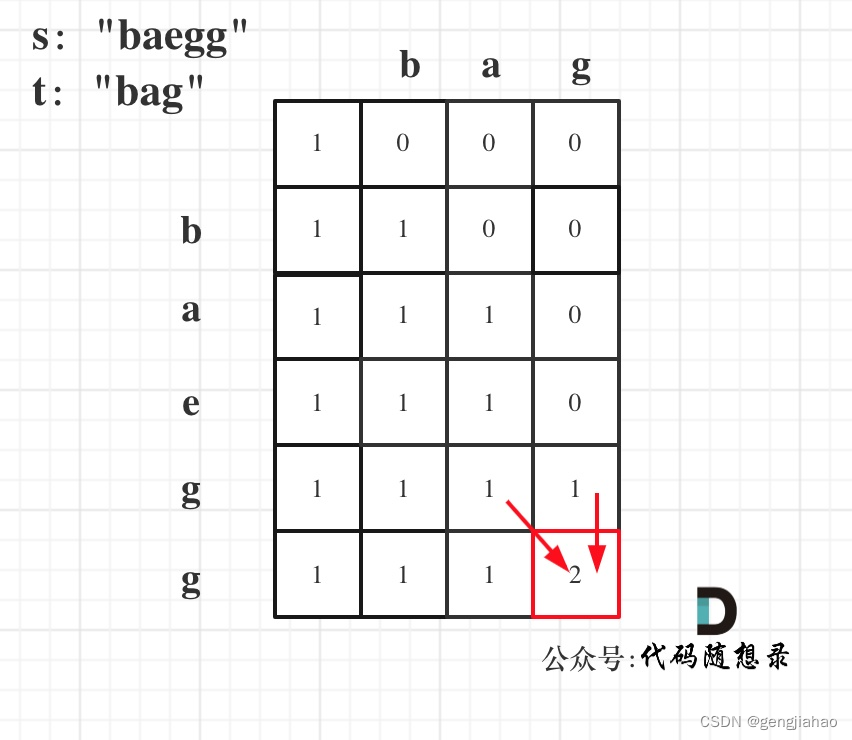
代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列
代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列 392.判断子序列 392.判断子序列 思路: (这道题也可以用双指针的思路来实现,时间复杂度也是O(n)) 这道题应该算是编辑距…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
