wordpress获取最新发布列表/独立站seo外链平台
关于大数值金额大写转换，在财务管理的应用方面没什么意义。一般来说，千亿级，万亿级的数值就够了。因为在国家级层面是以亿为单位的，也就表达为千万亿，万万亿。在企业层面数值金额转换设置到千亿、万亿就行了。大的集团级企业扩大到万万亿也就行了。做企业应用软件的可根据需要设置。至于再大的数值就是天文数字，有另外的表达方法。
本人喜欢探索各种算法。前些天写了15位数值的金额大写转换。今再尝试写一个更多位数值的换算大写转换。提供给需要的同道参考。
金额大写应用在很多方面，如支票、发票、各种单据，各种财务凭证，合同文本金额部分。财务方面制定了一套标准的表达法。财务上金额大写是没有负数的，财务上分借方和贷方，负数就是借方红字和贷方红字，也就是赤字。大写转换的算法要按财务管理的标准来设置。本文详细介绍算法的要点。
算法的要点：
简单地讲就是字串转换处理。若输入是数值型则转为字串型。
将输入的金额分成整数部分和小数部分，整数部分分段为4位数的万级段，再按金额数值逐位转换成中文，拼成大写字串，然后输出。
对于不含零的情况，直接就转换好了。然而对于含零和连续多个零的情况就要消除多余的零。本文介绍的算法就是 ”截数值位消零法”，或称 ”截位消零法” 。
要处理的是整数部分，分四步：
一是 将整数部分分成整数的前几位字段和后面的4位万级数字段，
二是 按字段先换成2个字符的数字和单位的中文表达，
三是 按2个字符截取字段， 将含零的字段消去单位，
四是 处理多余的零，然后拼接整数和小数，输出大写。
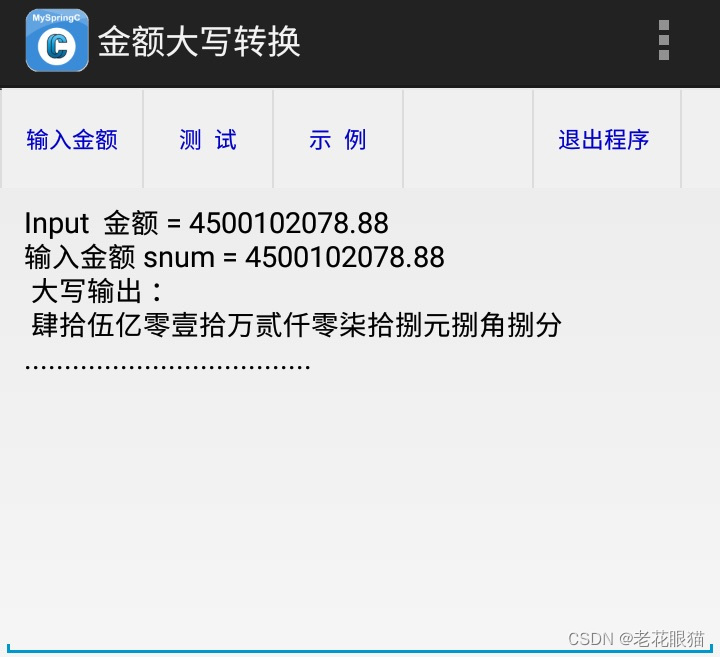
转换的算法就一个函数：
Function convert (){ //传入 snum $ 输出金额大写 put$
// M$="零元拾佰仟万拾佰仟亿拾佰仟兆拾佰仟京拾佰仟" ;
M$="零元拾佰仟万拾佰仟亿拾佰仟万拾佰仟万拾佰仟" ;
string pn$[50] ;
string dn[8] ; //中国式以每万为段，4位一段
//对输入字串截取整数部分和小数部分，
//小数部分直接转换，整数部分按万级分段，
//先处理整数的前几位，后处理后续的4位万级数，
//最后拼接字串输出金额大写
//snum="10020005600205" ; //test
g$= subString (snum, 0 ,1 ) ;
//输入 "0.56" format > " .56"
if(g$=="0") snum= subString (snum,1, 3) ;
nlen=len(snum) ;
n=nlen ;
for (i=0; i<nlen ; i++){
g$= subString (snum, i,1 ) ;
if(g$==".") n= i ; }
if (nlen-n>2) sn$=subString (snum,n+1,2) ;
if (nlen-n==2) sn$=subString (snum,n+1,1)+"0" ;
if (nlen-n==0) sn$="00" ; //无小数
fn$=subString (snum,0,n) ; //截取整数部分
print "输入金额 snum = ", snum ;
// print "整数部分 fn = ", fn$ ; //test
// print "小数角分 sn = ", sn$ ;
//开始转换，先处理整数 fn$ ******
chb$="" ; chs$="" ; chsd$="" ;
//角分小数部分 ******
d1$=subString(sn$,0,1) ;
d2$=subString(sn$,1,1) ;
// print d1$ +" "+d2$ ; //test
if (d1$=="0" ){
c$="零" ; }else{
a$=d1$ ;
snToD ();
c$=c$+"角" ; }
d$ =c$ ;
if (d2$=="0" ){
c$="整" ; }else{
a$=d2$ ;
snToD ();
c$=c$+"分" ; }
d$ =d$+c$ ;
chs$=d$ ; //小数chs$已转换
// print "chs$ = "+chs$ ; //test
if (d1$=="0"&&d2$=="0" ){ chs$="整" ; }
//开始转换，处理整数 fn$ ******
//4位段整数转换
nlen=len (fn$) ; //字串长度
n=nlen/4 ; //整数后4字数段位数
k=nlen-nlen/4*4 ; //mod 整数前几位
// print "Input fn$ = " + fn$ ; //test
// print "长串前面几位 k = " , k ;
// print "长串后 4 字段 n = " , n ;
d1$=subString (fn$, 0, k) ;
d2$=subString (fn$, k, nlen) ;
// print "d1$ = " + d1$ ; //test
// print "d2$ = " + d2$ ;
//整数前几位转换
for (i=0; i<k ; i++){ //
a$= subString (d1$, i, 1 ) ;
snToD () ; //数字转大写 得c$
b$=subString (M$, k - i+n*4,1) ;
p$=subString (N$, n*4+i, 1) ;
chsd$=chsd$+c$+b$ ; } //整数前几位
// print "chsd$ = " + chsd$ ; //test
//**** 整数前几位完成 chsd$
p$="" ;
for (i=0; i<n ; i++){ //整数后4数段位截串
dn[i]= subString (d2$, i*4 , 4 ) ;
p$=p$+ dn[i] +"" ; }
// print "p$ = "+p$ ; //test
int du ; // 4 位数段
for (du=0; du<n ; du++){ //按整数4数段位转换
p$="" ;
for (i=0; i<4 ; i++){ //
a$= subString (dn[du], i, 1 ) ;
snToD () ; //数字转大写 得c$
b$=subString (M$, n*4-du*4 - i ,1) ; //单位
p$=p$+c$+b$ ;
pn$[i]=c$+b$ ; } //整数后4字数段
chb$=chb$+p$ ; } //du
chb$=chsd$+chb$ ;
// print "chb$ = "+chb$ ; //含零整数完成test
//***************
p$=" " ;
nlen=len (chb$)/2 ; //按中文二字组字串
// for (i=0; i<30 ; i++){ pn$[i]=" " ; }
for (i=0; i<nlen ; i++){
pn$[i]=subString(chb$, i*2, 2) ; }
//按位数转换成大写 format 消单位 **********
p1$="" ; p2$="" ;
p$="" ;
for (k=0; k<nlen ; k++){
p1$=pn$[k] ;
if (p1$=="零仟") { pn$[k]="零" ; }
if (p1$=="零佰") { pn$[k]="零" ; }
if (p1$=="零拾") { pn$[k]="零" ; }
if (p1$=="零元") { pn$[k]="元" ; }
if (p1$=="零万") { pn$[k]="万" ; }
if (p1$=="零亿") { pn$[k]="亿" ; }
} //format
p$="" ;
for (m=0; m<nlen ; m++){ //重组整数部分>去零
p$=p$+pn$[m] ; }
// print p$ ; //test
nlen= len (p$) ;
for (i=0; i<nlen ; i++){ //renew p$
pn$[i]=subString(p$, i, 1) ; }
for (m=0; m<nlen ; m++){ //去多余 ”零”
p1$=pn$[m] ;
if (p1$=="零"&&pn$[m+1]=="零" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="元" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="万" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="亿" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="兆" ) { pn$[m]="" ; }
}
// print p1$ ; //test
chb$=" " ;
for (i=0; i<nlen ; i++){ //去零后重组整数部分
chb$=chb$+pn$[i] ; }
//特殊情况100000902 大写： 壹亿万零玖佰零贰元整
//测试时碰到此例 ”壹亿万零... ” 要消 "万" ****
//用京兆需要下列代码，用万亿、万万亿不需要
nlen= len (chb$) ;
for (i=0; i<nlen ; i++){ //特殊情况，消”万” ”亿”
a$=subString (chb$, i, 1 ) ;
b$=subString (chb$, i+1, 1 ) ;
if (a$=="亿"&&b$=="万") {
a$=subString (chb$, 1, i) ;
b$=subString (chb$, i+2, nlen-i ) ;
chb$= a$+b$ ; }
if (a$=="兆"&&b$=="亿") {
a$=subString (chb$, 1, i) ;
b$=subString (chb$, i+2, nlen-i ) ;
chb$=chb$+a$+b$ ; } }
nlen= len (chb$) ;
for (i=0; i<nlen ; i++){ //特殊情况，消”万”
a$=subString (chb$, i, 1 ) ;
b$=subString (chb$, i+1, 1 ) ;
if (a$=="兆"&&b$=="万") {
a$=subString (chb$, 1, i) ;
b$=subString (chb$, i+2, nlen-i ) ;
chb$=chb$+a$+b$ ; } }
chb$=chb$+chs$ ; //整数小数拼接，完成转换
if (snum=="."||snum==".0"||snum==".00"||snum=="0."||snum==" ") {
chb$= " 零元整" ; }
//输出结果 ******
print " 大写输出：" ;
put$=chb$ ;
print put$ ; //转换完成输出
print "...................................." ;
}//convert ()
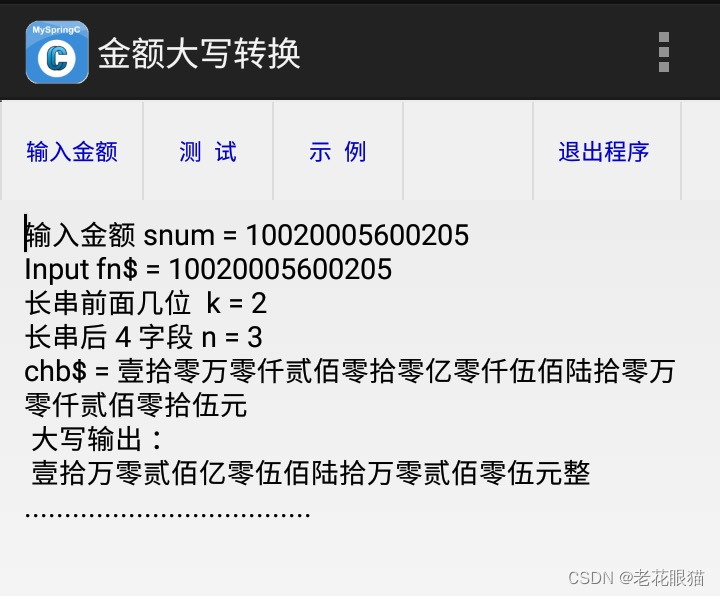
//以下是完整的设计测试源码：
// **** 财务金额大写显示 **************
// 本代码是用简单的 C 语言写的，用 MySpringC
// v2.7 编译调试通过。可以 VB6, C++, Java 改写。
// 编译人：张纯叔（micelu@126.com ）
//*******************************************
string sBarDes[10];
int nBarId[10];
string snum, put$ ; //传入金额，输出大写
int n, i, j, k, m ;
string N$ , M$, D$ ; //预设置大写字符
string a$, c$; //转换 传入a$ 输出c$
string d$, d1$, d2$ ; //计算小数角分
string fn$, sn$ ; //整数字串，小数字串
string chs$, chb$, chsd$ ; //小写，大写，整数首段
int nlen ; //Len 字数
string b$, g$, p$, p1$, p2$ ; //计算
main(){
setDisplay (0);
sBarDes[0]="输入金额";
nBarId[0]=100;
sBarDes[1]=" 测 试 ";
nBarId[1]=101;
sBarDes[2]=" 示 例 ";
nBarId[2]=102;
sBarDes[3]=" ";
nBarId[3]=103;
sBarDes[4]="退出程序 ";
nBarId[4]=104;
setToolBarHeight(10);
setButtonTextSize(15);
setToolBarBackgroundColor(255,220,220,220);
setButtonColor(255,240,240,240);
setButtonTextColor(255,0,0,200);
setToolBar(100,myToolBarProc,sBarDes,nBarId,6);
setTitle("金额大写转换");
while (){}
}//main ()
convert (){ //传入 snum $ 输出金额大写 put$
// M$="零元拾佰仟万拾佰仟亿拾佰仟兆拾佰仟京拾佰仟" ;
M$="零元拾佰仟万拾佰仟亿拾佰仟万拾佰仟万拾佰仟" ;
string pn$[50] ;
string dn[8] ; //中国式以每万为段，4位一段
//对输入字串截取整数部分和小数部分，
//小数部分直接转换，整数部分按万级分段，
//先处理整数的前几位，后处理后续的4位万级数，
//最后拼接字串输出金额大写
//snum="10020005600205" ; //test
g$= subString (snum, 0 ,1 ) ;
//输入 "0.56" format > " .56"
if(g$=="0") snum= subString (snum,1, 3) ;
nlen=len(snum) ;
n=nlen ;
for (i=0; i<nlen ; i++){
g$= subString (snum, i,1 ) ;
if(g$==".") n= i ; }
if (nlen-n>2) sn$=subString (snum,n+1,2) ;
if (nlen-n==2) sn$=subString (snum,n+1,1)+"0" ;
if (nlen-n==0) sn$="00" ; //无小数
fn$=subString (snum,0,n) ; //截取整数部分
print "输入金额 snum = ", snum ;
// print "整数部分 fn = ", fn$ ; //test
// print "小数角分 sn = ", sn$ ;
//开始转换，先处理整数 fn$ ******
chb$="" ; chs$="" ; chsd$="" ;
//角分小数部分 ******
d1$=subString(sn$,0,1) ;
d2$=subString(sn$,1,1) ;
// print d1$ +" "+d2$ ; //test
if (d1$=="0" ){
c$="零" ; }else{
a$=d1$ ;
snToD ();
c$=c$+"角" ; }
d$ =c$ ;
if (d2$=="0" ){
c$="整" ; }else{
a$=d2$ ;
snToD ();
c$=c$+"分" ; }
d$ =d$+c$ ;
chs$=d$ ; //小数chs$已转换
// print "chs$ = "+chs$ ; //test
if (d1$=="0"&&d2$=="0" ){ chs$="整" ; }
//开始转换，处理整数 fn$ ******
//4位段整数转换
nlen=len (fn$) ; //字串长度
n=nlen/4 ; //整数后4字数段位数
k=nlen-nlen/4*4 ; //mod 整数前几位
// print "Input fn$ = " + fn$ ; //test
// print "长串前面几位 k = " , k ;
// print "长串后 4 字段 n = " , n ;
d1$=subString (fn$, 0, k) ;
d2$=subString (fn$, k, nlen) ;
// print "d1$ = " + d1$ ; //test
// print "d2$ = " + d2$ ;
//整数前几位转换
for (i=0; i<k ; i++){ //
a$= subString (d1$, i, 1 ) ;
snToD () ; //数字转大写 得c$
b$=subString (M$, k - i+n*4,1) ;
p$=subString (N$, n*4+i, 1) ;
chsd$=chsd$+c$+b$ ; } //整数前几位
// print "chsd$ = " + chsd$ ; //test
//**** 整数前几位完成 chsd$
p$="" ;
for (i=0; i<n ; i++){ //整数后4数段位截串
dn[i]= subString (d2$, i*4 , 4 ) ;
p$=p$+ dn[i] +"" ; }
// print "p$ = "+p$ ; //test
int du ; // 4 位数段
for (du=0; du<n ; du++){ //按整数4数段位转换
p$="" ;
for (i=0; i<4 ; i++){ //
a$= subString (dn[du], i, 1 ) ;
snToD () ; //数字转大写 得c$
b$=subString (M$, n*4-du*4 - i ,1) ; //单位
p$=p$+c$+b$ ;
pn$[i]=c$+b$ ; } //整数后4字数段
chb$=chb$+p$ ; } //du
chb$=chsd$+chb$ ;
// print "chb$ = "+chb$ ; //含零整数完成test
//***************
p$=" " ;
nlen=len (chb$)/2 ; //按中文二字组字串
// for (i=0; i<30 ; i++){ pn$[i]=" " ; }
for (i=0; i<nlen ; i++){
pn$[i]=subString(chb$, i*2, 2) ; }
//按位数转换成大写 format 消单位 **********
p1$="" ; p2$="" ;
p$="" ;
for (k=0; k<nlen ; k++){
p1$=pn$[k] ;
if (p1$=="零仟") { pn$[k]="零" ; }
if (p1$=="零佰") { pn$[k]="零" ; }
if (p1$=="零拾") { pn$[k]="零" ; }
if (p1$=="零元") { pn$[k]="元" ; }
if (p1$=="零万") { pn$[k]="万" ; }
if (p1$=="零亿") { pn$[k]="亿" ; }
} //format
p$="" ;
for (m=0; m<nlen ; m++){ //重组整数部分>去零
p$=p$+pn$[m] ; }
// print p$ ; //test
nlen= len (p$) ;
for (i=0; i<nlen ; i++){ //renew p$
pn$[i]=subString(p$, i, 1) ; }
for (m=0; m<nlen ; m++){ //去多余 ”零”
p1$=pn$[m] ;
if (p1$=="零"&&pn$[m+1]=="零" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="元" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="万" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="亿" ) { pn$[m]="" ; }
if (p1$=="零"&&pn$[m+1]=="兆" ) { pn$[m]="" ; }
}
// print p1$ ; //test
chb$=" " ;
for (i=0; i<nlen ; i++){ //去零后重组整数部分
chb$=chb$+pn$[i] ; }
//特殊情况100000902 大写： 壹亿万零玖佰零贰元整
//测试时碰到此例 ”壹亿万零... ” 要消 "万" ****
//用京兆需要下列代码，用万亿、万万亿不需要
nlen= len (chb$) ;
for (i=0; i<nlen ; i++){ //特殊情况，消”万” ”亿”
a$=subString (chb$, i, 1 ) ;
b$=subString (chb$, i+1, 1 ) ;
if (a$=="亿"&&b$=="万") {
a$=subString (chb$, 1, i) ;
b$=subString (chb$, i+2, nlen-i ) ;
chb$= a$+b$ ; }
if (a$=="兆"&&b$=="亿") {
a$=subString (chb$, 1, i) ;
b$=subString (chb$, i+2, nlen-i ) ;
chb$=chb$+a$+b$ ; } }
nlen= len (chb$) ;
for (i=0; i<nlen ; i++){ //特殊情况，消”万”
a$=subString (chb$, i, 1 ) ;
b$=subString (chb$, i+1, 1 ) ;
if (a$=="兆"&&b$=="万") {
a$=subString (chb$, 1, i) ;
b$=subString (chb$, i+2, nlen-i ) ;
chb$=chb$+a$+b$ ; } }
chb$=chb$+chs$ ; //整数小数拼接，完成转换
if (snum=="."||snum==".0"||snum==".00"||snum=="0."||snum==" ") {
chb$= " 零元整" ; }
//输出结果 ******
print " 大写输出：" ;
put$=chb$ ;
print put$ ; //转换完成输出
print "...................................." ;
}//convert ()
test (){ //数值含零空位算法测试
clearOutput ();
print "特殊数值检测检验：" ;
snum="20000100300000000" ;
convert () ;
snum="100000902" ;
convert () ;
snum="20005600205" ;
convert () ;
snum="3060002065" ;
convert () ;
snum="10508005.75" ;
convert () ;
snum="50700650.5" ;
convert () ;
snum="1802065.06" ;
convert () ;
}//test ()
sample (){
clearOutput ();
print "输出示例：" ;
snum="30600702" ;
convert () ;
snum="1500903.08" ;
convert () ;
snum="1020697.00" ;
convert () ;
snum="159533.65" ;
convert () ;
snum="282581697.50" ;
convert () ;
snum="520967.56248" ;
convert () ;
snum="2801697.00" ;
convert () ;
}//sample()
snToD (){ //传入a$ 返回c$
N$="零壹贰叁肆伍陆柒捌玖" ;
if (a$=="0") c$=subString (N$,0,1) ;
if (a$=="1") c$=subString (N$,1,1) ;
if (a$=="2") c$=subString (N$,2,1) ;
if (a$=="3") c$=subString (N$,3,1) ;
if (a$=="4") c$=subString (N$,4,1) ;
if (a$=="5") c$=subString (N$,5,1) ;
if (a$=="6") c$=subString (N$,6,1) ;
if (a$=="7") c$=subString (N$,7,1) ;
if (a$=="8") c$=subString (N$,8,1) ;
if (a$=="9") c$=subString (N$,9,1) ;
}//snToD ()
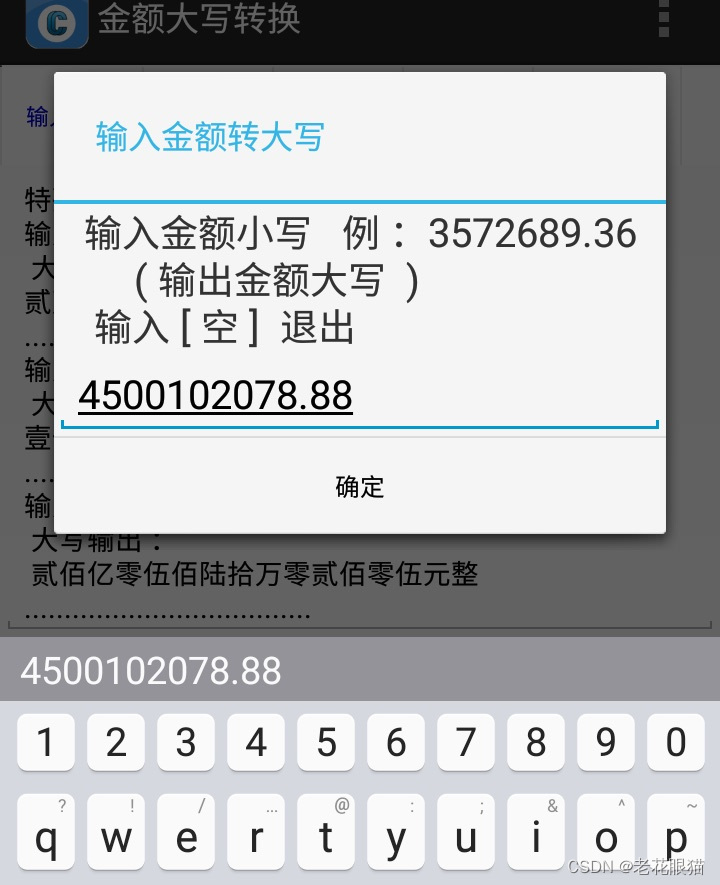
input (){//输入
string m;
snum=stringInput (" 输入金额转大写 "," 输入金额小写 例： 3572689.36 \n ( 输出金额大写 )\n 输入 [ 空 ] 退出 " ) ;
clearOutput ();
print "Input 金额 = ",snum ;
if (snum=="") { snum=".00" ;
print "输入为空，请重新输入。 " ; }
convert () ;
}//input ()
myToolBarProc(int nBtn,int nContext) {
if(nBtn==100){//输入金额
input (); }
if(nBtn==101){ //test 测试
test () ; }
if(nBtn==102){//示例
sample (); }
if(nBtn==103){//算法测试
// convert () ;
}
if(nBtn==104){//退出程序
clearOutput();
exit (0); }
}//myToolbar ()
//**** End ****
相关文章：
大数值金额大写转换（C语言）
关于大数值金额大写转换，在财务管理的应用方面没什么意义。一般来说，千亿级，万亿级的数值就够了。因为在国家级层面是以亿为单位的，也就表达为千万亿，万万亿。在企业层面数值金额转换设置到千亿、万亿就行了。大的集团…...
迷宫问题图解 : 基于骨架提取、四邻域
目录 1. 迷宫的连通域 2. How to remove branch ？ 3. 基于4邻域的 remove 分支 3.1 找到分支的端点 3.2 4邻域的 remove 分支 3.3 循环移除分支 3.4 code 4. 迷宫路线 4.1 预处理 4.2 提取骨架 4.3 分支的端点 4.4 去除分支的端点 4.5 循环去除分支 4…...
设计模式 - 如何在库和主程序之间互相调用数据和函数
背景：在项目开发过程中，难免碰到这种情况，当我们想要通过我们开发的库，调用主程序中的一些变量或者函数的时候，就会导致一些问题，因为在项目构建过程中，库都是不依赖于主程序编译的，…...
Redis面试题：1~2亿条数据需要缓存，请问如何设计这个存储案例
目录 前言 一、哈希取余分区 优点 缺点 二、一致性哈希算法分区 背景 步骤 ① 算法构建一致性哈希环 ② 服务器IP节点映射 ③ key落到服务器的落键规则 优点 ① 容错性 ② 扩展性 缺点 三、哈希槽分区 前言 单机单台100%不可能，肯定是分布式存储&am…...
程序员必备的软技能-《如何阅读一本书》
阅读很重要，我们真的会阅读吗？ 这本书的初版是 1940年，时隔 80年，其内容仍然不过时。第一次读这本书时，给我最大的影响就是主题阅读，每次学习一个新理论、技术，都入手多本关于这项理论、技术的书…...
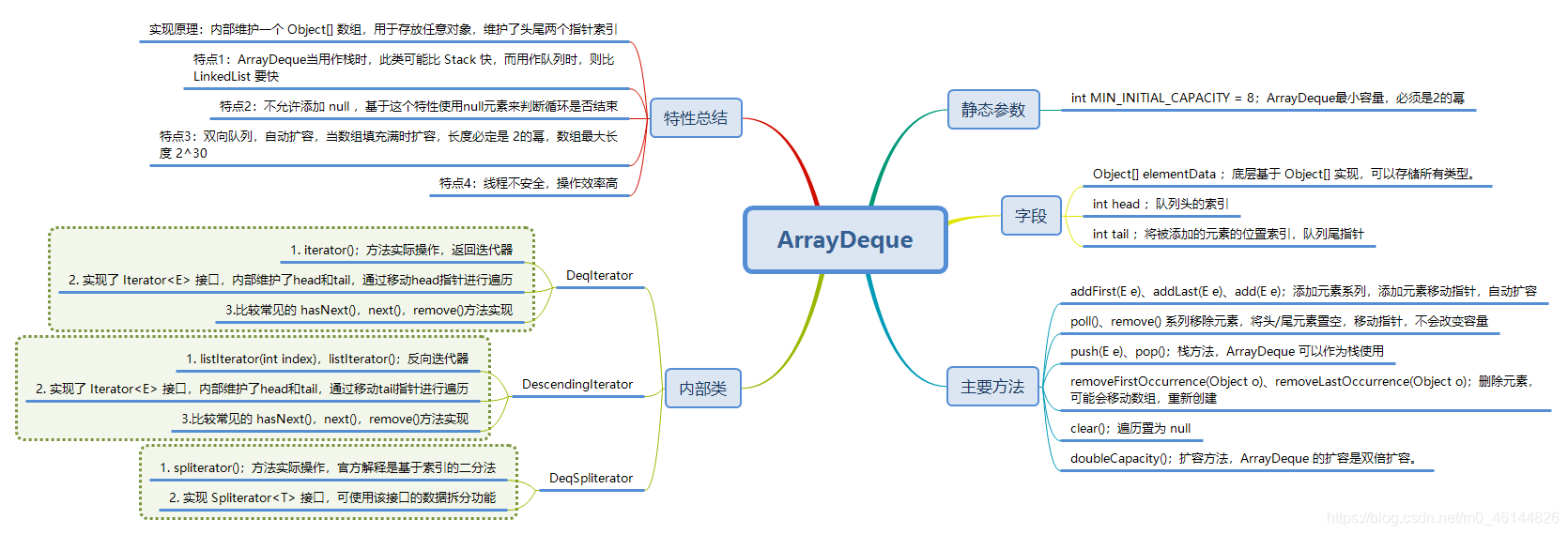
Java数据结构-栈、队列常用类（Stack、ArrayDeque、LinkedLList）
数据结构的三要素包括：逻辑结构、存储结构、数据的运算。逻辑结构描述的是数据之间的逻辑关系，分为线性结构（线性表（数组、链表）、栈、队列）和非线性结构（图、树、集合）。物理结构也…...
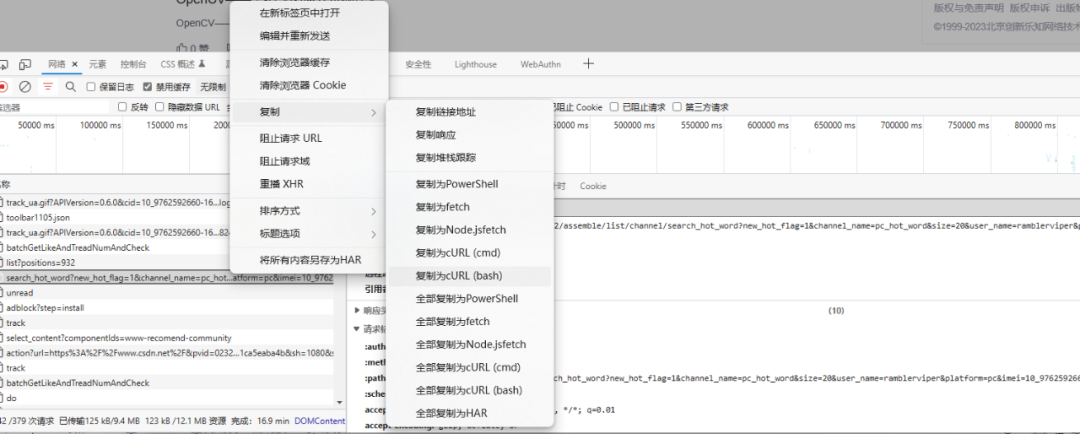
拯救了大批爬虫程序员，因为一个简单的神器
相信大家应该都写过爬虫，简单的爬虫只需要使用 requests 即可。遇到复杂的爬虫，就需要在程序里面加上请求头和参数信息。类似这种：我们一般的步骤是，先到浏览器的网络请求中找到我们需要的请求，然后将请求头和参数信息…...
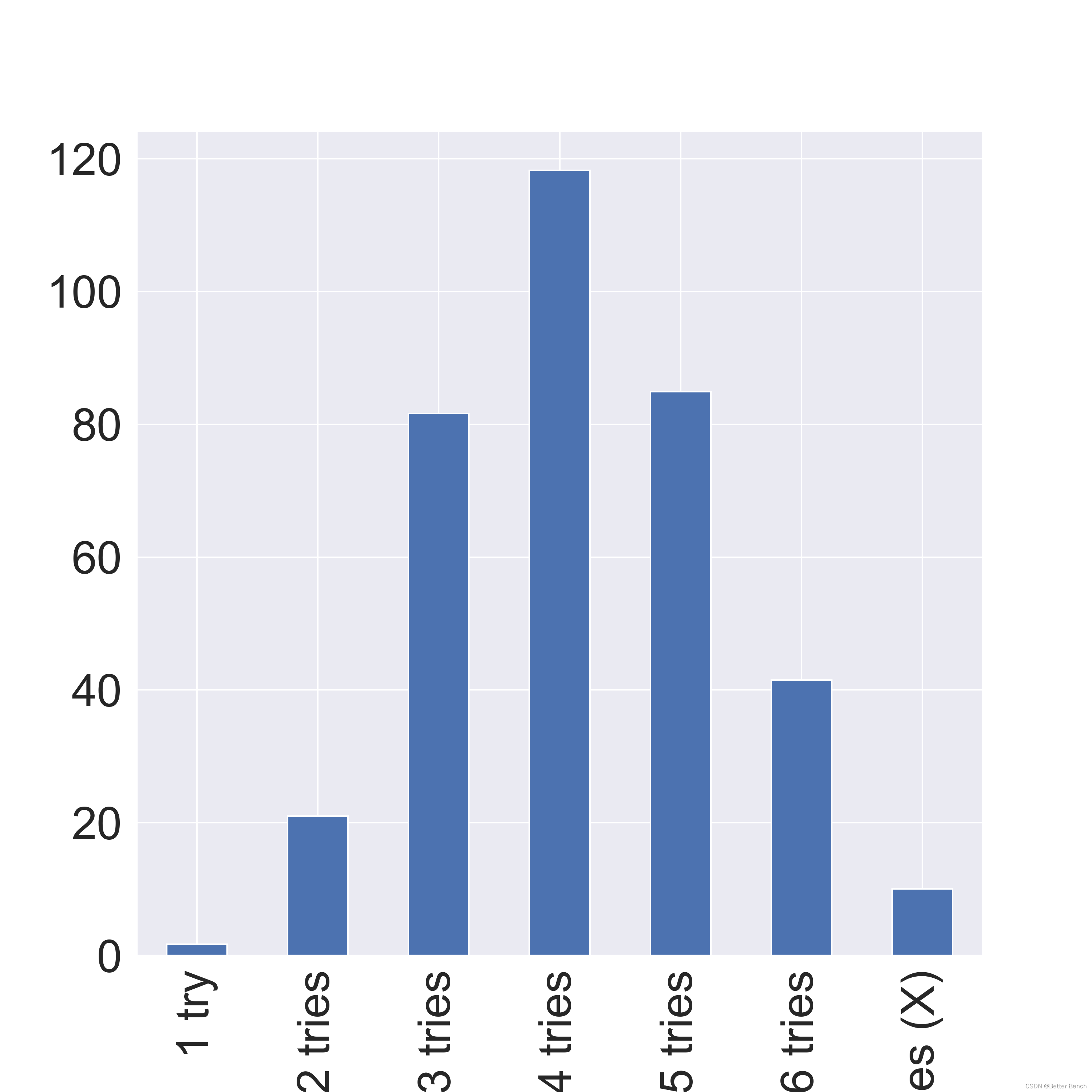
2023年美赛C题Wordle预测问题三、四建模及Python代码详细讲解
更新时间:2023-2-19 16:30 相关链接 （1）2023年美赛C题Wordle预测问题一建模及Python代码详细讲解 （2）2023年美赛C题Wordle预测问题二建模及Python代码详细讲解 （3）2023年美赛C题Wordle预测问题三、四建模…...
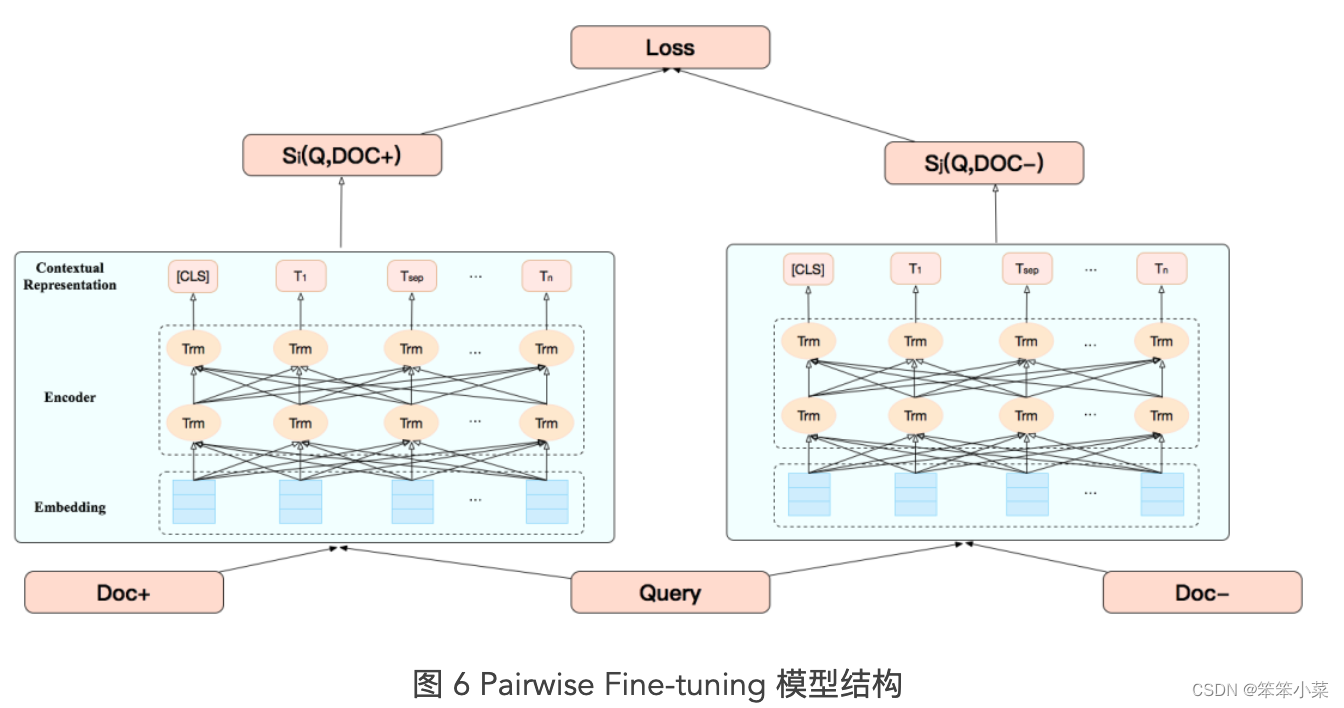
相关性-回忆录（持续更新）
1.TODO方向 （1）数据增强：finetuning阶段需要大量人工标注样本，消耗时间和成本。用户点击数据作为弱监督学习，可以尝试图网络构建节点和边（query聚合）； 使用展现未点击生成对抗网络进…...
(必备技能)使用Python实现屏幕截图
(必备技能)使用Python实现屏幕截图 文章目录 (必备技能)使用Python实现屏幕截图 一、序言二、环境配置 1、下载pyautogui包2、下载opencv-python包3、下载PyQt5包4、下载pypiwin32包 三、屏幕截屏源码与解析 1、使用pyautogui方法实现截屏2、使用PyQt方法实现截屏 a.获取窗口…...
「数据仓库」怎么选择现代数据仓库?
构建自己的数据仓库时要考虑的基本因素我们用过很多数据仓库。当我们的客户问我们，对于他们成长中的公司来说，最好的数据仓库是什么时，我们会根据他们的具体需求来考虑答案。通常，他们需要几乎实时的数据，价格低廉&…...
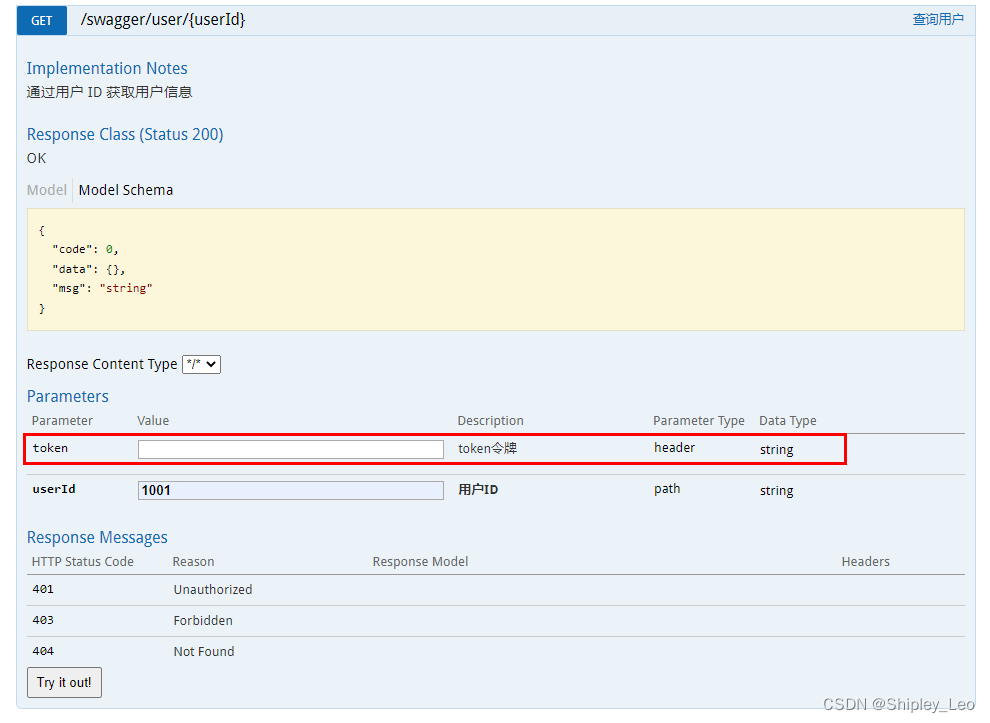
6.3 使用 Swagger 生成 Web API 文档
第6章 构建 RESTful 服务 6.1 RESTful 简介 6.2 构建 RESTful 应用接口 6.3 使用 Swagger 生成 Web API 文档 6.4 实战：实现 Web API 版本控制 6.3 使用 Swagger 生成 Web API 文档 高质量的 API 文档在系统开发的过程中非常重要。本节介绍什么是 Swaggerÿ…...
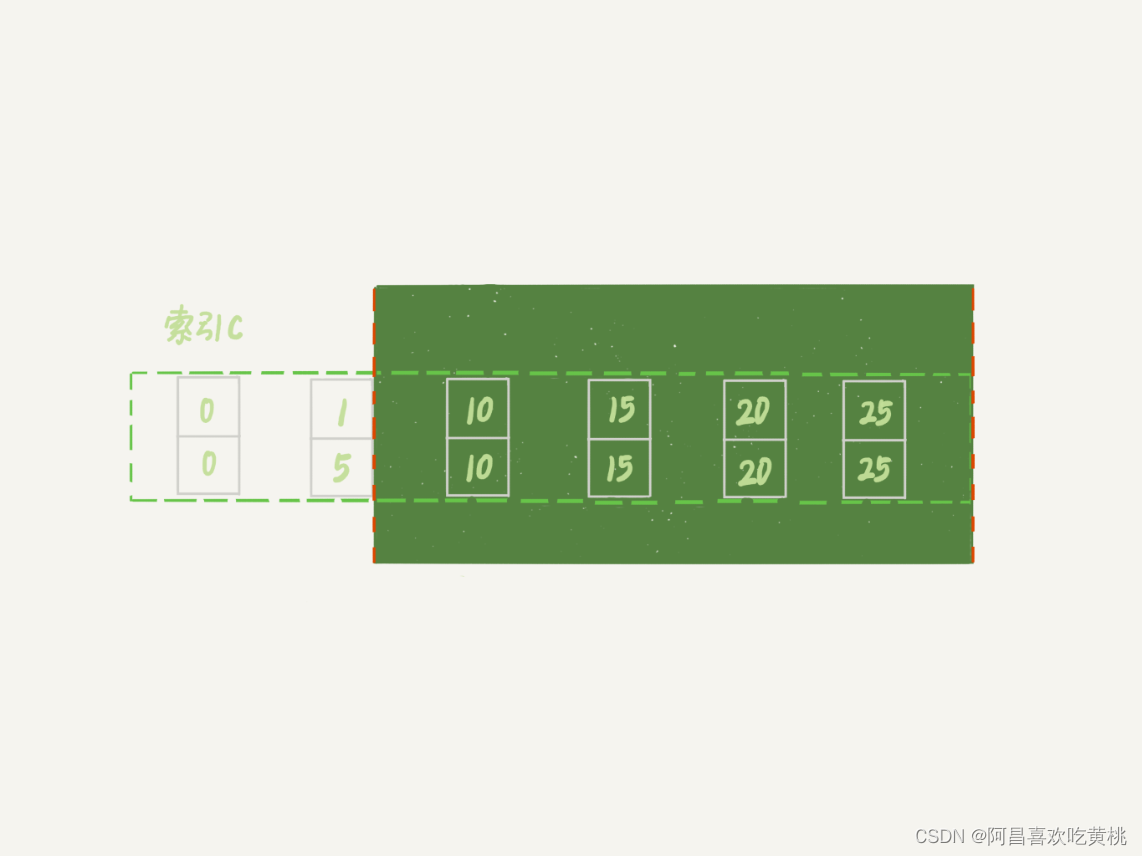
Day894.加锁规则的一些问题 -MySQL实战
加锁规则的一些问题 Hi，我是阿昌，今天学习记录的是关于加锁规则的一些问题的内容。 加锁规则，这个规则中，包含了两个“原则”、两个“优化”和一个“bug”： 原则 1：加锁的基本单位是 next-key lock。nex…...
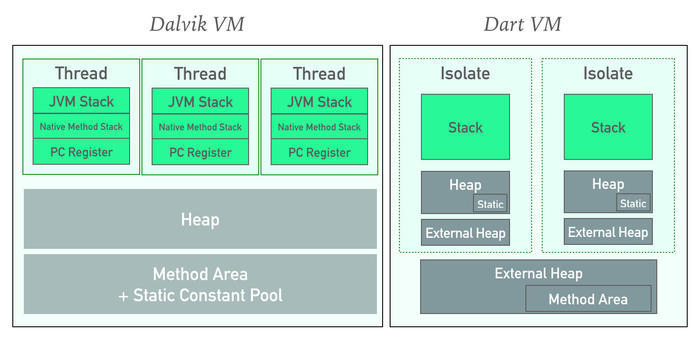
【Flutter入门到进阶】Dart进阶篇---Dart异步编程
1 并行与并发的编程区别 1.1 并发与并行 1.1.1 说明 我们举个例子,如果有条高速公路 A 上面并排有 8 条车道,那么最大的并行车辆就是 8 辆此条高速公路 A 同时并排行走的车辆小于等于 8 辆的时候,车辆就可以并行运行。 CPU 也是这个原理,一个 CPU 相当于一个高速公路 A,核心数…...
点云配准方法原理（NDT、ICP）
配准是点云处理中的一个基础问题，众多学者此问题进行了广泛而深入的研究，也出现了一系列优秀成熟的算法，在三维建模、自动驾驶等领域发挥着重要的作用。 本文主要介绍粗配准NDT (Normal Distribution Transform) 与 精配准ICP (Iterative Cl…...
大规模 IoT 边缘容器集群管理的几种架构-0-边缘容器及架构简介
📚️Reference: IoT 边缘计算系列文章 什么是边缘容器？ 边缘容器的概念 边缘容器是分散的计算资源，尽可能靠近最终用户或设备，以减少延迟、节省带宽并增强整体数字体验。 可以访问互联网的设备数量每天都在增加。有包括但不限于…...
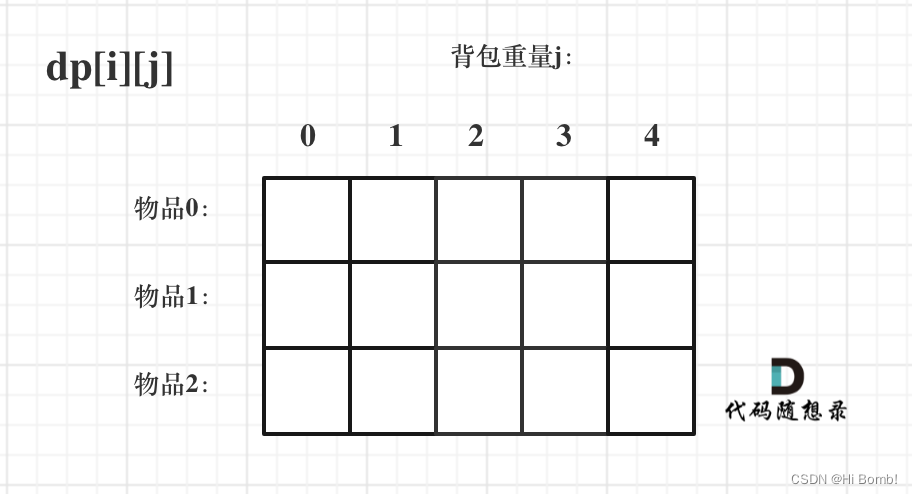
代码随想录算法训练营第45天动态规划 背包基础 1 2、 416. 分割等和子集
文章目录01背包基础 （二维数组）思路递推公式初始化遍历顺序一维dp数组（滚动数组）一维数组的递推公式遍历顺序LeetCode 416. 分割等和子集思路总结01背包基础 （二维数组） 思路 根据动态规划五部进行分析&a…...
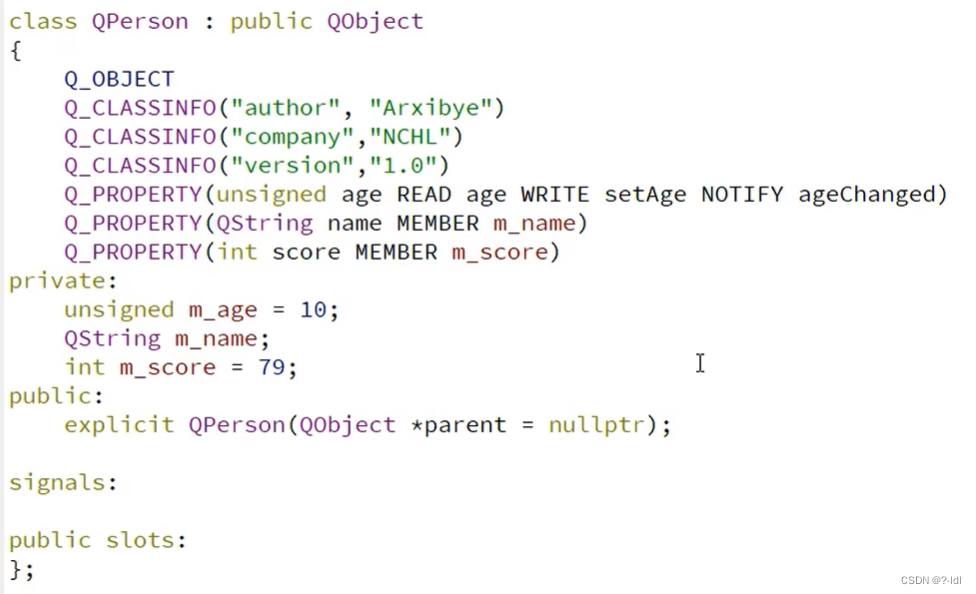
QT学习记录(六）类对象属性
类对象属性用来描述类对象的一些信息和当前的状态。类对象属性可以由类的编写者在编写类的时候定义，也可以由类的使用者在使用对象的时候定义。 由类的编写者定义 QPROPERTY()宏就是用来定义一个对象属性。 以第二行属性举例 QPROPERTY(bool enabled READ isEnabl…...
Spring Cloud Alibaba从搭建到源码完整进阶教程
微服务简介 Spring Cloud Alibaba 微服务简介 Nacos注册中心配置中心 Spring Cloud Nacos实战（一）- 下载和安装 Spring Cloud Nacos实战（二）- 服务提供者注册 Spring Cloud Nacos实战（三）- 服务消费者…...
Spring Cloud Nacos实战（一）- 下载和安装
Spring Cloud Alibaba Nacos下载和安装 Nacos介绍 Nacos（Naming Configuration Service） 是一个易于使用的动态服务发现、配置和服务管理平台，用于构建云原生应用程序 服务发现是微服务架构中的关键组件之一。Nacos 致力于帮助您发现…...
深入理解设备像素比
文章目录参考描述像素分辨率显示分辨率图像分辨率物理分辨率分辨率单位（仅部分）DPIPPI设备像素比设备物理像素设备独立像素设备像素比产生放大与缩小尾声参考 项目描述关于物理像素、逻辑像素（css像素）、分辨率、像素比的超详细讲…...
Revisiting Distributed Synchronous SGD 带有Back-up机制的分布式同步SGD方法 论文精读
论文链接：Revisiting Distributed Synchronous SGD ABS 本文介绍了用于分布式机器学习的同步和异步SGDSGDSGD，同时指出各自的缺点：stragglersstragglersstragglers和stalenessstalenessstaleness。 同时为了解决同步SGDSGDSGD存在straggle…...
shiro CVE-2020-13933
0x00 前言 同CVE-2020-1957，补充一下笔记，在CVE-2020-1957的基础上进行了绕过。 影响版本：Apache Shiro < 1.6.0 环境搭建参考：shiro CVE-2020-1957 0x01 漏洞复现 CVE-2020-13933中使用%3b绕过了shiro /*的检测方式&…...
斐波那契数列(递归+迭代)
目录什么是斐波那契数列递归写法使用递归写法的缺点迭代写法(效率高)什么是斐波那契数列 斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多斐波那契（Leonardo Fibonacci）以兔子繁殖为例…...
2022黑马Redis跟学笔记.实战篇(六)
2022黑马Redis跟学笔记.实战篇 六4.7.达人探店功能4.7.1.分享探店图文1. 达人探店-发布探店笔记2. 达人探店-查看探店笔记4.7.2.点赞功能4.7.3.基于List实现点赞用户列表TOP104.7.4.基于SortedSet实现点赞排行榜4.8.关注列表4.8.1.关注列表实现原理4.8.2.添加关注1. 好友关注-关…...
Linux-VMware常用设置(时间+网络)及网络连接激活失败解决方法-基础篇②
目录一、设置时间二、网络设置1. 激活网卡方法一：直接启动网卡（仅限当此）方法二：修改配置文件（永久）2. 将NAT模式改为桥接模式什么是是NAT模式？如何改为桥接模式？三、虚拟机网络连接…...
vue3学习总结1
一.vue3与vue2相比带来哪些变化？a.性能的提升（包括打包大小减少，初次渲染的速度加快，更新渲染速度加快，内存减少）b.源码的升级（响应式的原理发生了变化，由原来的defineProperty变成了…...
SpringBoot统一功能处理
一、统一用户登录权限验证 1.1Spring拦截器 实现拦截器需要以下两步： 1.创建自定义拦截器，实现 HandlerInterceptor 接⼝的 preHandle（执行具体方法之前的预处理）方法。 2.将⾃定义拦截器加⼊ WebMvcConfigurer 的 addIntercept…...
2022年3月电子学会Python等级考试试卷（五级）答案解析
目录 一、单选题(共25题，共50分) 二、判断题(共10题，共20分) 三、编程题(共3题，共30分) 青少年软件编程（Python）等级考试试卷（五级&#...
【C++】智能指针
目录 一、先来看一下什么是智能指针 二、 auto_ptr 1、C98版本 2、C11的auto_ptr 三、boost 库中的智能指针 1. scoped_ptr 2、shared_ptr（最好的智能指针） 四、C11中新提供的智能指针 unique_ptr shared_ptr std::shared_ptr的循环引用问题…...