ElementUI 树形表格的使用以及表单嵌套树形表格的校验问题等汇总
目录
一、树形表格如何添加序号体现层级关系
二、树形表格展开收缩图标位置放置,设置指定列
三、表单嵌套树形表格的校验问题以及如何给校验rules传参
普通表格绑定如下:这种方法只能校验表格的第一层,树形需要递归设置子级节点prop。
树形表格绑定如下:使用下面的方法(复制粘贴可以直接用)
四、树形表格如何通过某属性值进行过滤展示
1、可使用:row-style="tableRowClassName"去进行筛选 控制显隐 这个方法比较简单且不改变原treedata数据
2、过滤满足属性值需要的节点生成新的treedata数据来渲染表格
一、树形表格如何添加序号体现层级关系
实现:treeData为表格数据,递归调用getProjectIndex方法即可实现;例如:1,1,1,1.2
<el-table-column label="序号" width="100" type=""><template slot-scope="scope">{{ scope.row.projectIndex }}</template>
</el-table-column>// 添加索引addIndex() {this.treeData.forEach((node, i) => {this.getProjectIndex(node, '', i)// 默认展开第一层this.expandKeys.push(node.id + '')})},// 获取序号getProjectIndex(node, parentIndex, index) {const projectIndex = parentIndex ? `${parentIndex}.${index + 1}` : `${index + 1}`node.projectIndex = projectIndexif (node.children) {node.children.forEach((child, i) => {this.getProjectIndex(child, projectIndex, i)})}},二、树形表格展开收缩图标位置放置,设置指定列
在不需要的列前加上 type=""
<el-table-column label="序号" width="100" type=""><template slot-scope="scope">{{ scope.row.projectIndex }}</template>
</el-table-column>三、表单嵌套树形表格的校验问题以及如何给校验rules传参
需求:一个树形表格中每个树节点都需要有日期范围,想要校验子节点的日期范围不能超过父节点;
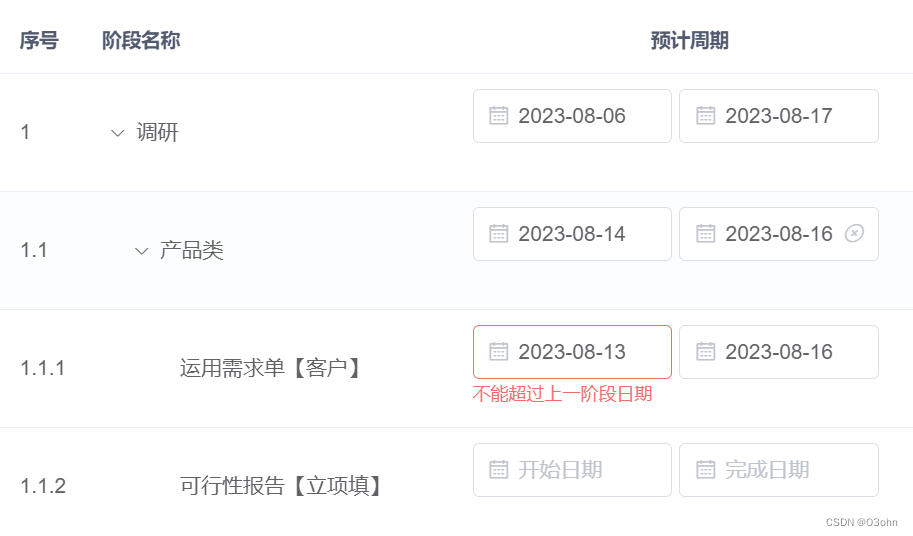
解决:如何绑定form的prop值?先了解如何绑定普通表格进行校验
-
普通表格绑定如下:这种方法只能校验表格的第一层,树形需要递归设置子级节点prop。
<template slot-scope="scope"><el-form-item :prop="`treeData.${scope.$index}.beginDate`" :rules="beginDateRules"><el-date-pickerv-model="scope.row.beginDate"type="date"clearableformat="yyyy-MM-dd"value-format="yyyy-MM-dd"placeholder="开始日期"/></el-form-item> </template> -
树形表格绑定如下:使用下面的方法(复制粘贴可以直接用)
findPosi(tree, targetId, path = '') {for (let i = 0; i < tree.length; i++) {const node = tree[i]if (node.id === targetId) {return path + i}if (node.children && node.children.length > 0) {const childPath = `${path}${i}.children.`const result = this.findPosi(node.children, targetId, childPath)if (result !== null) {return result}}}return null}具体代码实现如下:
//1、表单表格嵌套实现代码 其余省略
<el-form ref="treeForm" :model="treeForm"><el-table:data="treeForm.treeData"row-key="id":row-style="tableRowClassName":expand-row-keys="expandKeys":tree-props="{ children: 'children'}"><el-table-column label="预计周期" width="310" align="center"><template slot-scope="scope"><el-form-item:prop="'treeData.' + findPosi(treeForm.treeData,scope.row.id) + '.beginDate'":rules="beginDateRules(scope.row)"><el-date-pickerv-model="scope.row.beginDate":style="{width: '100%'}"type="date"clearableformat="yyyy-MM-dd"value-format="yyyy-MM-dd"placeholder="开始日期"/></el-form-item></template></el-table-column></el-table></el-form>//2、script标签内容
//定义的数据格式
treeForm: {treeData: []
},
//方法调用 给rules传参方式
beginDateRules(row) {return [{ validator: (rule, value, callback) => { this.validateBeginDate(rule, value, callback, row) }, trigger: 'blur' }]},
validateBeginDate(rule, value, callback, row) {// 没有父节点不做判断if (row.parentId === 0) {callback()} else {// 查找父节点const node = findParentId(this.treeForm.treeData, row.parentId)if (value && node.beginDate !== null) {if (new Date(value) < new Date(node.beginDate)) {callback(new Error('不能超过上一阶段日期'))} else {callback()}} else {callback()}}},
//用到的工具类
// 1定义一个递归函数,接受一个对象或数组,一个目标id值和一个路径数组作为参数 查找目标id所在的路径findPosi(tree, targetId, path = '') {for (let i = 0; i < tree.length; i++) {const node = tree[i]if (node.id === targetId) {return path + i}if (node.children && node.children.length > 0) {const childPath = `${path}${i}.children.`const result = this.findPosi(node.children, targetId, childPath)if (result !== null) {return result}}}return null}
//2通过节点id查找其父节点信息
/*** @param {*} tree* @param {*} targetId* @param {*} parentId* @returns* 通过节点id查找其父节点信息*/
export function findParentId(tree, targetId) {for (const node of tree) {if (node.id === targetId) {return node}if (node.children) {const result = findParentId(node.children, targetId, node.id)if (result !== null) {return result}}}return null
}
四、树形表格如何通过某属性值进行过滤展示
1、可使用:row-style="tableRowClassName"去进行筛选 控制显隐 这个方法比较简单且不改变原treedata数据
tableRowClassName(data) {if (data.row.enabled === '0') {return { display: 'none' }}},2、过滤满足属性值需要的节点生成新的treedata数据来渲染表格
原数据 treeData:[] 新数据:tree:[] 调用getenabledNodes()方法
// 筛选选中节点getenabledNodes() {const tree = this.filterUnenabledNodes(this.treeData)console.log(tree)},filterUnenabledNodes(treeData) {const filteredData = []treeData.forEach(node => {if (node.enabled === '1') {filteredData.push(Object.assign({}, node, {children: node.children ? this.filterUnenabledNodes(node.children) : []}))}})return filteredData},相关文章:

ElementUI 树形表格的使用以及表单嵌套树形表格的校验问题等汇总
目录 一、树形表格如何添加序号体现层级关系 二、树形表格展开收缩图标位置放置,设置指定列 三、表单嵌套树形表格的校验问题以及如何给校验rules传参 普通表格绑定如下:这种方法只能校验表格的第一层,树形需要递归设置子级节点prop。 树…...

解决“Unable to start embedded Tomcat“错误的完整指南
系列文章目录 文章目录 系列文章目录前言一、查看错误信息二、确认端口是否被占用三、检查依赖版本兼容性四、清理临时文件夹五、检查应用程序配置六、检查依赖冲突七、查看异常堆栈信息八、升级或降级Spring Boot版本总结前言 在使用Spring Boot开发应用程序时,有时可能会遇…...
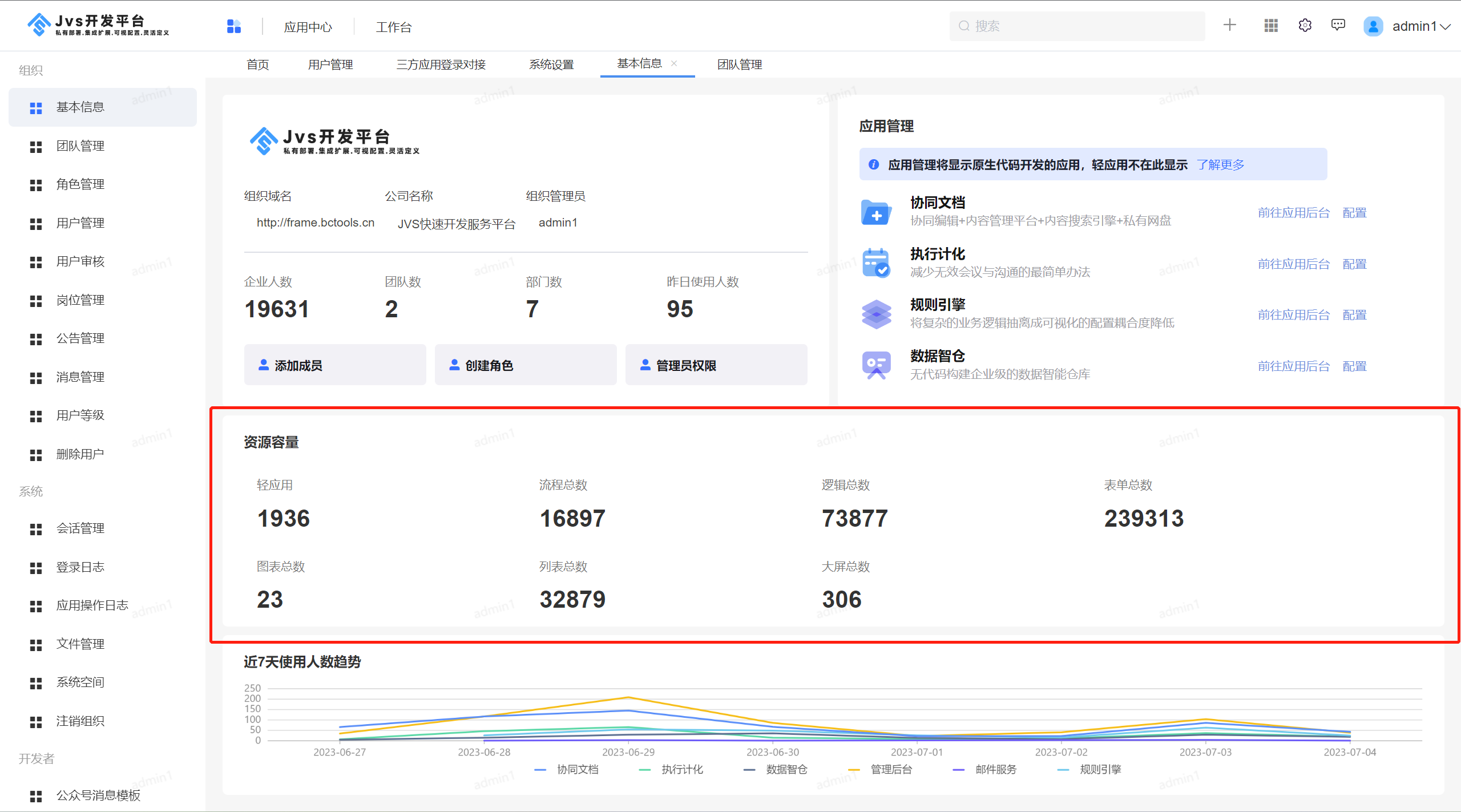
JVS开源基础框架:平台基本信息介绍
JVS是面向软件开发团队可以快速实现应用的基础开发脚手架,主要定位于企业信息化通用底座,采用微服务分布式框架,提供丰富的基础功能,集成众多业务引擎,它灵活性强,界面化配置对开发者友好,底层容…...

C++ - max_element
在C中,要找到一个数组中的最大元素,可以使用 std::max_element 函数。以下是使用步骤: 包含 <algorithm> 头文件,这里定义了 std::max_element 函数。声明一个数组,并初始化它。使用 std::max_element 函数来查找…...

聚隆转债上市价格预测
聚隆转债 基本信息 转债名称:聚隆转债,评级:A,发行规模:2.185亿元。 正股名称:南京聚隆,今日收盘价:16.64元,转股价格:18.27元。 当前转股价值 转债面值 / 转…...
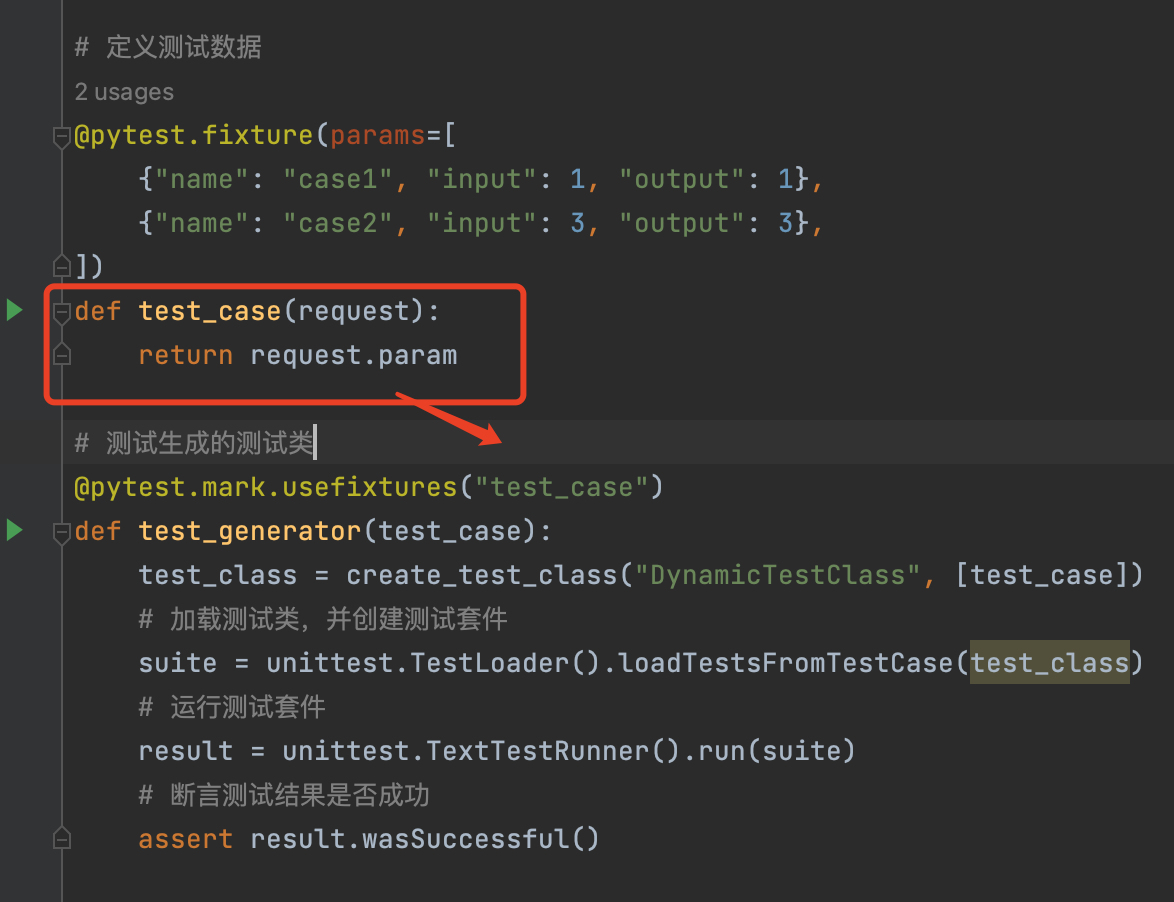
pytest自动生成测试类 demo
一、 pytest自动生成测试类 demo # -*- coding:utf-8 -*- # Author: 喵酱 # time: 2023 - 08 -15 # File: test4.py # desc: import pytest import unittest# 动态生成测试类def create_test_class(class_name:str, test_cases:list) -> type:"""生成测试类…...

服务器卡顿了该如何处理
服务器卡顿了该如何处理 当Windows系统的服务器出现卡顿问题时,以下是一些常见的故障排除步骤: 1.检查网络连接:确保服务器的网络连接正常。检查网络设备、交换机、防火墙等设备,确保它们正常运行。尝试通过其他计算机访问服务器…...

常量对象 只能调用 常成员函数
一、遇到问题: //函数声明 void ReadRanFile(CString szFilePath); const CFvArray<CString>& GetPanelGrade() const { return m_fvArrayPanelGrade; } //在另一个文件中调用ReadtRanFile这个函数 const CFsJudConfig& psJudConfig m_pFsDefJu…...

Progressive-Hint Prompting Improves Reasoning in Large Language Models
本文是LLM系列的文章,针对《Progressive-Hint Prompting Improves Reasoning in Large Language Models》的翻译。 渐进提示改进了大型语言模型中的推理 摘要1 引言2 相关工作3 渐进提示Prompting4 实验5 结论6 实现细节7 不足与未来工作8 广泛的影响9 具有不同提示…...

mysql中INSERT INTO ... ON DUPLICATE KEY UPDATE的用法,以及与REPLACE INTO 语句用法的异同
INSERT INTO ... ON DUPLICATE KEY UPDATE 是 MySQL 中一种用于插入数据并处理重复键冲突的语法。与之相似的还有 REPLACE INTO 语句。以下是它们的用法和异同点的详细说明: 一、INSERT INTO ... ON DUPLICATE KEY UPDATE INSERT INTO ... ON DUPLICATE KEY UPDAT…...
)
wireshark 实用过滤表达式(针对ip、协议、端口、长度和内容)
wireshark 实用过滤表达式(针对ip、协议、端口、长度和内容) 1. 关键字 “与”:“eq” 和 “”等同,可以使用 “and” 表示并且, “或”:“or”表示或者。 “非”:“!" 和 "not”…...
MATLAB图形窗口固定
起因是上次作图的时候写了: clc clear close all 这三个典型的刷新语句 清空工作区、命令行并且关闭图窗 就导致每次我把图窗拉到合适的位置观察,再一次点击运行都会重新刷新在出生点(x) 所以想把图窗固定在某个位置 显然更…...

【数据结构】_7.二叉树概念与基本操作
目录 1.树形结构 1.1 树的概念 1.2 树的相关概念 1.3 树的表示 1.4 树在实际中的应用—表示文件系统的目录树结构 编辑2.二叉树 2.1 概念 2.2 特殊二叉树 2.3 二叉树的性质 2.4 二叉树的存储结构 2.4.1 顺序存储结构(数组存储结构) 2.4.2…...
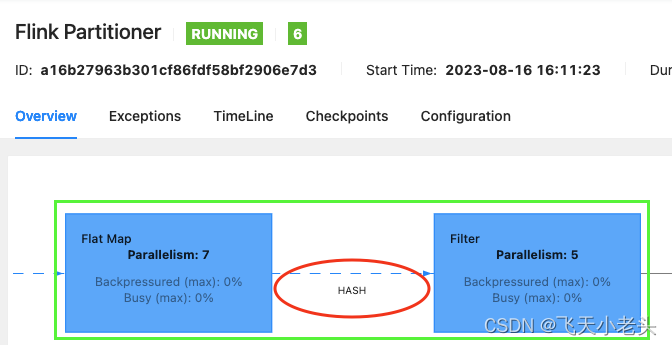
Flink之Partitioner(分区规则)
Flink之Partitioner(分区规则) 方法注释global()全部发往1个taskbroadcast()广播(前面的文章讲解过,这里不做阐述)forward()上下游并行度一致时一对一发送,和同一个算子连中算子的OneToOne是一回事shuffle()随机分配(只是随机,同Spark的shuffle不同)rebalance()轮询分配,默认机…...
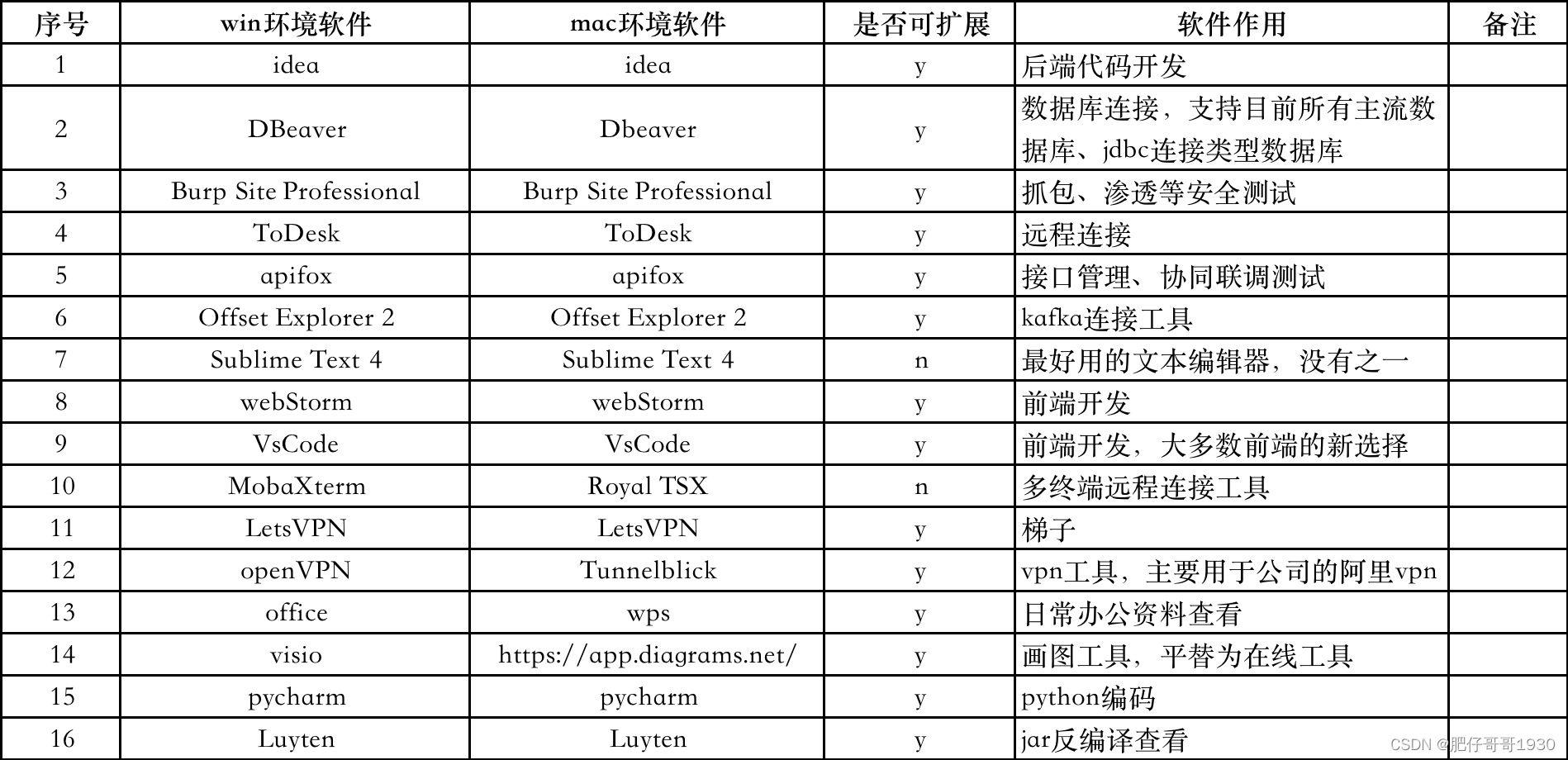
tk切换到mac的code分享
文章目录 前言一、基础环境配置二、开发软件与扩展1.用到的开发软件与平替、扩展情况 总结 前言 最近换上了coding人生的第一台mac,以前一直偏好tk,近来身边的朋友越来越多的用mac了,win的自动更新越来越占磁盘了,而且win11抛弃了…...
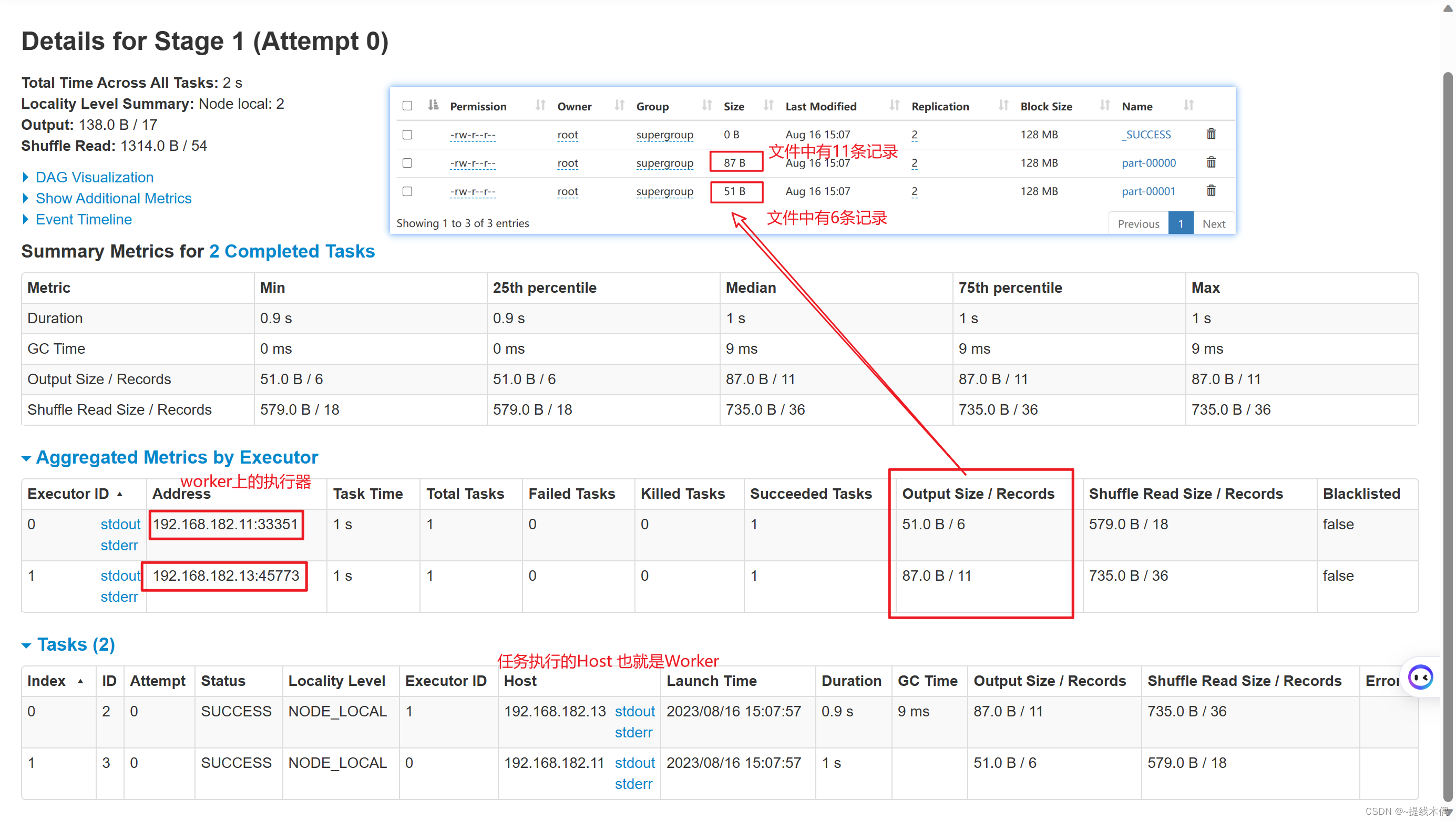
spark的standalone 分布式搭建
一、环境准备 集群环境hadoop11,hadoop12 ,hadoop13 安装 zookeeper 和 HDFS 1、启动zookeeper -- 启动zookeeper(11,12,13都需要启动) xcall.sh zkServer.sh start -- 或者 zk.sh start -- xcall.sh 和zk.sh都是自己写的脚本-- 查看进程 jps -- 有…...
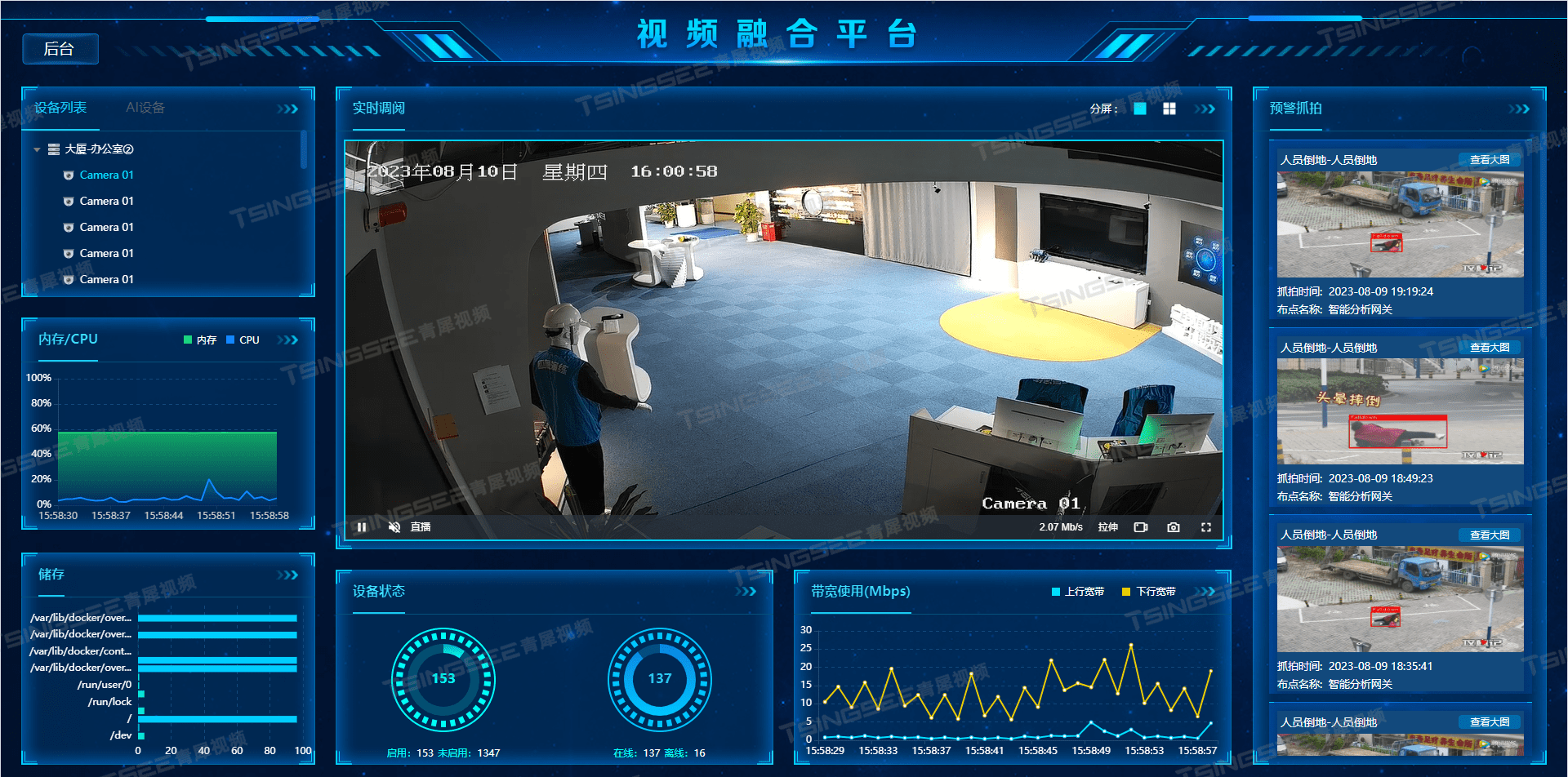
浅析基于视频汇聚与AI智能分析的新零售方案设计
一、行业背景 近年来,随着新零售概念的提出,国内外各大企业纷纷布局智慧零售领域。从无人便利店、智能售货机,到线上线下融合的电商平台,再到通过大数据分析实现精准推送的个性化营销,智慧零售的触角已经深入各个零售…...
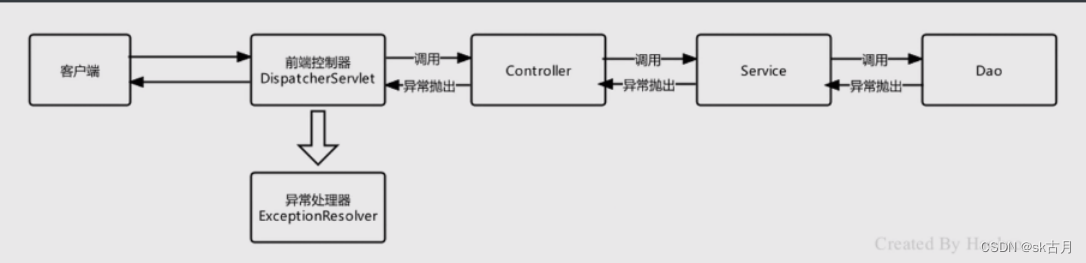
SpringMVC之异常处理
SpringMVC之异常处理 异常分为编译时异常和运行时异常,编译时异常我们trycatch捕获,捕获后自行处理,而运行时异常是不可预期的,就需要规范编码来避免,在SpringMVC中,不管是编译异常还是运行时异常ÿ…...

保险龙头科技进化论:太保的六年
如果从2013年中国首家互联网保险公司——众安在线的成立算起,保险科技在我国的发展已走进第十个年头。十年以来,在政策指引、技术发展和金融机构数字化转型的大背景下,科技赋能保险业高质量发展转型已成为行业共识。 大数据、云计算、人工智…...

升级STM32电机PID速度闭环编程:从F1到F4的移植技巧与实例解析
引言: 在嵌入式系统开发中,STM32系列微控制器广泛应用于各种应用领域。而对于直流有刷电机的控制,PID速度闭环是一种常用的控制方式。本文将以此为例,探讨如何从STM32F1系列移植到STM32F4系列,并详细介绍HAL库在不同型…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
