力扣75——图深度优先搜索
总结leetcode75中的图深度优先搜索算法题解题思路。
上一篇:力扣75——二叉搜索树
力扣75——图深度优先搜索
- 1 钥匙和房间
- 2 省份数量
- 3 重新规划路线
- 4 除法求值
- 1-4 解题总结
1 钥匙和房间
题目:
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。
你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,
即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入
所有 房间返回 true,否则返回 false。
题解:
我的方法:广度优先搜索。进入一个房间t,拿到里面的钥匙tmp,然后把钥匙tmp压入队列q中。while循环从队列q拿钥匙,直到q空了为止。最后检查所有房间visit是否都被访问。
官方代码:深度优先搜索。利用递归函数dfs:进入一个房间,拿到钥匙,再用for循环调用dfs函数。
class Solution {
public:bool canVisitAllRooms(vector<vector<int>>& rooms) {int numRooms = rooms.size();vector<int> visit(numRooms,0);visit[0] = 1;vector<int> tmp;queue<int> q;q.push(0);while (!q.empty()) {tmp = rooms[q.front()];q.pop();if (!tmp.empty()) {for (int t : tmp) {if (visit[t] == 1)continue;q.push(t);visit[t] = 1;}}}for (int v : visit) {if (v == 0) return false;}return true;}
};
//官方的代码更简洁合理
/*
class Solution {
public:vector<int> vis;int num;void dfs(vector<vector<int>>& rooms, int x) {vis[x] = true;num++;for (auto& it : rooms[x]) {if (!vis[it]) {dfs(rooms, it);}}}bool canVisitAllRooms(vector<vector<int>>& rooms) {int n = rooms.size();num = 0;vis.resize(n);dfs(rooms, 0);return num == n;}
};
*/
2 省份数量
题目:
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,
且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和
第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。返回矩阵中 省份 的数量。
题解:
深度优先搜索。for遍历每个城市,用递归函数dfs找到所有与当前城市i直接或间接相连的城市,用visit来标记已经搜索过的城市。
class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {int nums = 0, nC = isConnected.size();vector<int> visit(nC, 0);for (int i = 0; i < nC; i++) {if (visit[i] == 0) {nums++;dfs(isConnected, visit, i);}}return nums;}void dfs(vector<vector<int>>& isConnected,vector<int> & visit,int i) {visit[i] = 1;for (int j = 0; j < isConnected.size(); j++) {if (isConnected[i][j] == 1&& visit[j] == 0) {dfs(isConnected, visit, j);}}}
};
3 重新规划路线
题目:
n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有
唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通
拥堵的状况。路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向
路线。今年,城市 0 将会举办一场大型比赛,很多游客都想前往城市 0 。
请你帮助重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
题解:
广度优先搜索。目的是将所有路线的方向都朝着城市0,所以遍历所有与城市0直接相连的城市,然后对这每一个相连的城市进行广度优先搜索,更改那些方向错误的路线。具体的过程在代码中有注释。
class Solution {
public:int minReorder(int n, vector<vector<int>>& connections) {vector<vector<int>> conn_idx(n, vector<int>());//这里使用了类似于邻接表的方法,将和节点有关的连接的id序号加入到对应的向量中//这样在后面遍历的时候,只要查找connections里面对应的id即可//要注意这里连接两端都加入了连接的序号for (int i = 0; i < connections.size(); i++) {conn_idx[connections[i][0]].push_back(i);conn_idx[connections[i][1]].push_back(i);}vector<bool> vi(connections.size(), false);//此处标志的是某条边是否被访问过,而不是某个点是否被访问过int ans = 0;queue<int> que;que.push(0);while (!que.empty()) {auto q = que.front();que.pop();//这个循环是对和节点q相关的连接进行遍历,通过上面存储的连接的id进行遍历for (auto idx : conn_idx[q]) {if (vi[idx]) continue;vi[idx] = true;int a = connections[idx][0];//连接的起始int b = connections[idx][1];//连接的终点ans += (a == q);//如果当前点是出的,那么要修改为入,ans++a = (a == q) ? b : a;que.push(a);}}return ans;}
};
4 除法求值
题目:
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i]
= [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示
单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根
据已知条件找出 Cj / Dj = ? 的结果作为答案。返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现
了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。注意:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
注意:未在等式列表中出现的变量是未定义的,因此无法确定它们的答案。
题解:
并查集。
1 先定义1个unordered_map类型的parent,它记录了一个数的被除数,被除数的被除数是它自己。
2 再定义1个unordered_map类型的mp,记录1个数除被除数得到的值。
3 接着定义函数find(),该函数可以找到一个数的祖先。在这个过程中,如果发现一个数的祖先跟它隔了2代或更多代,就递归进行压缩,并修改对应的mp值。
4 然后,通过for循环遍历equations,将所以除法公式及其结果记录好。
5 最后,计算queries中的问题。如果被除数或除数不存在于parent中,则无法求解;如果除数和被除数的祖先不是同一个,也无法求解;如果除数和被除数是同一个祖先,则直接用它们的mp值做除法即可。
class Solution {
public:unordered_map<string, string> parent;unordered_map<string, double> mp;string find(string x){if(parent[x] == x) return x;string px = parent[x];string res = parent[x] = find(parent[x]); mp[x] *= mp[px];return res;}vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {int n = equations.size();for(int i = 0; i < n; i ++ ){string a = equations[i][0], b = equations[i][1];double v = values[i];if(parent.find(a) == parent.end() && parent.find(b) == parent.end()){parent[a] = a; parent[b] = a;mp[b] = v, mp[a] = 1.0;}else if(parent.find(a) == parent.end()){parent[a] = a; string pb = find(b);mp[a] = 1.0;mp[pb] = v / mp[b];parent[pb] = a;}else if(parent.find(b) == parent.end()){parent[b] = a;mp[b] = v;}else{string pa = find(a), pb = find(b);if(pa == pb) continue;parent[pb] = pa;mp[pb] = mp[a] * v / mp[b];} }vector<double> res;for(auto &item : queries){string a = item[0], b = item[1];if(parent.find(a) == parent.end() || parent.find(b) == parent.end()) res.push_back(-1.0);else{string pa = find(a), pb = find(b);if(pa != pb) res.push_back(-1.0);else res.push_back(mp[b] / mp[a]);}}return res;}
};
1-4 解题总结
a 题目类型总结:
- 题目1:从1个节点出发,是否可以到达所有节点。
- 题目2:所有节点构成几个连通域。
- 题目3:从任意节点出发,是否可以到达某个节点。
- 题目4:节点1是否可以到达节点2。
b 题目1和题目3本质上是一样的,只是边的方向相反了而已。他们既可以使用深度优先搜索,也可以使用广度优先搜索。
c 题目2既可以使用深度优先搜索,也可以使用广度优先搜索。
d 题目4是检查两个点之间是否连通,所以,用深度优先搜索更合适。
e 这些题目不限制是否会重复经过某个节点,只考虑哪些节点是相通的。
相关文章:

力扣75——图深度优先搜索
总结leetcode75中的图深度优先搜索算法题解题思路。 上一篇:力扣75——二叉搜索树 力扣75——图深度优先搜索 1 钥匙和房间2 省份数量3 重新规划路线4 除法求值1-4 解题总结 1 钥匙和房间 题目: 有 n 个房间,房间按从 0 到 n - 1 编号。最初…...
小程序前台Boot后台校园卡资金管理系统java web学校进销存食堂挂失jsp源代码
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 小程序前台Boot后台校园卡资金管理系统 系统有2权限&…...

数学建模-多元线性回归笔记
数学建模笔记 1.学模型✅ 2.看专题论文并复习算法 多元线性回归 无偏性:预测值与真实值非常接近一致性:样本量无限增大,收敛于待估计参数的真值如何做:控制核心解释变量和u不相关 四类模型回归系数的解释 截距项不用考虑一元线性…...
云安全攻防(十二)之 手动搭建 K8S 环境搭建
手动搭建 K8S 环境搭建 首先前期我们准备好三台 Centos7 机器,配置如下: 主机名IP系统版本k8s-master192.168.41.141Centos7k8s-node1192.168.41.142Centos7k8s-node2192.168.41.143Centos7 前期准备 首先在三台机器上都执行如下的命令 # 关闭防火墙…...

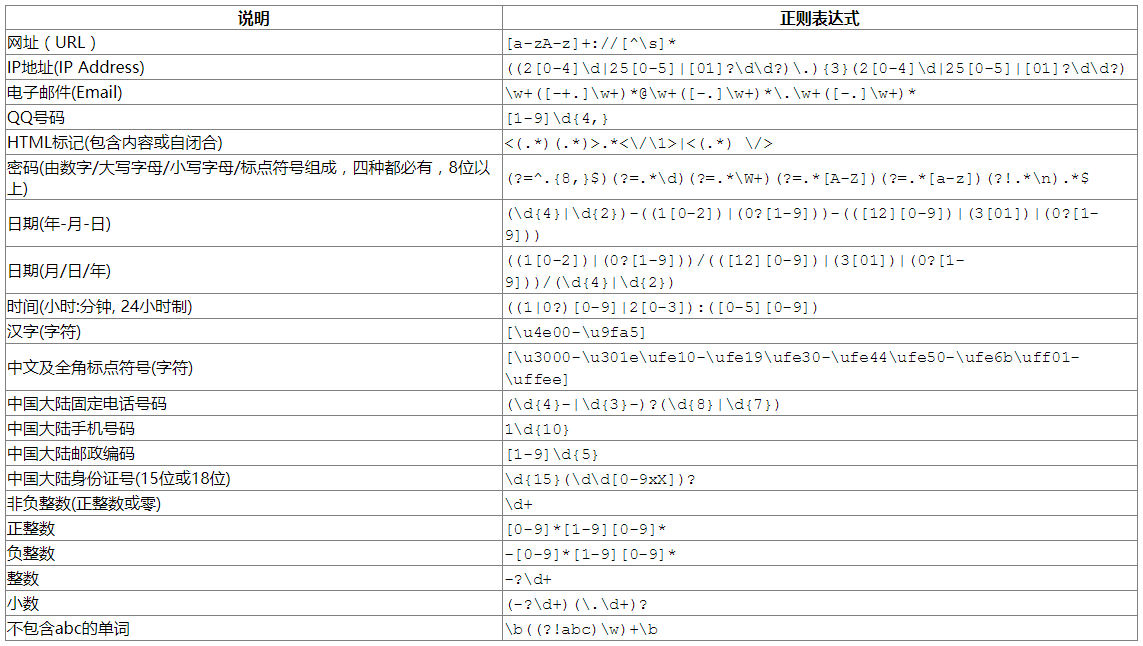
Python学习笔记_基础篇(八)_正则表达式
1. 正则表达式基础 1.1. 简单介绍 正则表达式并不是Python的一部分。正则表达式是用于处理字符串的强大工具,拥有自己独特的语法以及一个独立的处理引擎,效率上可能不如str自带的方法,但功能十分强大。得益于这一点,在提供了正则…...
)
【洛谷 P5736】【深基7.例2】质数筛 题解(判断质数)
【深基7.例2】质数筛 题目描述 输入 n n n 个不大于 1 0 5 10^5 105 的正整数。要求全部储存在数组中,去除掉不是质数的数字,依次输出剩余的质数。 输入格式 第一行输入一个正整数 n n n,表示整数个数。 第二行输入 n n n 个正整数 …...
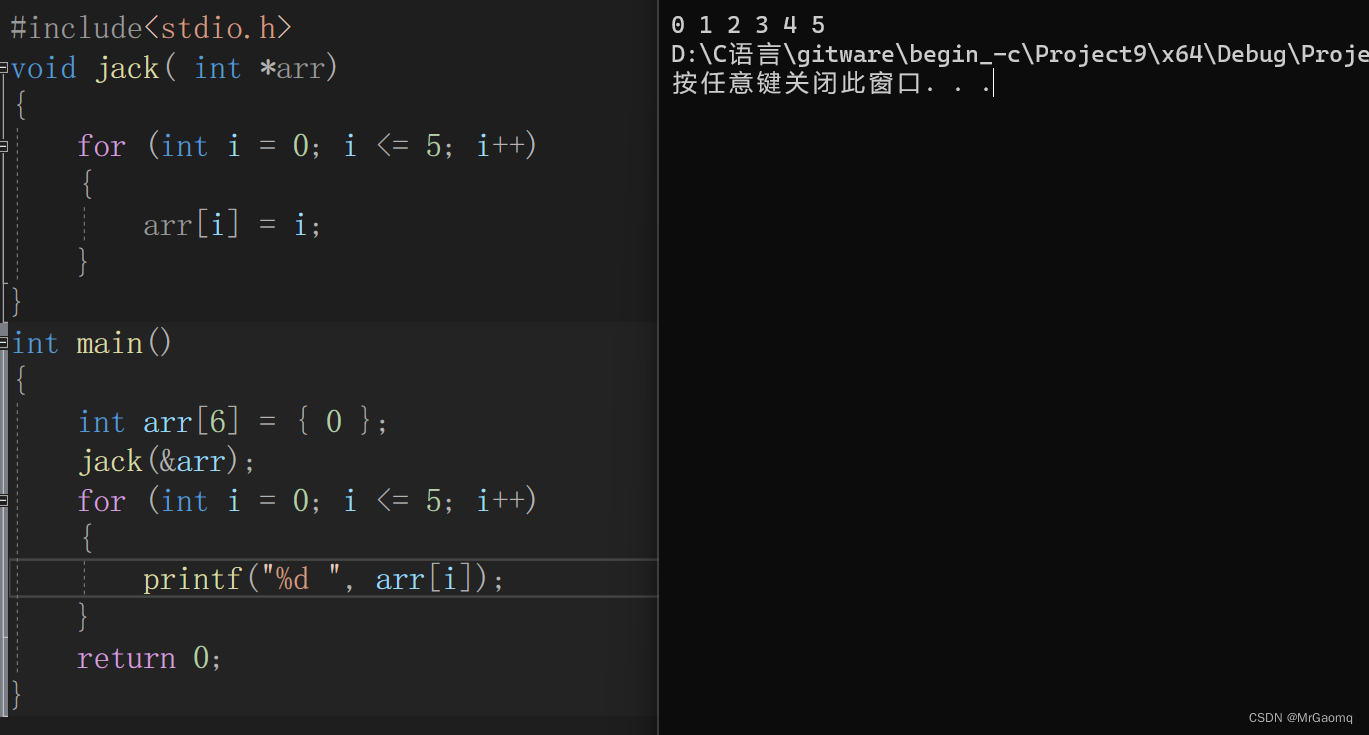
C语言好题解析(一)
目录 选择题1选择题2选择题3选择题4编程题一 选择题1 执行下面程序,正确的输出是( )int x 5, y 7; void swap() {int z;z x;x y;y z; } int main() {int x 3, y 8;swap();printf("%d,%d\n",x, y);return 0; }A: 5,7 B: …...
uniapp微信小程序区分正式版,开发版,体验版
小程序代码区分是正式版,开发版,还是体验版 通常正式和开发环境需要调用不同域名接口,发布时需要手动更换 或者有些东西不想在正式版显示,只在开发版体验版中显示,也需要去手动隐藏 官方没有明确给出判断环境的方法&a…...
更多openEuler镜像加入AWS Marketplace!
自2023年7月openEuler 22.03 LTS SP1正式登陆AWS Marketplace后,openEuler社区一直持续于在AWS上提供更多版本。 目前,openEuler22.03 LTS SP1 ,SP2两个版本及 x86 arm64两种架构的四个镜像均可通过AWS对外提供,且在亚太及欧洲15个Region开放…...
)
【BASH】回顾与知识点梳理(二十四)
【BASH】回顾与知识点梳理 二十四 二十四. 权限规划和身份切换24.1 主机的细部权限规划:ACL 的使用什么是 ACL 与如何支持启动 ACL如何启动 ACL 24.2 ACL 的设定技巧: getfacl, setfaclsetfacl 指令用法介绍及最简单的『 u:账号:权限 』设定getfacl 指令…...
CSRF
CSRF CSRF,跨站域请求伪造,通常攻击者会伪造一个场景(例如一条链接),来诱使用户点击,用户一旦点击,黑客的攻击目的也就达到了,他可以盗用你的身份,以你的名义发送恶意请…...
pyscenic分析:视频教程
我们之前更新过pyscenic的教程:pySCENIC单细胞转录因子分析更新:数据库、软件更新。我们也说过,我们号是放弃R语言版的SCENIC的分析了,因为它比较耗费计算资源和时间,所以我们的单细胞转录因子分析教程都是基于pysceni…...
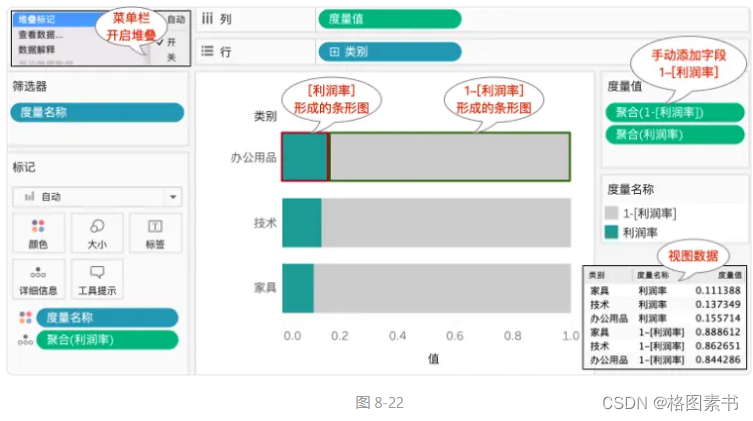
可视化绘图技巧100篇进阶篇(九)-三维百分比堆积条形图(3D Stacked Percentage Bar Chart)
目录 前言 适用场景 绘图工具及代码实现 帆软 实现思路 方案一:使用计算指标 上传数据 添加组件 生成图表 添加计算字段 生成分区柱形图 生成百分比堆积条形图 美化图表 设置标签 设置颜色 效果查看 PC 端 移动端 方案二:使用自助数…...

js实现将文本转PDF格式并下载到本地
html里面需要引入jspdf.umd.min.js和FileSaver.js jspdf.umd.min.js:https://www.npmjs.com/package/jspdf FileSaver.js:https://download.csdn.net/download/weixin_45791806/87272893?spm1001.2014.3001.5503 同时项目的根部目录也需要引入SimHei.tt…...

Servlet+JDBC实战开发书店项目讲解第四篇:登录实现
ServletJDBC 实战开发书店项目讲解第四篇:登录注册实现 在本篇博客中,我们将继续讲解 ServletJDBC 实战开发书店项目。这次我们将重点讲解如何实现登录和注册功能。 1. 创建数据库表 首先,我们需要在数据库中创建两个表,一个用…...

HarmonyOS NEXT新能力,一站式高效开发HarmonyOS应用
2023年8月6日华为开发者大会2023(HDC.Together)圆满收官,伴随着HarmonyOS 4的发布,华为向开发者发布了汇聚所有最新开发能力的HarmonyOS NEXT开发者预览版,并分享了围绕“一次开发,多端部署” “可分可合&a…...
【Java从0到1学习】09 正则表达式
1. 正则表达式概述 在编写处理字符串的程序或网页时,经常会有查找符合某些复杂规则的字符串的需要。正则表达式就是用于描述这些规则的工具。换句话说,正则表达式就是记录文本规则的代码。 正则表达式,又称正规表示法、常规表示法ÿ…...
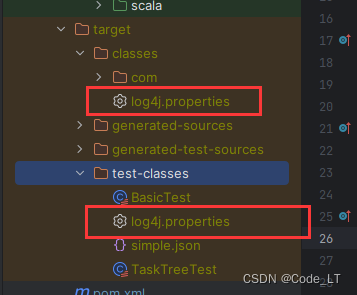
log4j:WARN No appenders could be found for logger问题
本文将idea场景下的使用。 IDEA中,将配置文件命名为log4j.properties(该命名才会被自动加载), 并放到某个目录下(通常放到resources目录),并在resources上右键,找到Mark Directory a…...

【Java】批量生成条形码-itextpdf
批量生成条形码 Controller ApiOperation("商品一览批量生成商品条形码")PostMapping("/batchGenerateProdBarCode")public void batchGenerateProdBarCode(RequestBody ProductListCondition productListCondition,HttpServletResponse response){import…...

SpringBoot登录、退出、获取用户信息的session处理
1、登录方法:login PostMapping("/user/login")public ResponseVo<User> login(Valid RequestBody UserLoginForm userLoginForm,HttpSession session) {ResponseVo<User> userResponseVo userService.login(userLoginForm.getUsername(), …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
