C语言暑假刷题冲刺篇——day2
目录
一、选择题
二、编程题
- 🎈个人主页:库库的里昂
- 🎐CSDN新晋作者
- 🎉欢迎 👍点赞✍评论⭐收藏
- ✨收录专栏:C语言每日一练
- ✨其他专栏:代码小游戏C语言初阶
- 🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,大家一起学习交流!🤗
【前言】
在大家学完初阶C语言后,有很多知识点是比较模糊的,我们应该多刷题,这样才能巩固我们所学知识。所以我开了一个新专栏C语言每日一刷,每一篇都包含5道选择题,2道编程题,每一道题后面都会有详细的解析。这个系列每日一更,大家来看看吧!
一、选择题
1、以下程序段的输出结果是( )
#include<stdio.h>
int main()
{char s[] = "\\123456\123456\t";printf("%d\n", strlen(s));return 0;
}A: 12 B: 13 C: 16 D: 以上都不对
【答案】A
【解析】
strlen() 函数用于获取字符串的长度(即字符中字符的个数,不包括\0)。\\、\123、\t是转义字符,所以长度是12。
\\表示单个字符
\123 表示八进制的ASCII码值为123对应的字符
It 表示制表符
很多小伙伴会忘记转义字符的具体内容,这里有常用转义字符。

2、若有以下程序,则运行后的输出结果是( )
#include<stdio.h>
#define N 2
#define M N + 1
#define NUM (M + 1) * M / 2
int main()
{printf("%d\n", NUM);return 0;
}A: 4 B: 8 C: 9 D: 6
【答案】B
【解析】
因为#define是宏定义,仅仅是直接替换,这里2替换N,N+1替换M,所以NUM为(N+1+1)*N+1/2=4*2+0=8,选B。
3、如下函数的 f(1) 的值为( )
int f(int n)
{static int i = 1;if(n >= 5)return n;n = n + i;i++;return f(n);
}A: 5 B: 6 C: 7 D: 8
【答案】C
【解析】
静态变量static只会被初始化一次,所以
第一次调用f(1):n=2;i=2;调用f(2)
第二次调用f(1):n=4;i=3;调用f(4)
第三次调用f(1):n=7;i=2;调用f(7)
第四次调用f(1):返回7
所以最终函数返回结果为7,选C。
4、下面3段程序代码的效果一样吗( )
int b;
(1)const int *a = &b;
(2)int const *a = &b;
(3)int *const a = &b;A: (2)=(3) B: (1)=(2) C: 都不一样 D: 都一样
【答案】B
【解析】
const修饰指针变量的效果,是根据const和*之间的相对位置来决定的 const放在*的左边意味着对应的指针不能被修改,放在*的右边意味着指针所指向的内容不能被修改。那么观察题目我们只需要找相对位置一样的即可,不难发现,(1)和(2)const和*的相对位置都是const在*的右边,故效果一样,而(3)的const放在*的右侧,效果不一样。故选B
5、对于下面的说法,正确的是( )
A.对于 struct X{short s;int i;char c;},sizeof(X)等于sizeof(s) + sizeof(i) + sizeof(c)
B.对于某个double变量 a,可以使用 a == 0.0 来判断其是否为零
C.初始化方式 char a[14] = "Hello, world!"; 和char a[14]; a = "Hello, world!";的效果相同
D.以上说法均不对
【答案】D
【解析】
A结构体要按高位对齐,int占四个字节,short占两个,char占一个字节,所以4+4+4=12;
B要判断一个双精度浮点数:if(abs(f) <= 1e-15)
C数组初始化两种方式:一种逐个赋值char a[14]={'H','e','I','I','o'};另一种char a[14]="Hello,world!"
所以选D。
二、编程题
1.OJ链接【牛客网题号: HJ76 尼科彻斯定理】【难度:简单】
验证尼科彻斯定理,即:任何一个整数 m 的立方都可以写成 m 个连续奇数之和。例如:
1^3=1
2^3=3+5
3^3=7+9+11
4^3=13+15+17+19输入一个正整数 m(m≤100) ,将 m 的立方写成 m 个连续奇数之和的形式输出。
注意:本题含有多组输入数据。
输入描述:输入一个int整数
输出描述:输出分解后的string
示例:
输入:6
输出:31+33+35+37+39+41
#include<stdio.h>
int main()
{int m = 0;while (scanf("%d", &m)){int i = 0;int ret = m * (m - 1) + 1;for (i = 1; i <= m; i++){printf("%d", ret);ret += 2;if (m != i)printf("+");}printf("\n");}return 0;
}2.OJ链接【牛客网题号: HJ100 等差数列】【难度:简单】
等差数列 2,5,8,11,14, ... 。(从 2 开始的 3 为公差的等差数列),求等差数列前 n 项和。
注意:本题有多组输入
输入描述:输入一个正整数 n 。
输出描述:输出一个相加后的整数。
示例:
输入:2 输入:275
输出:7 输出:113575
说明:2+5=7 说明:2+5+...+821+824=113575
#include<stdio.h>
int main()
{int n = 0;while (scanf("%d", &n)){printf("%d\n", (3 * n + 1) * n / 2);}return 0;
}好了,今天的每日一刷就到这里结束了,感谢大家的观看!

相关文章:

C语言暑假刷题冲刺篇——day2
目录 一、选择题 二、编程题 🎈个人主页:库库的里昂 🎐CSDN新晋作者 🎉欢迎 👍点赞✍评论⭐收藏✨收录专栏:C语言每日一练 ✨其他专栏:代码小游戏C语言初阶🤝希望作者的文章能对你…...

springcloud3 hystrix实现服务降级的案例配置2
一 服务降级的说明 1.1 服务降级说明 "服务器忙,请稍后在试"不让客户达等待,立即返回一个友好的提示。 1.2 服务降级的触发情况 1.程序运行异常; 2.超时; 3.服务熔断触发服务降级;4 .线程池/信号量打…...

第 3 章 稀疏数组和队列(1)
3.1 稀疏 sparsearray 数组 3.1.1先看一个实际的需求 编写的五子棋程序中,有存盘退出和续上盘的功能。 分析问题: 因为该二维数组的很多值是默认值 0.因此记录了很多没有意义的数据.->稀疏数组 3.1.2基本介绍 当一个数组中大部分元素为 0,或者为同…...

7-10 奇偶分家
分数 10 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 给定N个正整数,请统计奇数和偶数各有多少个? 输入格式: 输入第一行给出一个正整N(≤1000);第2行给出N个非负整数,以空格分隔。 输…...

使用词向量以数学方式查找具有相似含义的单词
摄影:Nika Charakova 一、说明 简而言之,词向量只不过是表示自然语言词含义的一系列实数。这项技术是有用的NLP功能的重要推动力,使机器能够“理解”人类语言。本文讨论如何使用词向量以编程方式计算文本的语义相似性,例如&#x…...

opencv实现以图搜图
这里写目录标题 1. 步骤1.1 导入OpenCV库:1.2 加载图像1.3 提取特征1.4 匹配特征1.5 显示结果 2. 完整代码3. 测试图片及效果 1. 步骤 1.1 导入OpenCV库: 在您的C代码中,首先需要导入OpenCV库。您可以使用以下语句导入核心模块:…...

爬虫工作中代理失效了怎么处理?
Hey!亲爱的爬虫小伙伴们,是不是经常在爬虫的工作中遇到代理IP失效的问题?别着急,今天我来分享一些应对代理失效的妙招!这些方法简单易行,让你爬虫顺利进行. 一、为什么代理会失效? 在爬虫过程…...
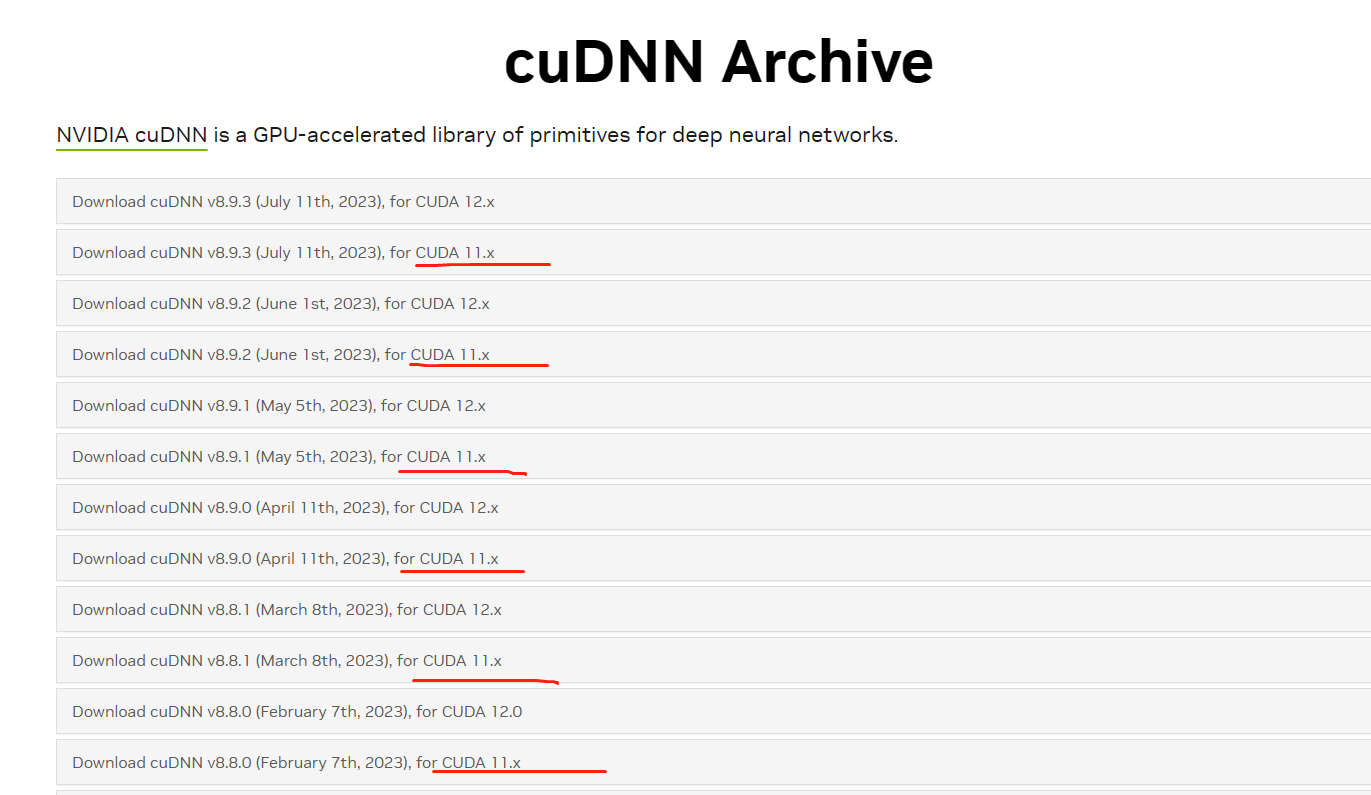
使用虚拟环境conda安装不同版本的cuda,cudnn,pytorch
背景:在学习深度学习时,我们不可避免的需要跑多个神经网络,而不同的神经网络环境都不一样,所以必须要使用到虚拟环境(如conda)去做环境隔离,安装属于自己的环境。在这环境中,大多神经网络都必须要用到cuda&…...
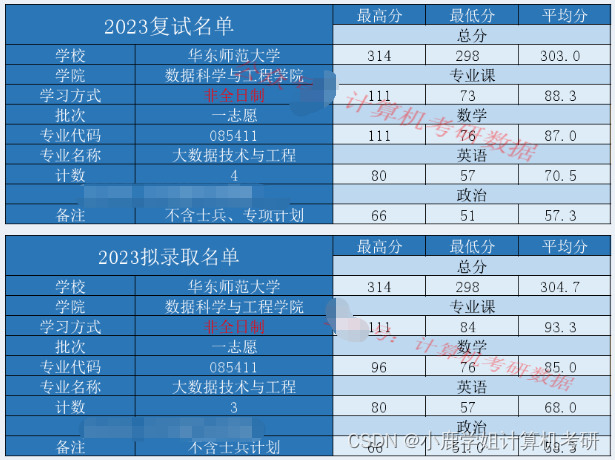
【24择校指南】华东师范大学计算机考研考情分析
华东师范大学(B) 考研难度(☆☆☆☆) 内容:23考情概况(拟录取和复试分数人数统计)、院校概况、23考试科目、23复试详情、各科目及专业考情分析。 正文2563字,预计阅读:3分钟。 2023考情概况…...
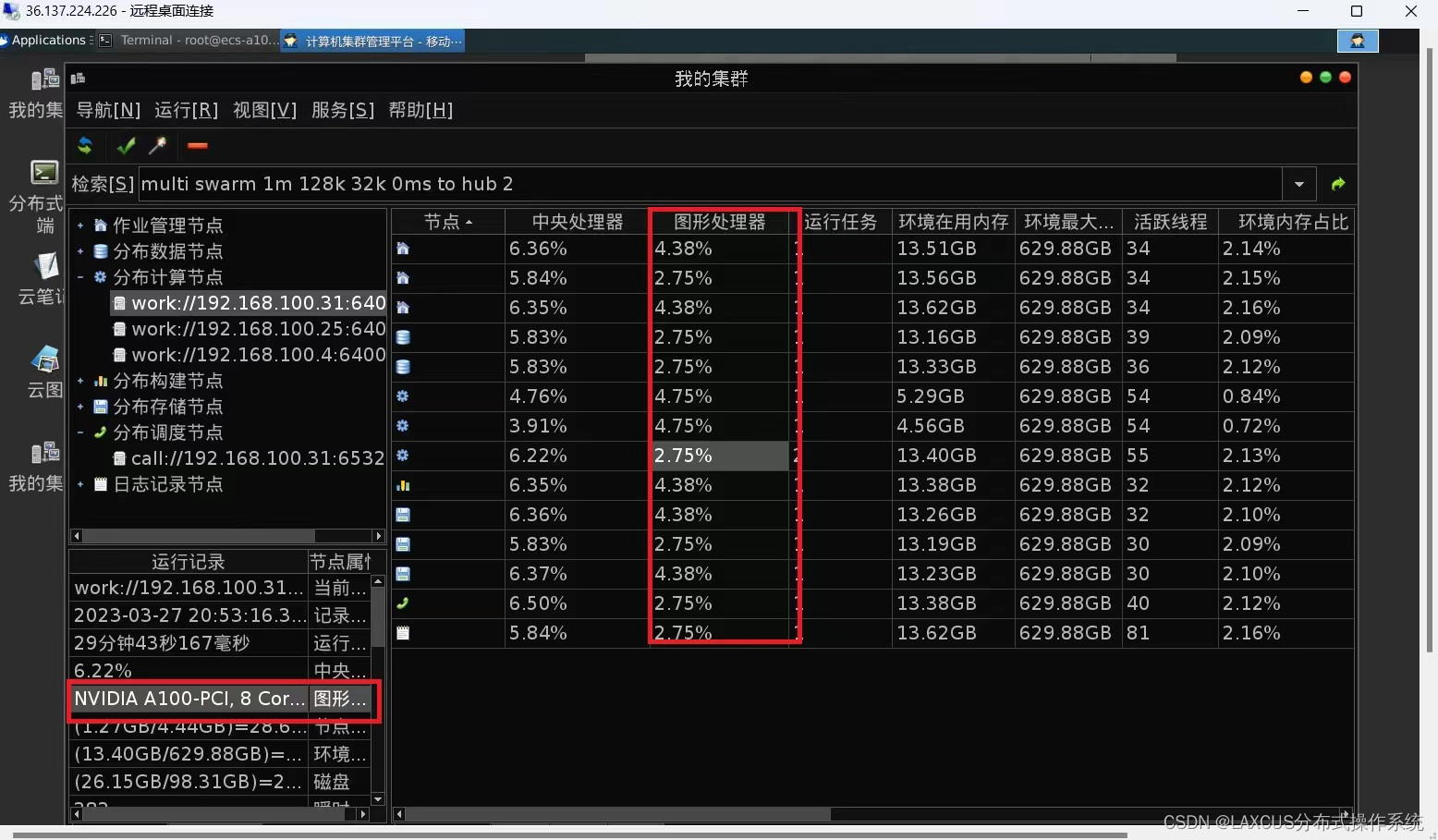
什么是LAXCUS分布式操作系统?
相较Linux、Windows,Laxcus是同时在多台计算机上运行的操作系统,处理大规模、高并发、高性能业务,其特点是资源共享和任务并行,并实现【数存算管】超融合一体化。环境中的资源:CPU、GPU、内存、硬盘、网络,…...

Redis数据结构——链表list
链表是一种常用的数据结构,提供了顺序访问的方式,而且高效地增删操作。 Redis中广泛使用了链表,例如:列表的底层实现之一就是链表。 在Redis中,链表分为两部分:链表信息 链表节点。 链表节点用来表示链表…...

[自学记录06|*百人计划]Gamma矫正与线性工作流
一、前言 Gamma矫正其实也属于我前面落下的一块内容,打算把它补上,其它的没补是因为我之前写的GAMES101笔记里已经涵盖了,而Gamma矫正在101里面确实没提到,于是打算把它补上,这块内容并不难,但是想通透的理…...

【数据结构】二叉树链式结构的实现及其常见操作
目录 1.手搓二叉树 2.二叉树的遍历 2.1前序、中序以及后序遍历 2.2二叉树的层序遍历 3.二叉树的常见操作 3.1求二叉树节点数量 3.2求二叉树叶子节点数量 3.3求二叉树第k层节点个数 3.3求二叉树的深度 3.4二叉树查找值为x的节点 4.二叉树的销毁 1.手搓二叉树 在学习…...
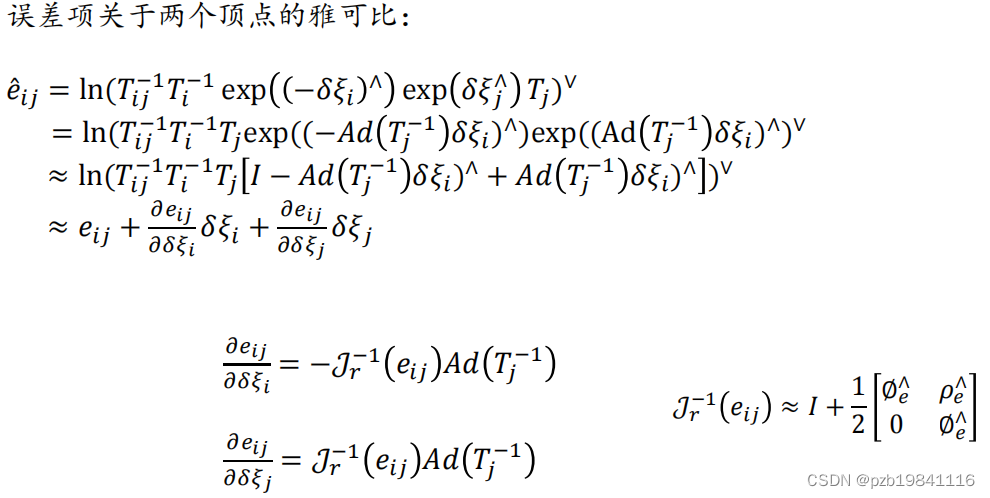
从零实战SLAM-第九课(后端优化)
在七月算法报的班,老师讲的蛮好。好记性不如烂笔头,关键内容还是记录一下吧,课程入口,感兴趣的同学可以学习一下。 --------------------------------------------------------------------------------------------------------…...

Python Opencv实践 - 图像金字塔
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_COLOR) print(img.shape)#图像上采样 #cv.pyrUp(src, dstNone, dstsizeNone, borderTypeNone) #参考资料:https://blo…...
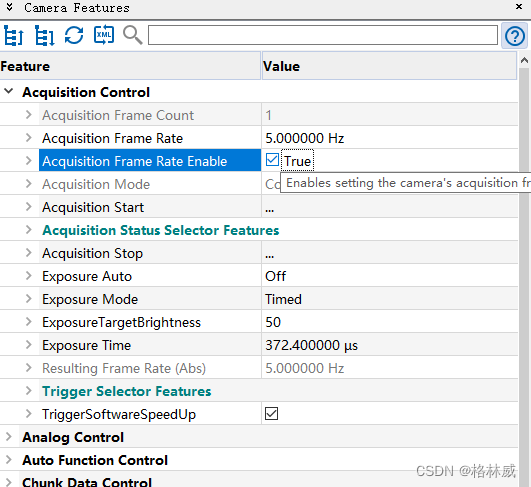
Baumer工业相机堡盟工业相机如何通过BGAPI SDK设置相机的固定帧率(C++)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK设置相机的固定帧率(C) Baumer工业相机Baumer工业相机的固定帧率功能的技术背景CameraExplorer如何查看相机固定帧率功能在BGAPI SDK里通过函数设置相机固定帧率 Baumer工业相机通过BGAPI SDK设置相机固定帧…...
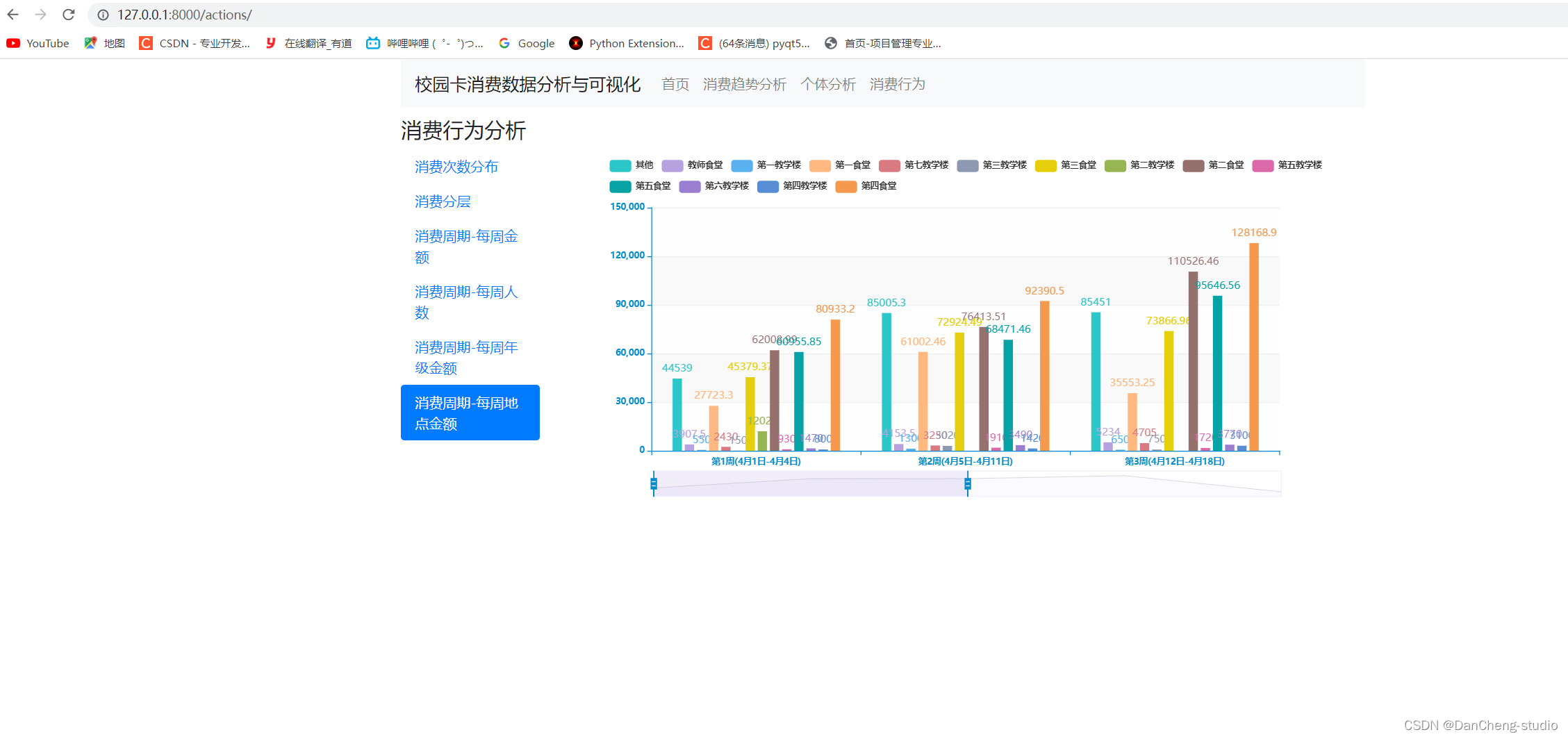
计算机竞赛 python+大数据校园卡数据分析
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于yolov5的深度学习车牌识别系统实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:4分工作量:4分创新点:3分 该项目较为新颖&am…...

DNNGP模型解读-early stopping 和 batch normalization的使用
一、考虑的因素(仅代表个人观点) 1.首先我们看到他的这篇文章所考虑的不同方面从而做出的不同改进,首先考虑到了对于基因组预测的深度学习方法的设计 ,我们设计出来这个方法就是为了基因组预测而使用,这也是主要目的&…...
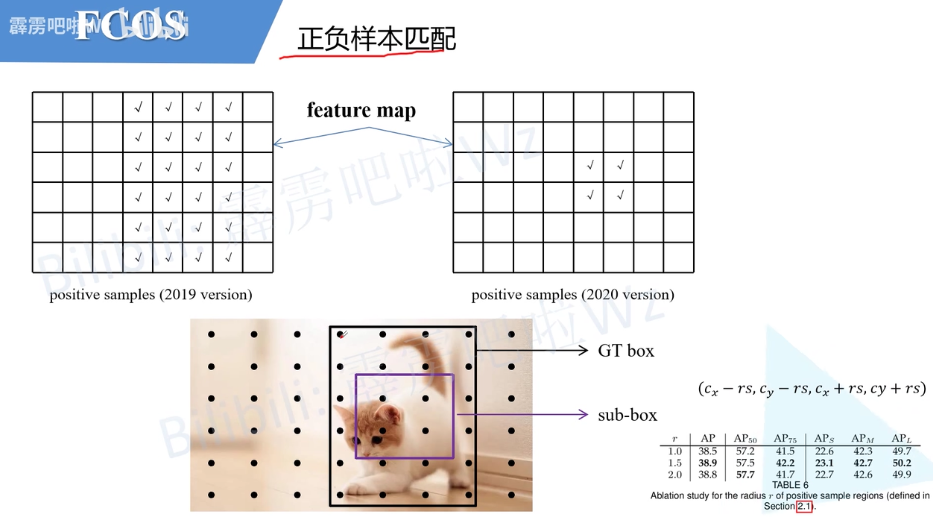
【目标检测】目标检测 相关学习笔记
目标检测算法 PASCALVOC2012数据集 挑战赛主要分为 图像分类 目标检测 目标分割 动作识别 数据集分为四个大类 交通(飞机 船 公交车 摩托车) 住房(杯子 椅子 餐桌 沙发) 动物(鸟 猫 奶牛 狗 马 羊) 其他&a…...
)
面试攻略,Java 基础面试 100 问(十六)
反射使用步骤(获取Class对象、调用对象方法) 获取想要操作的类的Class对象,他是反射的核心,通过Class对象我们可以任意调用类的方法。 调用 Class 类中的方法,既就是反射的使用阶段。 使用反射 API 来操作这些信息。 什么是 java 序列化&…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
