Leetcode Top 100 Liked Questions(序号53~74)
53. Maximum Subarray
题意:一个数组,找到和最大的子串
我的思路
我记得好像On的动态规划来做的?但是想不起来了,先死做,用的前缀和——TLE超时
那就只能想想dp怎么做了
假设dp[i]表示的是以 i 为右端点的最大的子串,dp[0]是自己;
i=1时,如果dp[0]小于0,dp[1]=nums[1],否则dp[1]=dp[0]+nums[1]
i=2时,如果dp[1]小于0,dp[2]=nums[2],否则dp[2]=dp[2-1]+nums[2]
所以状态转移方程为:如果dp[i - 1]小于0,dp[ i ]=nums[ i ],否则dp[ i ]=dp[i -1]+nums[ i ]
On解决,同时dp换成nums还能更省空间
代码 Runtime 87 ms Beats 78.76% Memory67.9 MB Beats 8.86%
class Solution {
public:int maxSubArray(vector<int>& nums) {int n=nums.size();int maxx=nums[0];for(int i=1;i<n;i++){if(nums[i-1]>0) nums[i]=nums[i]+nums[i-1];maxx=max(maxx,nums[i]);}return maxx;}
};如果想跟快的话,取消同步 Runtime 50 ms Beats 99.91% Memory 67.7 MB Beats 81.53%
class Solution {
public:int maxSubArray(vector<int>& nums) {ios_base::sync_with_stdio(false);cin.tie(NULL); cout.tie(NULL);int n=nums.size();int maxx=nums[0];for(int i=1;i<n;i++){if(nums[i-1]>0) nums[i]=nums[i]+nums[i-1];maxx=max(maxx,nums[i]);}return maxx;}
};标答补充 分治
看看分治的代码
分成左右中三个部分,左边部分是左边最大的子串和,右边部分得到右边最大字串和;
左边部分是所有包含了m-1位置的字符串的最大子串和 lmax,右边部分是包含了m+1位置的字符串的最大字串和 rmax,返回max(lmax. rmax ),ml+mr+nums[m]两者之中大的那一个
代码 Runtime110 ms Beats 65.10% Memory 67.9 MB Beats 8.86%
class Solution {
public:int maxSubArray(vector<int>& nums) {return maxSubArray(nums, 0, nums.size() - 1);}
private:int maxSubArray(vector<int>& nums, int l, int r) {if (l > r) return INT_MIN;int m = l + (r - l) / 2, ml = 0, mr = 0;int lmax = maxSubArray(nums, l, m - 1);int rmax = maxSubArray(nums, m + 1, r);for (int i = m - 1, sum = 0; i >= l; i--) {sum += nums[i];ml = max(sum, ml);}for (int i = m + 1, sum = 0; i <= r; i++) {sum += nums[i];mr = max(sum, mr);}return max(max(lmax, rmax), ml + mr + nums[m]);}
};54. Spiral Matrix
题意: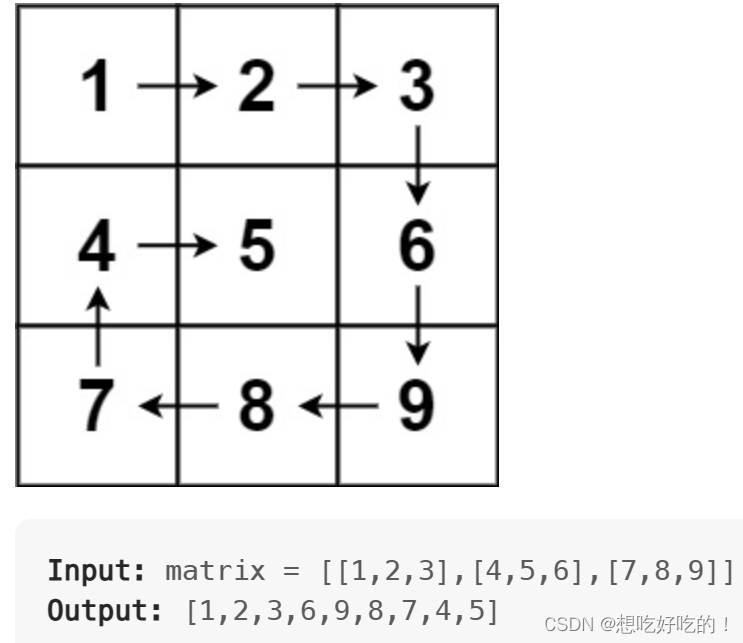
我的思路
死做
代码 Runtime 0 ms Beats 100% Memory6.9 MB Beats 61.55%
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int dy[]={1, 0,-1,0};int dx[]={0, 1, 0,-1};bool vis[19][19]={0};int m=matrix.size(),n=matrix[0].size();int nowx=0,nowy=0,mod=0;int nx=0,ny=0;vector<int> ans;for(int i=0;i<m*n;i++){//首先循环一开始的新来的一定是可以的nowx=nx,nowy=ny;vis[nowx][nowy]=1;ans.push_back(matrix[nowx][nowy]);if(i+1==m*n)break;nx=nowx+dx[mod];ny=nowy+dy[mod];while(nx<0||nx>=m||ny<0||ny>=n||vis[nx][ny]==1){mod=(mod+1)%4;nx=nowx+dx[mod];ny=nowy+dy[mod];}}return ans;}
};55. Jump Game
题意:问能不能从索引0到索引n-1
我的思路
既然是问能不能到到终点,用贪心或者动态规划都可以,上次用了动态规划,这次就贪心吧
注意:记得 if(nums[0]==0&&n!=1)return 0;要特判
代码 Runtime 43 ms Beats 93.40% Memory48.3 MB Beats 74.51%
class Solution {
public:bool canJump(vector<int>& nums) {int n=nums.size();if(nums[0]==0&&n!=1)return 0;for(int i=1;i<n-1;i++){nums[i]=max(nums[i]+i,nums[i-1]);if(nums[i]==i)return 0;}return 1;}
};56. Merge Intervals
题意:返回重叠部分

我的思路
应该是要维护两端端点的,好像是-1 +1什么的?
做着做着发现这个interval还有start==end,这个-1和+1怎么做??
点的话就找一个bool数组特判吧
代码 Runtime19 ms Beats 99.65% Memory19.2 MB Beats 31.70%
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& in) {int vis[10004]={0};int n=in.size();int maxx=0;bool fl[10004]={0};//判点vector<vector<int>> ans;for(int i=0;i<n;i++){int st=in[i][0],en=in[i][1];maxx=max(maxx,en);if(st==en)fl[st]=1;else vis[st]++,vis[en]--;}int st=0,en=0,sum=0;int mod=1;//mod1是找正数,找到正数了切换mod-1找负数for(int i=0;i<=maxx;i++){sum=sum+vis[i];if(mod==1&&sum>0){st=i;mod=-mod;}else if(mod==-1&&sum==0){en=i;mod=-mod;ans.push_back({st,en});}else if(fl[i]&&mod==1){ans.push_back({i,i});}}return ans;}
};标答 排序
标答的时间复杂度为O(n+logn)
首先将interval排序,应该是按照覆盖的起点排序,起点从小到大排序;
遍历每个覆盖域,首先是第一个覆盖区域,初始化start和end;之后不断地找大的end,直到目前最大的end小于新来的start,这时把起点和重点放到答案列表中,更新起点和终点
代码 Runtime 23 ms Beats 98.10% Memory19 MB Beats 71.5%
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> ans;int n=intervals.size();sort(intervals.begin(),intervals.end());int start=intervals[0][0];int end=intervals[0][1];for(int i=1;i<n;i++){if(end<intervals[i][0]){ans.push_back({start,end});start=intervals[i][0];end=intervals[i][1];}else{end=max(intervals[i][1],end);}}ans.push_back({start,end});return ans;}
};62. Unique Paths
题意:机器人只能向下或者向右走,要从grid[0][0]走到grid[m-1][n-1]
我的思路
好像是组合数?按按计算器看看能不能推出来,没推出来
好像递归也是能够做出来的?不过走楼梯是一维的c[i+1]+c[i+2]得到的?
那么假设c是方案数,就先按照下面这个图建立一个二维数组做?
【看标答,这种方法居然是dp】
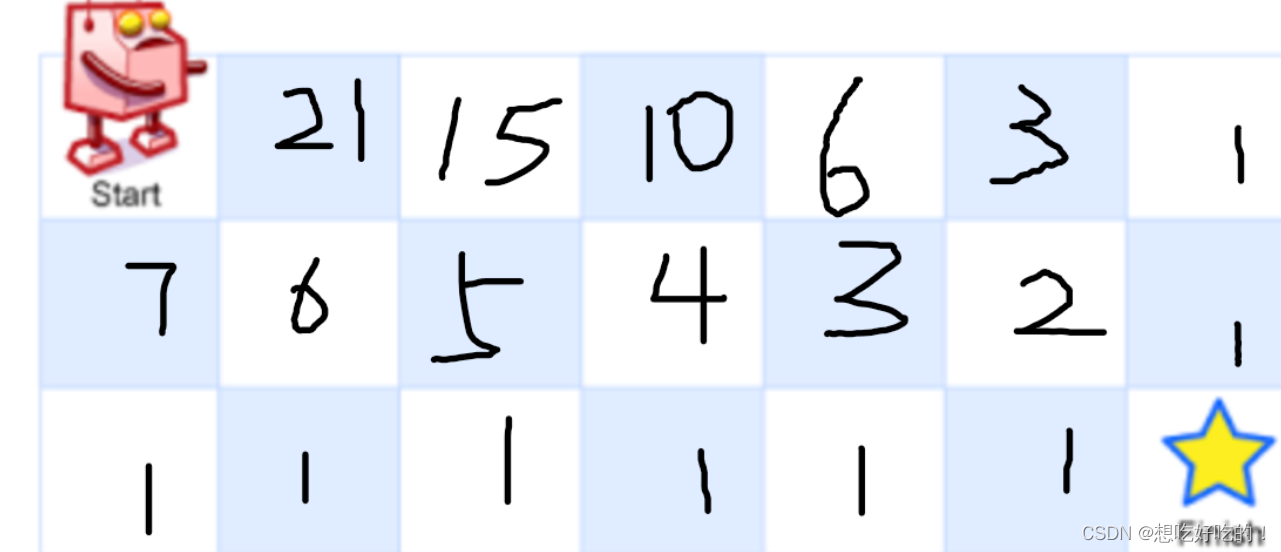
代码 Runtime 0 ms Beats 100% Memory6 MB Beats 87.9%
class Solution {
public:int uniquePaths(int m, int n) {int st[104][104]={0};st[m-1][n-1]=1;for(int i=m-1;i>=0;i--)for(int j=n-1;j>=0;j--)st[i][j]+=(st[i+1][j]+st[i][j+1]);return st[0][0];}
};标答 组合数
在这个图上,一共要走m+n-2步,其中有m-1步是向下的,n-1步是向右的,这可以转换成m-1个向下和n-1个向右的排序(图源知乎)

代码 Runtime 0 ms Beats 100.00% Memory 6 MB Beats 87.9%
class Solution {
public:int uniquePaths(int m, int n) {int N = n+m-2; // total steps = n-1 + m-1int r = min(n,m)-1;
// will iterate on the minimum for efficiency = (total) C (min(right, down)double res = 1;// compute nCrfor(int i=1; i<=r; ++i, N--)res = res*(N)/i;return (int)res;}
};64. Minimum Path Sum
题意:二维地图,只能向下或者向右走,找到所有路径上的最小的值。
我的思路
这个肯定是dp吧;还是相同的道理,但是要注意边缘处理
dp[i][j]=num[i][j]+min(dp[i+1][j],dp[i][j+1])
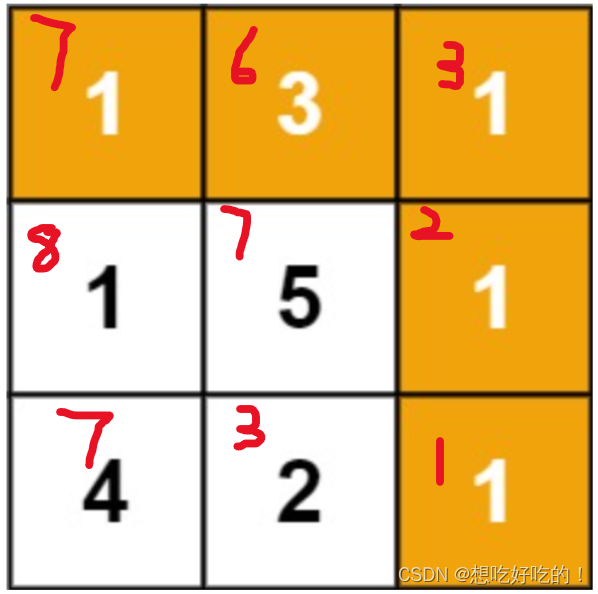
代码 Runtime 6 ms Beats 88.72% Memory 9.7 MB Beats 89.19%
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m=grid.size(),n=grid[0].size();for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){if(i==m-1 && j==n-1)continue;if(i==m-1)grid[i][j]+=grid[i][j+1];else if(j==n-1)grid[i][j]+=grid[i+1][j];else grid[i][j]+=min(grid[i+1][j],grid[i][j+1]);}}return grid[0][0];}
};70. Climbing Stairs
题意:爬楼梯,只能走1或2步,问到终点要走多少步
我的思路
n=1,c=1;n=2,c=2;n=3,c=3;c[i]=c[i-1]+c[i-2]
代码 Runtime 0 ms Beats 100% Memory 5.9 MB Beats 94.85%
class Solution {
public:int climbStairs(int n) {if(n<3) return n;int a=1,b=2,c=0;for(int i=3;i<=n;i++){c=a+b;a=b;b=c;}return c;}
};72. Edit Distance
题意:三个操作:插入一个字母,删除一个字母,替换一个字母;问从字符串1变成字符串2最少需要多少步?
我的思路
应该是用动态规划
假设
相关文章:

Leetcode Top 100 Liked Questions(序号53~74)
53. Maximum Subarray 题意:一个数组,找到和最大的子串 我的思路 我记得好像On的动态规划来做的?但是想不起来了,先死做,用的前缀和——TLE超时 那就只能想想dp怎么做了 假设dp[i]表示的是以 i 为右端点的最大的…...
Rabbitmq消息不丢失
目录 一、消息不丢失1.消息确认2.消息确认业务封装2.1 发送确认消息测试2.2 消息发送失败,设置重发机制 一、消息不丢失 消息的不丢失,在MQ角度考虑,一般有三种途径: 1,生产者不丢数据 2,MQ服务器不丢数据…...
Kotlin runBlocking launch多个协程读写mutableListOf时序
Kotlin runBlocking launch多个协程读写mutableListOf时序 import kotlinx.coroutines.delay import kotlinx.coroutines.launch import kotlinx.coroutines.runBlockingfun main(args: Array<String>) {var lists mutableListOf<String>()runBlocking {launch {r…...

Spring Cloud微服务治理框架深度解析
在学习一个技术之前,首先我们要了解它是做什么的,我们为什么要用它。不然看再多资料都理解不了,因此我们先来讲解下Spring Cloud Spring Cloud是一套微服务治理框架,几乎考虑到了微服务治理的方方面面。那么接下来具体说下 Spring…...

设计模式之原型模式Prototype的C++实现
1、原型模式提出 在软件功能设计中,经常面临着“某些结构复杂的对象”的创建工作,且创建的对象想拥有其他对象在某一刻的状态,则可以使用原型模型。原型模型是通过拷贝构造函数来创建对象,并且该对象拥有其他对象在某一刻的状态。…...
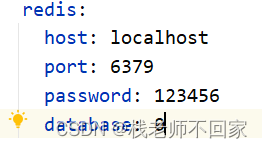
Java 中操作 Redis
文章目录 一、Redis 常用数据类型二、Redis 常用操作命令1. 字符串命令2. 哈希命令3. 列表命令4. 集合命令5. 有序集合命令6. 通用命令 三、在 Java 中操作 Redis1. 导入 maven 坐标2. 配置 Redis 数据源3. 编写配置类 四、在代码中的具体使用 一、Redis 常用数据类型 Redis 存…...
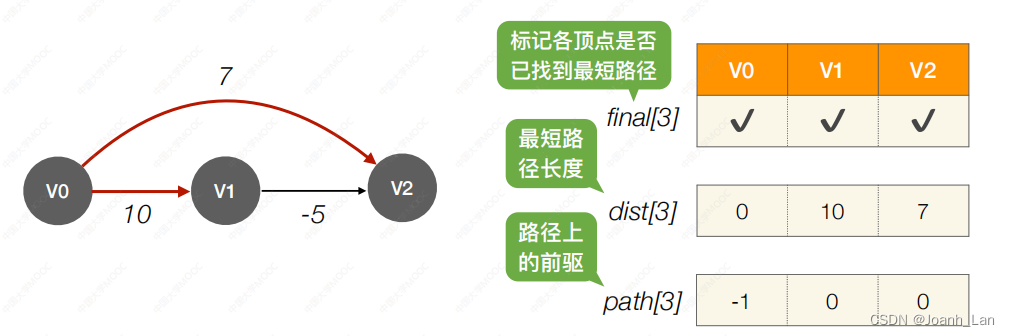
数据结构--最短路径 Dijkstra算法
数据结构–最短路径 Dijkstra算法 Dijkstra算法 计算 b e g i n 点到各个点的最短路 \color{red}计算\ begin\ 点到各个点的最短路 计算 begin 点到各个点的最短路 如果是无向图,可以先把无向图转化成有向图 我们需要2个数组 final[] (标记各顶点是否已…...
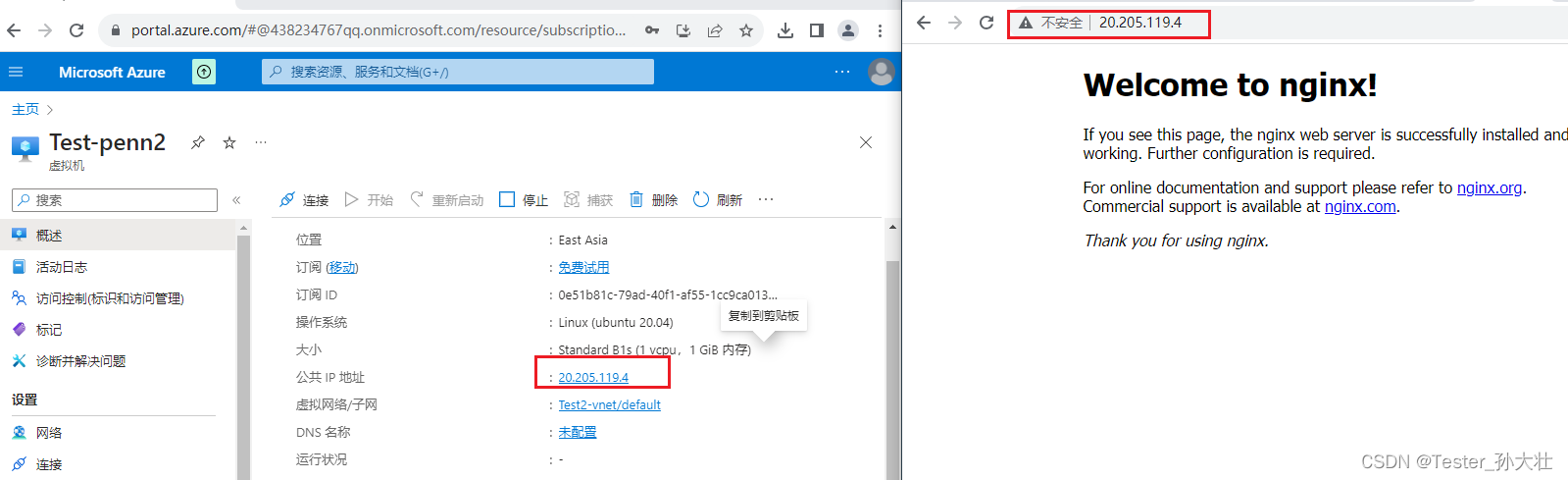
在 Linux 虚拟机上使用 Azure 自定义脚本扩展版本
参考 azure创建虚拟机,创建虚拟机注意入站端口规则开放80端口、 2.转到资源,点击扩展应用程序,创建存储账户,创建容器,上传文件,选择文件,会自动执行部署。 apt-get update -y && apt-get insta…...
W5500-EVB-PICO 做UDP Server进行数据回环测试(七)
前言 前面我们用W5500-EVB-PICO 开发板在TCP Client和TCP Server模式下,分别进行数据回环测试,本章我们将用开发板在UDP Server模式下进行数据回环测试。 UDP是什么?什么是UDP Server?能干什么? UDP (User Dataqram P…...
:项目实战(二)--elasticsearch java api 进行数据增删改查)
ES搜索引擎入门+最佳实践(九):项目实战(二)--elasticsearch java api 进行数据增删改查
本篇是这个系列的最后一篇了,在这之前可以先看看前面的内容: ES搜索引擎入门最佳实践(一)_flame.liu的博客-CSDN博客 ES搜索引擎入门最佳实践(二)_flame.liu的博客-CSDN博客 ES搜索引擎入门最佳实践(三)_flame.liu的博客-CSDN博客 ES搜索引擎入门最佳实践(四)_flame.liu的博…...
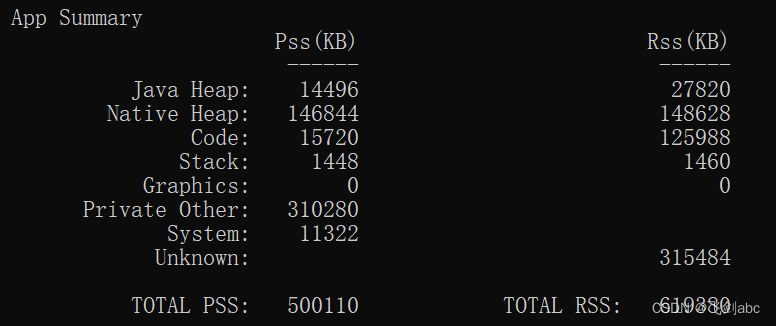
android内存分析工具记录,请利用好最后2个神器
相机见证了java内存暴增和native持续增长的问题,因此这里记录一下使用的工具情况,方便后续继续使用 一、java 内存 如果是java层的内存可以直接借助leakCanary工具,配置也很简单,直接在build.gradle中添加依赖即可: …...

安科瑞变电所运维平台在电力系统中应用分析
摘要:现代居民生活、工作对电力资源的需求量相对较多,给我国的电力产业带来了良好的发展机遇与挑战。探索电力系统基本构成, 将变电运维安全管理以及相应的设备维护工作系统性开展,能够根据项目实践工作要求,将满足要求…...
uniapp开发微信小程序使用painter将页面转换为图片并保存到本地相册
引言 我使用到painter的原因是,在uniapp开发微信小程序时,需要将一个页面的内容转换成图片保存到本地相册。 起初在网上找到很多都是在uniapp中使用 html2canvas 将网页转换成图片再jspdf将图片转换为pdf,但是这种方式在小程序环境不支持&am…...

790. 数的三次方根
文章目录 QuestionIdeasCode Question 给定一个浮点数 n ,求它的三次方根。 输入格式 共一行,包含一个浮点数 n 。 输出格式 共一行,包含一个浮点数,表示问题的解。 注意,结果保留 6 位小数。 数据范围 −10000≤…...

POSTGRESQL 关于2023-08-14 数据库自动启动文章中使用KILL 来进行配置RELOAD的问题解释...
开头还是介绍一下群,如果感兴趣Polardb ,mongodb ,MySQL ,Postgresql ,redis ,SQL SERVER ,ORACLE,Oceanbase 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请加 liuaustin3微信号 &…...

vue 使用插件高德地图--vue-amap
第一步:安装 vue-amap npm install vue-amap第二步:在你的 Vue 项目中注册 vue-amap: // main.js import Vue from vue; import VueAMap from vue-amap;Vue.use(VueAMap);VueAMap.initAMapApiLoader({// 高德开发者平台申请key值key: cc9c098…...

减速比如何计算
减速比是用来衡量机械系统中输入轴和输出轴转速之间的比例关系,通常用来描述传动装置(如齿轮传动、皮带传动等)的效果。计算减速比的公式取决于传动装置的类型。以下是一些常见传动装置的减速比计算方法: 齿轮传动: 对…...
)
HarmonyOS/OpenHarmony应用开发-ArkTSAPI组件总体分类与说明(下)
六、文本与输入 Text 显示一段文本的组件。 Span 作为Text组件的子组件,用于显示行内文本片段的组件。 Search 搜索框组件,适用于浏览器的搜索内容输入框等应用场景。 TextArea 多行文本输入框组件,当输入的文本内容超过组件宽度时会自动换行…...

势函数和鞅的停时定理
前置芝士 鞅: 鞅是一类特殊的随机过程,假设我们从一开始就在观察一场赌博游戏,现在已经得到了前t秒的观测值,那么当第t1 秒观测值的期望等于第t秒的观测值时,我们称这是一个公平赌博游戏。 具体来说,对于…...

途乐证券-炒股开户流程是怎样的?
炒股是一种危险较大但收益也相对较高的出资方法,而开户则是出资炒股的前提。跟着科技的开展,炒股开户已经能够在线完结,但流程相对来说仍是比较繁琐的。那么,炒股开户流程是怎样的呢?下面从多个视点剖析。 一、炒股开户…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

智能体革命:企业如何构建自主决策的AI代理?
OpenAI智能代理构建实用指南详解 随着大型语言模型(LLM)在推理、多模态理解和工具调用能力上的进步,智能代理(Agents)成为自动化领域的新突破。与传统软件仅帮助用户自动化流程不同,智能代理能够自主执行工…...

Linux【5】-----编译和烧写Linux系统镜像(RK3568)
参考:讯为 1、文件系统 不同的文件系统组成了:debian、ubuntu、buildroot、qt等系统 每个文件系统的uboot和kernel是一样的 2、源码目录介绍 目录 3、正式编译 编译脚本build.sh 帮助内容如下: Available options: uboot …...

WEB3全栈开发——面试专业技能点P8DevOps / 区块链部署
一、Hardhat / Foundry 进行合约部署 概念介绍 Hardhat 和 Foundry 都是以太坊智能合约开发的工具套件,支持合约的编译、测试和部署。 它们允许开发者在本地或测试网络快速开发智能合约,并部署到链上(测试网或主网)。 部署过程…...
