数据结构--拓扑排序
数据结构–拓扑排序
AOV⽹
A O V ⽹ \color{red}AOV⽹ AOV⽹(Activity On Vertex NetWork,⽤顶点表示活动的⽹):
⽤ D A G 图 \color{red}DAG图 DAG图(有向⽆环图)表示⼀个⼯程。顶点表示活动,有向边 < V i , V j > <V_i, V_j> <Vi,Vj>表示活动Vi必须先于活动 V j V_j Vj进⾏
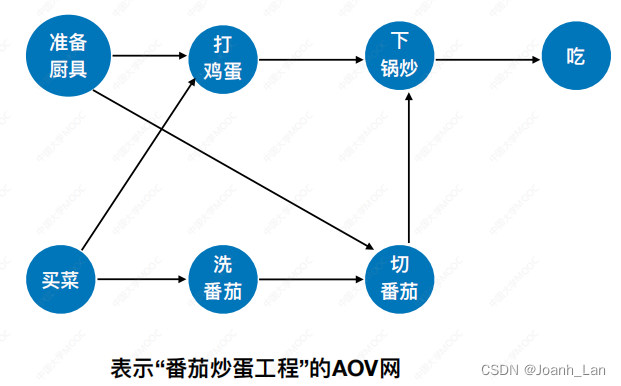
注:如果图中存在环路就不是 A O V 网 \color{red}注:如果图中存在环路就不是AOV网 注:如果图中存在环路就不是AOV网
DAG图是指有向无环图(Directed Acyclic Graph),是一种有向图的特殊形式。它由一些有向边连接的节点组成,并且不存在任何形式的环。换句话说,从任何一个节点出发,沿着有向边的方向无法经过一系列的节点再回到原始节点。DAG图常用于表示一些具有依赖关系的任务或事件,其中每个节点表示一个任务或事件,有向边表示任务或事件之间的依赖关系。DAG图在计算机科学和工程中有广泛的应用,例如任务调度、编译器优化、数据流分析等领域。
拓扑排序
拓扑排序 \color{red}拓扑排序 拓扑排序:在图论中,由⼀个 有向⽆环图 \color{red}有向⽆环图 有向⽆环图的顶点组成的序列,当且仅当满⾜下列条件时,称为该图的⼀个拓扑排序:
① 每个顶点出现且只出现⼀次。
② 若顶点A在序列中排在顶点B的前⾯,则在图中不存在从顶点B到顶点A的路径。或定义为:拓扑排序是对有向⽆环图的顶点的⼀种排序,它使得若存在⼀条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后⾯。每个AOV⽹都有⼀个或多个拓扑排序序列。
上图其中一个拓扑排序:

拓扑排序的实现:
① 从AOV⽹中选择⼀个没有前驱的顶点并输出。
② 从⽹中删除该顶点和所有以它为起点的有向边。
③ 重复①和②直到当前的AOV⽹为空或当前⽹中不存在⽆前驱的顶点为⽌。
注:拓扑排序序列可能有多个 \color{red}注:拓扑排序序列可能有多个 注:拓扑排序序列可能有多个
拓扑排序代码实现
王道书上代码



个人code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
bool topsort()
{int tt = -1, hh = 0;for(int i = 1; i <= n; i++)if(!d[i])q[++tt] = i;while(hh <= tt){int t = q[hh++];for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];d[j]--;if(!d[j]) q[++tt] = j;}}return tt == n - 1;
}
int main()
{cin >> n >> m;memset(h, -1, sizeof(h));for(int i = 0; i < n; i++){int a, b;cin >> a >> b;add(a, b);d[b]++;}if(topsort()){for(int i = 0; i < n; i++)cout << q[i] << ' ';cout << endl;}else cout << "-1" << endl;return 0;
}
判断是否存在拓扑序
时间复杂度 O(n + m), n 表示点数,m表示边数
bool topsort()
{int hh = 0, tt = -1;// d[i] 存储点i的⼊度for (int i = 1; i <= n; i ++ )if (!d[i])q[ ++ tt] = i;while (hh <= tt){int t = q[hh ++ ];for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (-- d[j] == 0)q[ ++ tt] = j;}}// 如果所有点都⼊队了,说明存在拓扑序列;否则不存在拓扑序列。return tt == n - 1;
}
逆拓扑排序

对⼀个AOV⽹,如果采⽤下列步骤进⾏排序,则称之为 逆拓扑排序 \color{red}逆拓扑排序 逆拓扑排序:
① 从AOV⽹中选择⼀个没有后继( 出度为 0 \color{red}出度为0 出度为0)的顶点并输出。
② 从⽹中删除该顶点和所有以它为终点的有向边。
③ 重复①和②直到当前的AOV⽹为空。
其中一个逆拓扑排序

逆拓扑排序代码实现

逆拓扑排序的实现(DFS算法)

DFS判断是否有环:
int vis[N], cnt; // timestamp
int per[N];
bool cyc[N];// 标记
void dfs(int u) //找环 & 标记环
{vis[u] = ++cnt;for (auto v : g[u]){if (per[u] == v)continue;if (!vis[v]){per[v] = u;dfs(v);}else if (vis[u] > vis[v]){for (int i = u; i != v; i = per[i])cyc[i] = true;cyc[v] = true;}}
}
如果单纯判断是否有环,只需要引进父结点(fa)
dfs(u,fa)
如果 u == fa 则存在环
知识点回顾与重要考点
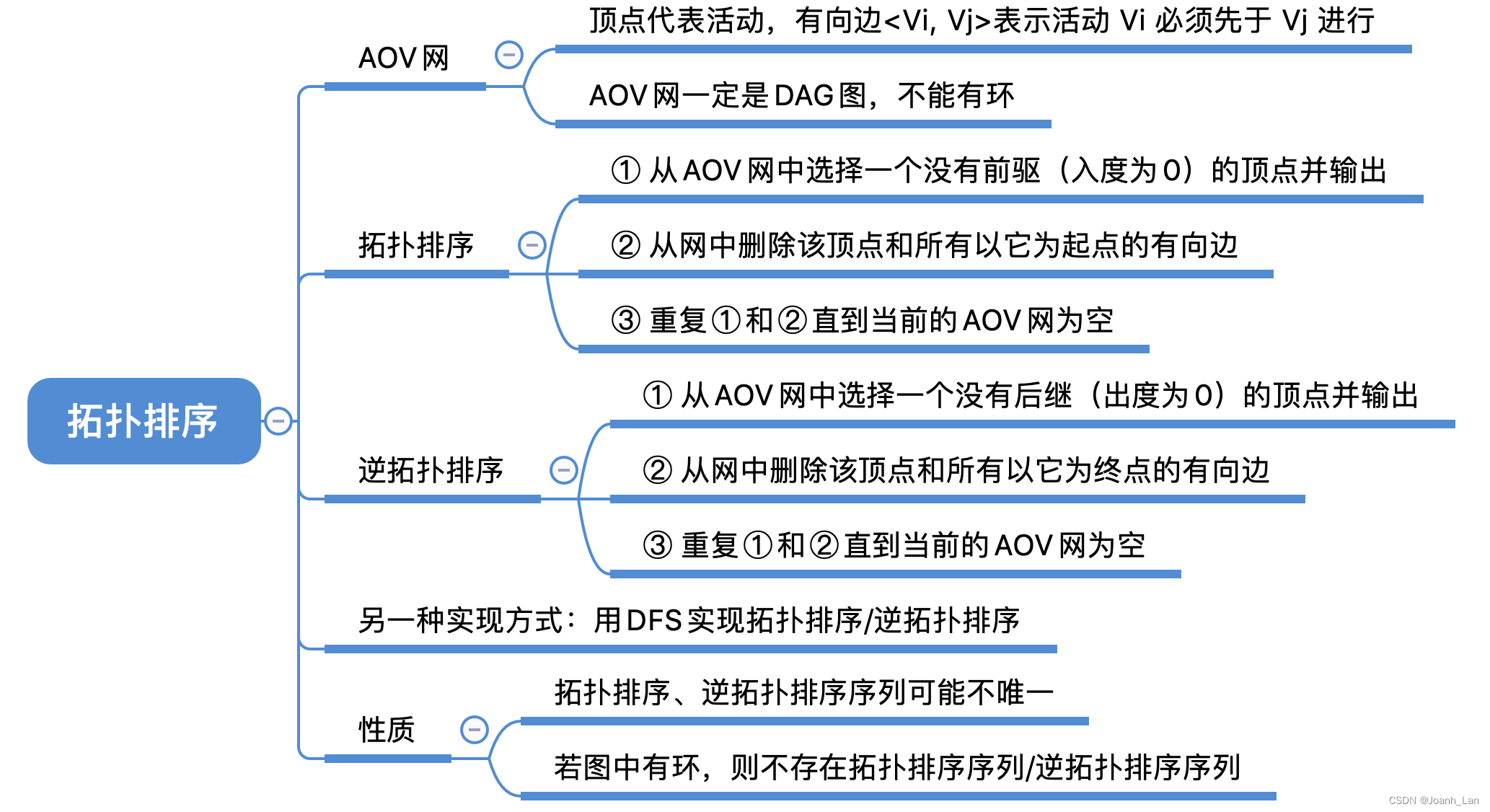
相关文章:

数据结构--拓扑排序
数据结构–拓扑排序 AOV⽹ A O V ⽹ \color{red}AOV⽹ AOV⽹(Activity On Vertex NetWork,⽤顶点表示活动的⽹): ⽤ D A G 图 \color{red}DAG图 DAG图(有向⽆环图)表示⼀个⼯程。顶点表示活动,有向边 < V i , V j …...

算法竞赛备赛之搜索与图论训练提升,暑期集训营培训
目录 1.DFS和BFS 1.1.DFS深度优先搜索 1.2.BFS广度优先搜索 2.树与图的遍历:拓扑排序 3.最短路 3.1.迪杰斯特拉算法 3.2.贝尔曼算法 3.3.SPFA算法 3.4.多源汇最短路Floy算法 4.最小生成树 4.1.普利姆算法 4.2.克鲁斯卡尔算法 5.二分图:染色法…...
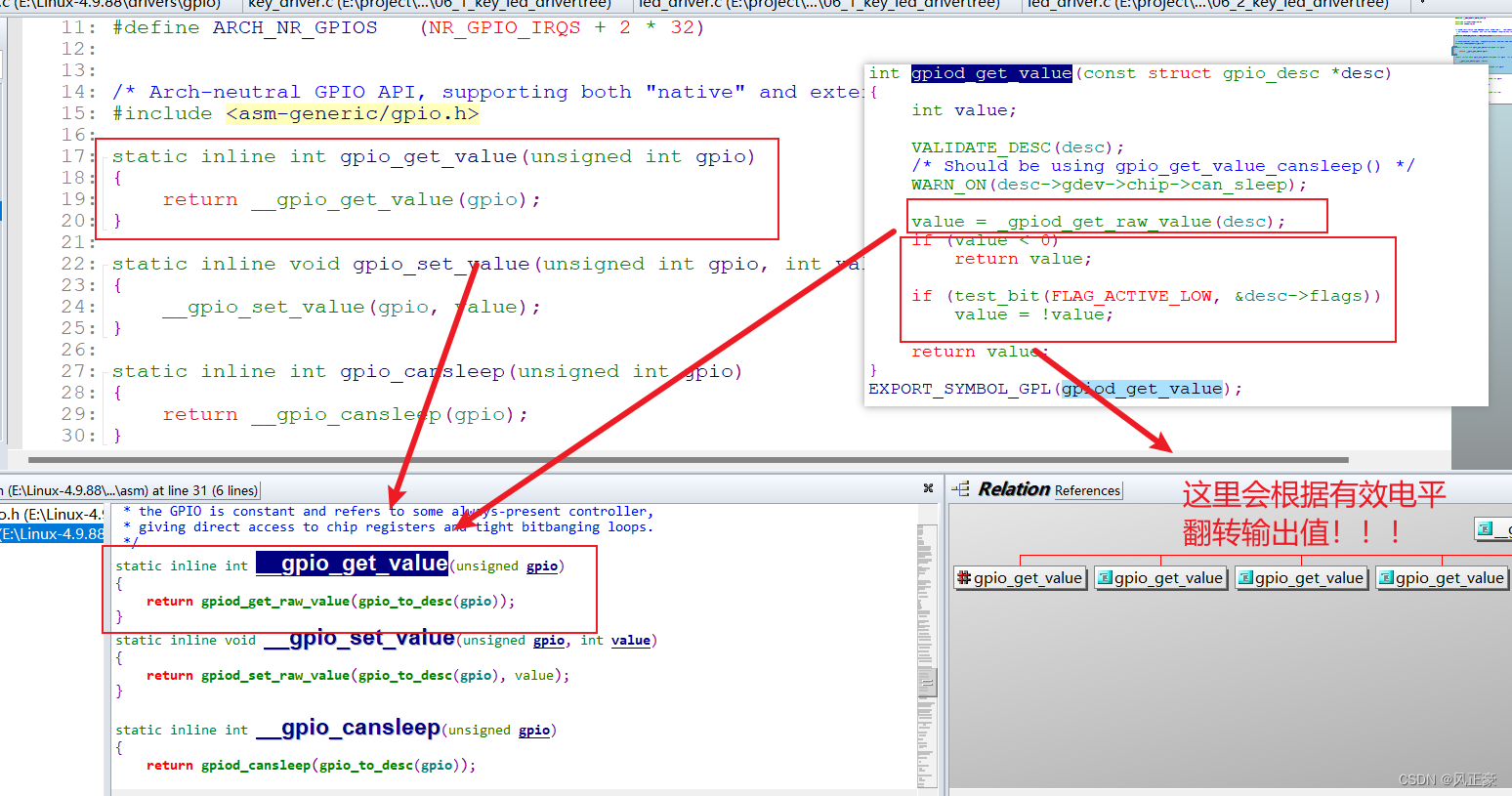
Linux驱动入门(6.2)按键驱动和LED驱动 --- 将逻辑电平与物理电平分离
前言 (1)在学习完Linux驱动入门(6)LED驱动—设备树之后,我们发现一个问题,设备树明明的gpios信息明明有三个元素gpios <&gpio5 3 GPIO_ACTIVE_LOW>; &gpio5 3 用来确定控制那个引脚…...
CentOS系统环境搭建(十四)——CentOS7.9安装elasticsearch-head
centos系统环境搭建专栏🔗点击跳转 关于node的安装请看上一篇CentOS系统环境搭建(十三)——CentOS7安装nvm,🔗点击跳转。 CentOS7.9安装elasticsearch-head 文章目录 CentOS7.9安装elasticsearch-head1.下载2.解压3.修…...
设计HTML5图像和多媒体
在网页中的文本信息直观、明了,而多媒体信息更富内涵和视觉冲击力。恰当使用不同类型的多媒体可以展示个性,突出重点,吸引用户。在HTML5之前,需要借助插件为网页添加多媒体,如Adobe Flash Player、苹果的QuickTime等。…...

基于YOLOv8模型和Caltech数据集的行人检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要 基于YOLOv8模型和Caltech数据集的行人检测系统可用于日常生活中检测与定位行人,利用深度学习算法可实现图片、视频、摄像头等方式的行人目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测算法训练数据集…...

Flutter 宽高自适应
在Flutter开发中也需要宽高自适应,手动写一个工具类,集成之后在像素后面直接使用 px或者 rpx即可。 工具类代码如下: import dart:ui;class HYSizeFit {static double screenWidth 0.0;static double screenHeight 0.0;static double phys…...
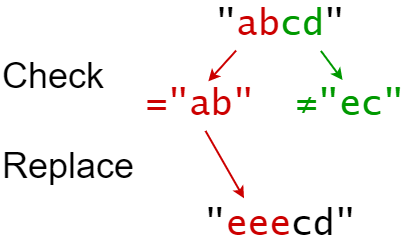
LeetCode 0833. 字符串中的查找与替换
【LetMeFly】833.字符串中的查找与替换 力扣题目链接:https://leetcode.cn/problems/find-and-replace-in-string/ 你会得到一个字符串 s (索引从 0 开始),你必须对它执行 k 个替换操作。替换操作以三个长度均为 k 的并行数组给出:indices,…...
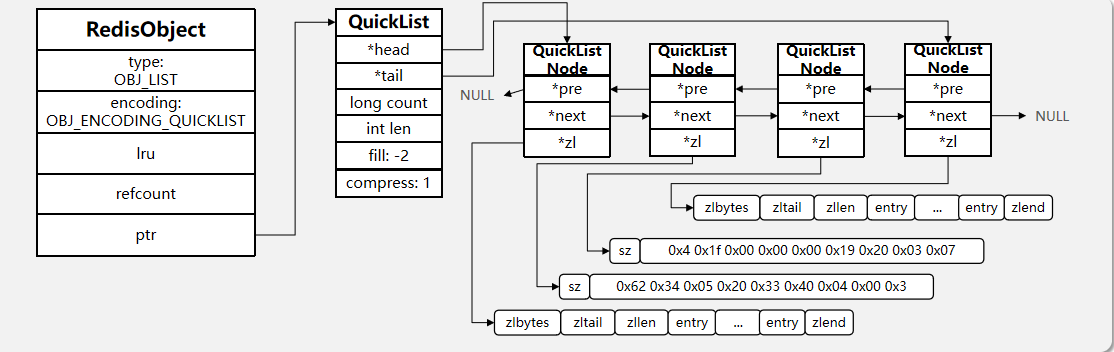
Redis对象和五种常用数据类型
Redisobject 对象 对象分为键对象和值对象 键对象一般是string类型 值对象可以是string,list,set,zset,hash q:redisobj的结构 typedef struct redisObject { //类型 unsigned type:4; //编码 unsigned encoding:4; //指向底层实现…...

常用的Elasticsearch查询DSL
1.基本查询 GET /index_name/_search {"query": {"match": {"dispatchClass": "1"}} }2.多条件查询 GET /index_name/_search {"query": {"bool": {"must": [{"match": {"createUser&…...

计算机网络笔记
TCP有连接可靠服务 TCP特点: 1.TCP是面向连接的传输层协议; 2.每条TCP连接只能有两个端点,每条TCP连接是一对一的; 3.TCP提供可靠交付,保证传送数据无差错,不丢失,不重复且有序; 4.…...
高效反编译luac文件
对于游戏开发人员,有时候希望从一些游戏apk中反编译出源代码,进行学习,但是如果你触碰到法律边缘,那么你要非常小心。 这篇文章,我针对一些用lua写客户端或者服务器的编译过的luac文件进行反编译,获取其源代码的过程。 这里我不赘述如何反编译解压apk包的过程了,只说重点…...

密码湘军,融合创新!麒麟信安参展2023商用密码大会,铸牢数据安全坚固堡垒
2023年8月9日至11日,商用密码大会在郑州国际会展中心正式开幕。本次大会由国家密码管理局指导,中国密码学会支持,郑州市人民政府、河南省密码管理局主办,以“密码赋能美好发展”为主题,旨在推进商用密码创新驱动、前沿…...
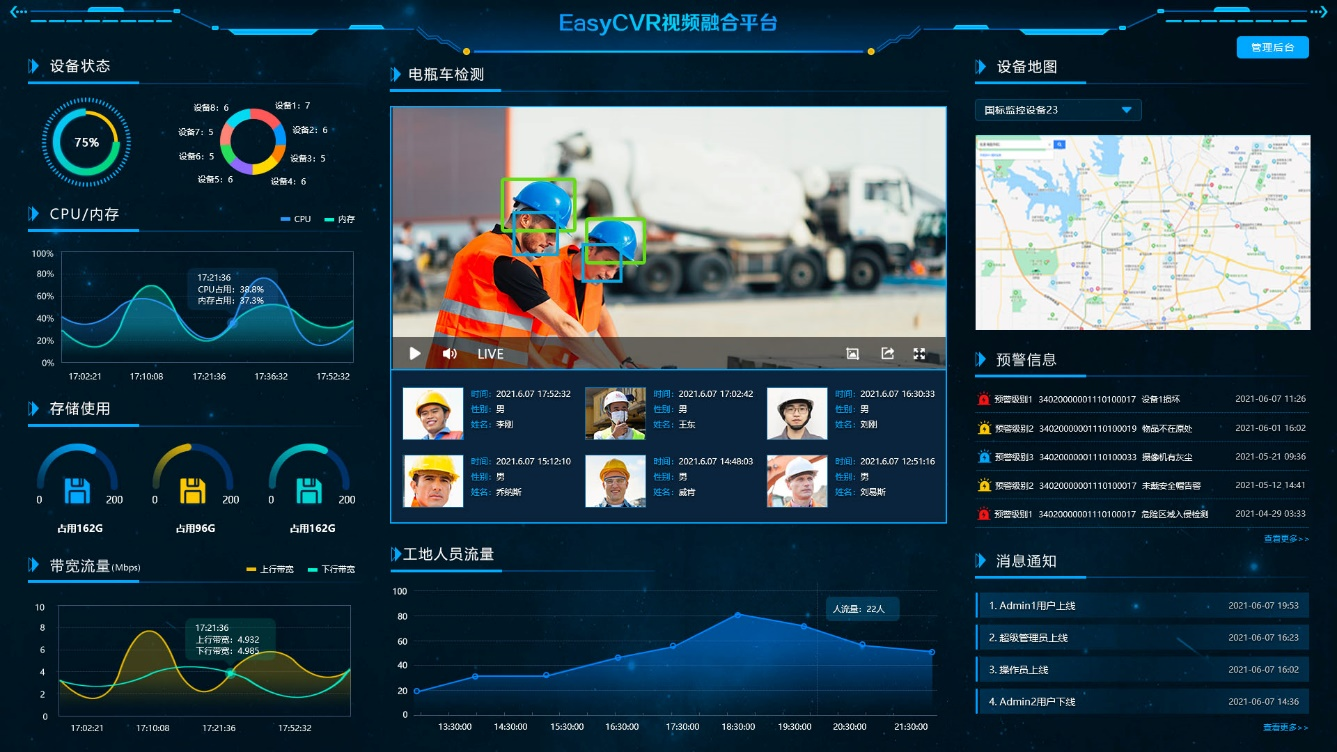
关于视频监控平台EasyCVR视频汇聚平台建设“明厨亮灶”具体实施方案以及应用
一、方案背景 近几年来,餐饮行业的食品安全、食品卫生等新闻频频发生,比如某火锅店、某网红奶茶,食材以次充好、后厨卫生被爆堪忧,种种问题引起大众关注和热议。这些负面新闻不仅让餐饮门店的品牌口碑暴跌,附带的连锁…...

区块链系统探索之路:私钥的压缩和WIF格式详解
在前面章节中,我们详细介绍了公钥的压缩,在比特币网络中,一个私钥可以对应两个地址,一个地址是由未压缩公钥所生成的地址,另一个就是由压缩公钥所创建的地址,从公钥到区块链地址的转换算法,我们…...

DiffusionDet: Diffusion Model for Object Detection
DiffusionDet: Diffusion Model for Object Detection 论文概述不同之处整体流程 论文题目:DiffusionDet: Diffusion Model for Object Detection 论文来源:arXiv preprint 2022 论文地址:https://arxiv.org/abs/2211.09788 论文代码…...

CH01_重构、第一个示例
概述 在这一章节,作者给出了一个戏剧演出团售票的示例:剧目有悲剧(tragedy)和喜剧(comedy);为了卖出更多的票,剧团则更具观众的数量来为下次演出打折扣(大致意思是这次的…...
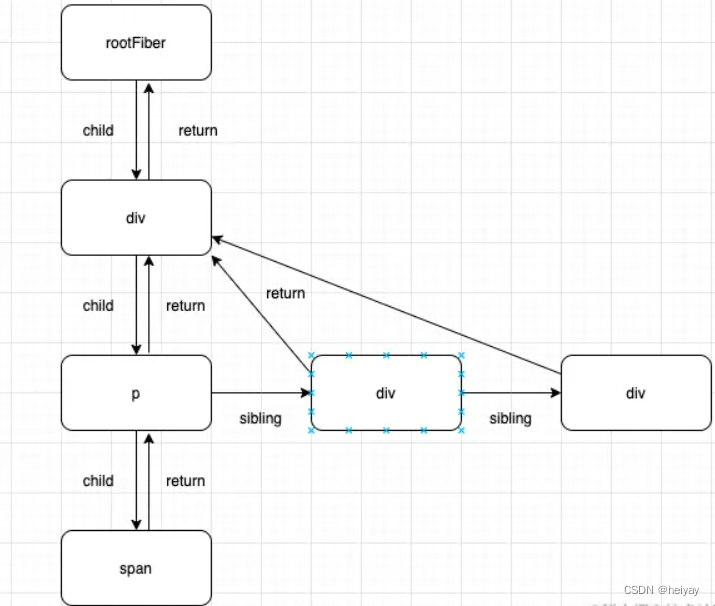
学习篇之React Fiber概念及原理
什么是React Fibber? React Fiber 是 React 框架的一种底层架构,为了改进 React 的渲染引擎,使其更加高效、灵活和可扩展。 传统上,React 使用一种称为堆栈调和递归算法来处理虚拟 DOM 的更新,这种方法在大型应用或者…...
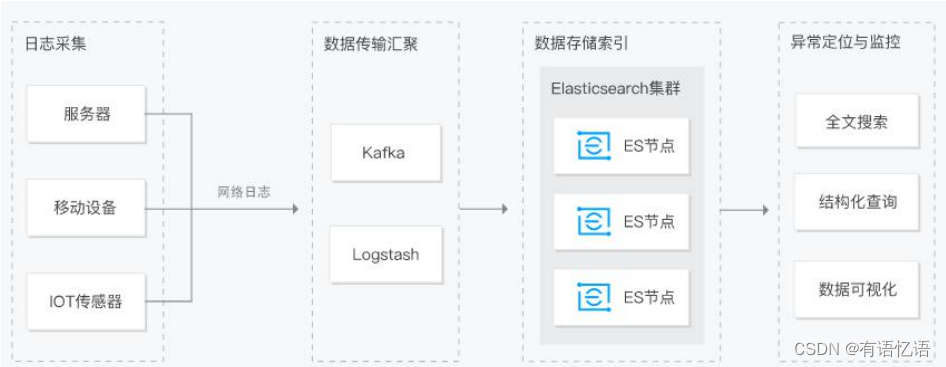
商城-学习整理-高级-全文检索-ES(九)
目录 一、ES简介1、网址2、基本概念1、Index(索引)2、Type(类型)3、Document(文档)4、倒排索引机制4.1 正向索引和倒排索引4.2 正向索引4.3 倒排索引 3、相关软件及下载地址3.1 Kibana简介3.2 logstash简介…...

无人机跟随一维高度避障场景--逻辑分析
无人机跟随一维高度避障场景--逻辑分析 1. 源由2. 视频3. 问题3.1 思维发散3.2 问题收敛 4. 图示4.1 水平模式4.2 下坡模式4.3 上坡模式4.4 碰撞分析 5. 总结5.1 一维高度避障场景5.2 业界跟随产品5.3 APM集成跟随 6. 参考资料7. 补充资料 - 大疆智能跟随7.1 炸机7.2 成功 1. 源…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...
