【力扣每日一题】1572. 矩阵对角线元素的和 8.11打卡

文章目录
- 题目
- 思路
- 代码
题目
1572. 矩阵对角线元素的和
难度: 简单
描述:
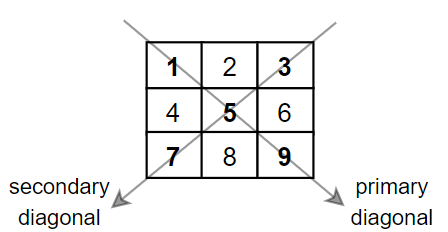
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
输入:mat = [[1,2,3],
[4,5,6],
[7,8,9]]
输出:25
解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25
请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2:
输入:mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]]
输出:8
示例3:
输入:mat = [[5]]
输出:5
提示:
- -n == mat.length == mat[i].length
- 1 <= n <= 100
- 1 <= mat[i][j] <= 100
思路
时间复杂度分析:根据分析m和n的范围,可以使用暴力法两层for循环来解题 时间复杂度为O(n^2)
同时我们观察分析,可以求出对角线的和,因此时间复杂度可以降低到O(n)
空间复杂度: O(1)
解法思路:使用一层for循环来求出对角线的和,同时根据阶数的奇偶性,奇数的话需要减一次中间值,偶数的话不用
代码
class Solution {public int diagonalSum(int[][] mat) {int m = mat.length;int n = mat[0].length;int sum =0;for(int i = 0;i<m;i++){sum += mat[i][i];}for(int j =0;j<n;j++){sum += mat[j][n-j-1];if(n % 2 == 1){sum -= mat[n/2][m/2];}return sum;}
}
相关文章:
【力扣每日一题】1572. 矩阵对角线元素的和 8.11打卡
文章目录 题目思路代码 题目 1572. 矩阵对角线元素的和 难度: 简单 描述: 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 返回合并后的二叉树。 注意…...

Wi-Fi 安全在学校中的重要性
Wi-Fi 是教育机构的基础设施,从在线家庭作业门户到虚拟教师会议,应有尽有。大多数 K-12 管理员对自己的 Wi-Fi 网络的安全性充满信心,并认为他们现有的网络安全措施已经足够。 不幸的是,这种信心往往是错误的。Wi-Fi 安全虽然经常…...

若依微服务集成CAS,实现单点登录
若依(RuoYi)微服务是一款基于Spring Cloud Alibaba开发的企业级微服务框架,采用前后端分离方式,使用了常用的微服务组件,如Feign、Nacos、Sentinel、Seata等,提供了丰富的微服务治理功能,如服务…...
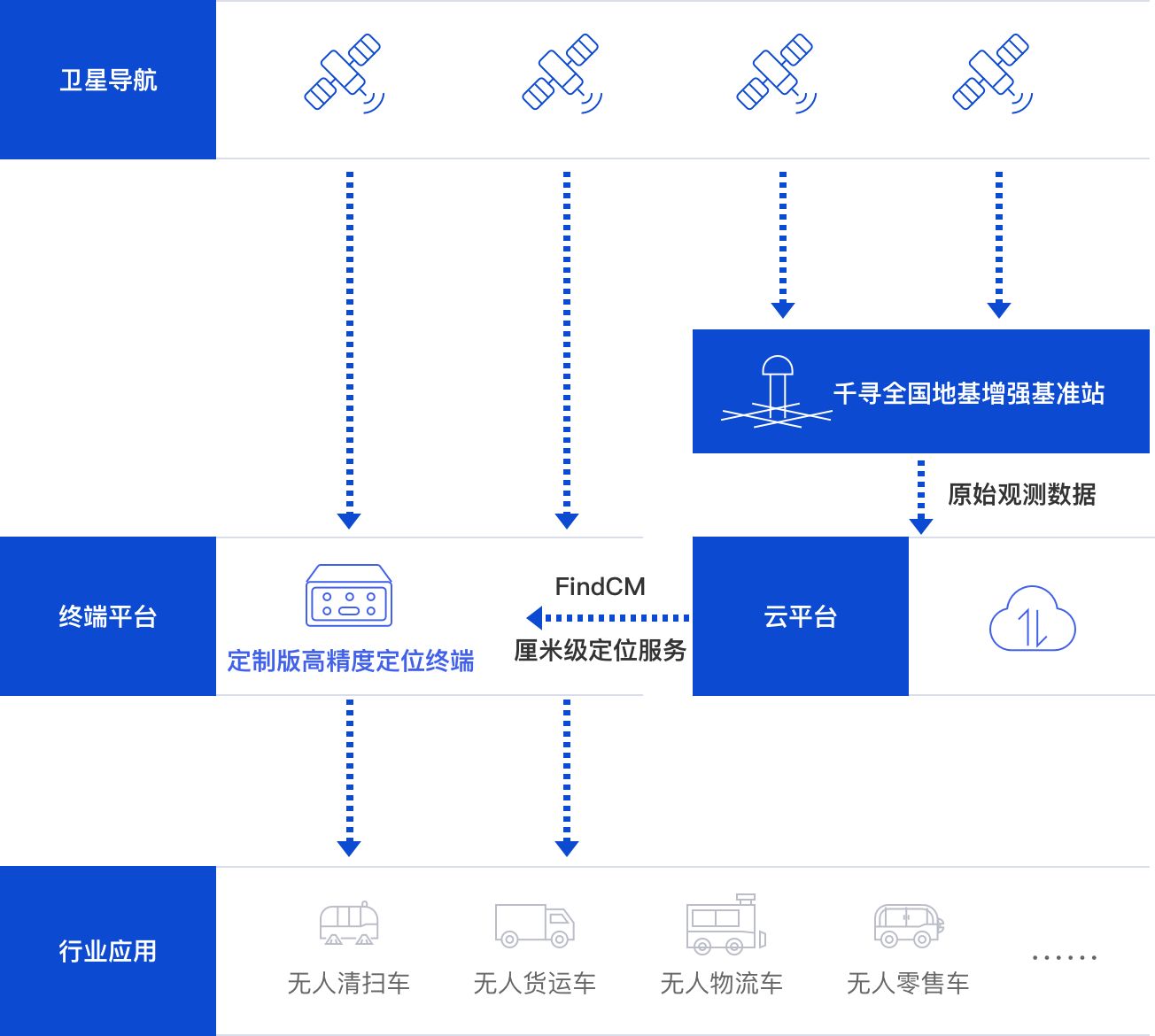
解锁园区交通新模式:园区低速自动驾驶
在当今科技飞速发展的时代,自动驾驶技术成为了备受关注的领域之一。尤其是在园区内部交通管理方面,自动驾驶技术的应用正在日益受到重视。 园区低速自动驾驶的实现需要多个技术领域的协同合作,包括自动驾驶技术、计算机视觉技术、通信技术、物…...
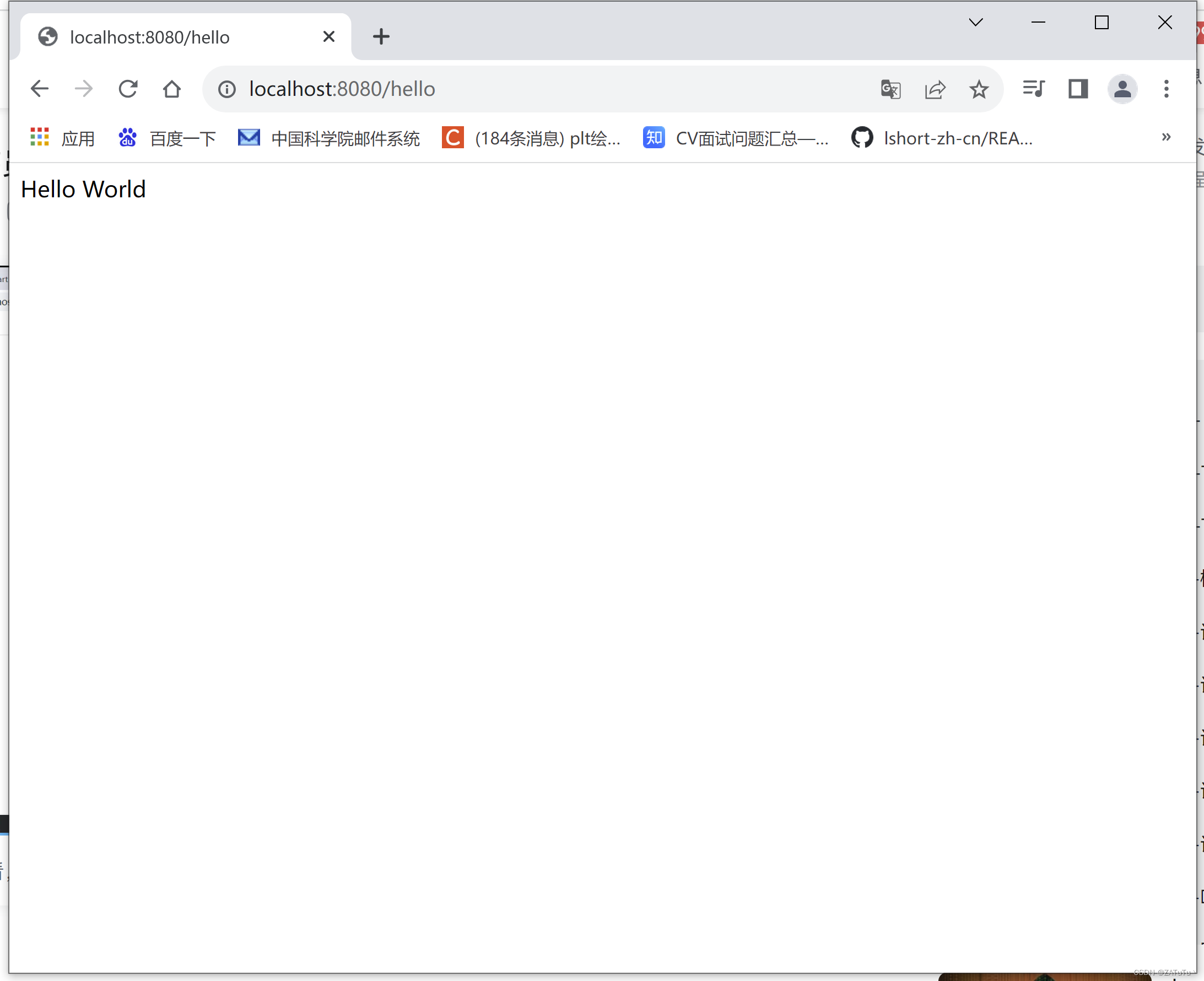
SpringBoot-Hello World
SpringBootWeb快速入门 创建Springboot工程,并勾选web开发相关依赖定义HelloController类,添加方法hello,并添加相关注释运行测试 创建新的SpringBoot项目 几个注意的点: Name:基本上不用管,会根据下面的Ar…...
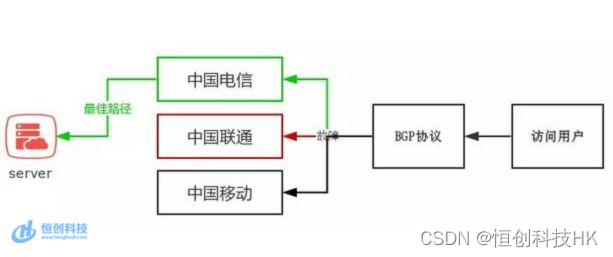
香港服务器三网直连内地线路什么意思?好用吗?
三网直连内地是指香港服务器可以直接连接中国内地的电信、联通和移动三大运营商网络,避免了中间网络干线的支持。这样可以实现直接、快速、稳定的网络访问,提高用户对网络访问的效率,减少网络访问问题和拥堵的现象。 香港服务器直连内地…...
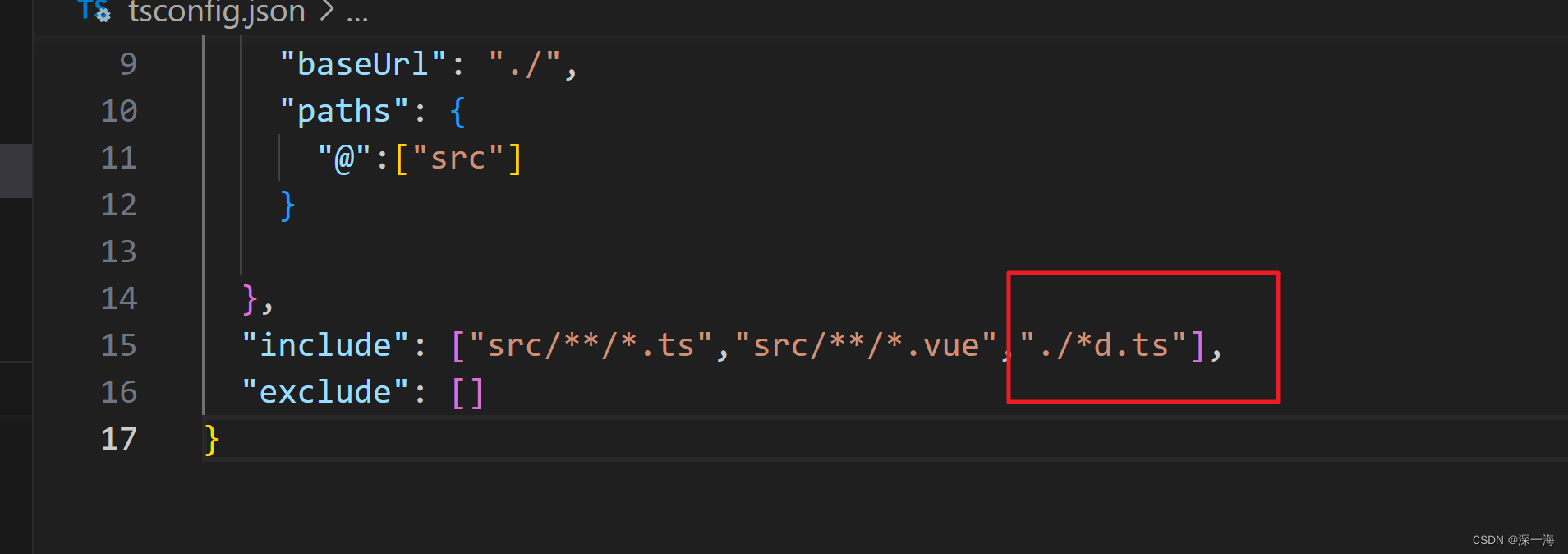
component:()=>import(“@/views/Home.vue“) 报错,ts说没有找到类型声明文件
1 没有写.vue文件的类型声明,要在env.d.ts文件中写.vue的类型声明文件 2 ts.config.josn的incluede字段中,没有把.d.ts文件的路径写对。 如果没写对,就会在项目启动的时候,找不到.d.ts文件。找不到类型声明文件...

为什么hive会出现_HIVE_DEFAULT_PARTITION分区
问题: 为什么hive表中出现_HIVE_DEFAULT_PARTITION分区? 解答: 因为在业务sql中使用的是动态分区,并且hive启用动态分区时,对于指定的分区键如果存在空值时,会对空值部分创建一个默认分区用于存储该部分…...
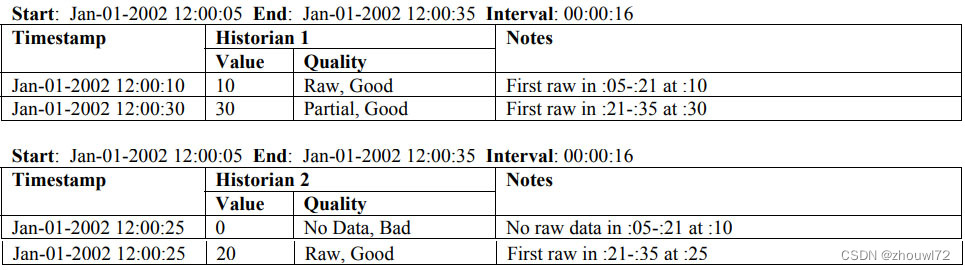
通讯协议041——全网独有的OPC HDA知识一之聚合(九)首值
本文简单介绍OPC HDA规范的基本概念,更多通信资源请登录网信智汇(wangxinzhihui.com)。 本节旨在详细说明HDA聚合的要求和性能。其目的是使HDA聚合标准化,以便HDA客户端能够可靠地预测聚合计算的结果并理解其含义。如果用户需要聚合中的自定义功能&…...
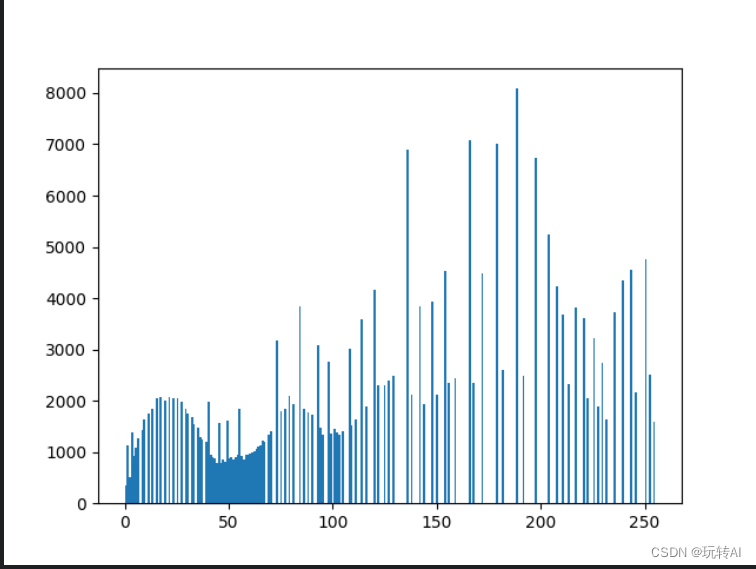
opencv进阶01-直方图的应用及示例cv2.calcHist()
直方图是什么? 直方图是一种图形表示方法,用于显示数据中各个数值或数值范围的分布情况。它将数据划分为一系列的区间(也称为“箱子”或“bin”),然后统计每个区间中数据出现的频次(或频率)。直…...

网络通信原理TCP的四次断开连接(第四十九课)
FIN:发端完成发送任务标识。用来释放一个连接。FIN=1表明此报文段的发送端的数据已经发送完毕,并要求释放连接。 SEQ:序号字段。 TCP链接中传输的数据流中每个字节都编上一个序号。序号字段的值指的是本报文段所发送的数据的第一个字节的序号。 序列号为X ACK :确认号 。 …...
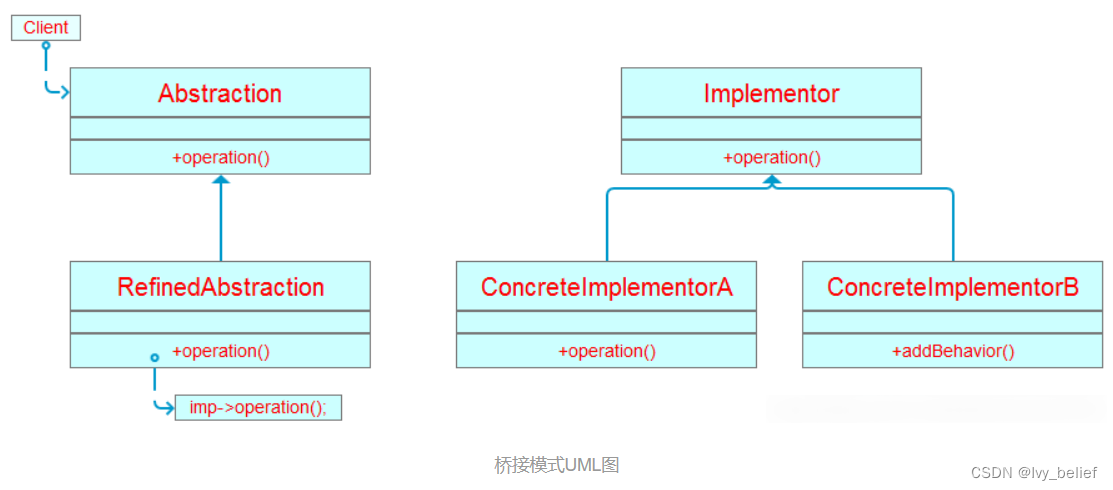
(二)结构型模式:2、桥接模式(Bridge Pattern)(C++实现示例)
目录 1、桥接模式(Bridge Pattern)含义 2、桥接模式应用场景 3、桥接模式的UML图学习 4、C实现桥接模式的示例 1、桥接模式(Bridge Pattern)含义 桥接模式是一种结构型设计模式,它将抽象部分与实现部分分离&#…...
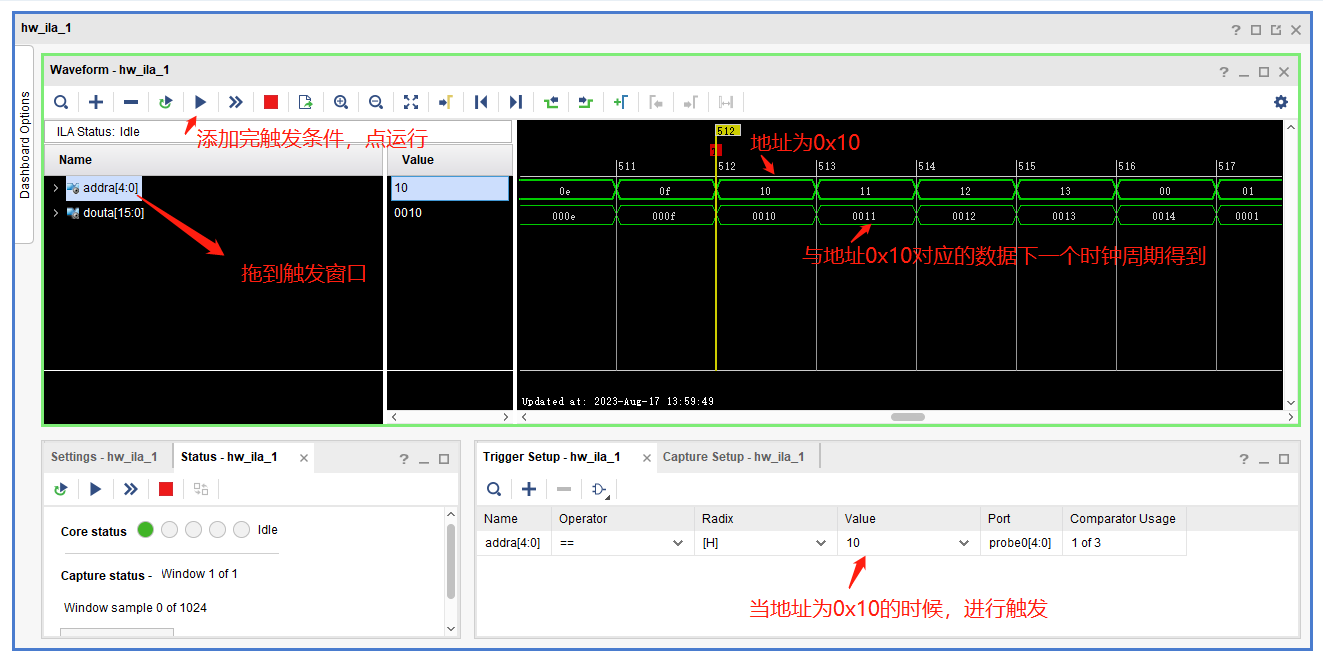
FPGA_学习_16_IP核_ROM
在寻找APD最合适的偏压的过程中,一般会用到厂商提供一条曲线,横坐标是温度的变化,纵坐标表示击穿偏压的变化,但每个产品真正的击穿偏压是有差异的。 为了能够快速的找到当前温度下真实的击穿偏压,我们可以这样做&#…...
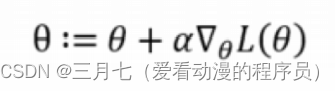
机器学习---对数几率回归
1. 逻辑回归 逻辑回归(Logistic Regression)的模型是一个非线性模型, sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函 数关系,其他的步骤,算法都是…...
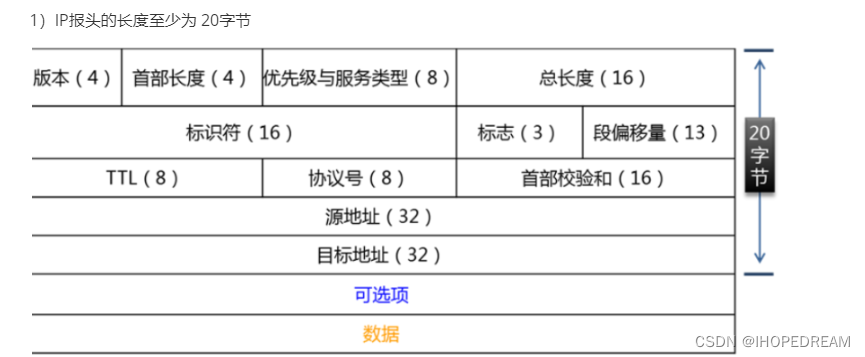
网络通信原理IP头部格式(第四十二课)
字段作用解析:1)版本: 指的IP地址的版本 (IPv4 或 IPV6)2)首部长度: 次数据包的首部长度一共是多少,没有加可选项3)优先级与服务类型:表示****数据包是否需要优选传递4)总长度: 表示的是整个数据包的大小,也就****是首部+数据5)标识符、标志、段偏移量:的作用将拆开的…...
)
Flink多流处理之join(关联)
Flink的API中只提供了join的算子,并没有left join或者right join,这里我们就介绍一下join算子的使用,其实join算子底层调用的就是coGroup,具体原理这里就不过多介绍了,如果感兴趣可以看我前面发布的文章Flink多流操作之coGroup. 数据源➜ ~ nc -lk 1111 101,A 102,B 103,C 10…...
LeetCode Top100 Liked 题单(序号34~51)
34. Find First and Last Position of Element in Sorted Array 题意:找到非递减序列中目标的开头和结尾 我的思路 用二分法把每一个数字都找到,最后返回首尾两个数 代码 Runtime12 ms Beats 33.23% Memory14 MB Beats 5.16% class Solution {…...
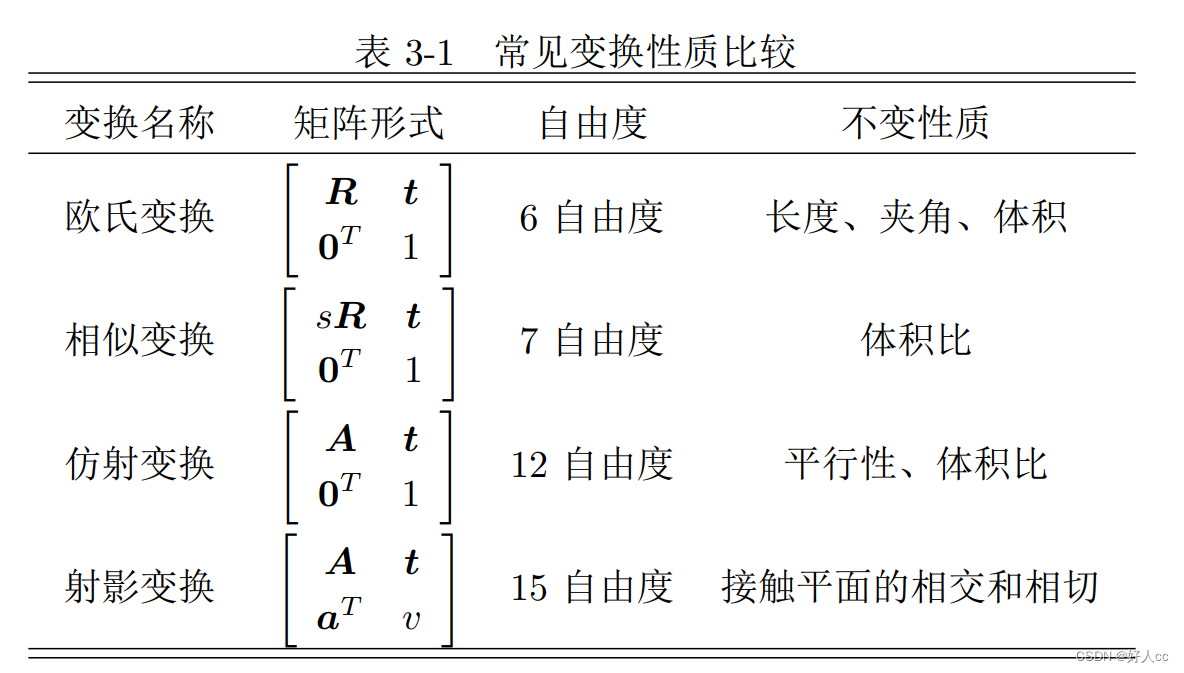
视觉slam十四讲---第一弹三维空间刚体运动
1.旋转矩阵 1.1内积 1.2外积 1.3坐标系间的欧式变换 相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会 发生变化。这种变换称为欧氏变换。 旋转矩阵:它是一个行列式为 1 的正交矩阵。 旋转矩阵为正交阵,它的逆…...
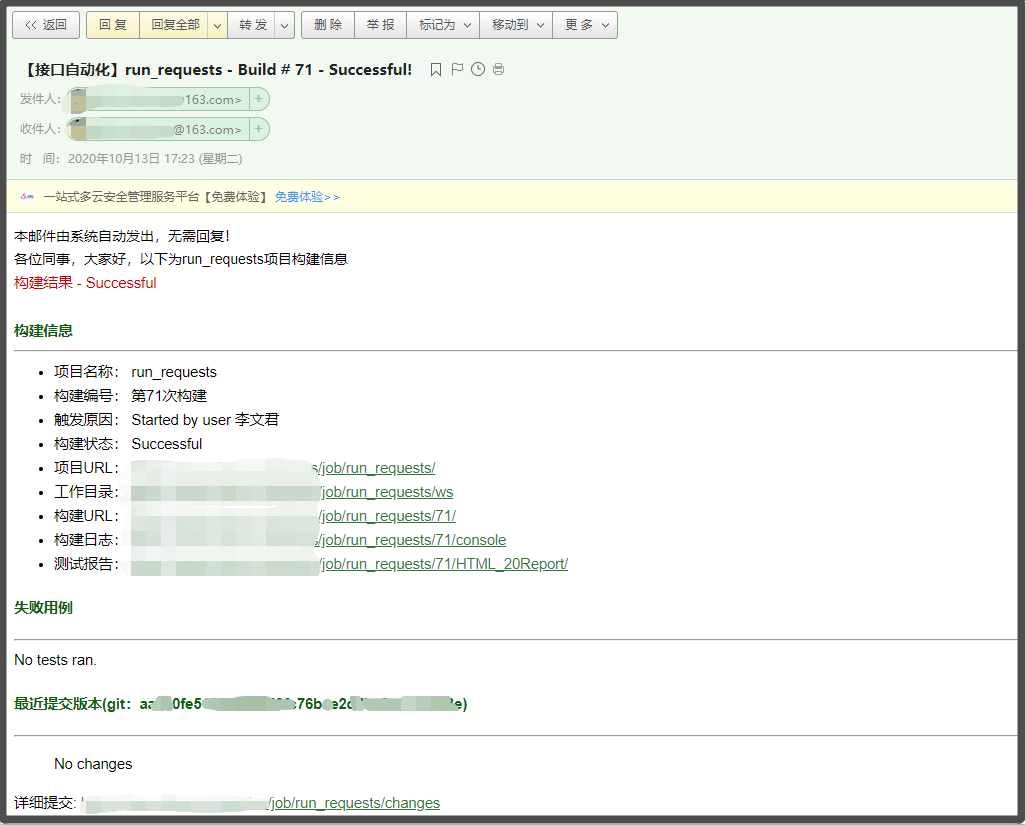
手把手教你配置Jenkins自动化邮件通知
完成基于Jenkins的持续集成部署后,自动化测试执行后,测试结果需要通知到相关人员,除了钉钉通知外我们还可以通过Email通知到对应负责人,这里记录一下测试结果通过Jenkins邮件通知的配置与部署 01、安装插件 方法1: 进…...

Arcgis连续数据的分类(求不同值域的面积)
问题描述:如果得到的一个连续的影响数值数据,但是我们想求取某一段值域的面积占比,需要进行以下操作: 1.按照数值重分类,将某段数值变成一个类别 2.栅格转矢量,再求取面积...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
