VTK 判断一个 点 是否在一个模型 stl 内部 vtk 点是否在内部 表面 寻找最近点
判断 一个点 ,判断是否在风格 stl 模型内部,或表面:
目录
1.方案一:使用vtkCellLocator FindClosestPoint 找到模型上距离给定点最近的一点,计算两点的距离 ,小于某一阈值 则认为此点在模型上;
2.方案二 使用 vtkKdTreePointLocator
3.方案三 使用 vtkSelectEnclosedPoints
1.方案一:使用vtkCellLocator FindClosestPoint 找到模型上距离给定点最近的一点,计算两点的距离 ,小于某一阈值 则认为此点在模型上;
vtkCellLocator本身是一个octree。典型的用法就是求最近的单元或者点
bool CheckPointInsidePolyData(vtkPolyData * poly, double* pt)
{bool inside=false; auto cellLocator = vtkSmartPointer<vtkCellLocator>::New();cellLocator->SetDataSet(poly);cellLocator->BuildLocator();auto assistCell = vtkSmartPointer<vtkGenericCell>::New();double closestPoint[3];//the coordinates of the closest point will be returned heredouble closestPointDist2; //the squared distance to the closest point will be returned herevtkIdType cellId; //the cell id of the cell containing the closest point will be returned hereint subId=-1;cellLocator->FindClosestPoint(point, closestPoint, assistCell, cellId, subId, closestPointDist2);if (-1!= subId&&closestPointDist2 < 0.001){return true;}return inside;
}2.方案二 使用 vtkKdTreePointLocator
但这个只能找到最新的点,还需要自己判断一下距离
官方样例:
#include <vtkIdList.h>
#include <vtkKdTreePointLocator.h>
#include <vtkNew.h>
#include <vtkPoints.h>
#include <vtkPolyData.h>int main(int, char*[])
{// Setup point coordinatesdouble x[3] = {1.0, 0.0, 0.0};double y[3] = {0.0, 1.0, 0.0};double z[3] = {0.0, 0.0, 1.0};vtkNew<vtkPoints> points;points->InsertNextPoint(x);points->InsertNextPoint(y);points->InsertNextPoint(z);vtkNew<vtkPolyData> polydata;polydata->SetPoints(points);// Create the treevtkNew<vtkKdTreePointLocator> kDTree;kDTree->SetDataSet(polydata);kDTree->BuildLocator();double testPoint[3] = {2.0, 0.0, 0.0};// Find the closest points to TestPointvtkIdType iD = kDTree->FindClosestPoint(testPoint);std::cout << "The closest point is point " << iD << std::endl;// Get the coordinates of the closest pointdouble closestPoint[3];kDTree->GetDataSet()->GetPoint(iD, closestPoint);std::cout << "Coordinates: " << closestPoint[0] << " " << closestPoint[1]<< " " << closestPoint[2] << std::endl;return EXIT_SUCCESS;
}3.方案三 使用 vtkSelectEnclosedPoints
vtkSelectEnclosedPoints类可以判断标记点是否在封闭表面内。
vtkSelectEnclosedPoints是一个Filter,它计算所有输入点以确定它们是否位于封闭曲面中。过滤器生成一个(0,1)掩码(以vtkDataArray的形式),指示点是在提供的曲面的外部(掩码值=0)还是内部(掩码值=1)(输出vtkDataArray的名称是“SelectedPoints”。)
运行过滤器后,可以通过调用IsInside(ptId)方法来查询点是否在内部/外部。
样例:判断三个点是否在立方体内
注意:在立方体边上的点,不属于在立方体内部;

CODE
#include <vtkVersion.h>
#include <vtkPolyData.h>
#include <vtkPointData.h>
#include <vtkCubeSource.h>
#include <vtkSmartPointer.h>
#include <vtkSelectEnclosedPoints.h>
#include <vtkIntArray.h>
#include <vtkDataArray.h>
#include <vtkProperty.h>
#include <vtkPolyDataMapper.h>
#include <vtkActor.h>
#include <vtkRenderWindow.h>
#include <vtkRenderer.h>
#include <vtkRenderWindowInteractor.h>int main(int, char*[])
{vtkNew<vtkCubeSource> cubeSource;cubeSource->Update();vtkPolyData* cube = cubeSource->GetOutput();double testInside[3] = { 0.0, 0.0, 0.0 };double testOutside[3] = { 0.7, 0.0, 0.0 };double testBorderOutside[3] = { 0.5, 0.0, 0.0 };vtkNew<vtkPoints> points;points->InsertNextPoint(testInside);points->InsertNextPoint(testOutside);points->InsertNextPoint(testBorderOutside);vtkNew<vtkPolyData> pointsPolydata;pointsPolydata->SetPoints(points);//Points inside testvtkNew<vtkSelectEnclosedPoints> selectEnclosedPoints;selectEnclosedPoints->SetInputData(pointsPolydata);selectEnclosedPoints->SetSurfaceData(cube);selectEnclosedPoints->Update();for (unsigned int i = 0; i < 3; i++) {std::cout << "Point " << i << ": " << selectEnclosedPoints->IsInside(i) << std::endl;}vtkDataArray* insideArray = vtkDataArray::SafeDownCast(selectEnclosedPoints->GetOutput()->GetPointData()->GetArray("SelectedPoints"));for (vtkIdType i = 0; i < insideArray->GetNumberOfTuples(); i++) {std::cout << i << " : " << insideArray->GetComponent(i, 0) << std::endl;}//Cube mapper, actorvtkNew<vtkPolyDataMapper> cubeMapper;cubeMapper->SetInputConnection(cubeSource->GetOutputPort());vtkNew<vtkActor> cubeActor;cubeActor->SetMapper(cubeMapper);cubeActor->GetProperty()->SetOpacity(0.5);//First, apply vtkVertexGlyphFilter to make cells around points, vtk only render cells.vtkNew<vtkVertexGlyphFilter> vertexGlyphFilter;vertexGlyphFilter->AddInputData(pointsPolydata);vertexGlyphFilter->Update();vtkNew<vtkPolyDataMapper> pointsMapper;pointsMapper->SetInputConnection(vertexGlyphFilter->GetOutputPort());vtkNew<vtkActor> pointsActor;pointsActor->SetMapper(pointsMapper);pointsActor->GetProperty()->SetPointSize(5); pointsActor->GetProperty()->SetColor(1.0, 0.0, 0);//Create a renderer, render window, and interactorvtkNew<vtkRenderer> renderer;vtkNew<vtkRenderWindow> renderWindow;renderWindow->AddRenderer(renderer);vtkNew<vtkRenderWindowInteractor> renderWindowInteractor;renderWindowInteractor->SetRenderWindow(renderWindow);// Add the actor to the scenerenderer->AddActor(cubeActor);renderer->AddActor(pointsActor);renderer->SetBackground(.0, 1, .0);renderWindow->Render();renderWindowInteractor->Start();return EXIT_SUCCESS;
}输出:
Point 0: 1
Point 1: 0
Point 2: 0
0 : 1
1 : 0
2 : 0
相关文章:

VTK 判断一个 点 是否在一个模型 stl 内部 vtk 点是否在内部 表面 寻找最近点
判断 一个点 ,判断是否在风格 stl 模型内部,或表面: 目录 1.方案一:使用vtkCellLocator FindClosestPoint 找到模型上距离给定点最近的一点,计算两点的距离 ,小于某一阈值 则认为此点在模型上; 2.方案二…...
【数据结构OJ题】链表的回文结构
原题链接:https://www.nowcoder.com/practice/d281619e4b3e4a60a2cc66ea32855bfa?tpId49&&tqId29370&rp1&ru/activity/oj&qru/ta/2016test/question-ranking 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 在做这道…...
Nginx常见的三个漏洞
目录 $uri导致的CRLF注入漏洞 两种常见场景 表示uri的三个变量 案例 目录穿越漏洞 案例 Http Header被覆盖的问题 案例 $uri导致的CRLF注入漏洞 两种常见场景 用户访问http://example.com/aabbcc,自动跳转到https://example.com/aabbcc 用户访问http://exa…...
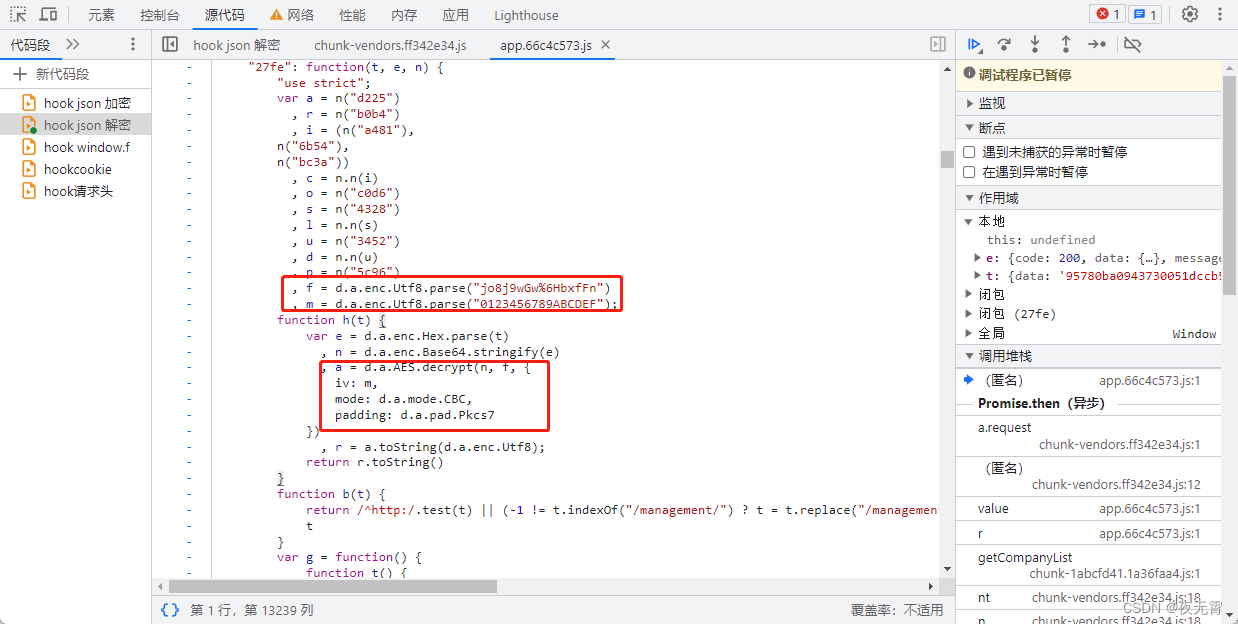
爬虫逆向实战(十六)--某建筑市场平台
一、数据接口分析 主页地址:某建筑市场平台 1、抓包 通过抓包可以发现数据接口是list 2、判断是否有加密参数 请求参数是否加密? 无请求头是否加密? 无响应是否加密? 通过查看“响应”模块可以发现,返回的响应是…...

用Python做一个滑雪小游戏
游戏是让人娱乐和放松的好方式,而编写和玩自己的游戏则是一种特别有趣的体验。在本文中,我们将使用Python和pygame库来创建一个简单的滑雪小游戏。通过这个小游戏项目,我们将学习如何使用Python编程语言来制作自己的游戏,并且享受…...
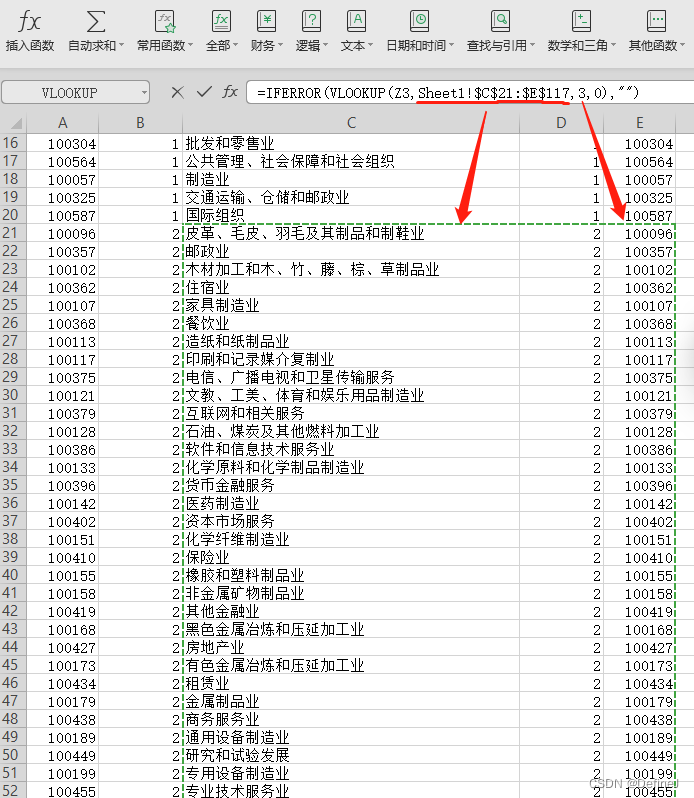
EXCEL按列查找,最终返回该列所需查询序列所对应的值,VLOOKUP函数
EXCEL按列查找,最终返回该列所需查询序列所对应的值 示例:国标行业分类汉字,匹配id 使用VLOOKUP函数 第一参数:拿去查询的值。 第二参数:匹配的数据。 Ps:Sheet1!$C 21 : 21: 21:E 117 ,需要…...

java编译报错,get方法报错
java编译报错,get方法报错 处理方式: 在空间中,将 buid 文件夹删除 再不行的话,重启电脑,删除各种缓存 试试...

可以降低CPU负载的网络传输技术——LSO
LSO 是个啥? Large Send Offload(LSO)是一种网络传输协议技术,旨在提高网络传输的性能和效率。它通过将大型数据包拆分成小型数据包,降低网络传输负载,提高传输速度。 在传统的网络传输协议中,…...

[管理与领导-25]:IT基层管理者 - 团队管理 - 如何留人, 如何留住关键人才
目录 一、离职前的五大信号,你读懂了吗? 二、员工为什么会离职 三、如何留住关键人才 一、离职前的五大信号,你读懂了吗? 离职前的信号是指员工可能在准备离职之前表现出的一些迹象或行为。 这些信号可以帮助雇主或同事们察觉…...
之 Jedis)
【Redis】Redis 的学习教程(二)之 Jedis
仅仅知道 Redis 服务端的操作知识,还是远远不够的,如果想要真正在项目中得到应用,我们还需要一个 Redis 的客户端,然后将其集成到项目中,让程序自动根据我们的业务需要自动处理。 基于 Redis 开放的通信协议ÿ…...

VB+SQL银行设备管理系统设计与实现
摘要 随着银行卡的普及,很多地方安装了大量的存款机、取款机和POS机等银行自助设备。银行设备管理系统可以有效的记录银行设备的安装和使用情况,规范对自助设备的管理,从而为用户提供更加稳定和优质的服务。 本文介绍了银行设备管理系统的设计和开发过程,详细阐述了整个应…...
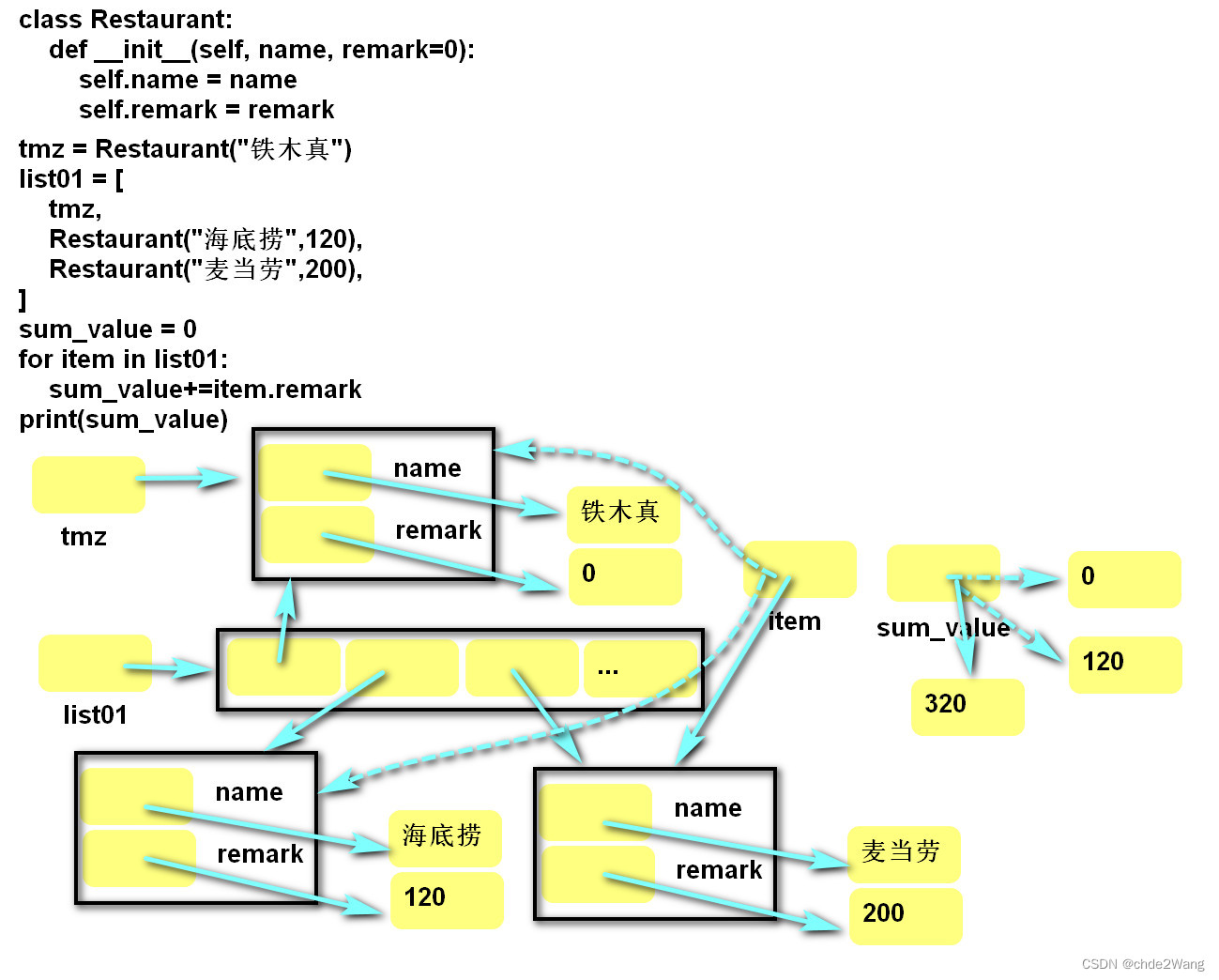
Python系统学习1-9-类一之类语法
一、类之初印象 1、类就是空表格,将变量(列名)和函数(行为)结合起来 2、创建对象,表达具体行 3、创建类就是创建数据的模板 --操作数据时有提示 --还能再组合数据的行为 --结构更加清晰 4、类的内存分配…...

PHP“深入浅出”淘宝商品详情数据接口获取方法,淘宝API申请指南
获取淘宝商品详情数据的方法如下: 确定监控对象,通常是与自己店铺的商品相似的竞品,通过在淘宝商品详情页的URL中获取商品ID,进而获取商品的详情数据。通过API接口获取商品详情数据,申请开发者账号并获取授权访问&…...

线性代数再回顾
最近,在深度学习线性代数,之前大一的时候学过线性代数,但那纯属于是应试用的,考试一考完,啥都忘了,也说出不出个所以然,所以,在B站的MIT的线性代数以及3blue1brown线性代数的本质中去…...
(白帽黑客)自学笔记
一、前言: 1.这是一条坚持的道路,三分钟的热情可以放弃往下看了. 2.多练多想,不要离开了教程什么都不会了.最好看完教程自己独立完成技术方面的开发. 3.有时多 google,baidu,我们往往都遇不到好心的大神,谁会无聊天天给你做解答. 4.遇到实在搞不懂的,可以先放放,以…...

基于长短期神经网络的客流量预测,基于长短期神经网络的超短期客流量预测,lstm详细原理
目录 背影 摘要 LSTM的基本定义 LSTM实现的步骤 基于长短期神经网络LSTM的客流量预测 完整代码: 基于长短期神经网络LSTM的公交站客流量预测资源-CSDN文库 https://download.csdn.net/download/abc991835105/88184734 效果图 结果分析 展望 参考论文 背影 碳排放越来越受到重…...

前端文件下载通用方法
zip文件和xlsx文件 import axios from axios import { getToken } from /utils/authconst mimeMap {xlsx: application/vnd.openxmlformats-officedocument.spreadsheetml.sheet,zip: application/zip }const baseUrl process.env.VUE_APP_BASE_API // zip下载 export functi…...

htmlCSS-----案例展示
目录 前言 作品效果 html代码 CSS代码 图片资源 前言 在学习html过程中我们要试着去写写一些案例,通过这些案例让我们更加熟悉代码以及丰富我们的经验,下面是我个人写的一个案例,代码和图片也给出了大家,你们可以参考参考。…...

Android进阶之路 - 去除EditText内边距
正如题名,在Android中的EditText是自带内边距的,常规而言设置背景为null即可,但是因为使用了并不熟悉的声明式框架,本是几分钟解决的事儿,却花费了小半天~ 其实这只是一个很简单的小需求,不想却遇到了一些小…...
ModStartCMS v7.0.0 多语言开发优化,多个常用组件升级
ModStart 是一个基于 Laravel 模块化极速开发框架。模块市场拥有丰富的功能应用,支持后台一键快速安装,让开发者能快的实现业务功能开发。 系统完全开源,基于 Apache 2.0 开源协议,免费且不限制商业使用。 功能特性 丰富的模块市…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
