数学建模(二)线性规划
课程推荐:6 线性规划模型基本原理与编程实现_哔哩哔哩_bilibili
目录
一、线性规划的实例与定义
1.1 线性规划的实例
1.2 线性规划的定义
1.3 最优解
1.4 线性规划的Mathlab标准形式
1.5 使用linprog函数
二、线性规划模型建模实战与代码
2.1 问题提出
2.2 基本假设
2.3 模型的分析与建立
2.3.1 模型分析
2.3.2 建立模型
2.3.3 多目标线性规划模型转化为单目标线性规划模型——制定界限
2.3.4 求解
在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支:数学规划。而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。
一、线性规划的实例与定义
1.1 线性规划的实例
例:某机床厂生产甲、乙两种机床,每台销售后的利润分别为4千元与3千元。生产甲机床需用A、B机器加工,加工时间分别为每台 2小时和1小时;生产乙机床需用A、B、C三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
上述问题的数学模型:设该厂生产x1台甲机床和x2乙机床时总利润z最大,则x1,x2应满足:
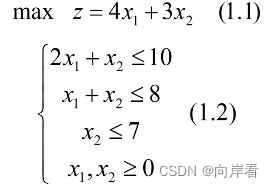
以上便是一个线性规划问题的数学模型,其中变量x1,x2称之为决策变量,(1.1)式被称为问题的目标函数,(1.2)中的几个不等式是问题的约束条件,记为s.t.(即subject to)。
1.2 线性规划的定义
目标函数及约束条件均为线性函数,故被称为线性规划问题。线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
1.3 最优解
满足约束条件的解x=[x,,L ,xI',称为线性规划问题的可行解,而使目标函数达到最大值的可行解叫最优解。
1.4 线性规划的Mathlab标准形式
线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便,Matlab中规定线性规划的标准形式:
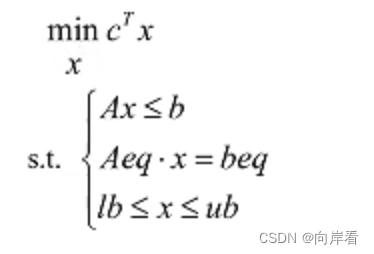
其中c和x为n维列向量,A、Aeq为适当维数的矩阵,b、beq为适当维数的列向量。
Matlab中求解线性规划的命令为:
Matlab中的linprog函数是一个线性规划求解器,可以用于求解线性规划问题。使用条件:满足Mathlab线性规划标准形式。
[x,fval] = linprog(c,A,b)
[x,fval] = linprog(c,A,b,Aeq,beq)
[x,fval] = linprog(c,A,b,Aeq,beq,lb,ub)
其中,x返回的是决策向量的取值,fval返回的是目标函数的最优值,c为价值向量,A,b对应的是线性不等式约束,Aeq,beq对应的是线性等式约束,lb和ub分别对应的是决策向量的下界向量和上界向量。
1.5 使用linprog函数

求解的Matlab程序如下:
f=[-2;-3;5];
a=[-2,5,-1;1,3,1]; b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x, y=-y1. 目标函数中求max时,将目标函数的系数全部取反,即可看作求min,代入linprog函数,求得目标函数的最优值再取反回来,便得到了求max时目标函数的最优值(y)。这时,决策向量(x)的取值正对应着求max时目标函数的最优值,所以不变。
2. 约束条件中的不等号为大于号时,系数全部取反,代入linprog函数即可。
二、线性规划模型建模实战与代码
2.1 问题提出
市场上有n种资产
(i= 1,2,L ,n)可以选择,现用数额为M的相当大的资金作一个时期的投资。这n种资产在这一时期内购买
的平均收益率为
,风险损失率为
,投资越分散,总的风险越少,总体风险可用投资的
中最大的一个风险来度量。
购买时要付交易费,费率为
,当购买额不超过给定值
时,交易费按购买
计算。另外,假定同期银行存款利率是
,既无交易费又无风险(
= 5%)。
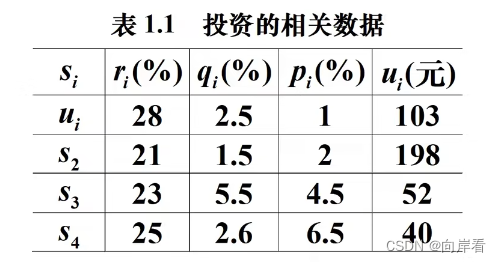
已知n=4时相关数据如表1.1。
试给该公司设计一种投资组合方案,即用给定资金M,有选择地购买若干种资产或存银行生息,使净收益尽可能大,使总体风险尽可能小。
2.2 基本假设
- (1)投资数额M相当大,为了便于计算,假设M=1。
- (2)投资越分散,总的风险越小。
- (3)总体风险用投资项目
中最大的一个风险来度量。
- (4)n+1 种
资产之间是相互独立的。其中s0表示存入银行的资产。
- (5)在投资的这一时期内,
,
,
为定值,不受意外因素影响。
- (6)净收益和总体风险只受
,
,
影响,不受其它因素干扰。
2.3 模型的分析与建立
2.3.1 模型分析
- 1. 首先,我们要明确两个目标,即收益最大和风险最小,因此这是一个多目标规划模型。
- 2. 总体风险用所投资的
中最大的一个风险来衡量,即
- 3. 购买
(i= 1,L ,n) 所付交易费是一个分段函数,即
![]()
而所给的定值 (单位:元)相对总投资M很小,
更小可以忽略不计,这样购买
的净收益可以简化为
。
2.3.2 建立模型
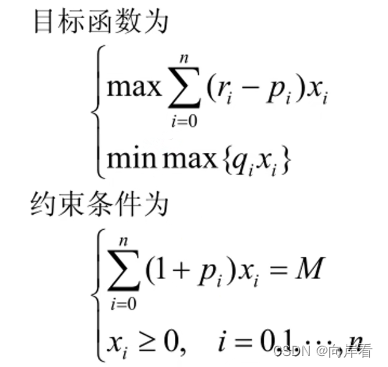
其中, 表示投资项目
的资金,i= 0,1,…,n;x0表示存入银行的资产。约束条件表示总资金投入必须等于M,投资项目
的资金必须大于等于0。
2.3.3 多目标线性规划模型转化为单目标线性规划模型——制定界限
方案一:固定风险水平,优化收益
在实际投资中,投资者承受风险的程度不一样, 若给定风险一个界限a,使最大的一个风险,可找到相应的投资方案。这样把多目标规划变成一个目标的线性规划。
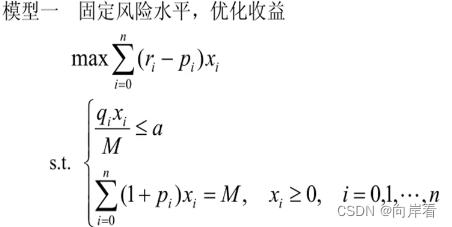
方案二:固定盈利水平,极小化最大风险
给定收益一个界限k。
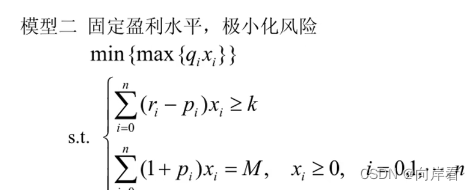
方案三:设置投资偏好系数
投资者在权衡资产风险和预期收益两方面时,希望选择一个令自己满意的投资组合。因此对风险、收益分别赋予权重s (0<s≤1)和1-s,s称为投资偏好系数。
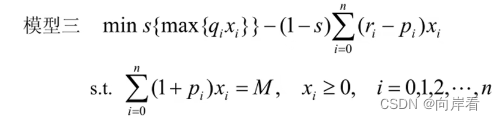
2.3.4 求解
模型一:

由于a是任意给定的风险度,没有一个确定的准则,不同的投资者有不同的风险度。我们从a= 0开始,以步长 = 0.001进行循环搜索,编制程序如下:
clc,clear
a=0;hold on
while a<0.05c=[-0.05,-0.27,-0.19,-0.185,-0.185];A=[zeros(4,1 ),diag([0.025,0.015,0.055,0.026])];b=a*ones(4,1);Aeq=[1,1.01,1.02,1.045,1.065];beq=1; LB= zeros(5,1);[x,Q]=linprog(C,A,b,Aeq,beq,LB);Q=-Q; plot(a,Q,'*k');a=a+0.001;
end
xlabel('a'),ylabel('Q')
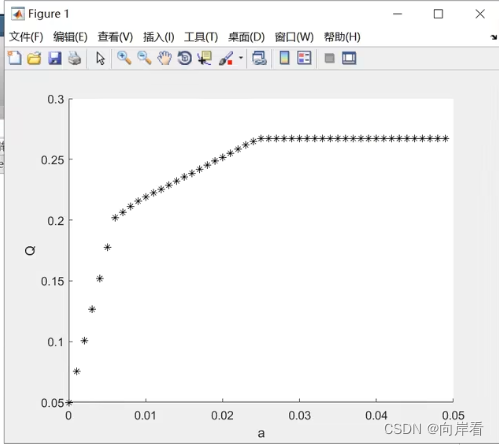
可以看出,在a=0.006附近有一个转折点,在这一点左边,风险增加很少时,利润增长很快。在这一点右边,风险增加很大时,利润增长很缓慢,所以对于风险和收益没有特殊偏好的投资者来说,应该选择曲线的转折点作为最优投资组合,所对应投资方案为风险度a= 0.006,收益Q=0.2019,x0=0,x1= 0.24,x1= 0.4,x3= 0.1091,x4= 0.2212。
相关文章:

数学建模(二)线性规划
课程推荐:6 线性规划模型基本原理与编程实现_哔哩哔哩_bilibili 目录 一、线性规划的实例与定义 1.1 线性规划的实例 1.2 线性规划的定义 1.3 最优解 1.4 线性规划的Mathlab标准形式 1.5 使用linprog函数 二、线性规划模型建模实战与代码 2.1 问题提出 2.2…...
小白到运维工程师自学之路 第七十三集 (kubernetes应用部署)
一、安装部署 1、以Deployment YAML方式创建Nginx服务 这个yaml文件在网上可以下载 cat nginx-deployment.yaml apiVersion: apps/v1 #apiVersion是当前配置格式的版本 kind: Deployment #kind是要创建的资源类型,这里是Deploymnet metadata: #metadata是该资源…...

联合仿真 ADAMS 和 SIMULINK步骤
1、把 control 中的 ball_beam 文件 copy 到另外一个文件夹下, 同时设置adams和matlab的默认路径即为ball_beam文件夹, 这样可以省略很多不必要的麻烦! 2、用 aview 打开 ball_beam.cmd 文件,先试试仿真一下,可 以看到…...
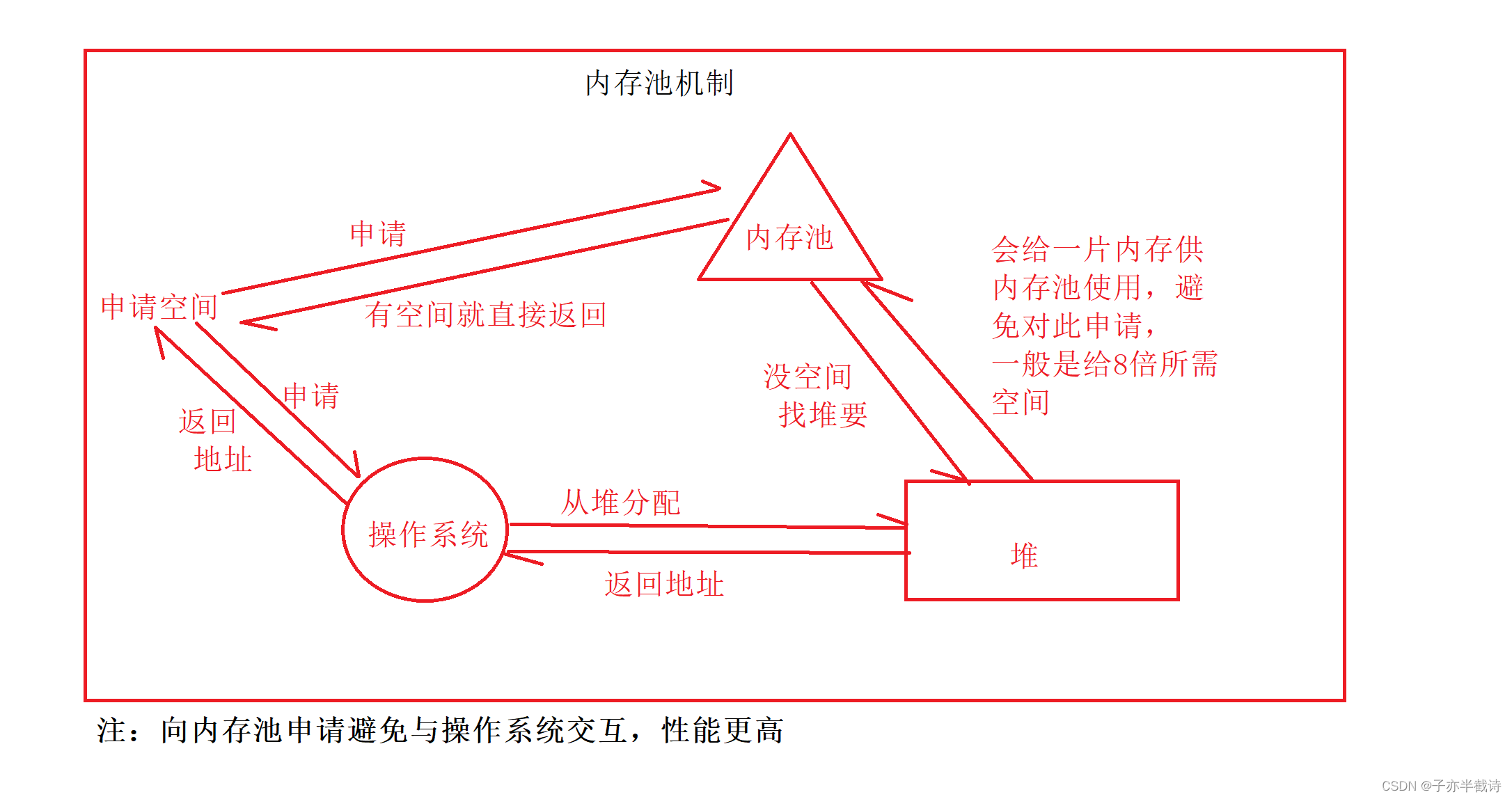
【C++精华铺】7.C++内存管理
目录 1. C语言动态内存管理 2. C内存管理方式 2.1 new/delete和new T[]/delete[] 2.1.1 操作内置类型 2.1.2 操作自定义类型 2.2 new/delete和new T[]/delete[]的原理 2.2.1 原理 2.2.2 operator new和operator delete 2.2.3 new T[]的特殊处理(可以…...

牛客网华为OD前端岗位,面试题库练习记录02
题目一 删除字符串中出现次数最少的字符(HJ23) JavaScript Node ACM 模式 const rl require("readline").createInterface({ input: process.stdin }); var iter rl[Symbol.asyncIterator](); const readline async () > (await iter.next()).value;void (asyn…...

数据库动态增删数据,导致分页查询数据出现重复或遗漏的问题分析及解决方案
一、问题分析 1. 请求数据 一般情况下,为了减少服务器的压力或方便展示,前端通过分页方式来请求数据,调用 API 接口时会带上参数 page 与 pageSize。例如请求某个班级的学生数据,获取第一页的 10 个学生的数据 ,假设按…...

神经网络基础-神经网络补充概念-44-minibatch梯度下降法
概念 小批量梯度下降法(Mini-Batch Gradient Descent)是梯度下降法的一种变体,它结合了批量梯度下降(Batch Gradient Descent)和随机梯度下降(Stochastic Gradient Descent)的优点。在小批量梯…...
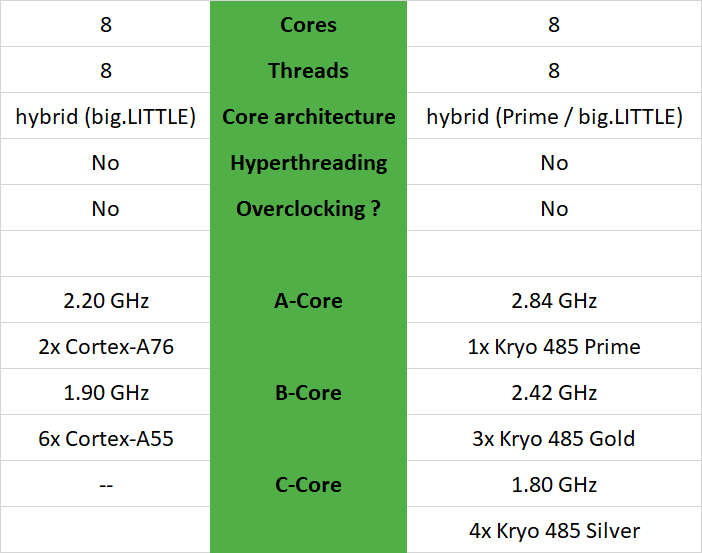
比较海思麒麟810与高通骁龙855的优劣
海思麒麟810与高通骁龙855可以从以下几方面进行比较: 一、CPU比较 海思麒麟810还是高通骁龙855——哪个处理器更快?在这个比较中,我们观察了差异,并分析了这两个CPU中哪一个更好。我们比较了技术数据和基准测试结果。 海思麒麟810有8个内核和8个线程,时钟最高频率为2.2…...

计算机机房的管理
1 电源问题 不稳定的电源对电脑的使用寿命是一个极大的威胁,特别是对于机房来说危害 性更大。为此,学校要添置必要的稳压器,设置其正常供电的电压为 220 伏、电流 为 l6 安对电脑室供电。如有电压发生偏差,要及时检查供电情况&…...
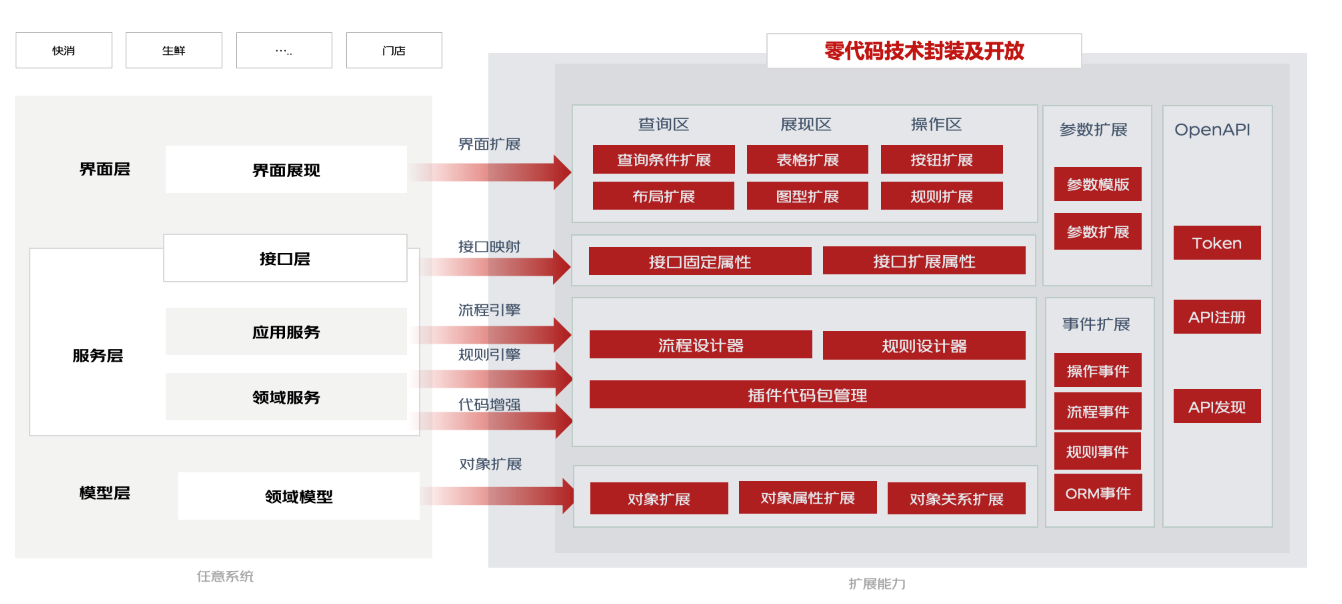
软件架构生态化-多角色交付的探索实践
作为一个技术架构师,不仅仅要紧跟行业技术趋势,还要结合研发团队现状及痛点,探索新的交付方案。在日常中,你是否遇到如下问题 “ 业务需求排期长研发是瓶颈;非研发角色感受不到研发技改提效的变化;引入ISV …...
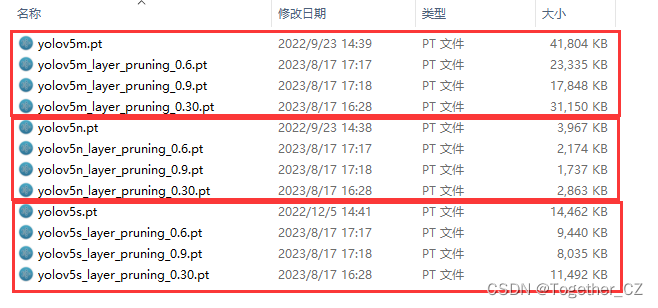
基于YOLOv5n/s/m不同参数量级模型开发构建茶叶嫩芽检测识别模型,使用pruning剪枝技术来对模型进行轻量化处理,探索不同剪枝水平下模型性能影响【续】
这里主要是前一篇博文的后续内容,简单回顾一下:本文选取了n/s/m三款不同量级的模型来依次构建训练模型,所有的参数保持同样的设置,之后探索在不同剪枝处理操作下的性能影响。 在上一篇博文中保持30的剪枝程度得到的效果还是比较理…...
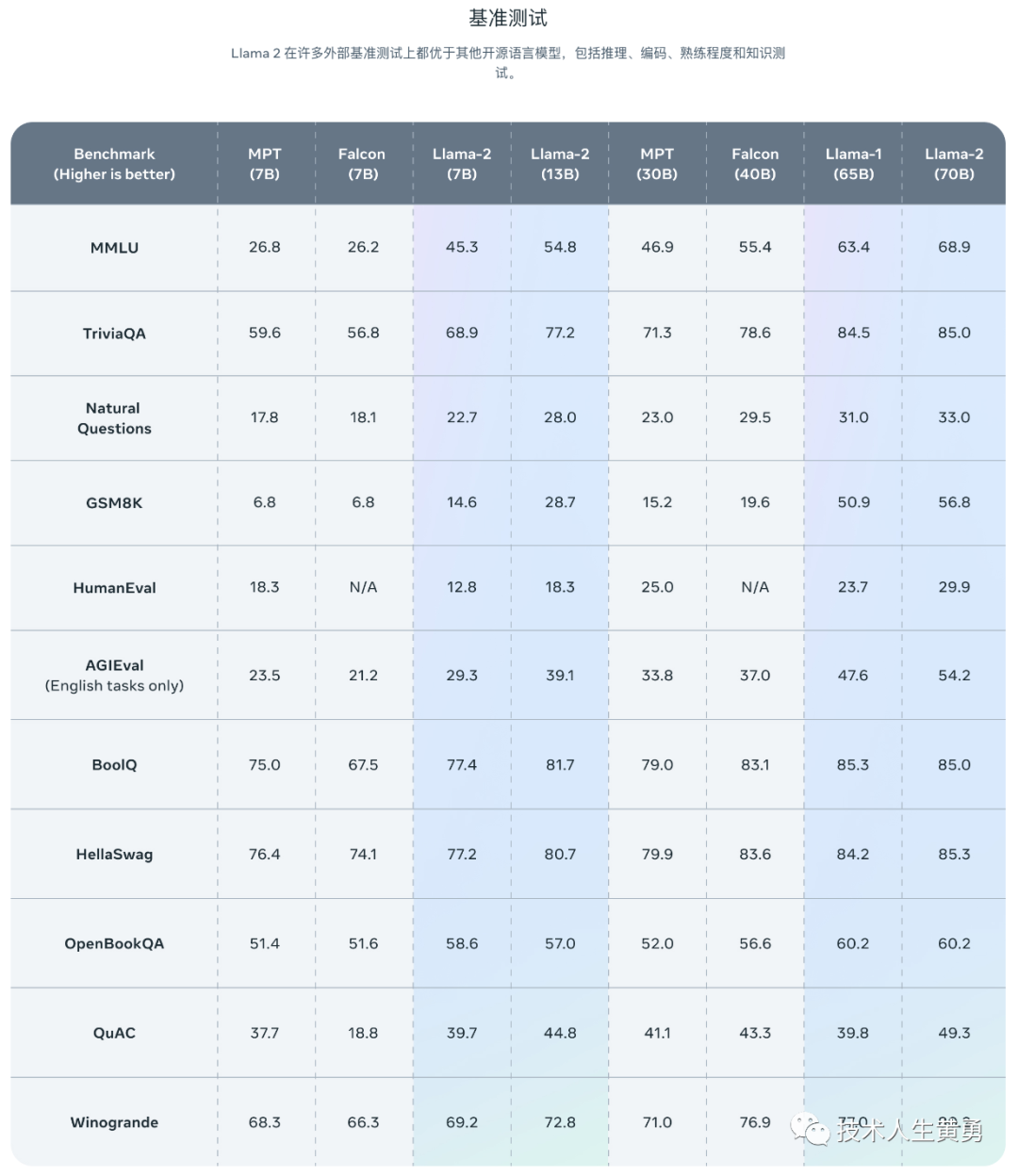
深度解析 Llama 2 的资源汇总:不容错过
“ 探索 Llama 2 背后的过程,包括了模型的全面解析,在线体验,微调,部署等,这份资源汇总将带您深入了解其内涵。” 01 — 周二发布了文章《中文大模型 Chinese-LLaMA-Alpaca-2 开源且可以商用》后,不少朋友们…...
Git 删除 GitHub仓库的文件
新建文件夹 git bash here 在新建的文件夹里右键git bash here打开终端,并执行git init初始化仓库 git clone <你的地址> 找到github上要删除的仓库地址,并复制,在终端里输入git clone <你的地址> 要删除文件的库里右键git b…...

如何使用 ChatGPT 将文本转换为 PowerPoint 演示文稿
推荐:使用 NSDT场景编辑器 助你快速搭建可二次编辑的3D应用场景 步骤 1:将文本转换为幻灯片演示文稿 第一步涉及指示 ChatGPT 根据给定的文本生成具有特定数量幻灯片的演示文稿。首先,您必须向 ChatGPT 提供要转换的文本。 使用以下提示指示…...

html(七)meta标签
一 meta标签 1、背景:发现自带某些请求头2、本文没有实际的生产应用场景,仅仅作为技术积累 ① meta标签含义 1、metadata: 元数据,是用于描述数据的数据,它不会显示在页面上,但是机器却可以识别2、应用场景: [1]、SEO搜索引擎优化[2]、定义页面使用…...
)
《Go 语言第一课》课程学习笔记(五)
入口函数与包初始化:搞清 Go 程序的执行次序 main.main 函数:Go 应用的入口函数 Go 语言中有一个特殊的函数:main 包中的 main 函数,也就是 main.main,它是所有 Go 可执行程序的用户层执行逻辑的入口函数。 Go 程序在…...

Golang 并发编程基础
runtime 包,定义了协程管理相关的 API runtime.Gosched() package mainimport ("fmt""runtime" )func main() {go func() {for i : 0; i < 5; i {fmt.Println(i)}}()// 让出当前CPU给其他协程runtime.Gosched()fmt.Println("end...&qu…...

代码随想录算法训练营(二叉树总结篇)
一.二叉树的种类 1.满二叉树:就是说每一个非叶子节点的节点都有两个子节点。 2.完全二叉树:此二叉树只有最后一层可能没填满,并且存在的叶子节点都集中在左侧!!! (满二叉树也是完全二叉树&…...
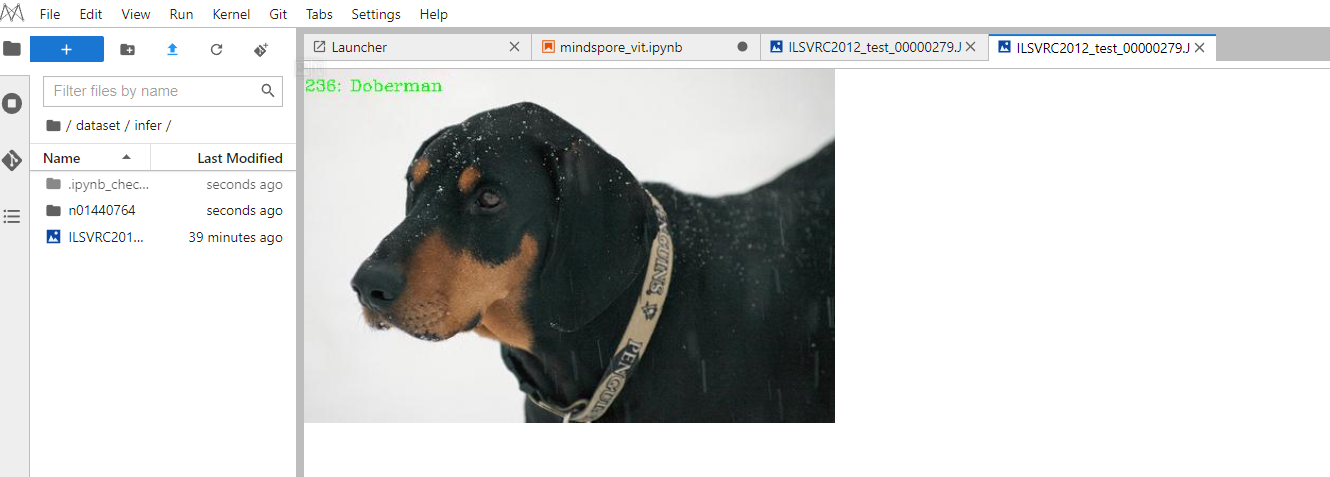
华为开源自研AI框架昇思MindSpore应用案例:基于MindSpore框架的UNet-2D案例实现
目录 一、环境准备1.进入ModelArts官网2.使用CodeLab体验Notebook实例 二、环境准备与数据读取三、模型解析Transformer基本原理Attention模块 Transformer EncoderViT模型的输入整体构建ViT 四、模型训练与推理模型训练模型验证模型推理 近些年,随着基于自注意&…...
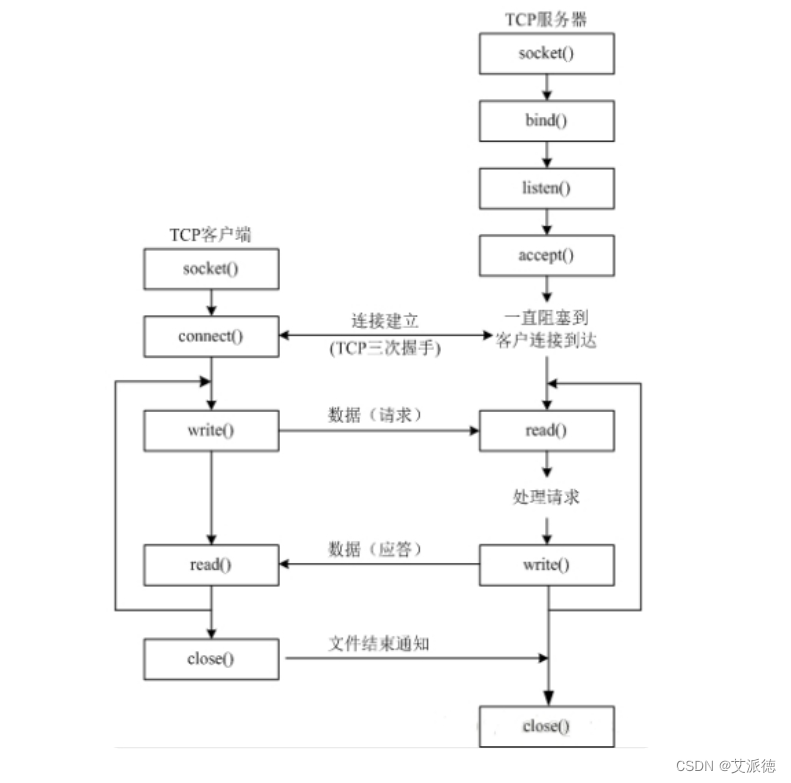
Python入门【TCP建立连接的三次握手、 TCP断开连接的四次挥手、套接字编程实战、 TCP编程的实现、TCP双向持续通信】(二十七)
👏作者简介:大家好,我是爱敲代码的小王,CSDN博客博主,Python小白 📕系列专栏:python入门到实战、Python爬虫开发、Python办公自动化、Python数据分析、Python前后端开发 📧如果文章知识点有错误…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...