当前位置： 首页 > news >正文

Git 删除 GitHub仓库的文件

news 2026/2/11 4:05:48

  1. 新建文件夹

  2. git bash here
    在新建的文件夹里右键git bash here打开终端，并执行git init初始化仓库

  3. git clone <你的地址>
    找到github上要删除的仓库地址，并复制，在终端里输入git clone <你的地址>

  4. 要删除文件的库里右键git bash here打开终端

  5. 在终端里输入dir查看此文件夹下的文件和目录（文件夹）

  6. 删除本地仓库文件夹 git rm -r  删除文件夹的名称，是你要删除的文件夹名字

  7. 删除完你需要删除的文件和文件夹以后，在终端里提交本次修改 git commit -m "备注"
  8. 把删除的文件恢复到最新版本 git checkout
  9. 将本地内容推送到远程仓库 git push


 

相关文章：

Git 删除 GitHub仓库的文件

新建文件夹 git bash here 在新建的文件夹里右键git bash here打开终端&#xff0c;并执行git init初始化仓库 git clone <你的地址> 找到github上要删除的仓库地址&#xff0c;并复制&#xff0c;在终端里输入git clone <你的地址> 要删除文件的库里右键git b…...

编程日记 2023/8/18 12:10:20

如何使用 ChatGPT 将文本转换为 PowerPoint 演示文稿

推荐&#xff1a;使用 NSDT场景编辑器 助你快速搭建可二次编辑的3D应用场景 步骤 1&#xff1a;将文本转换为幻灯片演示文稿 第一步涉及指示 ChatGPT 根据给定的文本生成具有特定数量幻灯片的演示文稿。首先&#xff0c;您必须向 ChatGPT 提供要转换的文本。 使用以下提示指示…...

编程日记 2023/8/18 12:09:14

html(七)meta标签

一 meta标签 1、背景&#xff1a;发现自带某些请求头2、本文没有实际的生产应用场景,仅仅作为技术积累 ① meta标签含义 1、metadata: 元数据,是用于描述数据的数据,它不会显示在页面上,但是机器却可以识别2、应用场景&#xff1a; [1]、SEO搜索引擎优化[2]、定义页面使用…...

编程日记 2023/8/18 12:08:13

《Go 语言第一课》课程学习笔记（五）

入口函数与包初始化&#xff1a;搞清 Go 程序的执行次序 main.main 函数&#xff1a;Go 应用的入口函数 Go 语言中有一个特殊的函数&#xff1a;main 包中的 main 函数&#xff0c;也就是 main.main&#xff0c;它是所有 Go 可执行程序的用户层执行逻辑的入口函数。 Go 程序在…...

编程日记 2023/8/18 12:07:12

Golang 并发编程基础

runtime 包&#xff0c;定义了协程管理相关的 API runtime.Gosched() package mainimport ("fmt""runtime" )func main() {go func() {for i : 0; i < 5; i {fmt.Println(i)}}()// 让出当前CPU给其他协程runtime.Gosched()fmt.Println("end...&qu…...

编程日记 2023/8/18 12:06:10

代码随想录算法训练营（二叉树总结篇）

一.二叉树的种类 1.满二叉树&#xff1a;就是说每一个非叶子节点的节点都有两个子节点。 2.完全二叉树&#xff1a;此二叉树只有最后一层可能没填满&#xff0c;并且存在的叶子节点都集中在左侧&#xff01;&#xff01;&#xff01; &#xff08;满二叉树也是完全二叉树&…...

编程日记 2023/8/18 12:05:09

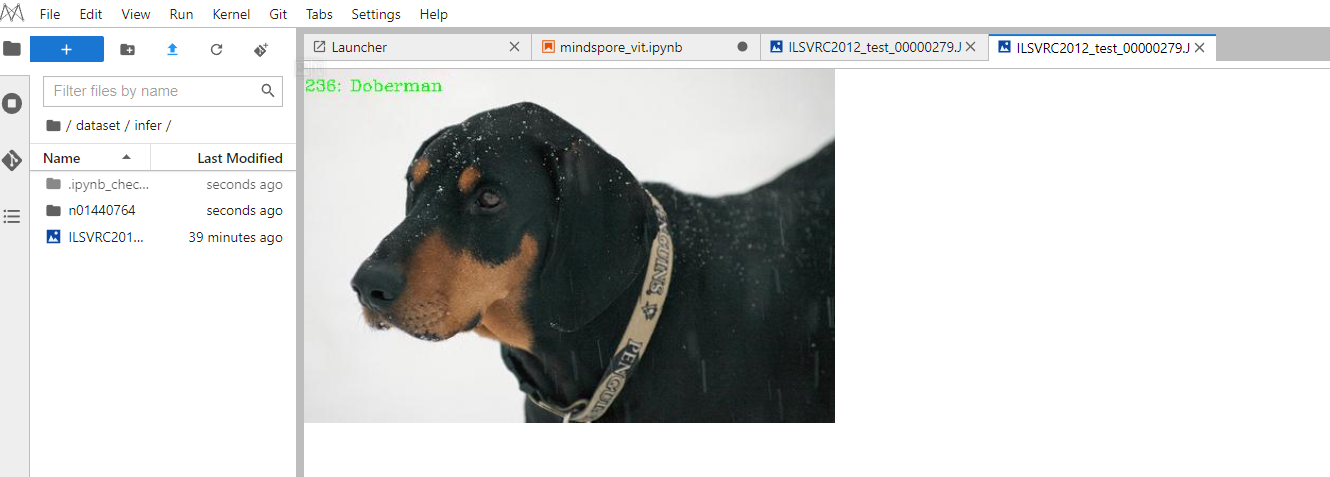
华为开源自研AI框架昇思MindSpore应用案例：基于MindSpore框架的UNet-2D案例实现

目录 一、环境准备1.进入ModelArts官网2.使用CodeLab体验Notebook实例 二、环境准备与数据读取三、模型解析Transformer基本原理Attention模块 Transformer EncoderViT模型的输入整体构建ViT 四、模型训练与推理模型训练模型验证模型推理 近些年&#xff0c;随着基于自注意&…...

编程日记 2023/8/18 12:04:08

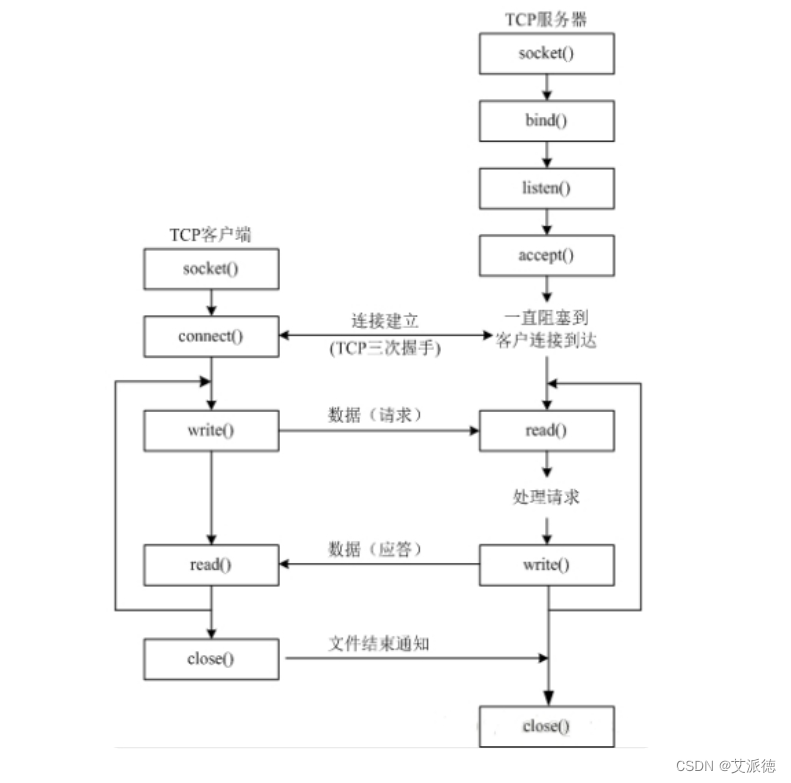
Python入门【TCP建立连接的三次握手、 TCP断开连接的四次挥手、套接字编程实战、 TCP编程的实现、TCP双向持续通信】(二十七)

&#x1f44f;作者简介&#xff1a;大家好&#xff0c;我是爱敲代码的小王&#xff0c;CSDN博客博主,Python小白 &#x1f4d5;系列专栏&#xff1a;python入门到实战、Python爬虫开发、Python办公自动化、Python数据分析、Python前后端开发 &#x1f4e7;如果文章知识点有错误…...

编程日记 2023/8/18 12:03:05

React笔记-React入门

主要是现在要改一个开源项目&#xff0c;需要学习下React入门&#xff0c;在此记录一下。 几个关键的库 React底层核心&#xff1a;react.development.js React操作DOM库&#xff1a;react-dom.development.js 解析ES6语法&#xff1a;babel.min.js React.createElement() …...

编程日记 2023/8/18 12:02:01

SD WebUI 扩展：prompt-all-in-one

sd-webui-prompt-all-in-one 是一个基于 Stable Diffusion WebUI 的扩展&#xff0c;旨在提高提示词/反向提示词输入框的使用体验。它拥有更直观、强大的输入界面功能&#xff0c;它提供了自动翻译、历史记录和收藏等功能&#xff0c;它支持多种语言&#xff0c;满足不同用户的…...

编程日记 2023/8/18 12:01:00

Go和Java实现中介者模式

Go和Java实现中介者模式 下面通过一个同事之间相互通信的例子来说明中介者模式的使用。 1、中介者模式 中介者模式是用来降低多个对象和类之间的通信复杂性。这种模式提供了一个中介类&#xff0c;该类通常处理不同类之间的 通信&#xff0c;并支持松耦合&#xff0c;使代码…...

编程日记 2023/8/18 11:59:59

CentOS系统环境搭建（十五）——CentOS安装Kibana

centos系统环境搭建专栏&#x1f517;点击跳转 关于Elasticsearch的安装请看CentOS系统环境搭建&#xff08;十二&#xff09;——CentOS7安装Elasticsearch。 CentOS安装Kibana 文章目录 CentOS安装Kibana1.下载2.上传3.解压4.修改kibana配置文件5.授予es用户权限6.kibana 后台…...

编程日记 2023/8/18 11:58:57

简单的洗牌算法

目录 前言 问题 代码展现及分析 poker类 game类 Text类 前言 洗牌算法为ArrayList具体使用的典例&#xff0c;可以很好的让我们快速熟系ArrayList的用法。如果你对ArrayList还不太了解除&#xff0c;推荐先看本博主的ArrayList的详解。 ArrayList的详解_WHabcwu的博客-CSD…...

编程日记 2023/8/18 11:57:55

vscode用ssh远程连接linux

1、vscode是利用ssh远程连接linux的&#xff0c;所以首先确保vscode已经安装了这两个插件 2、点击左下角的连接 3、选择Connect to Host…… 5、按格式输入 ssh 主机名ip 比如我的&#xff1a;ssh mnt192.168.198.128 6、选择第一个打开配置文件&#xff0c;确保输入正确 7、…...

编程日记 2023/8/18 11:56:53

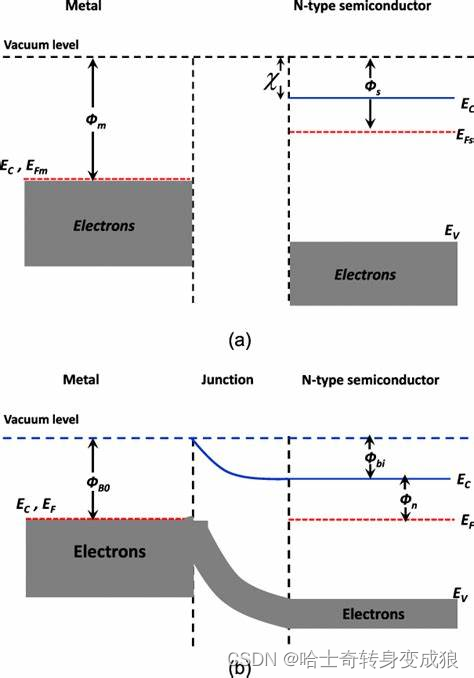
chapter 3 Free electrons in solid - 3.2 量子自由电子理论对一些现象的解释

3.2 自由电子气的热容 Heat capacity of free electron gas 3.2.1 计算自由电子的热容 Calculation of Heat Capacity of free Electrons T>0K, total energy of free electrons: E ∫ E d N 3 5 N e E F 0 [ 1 5 12 π 2 ( k B T E F 0 ) 2 ] E \int EdN \frac{3}{5}…...

编程日记 2023/8/18 11:55:50

vue实现打印功能

在Vue应用中调用打印机功能&#xff0c;可以使用JavaScript的window.print()方法。这个方法会打开打印对话框&#xff0c;然后让我们选择打印设置并打印文档&#xff0c;但是尼这种方法依赖于浏览器的打印功能。 以下是一个简单的示例&#xff0c;演示如何在Vue组件中调用打印…...

编程日记 2023/8/18 11:54:48

golang—面试题大全

目录标题 sliceslice和array的区别slice扩容机制slice是否线程安全slice分配到栈上还是堆上扩容过程中是否重新写入go深拷贝发生在什么情况下&#xff1f;切片的深拷贝是怎么做的copy和左值进行初始化区别slice和map的区别 mapmap介绍map的key的类型map对象如何比较map的底层原…...

编程日记 2023/8/18 11:53:47

Spring、Springboot、SpringCloud--包含的知识点大全

类型难度AOPspring-自定义AOP面向切面注解--统一切面处理-登陆信息采集快速入门SpringbootAOP实现切面处理请求Demo线程池通俗易懂的线程池底层原理&#xff0c;一文知所有数据结构数据结构-链表篇数据结构--数组篇数据结构之-concurrentHashMap源码分析JVMJVM调优及各种问题处…...

编程日记 2023/8/18 11:52:45

MongoDB:数据库初步应用

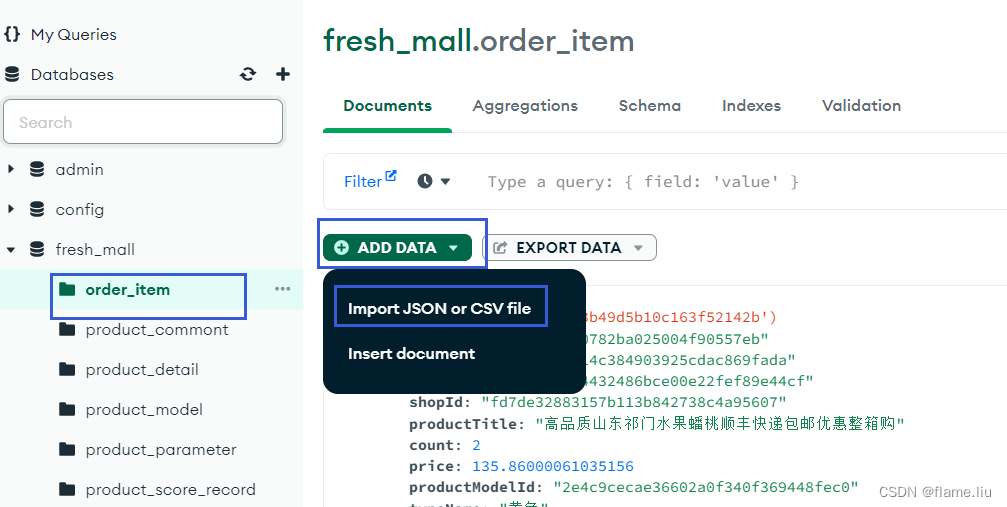
一.连接MongoDB 1.MongoDBCompass连接数据库 连接路径:mongodb://用户名:密码localhost:27017/ 2.创建数据库(集合) MongoDB中数据库被称为集合. MongoDBCompass连接后,点击红色框加号创建集合,点击蓝色框加号创建文档(数据表) 文档中的数据结构(相当于表中的列)设计不用管…...

编程日记 2023/8/18 11:51:40

C#之枚举中的按位与（）按位或（|）。

一些基础定义&#xff1a; 按位或运算符&#xff08;|&#xff09;是一种位运算符&#xff0c;用来对两个二进制数进行操作。对于每个位上的1&#xff0c;如果至少有一个二进制数中的对应位为1&#xff0c;则结果为1&#xff1b;否则&#xff0c;结果为0。按位与运算符&#x…...

编程日记 2023/8/18 11:50:36

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的？

&#x1f9e0; 智能合约中的数据是如何在区块链中保持一致的&#xff1f; 为什么所有区块链节点都能得出相同结果&#xff1f;合约调用这么复杂&#xff0c;状态真能保持一致吗&#xff1f;本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里&#xf…...

编程新知 2025/10/25 17:23:41

未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？

编辑&#xff1a;陈萍萍的公主一点人工一点智能 未来机器人的大脑&#xff1a;如何用神经网络模拟器实现更智能的决策&#xff1f;RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战&#xff0c;在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

编程新知 2026/2/10 23:40:41

微信小程序之bind和catch

这两个呢&#xff0c;都是绑定事件用的&#xff0c;具体使用有些小区别。 官方文档&#xff1a; 事件冒泡处理不同 bind&#xff1a;绑定的事件会向上冒泡&#xff0c;即触发当前组件的事件后&#xff0c;还会继续触发父组件的相同事件。例如&#xff0c;有一个子视图绑定了b…...

编程新知 2026/2/5 5:05:56

23-Oracle 23 ai 区块链表（Blockchain Table）

小伙伴有没有在金融强合规的领域中遇见&#xff0c;必须要保持数据不可变&#xff0c;管理员都无法修改和留痕的要求。比如医疗的电子病历中&#xff0c;影像检查检验结果不可篡改行的&#xff0c;药品追溯过程中数据只可插入无法删除的特性需求&#xff1b;登录日志、修改日志…...

编程新知 2026/2/10 8:01:46

STM32标准库-DMA直接存储器存取

文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA&#xff08;Direct Memory Access&#xff09;直接存储器存取 DMA可以提供外设…...

编程新知 2026/1/26 10:55:51

【单片机期末】单片机系统设计

主要内容&#xff1a;系统状态机&#xff0c;系统时基&#xff0c;系统需求分析&#xff0c;系统构建&#xff0c;系统状态流图 一、题目要求 二、绘制系统状态流图 题目&#xff1a;根据上述描述绘制系统状态流图&#xff0c;注明状态转移条件及方向。 三、利用定时器产生时…...

编程新知 2026/1/31 12:27:36

AI，如何重构理解、匹配与决策？

AI 时代&#xff0c;我们如何理解消费&#xff1f; 作者&#xff5c;王彬 封面&#xff5c;Unplash 人们通过信息理解世界。 曾几何时&#xff0c;PC 与移动互联网重塑了人们的购物路径&#xff1a;信息变得唾手可得&#xff0c;商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2026/1/30 2:33:11

算法：模拟

1.替换所有的问号 1576. 替换所有的问号 - 力扣&#xff08;LeetCode&#xff09; ​遍历字符串​&#xff1a;通过外层循环逐一检查每个字符。​遇到 ? 时处理​&#xff1a; 内层循环遍历小写字母&#xff08;a 到 z&#xff09;。对每个字母检查是否满足&#xff1a; ​与…...

编程新知 2026/2/10 11:15:52

推荐 github 项目:GeminiImageApp(图片生成方向，可以做一定的素材)

推荐 github 项目:GeminiImageApp(图片生成方向&#xff0c;可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

编程新知 2026/1/25 10:41:07

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00