【LeetCode】88.合并两个有序数组
题目
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
解答
源代码
class Solution {public void merge(int[] nums1, int m, int[] nums2, int n) {int index = m + n - 1;while (n != 0) {if (m == 0) {System.arraycopy(nums2, 0, nums1, 0, index + 1);break;}if (nums1[m - 1] > nums2[n - 1]) {nums1[index] = nums1[m - 1];nums1[m - 1] = 0;m--;} else {nums1[index] = nums2[n - 1];n--;}index--;}}
}总结
从前往后合并对于数组来说很麻烦,那就另辟蹊径,从后往前合并,当nums2中元素全部放入nums1中时合并结束。
相关文章:

【LeetCode】88.合并两个有序数组
题目 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终,合并…...

05 - 研究 .git 目录
查看所有文章链接:(更新中)GIT常用场景- 目录 文章目录 1. HEAD2. config3. refs4. objects 1. HEAD 2. config 3. refs 4. objects Git对象一共有三种:数据对象 blob、树对象 tree以及提交对象 commit,这些对象都被保…...

MySQL之索引和事务
索引什么是索引索引怎么用索引的原理 事务使用事务事务特性MySQL隔离级别 索引 什么是索引 索引包含数据表所有记录的引用指针;你可以对某一列或者多列创建索引和指定不同的类型(唯一索引、主键索引、普通索引等不同类型;他们底层实现也是不…...

⛳ 将本地已有的项目上传到 git 仓库
目录 ⛳ 将本地已有的项目上传到 git 仓库🏭 一、克隆 拷贝🎨 二、强行合并两个仓库 ⛳ 将本地已有的项目上传到 git 仓库 有两种方法: 一、克隆 拷贝 二、强行合并两个仓库 🏭 一、克隆 拷贝 直接用把远程仓库拉到本…...
)
ADB常用命令整理(全网最全)
调试Android程序时,我们经常需要使用adb shell命令。adb是Android Debug Bridge的缩写,它充当调试桥梁的作用,就像一条连接开发机和设备之间的桥梁。 通过adb,我们可以在Eclipse中使用DDMS来调试Android程序,简单来说…...
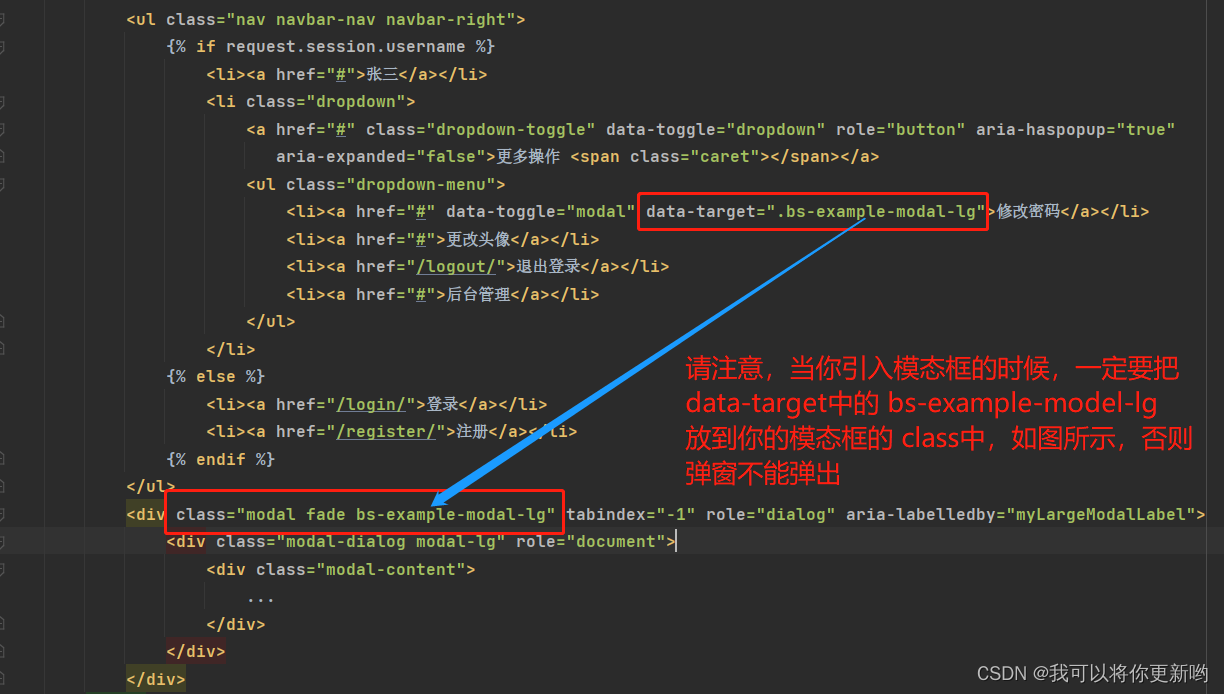
BBS项目day02、注册、登录(登录之随机验证码)、退出登录、密码加密加盐、首页(导航条、模态框,修改密码)
一、注册 1.注册之前端页面 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>注册页面</title><!--动态引入文件-->{% load static %}<script src"{% static js/jquery.min.js %…...
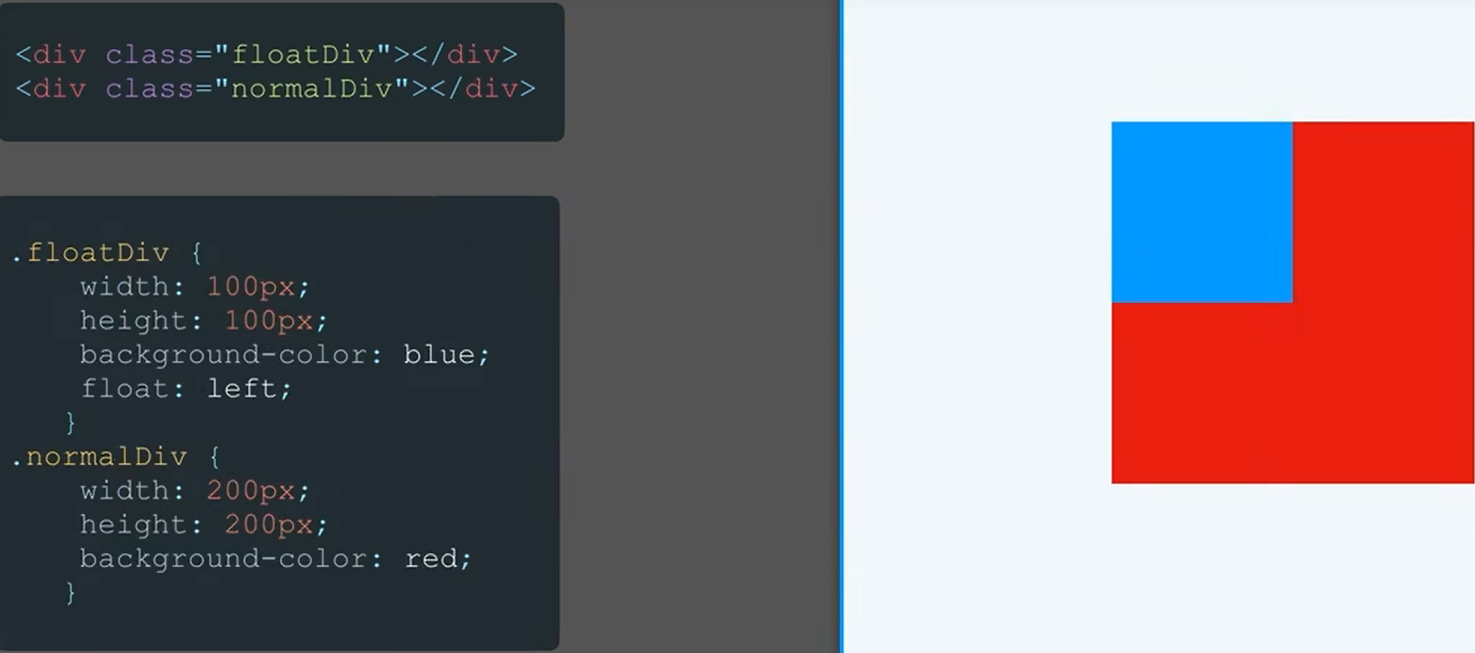
HTML5+CSS3自用笔记
助解:解析编译,加载运行 浏览器的渲染过程 JS加载执行 普通js/sync:阻塞 DOM加载解析 async:下载完就执行,无依赖 <script type"text/javascript" src"x.min.js" async"async"&g…...
)
无则插入有则更新(PostgreSQL,MySQL,Oracle、SqlServer)
无则插入有则更新 PostgreSQL 无则插入有则更新 conflict(带有唯一性约束的字段),根据此字段判断是更新还是插入 INSERT INTO student(id,name,sex) VALUES(1, 小明, 男) ON conflict (id) DO UPDATE SET id 1,name 小明,sex 男;无则插入有则不做操作 INSERT I…...

常见的 JavaScript 框架比较
以下是10种常见的JavaScript框架的比较: React:是由Facebook开发和维护的开源JavaScript库,用于构建用户界面。它允许你使用组件来构建复杂的UI,并专注于每个组件的内部逻辑,而不必担心管理整个应用程序的状态。WebBu…...

基于R语言APSIM模型进阶应用与参数优化、批量模拟
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物生…...

AMD卡启动Stable Diffusion AI绘画的方法
WindowsAMD安装法 1.安装python 3.10.6,在python官网上下载安装程序,***重要*** 在安装的第一个窗口下方勾选“将python添加到path”。 2.安装git 3.WindowsAMD使用AUTOMATIC1111的directml这一个fork,在这个页面的第一段:https:/…...
)
Ubuntu系统kubeadm安装K8S_v1.25.x容器使用docker(K8S_v1.24版本以后依然使用docker容器管理)
安装所需要的全部文档请点击这里下载 系统是: root@k8s-master:~# cat /etc/lsb-release DISTRIB_ID=Ubuntu DISTRIB_RELEASE=22.04 DISTRIB_CODENAME=jammy DISTRIB_DESCRIPTION=“Ubuntu 22.04.3 LTS” root@k8s-master:~# uname -a Linux k8s-master 5.15.0-76-generic #8…...
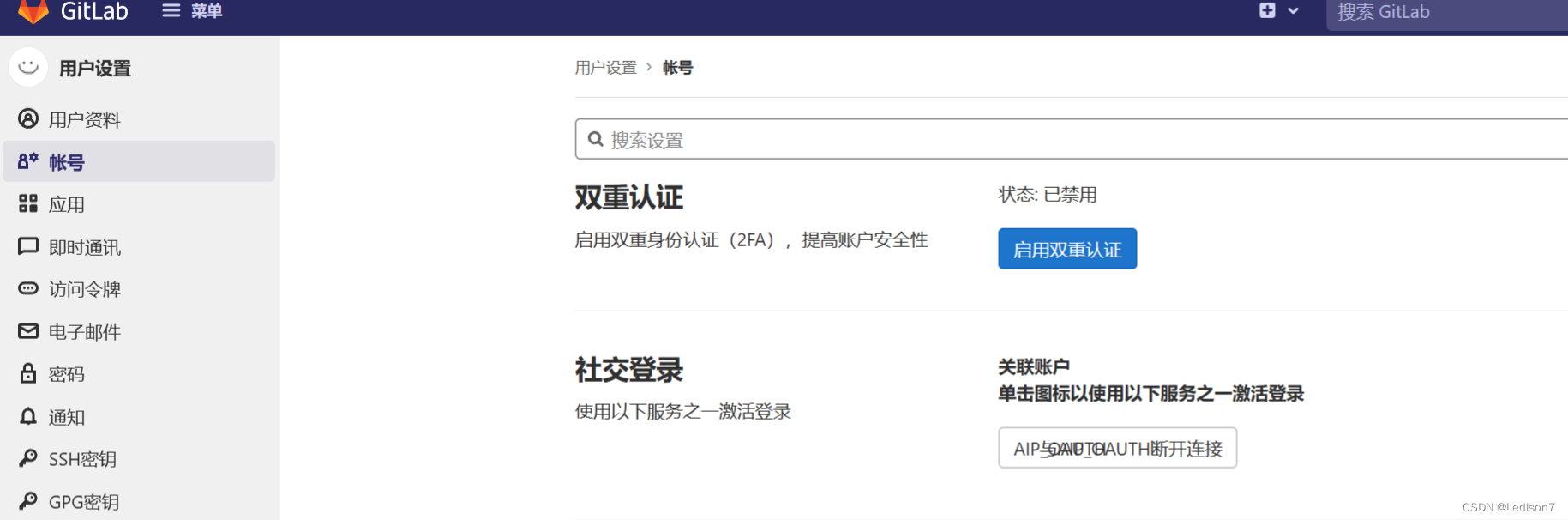
【MaxKey对接一】对接gitlab的oauth登录
MaxKey的Oauth过程 引导进入 GET http://{{maxKey_host}}/sign/authz/oauth/v20/authorize?client_idYOUR_CLIENT_ID&response_typecode&redirect_uriYOUR_REGISTERED_REDIRECT_URI 登录后回调地址 YOUR_REGISTERED_REDIRECT_URI/?code{{code}} 换取Access Token GET…...

【Buildroot】构建根文件系统等
文章目录 0. 前言10. 环境软件硬件 20. Buildroot 环境搭建简述下载环境搭建toolchain下载、安装构建镜像(仅供参考) 80. 问题点1. 编译、清除时提示权限不足 0. 前言 对嵌入式linux开发和linux开发环境不熟悉的同志们就不要往下看了 对嵌入式linux开发和…...
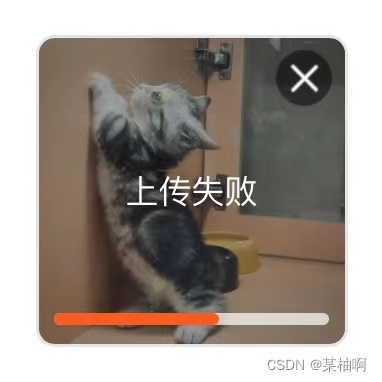
利用css动画和定时器setTimeout,实现上传图片进度条
思路 利用css动画和js定时器(setTimeout),实现简单的进度条。 优势 不使用 setInterval,减少js代码量,业务代码更加简洁。 示意图 上传中上传成功上传失败 代码 html <!-- img-wrap有两种状态:u…...
关于VScode插件,你不得不知道的几件事
一、前言 VSCode是微软家一个非常轻量化的编辑器,体量虽轻,但是却有异常强大的功能。原因在于VSCode许多强大功能都是基于插件实现的,IDE只提供一个最基本的框架和基本功能,我们需要使用插件来丰富和扩展它的功能。 由于插件的重…...

MySQL 奇遇记三则
公司新项目,要使用 MySQL 数据库。 第一次使用 MySQL,有点小激动。听说过 N 多次,这一次终于用上了。 为什么是奇遇记? 因为在网上几乎搜索不到别人遇到和我一样的问题。 系统 :WINDOWS10X64 中文版 数据库…...

UI设计师的主要职责说明(合集)
UI设计师的主要职责说明1 职责: 1、负责公司移动端、PC端产品相关的交互、UI等设计 2、负责公司宣传册、海报、运营物料、banner等设计 3、负责公司品牌相关的视觉设计 3、制定相关设计规范,提高产品的可用性、不断优化产品体验; 4、与PM、运营紧密…...
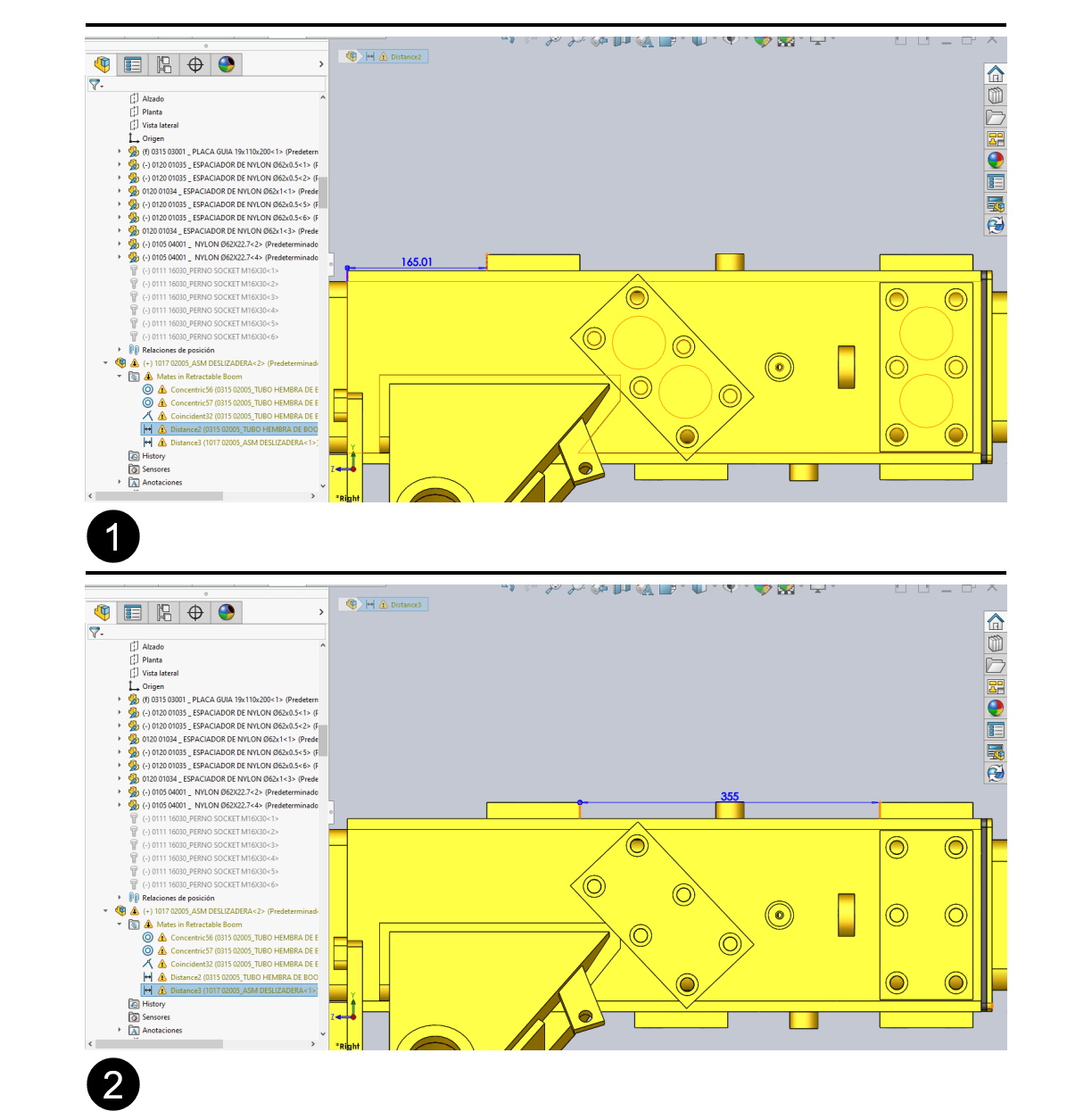
SOLIDWORKS 2023中装配体配合的正确使用方法 硕迪科技
-SOLIDWORKS 装配体打开时是由不同的阶段和性能检查组成的。如果在创建装配体时未应用基本的配合方法,问题会随着时间的推移而累积,并且在使用时会出现明显的速度减慢。 如果您的装配体运行速度很慢,则很可能是在创建配合时出现了不良操作的症…...

代码随想录——96.不同的二叉搜索树
class Solution {public int numTrees(int n) {int[] dp new int[n1];dp[0] 1;dp[1] 1;for(int i 2;i < n ; i){for(int j 1; j < i;j){dp[i] dp[j-1]*dp[i-j];}}return dp[n];} }...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
