回到未来:使用马尔可夫转移矩阵分析时间序列数据

一、说明
在本文中,我们将研究使用马尔可夫转移矩阵重构时间序列数据如何产生有趣的描述性见解以及用于预测、回溯和收敛分析的优雅方法。在时间上来回走动——就像科幻经典《回到未来》中 Doc 改装的 DeLorean 时间机器一样。
注意:以下各节中的所有方程和图表图像均由本文作者创建。
二、基本构建基块
让 E 定义构成时间序列数据的 k 个唯一事件的集合。例如,时间序列可能由以下三个基本且独特的事件组成,这些事件表示在跨离散时间步长绘制数据时观察到的路径轨迹类型:向下、横盘和向上。让 S 定义一个长度为 n 的序列(表示离散时间步长),由 E 中定义的事件组成,表示部分或全部数据。例如,序列 [向上、向下、向上、横盘、向上] 表示数据的五个时间步长。
现在可以定义一个维度为 k² 的马尔可夫转移矩阵 M,使得每个元素 M(i, j) 描述在给定时间序列中从时间步长 t 中的事件 E(i) 过渡到时间步长 t+1 中的事件 E(j) 的概率。换句话说,M(i, j) 表示在连续时间步长内在两个事件之间转换的条件概率。在图论意义上,事件 E(i) 和 E(j) 可以被认为是由有向边 E(i) → E(j) 连接的节点,如果时间序列数据中的 E(i) 后跟 E(j); 则马尔可夫转移矩阵 M 本质上表示图中节点所描述的事件的邻接矩阵(或共生矩阵)的规范化版本。
接下来,让我们看看我们可以用这些基本构建块做什么。
三、过渡矩阵的实际应用:一个简单的例子
假设我们有以下涵盖 11 个连续时间步长的原始时间序列数据:[1, 2, -2, -1, 0, 0, 2, 2, 1, 2, 3]。 使用上述路径轨迹的简化视图,我们可以将数据转换为以下 10 个事件的序列,这些事件描述了相邻时间步之间的转换:[向上、向下、向上、向上、向上、向上、向上、向上、 平坦,向上,持平,向下,向上,向上]。
现在,我们可以构造以下邻接矩阵,用于捕获事件序列中的重合模式:
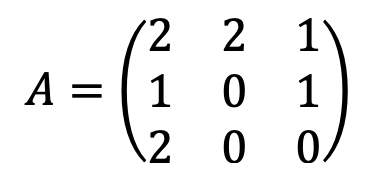
元素 A(i, j) 表示在我们的事件序列中,事件 i 在某个时间步 t 处后跟事件 j 在时间步长 t+1 的次数;i 和 j 分别是行索引和列索引。请注意,行按从上到下的顺序表示事件,列表示从左到右的顺序相同。例如,A 的左上角元素表示在给定事件序列中,一个 up 事件后跟另一个 up 事件两次。A 的右中元素表示,在事件序列中,一个横盘事件后跟一个下降事件。等等。
我们可以按行或按列规范化矩阵 A 以生成过渡矩阵。如果我们要使用基于行的规范化,那么元素 M(i, j) 将描述在时间步长 t+1 中看到事件 E(j) 的概率,给定时间步长 t 中的事件 E(i)。因此,每行中的概率总和应为 1。在我们的示例中,行规范化矩阵如下所示:

同样,如果我们要使用基于列的归一化,那么元素 M(i, j) 将描述在给定时间步长 t 中的事件 E(j) 的情况下,在时间步长 t-1 中具有事件 E(i) 的概率。现在,每列中的概率总和应为 1。在我们的示例中,列规范化矩阵如下所示:

请注意,行规范化的条件概率(名义上是向前移动)可能与列规范化的条件概率(向后看时间)不同。
四、Python 代码中的示例
为了尝试这些概念,这里有一些基本的 Python 代码,用于捕获上面示例中发生的情况。
确保先安装了 Pandas 软件包:
pip install pandas==0.25.2然后运行以下代码:
import pandas as pd# Define helper functions
def get_transition_tuples(ls):''' Converts a time series into a list of transition tuples'''return [(ls[i-1], ls[i]) for i in range(1, len(ls))]def get_transition_event(tup):''' Converts a tuple into a discrete transition event'''transition_event = 'flat'if tup[0] < tup[1]:transition_event = 'up'if tup[0] > tup[1]:transition_event = 'down'return transition_event# Generate raw time series data
ls_raw_time_series = [1, 2, -2, -1, 0, 0, 2, 2, 1, 2, 3]# Derive single-step state transition tuples
ls_transitions = get_transition_tuples(ls_raw_time_series)# Convert raw time series data into discrete events
ls_events = [get_transition_event(tup) for tup in ls_transitions]
ls_event_transitions = get_transition_tuples(ls_events)# Create an index (list) of unique event types
ls_index = ['up', 'flat', 'down']# Initialize Markov transition matrix with zeros
df = pd.DataFrame(0, index=ls_index, columns=ls_index)# Derive transition matrix (or co-occurrence matrix)
for i, j in ls_event_transitions:df[j][i] += 1 # Update j-th column and i-th row''' Derive row-normalized transition matrix:
- Elements are normalized by row sum (fill NAs/NaNs with 0s)
- df.sum(axis=1) sums up each row, df.div(..., axis=0) then divides each column element
'''
df_rnorm = df.div(df.sum(axis=1), axis=0).fillna(0.00)''' Derive column-normalized transition matrix:
- Elements are normalized by column sum (fill NAs/NaNs with 0s)
- df.sum(axis=0) sums up each col, df.div(..., axis=1) then divides each row element
'''
df_cnorm = df.div(df.sum(axis=0), axis=1).fillna(0.00)这应该产生以下转移矩阵:
>>> df # Transition matrix with raw event co-occurrencesup flat down
up 2 2 1
flat 1 0 1
down 2 0 0
>>> df_rnorm # Row-normalized transition matrixup flat down
up 0.4 0.4 0.2
flat 0.5 0.0 0.5
down 1.0 0.0 0.0
>>> df_cnorm # Column-normalized transition matrixup flat down
up 0.4 1.0 0.5
flat 0.2 0.0 0.5
down 0.4 0.0 0.0可视化转移矩阵的一种巧妙方法是使用Graphviz或NetworkX等图形包将它们描述为有向加权图。
我们将在这里使用 Graphviz,因此您需要安装软件包才能跟进:
pip install graphviz==0.13.2值得浏览简短而甜蜜的官方安装指南,以确保您正确设置了软件包,特别是对于可能需要执行一些其他安装步骤的 Windows 用户。
设置 Graphviz 后,创建一些用于绘图的辅助函数:
from graphviz import Digraph# Define functions to visualize transition matrices as graphsdef get_df_edgelist(df, ls_index):''' Derive an edge list with weight values'''edgelist = []for i in ls_index:for j in ls_index:edgelist.append([i, j, df[j][i]])return pd.DataFrame(edgelist, columns=['src', 'dst', 'weight'])def edgelist_to_digraph(df_edgelist):''' Convert an edge list into a weighted directed graph'''g = Digraph(format='jpeg')g.attr(rankdir='LR', size='30')g.attr('node', shape='circle')nodelist = []for _, row in df_edgelist.iterrows():node1, node2, weight = [str(item) for item in row]if node1 not in nodelist:g.node(node1, **{'width': '1', 'height': '1'})nodelist.append(node1)if node2 not in nodelist:g.node(node2, **{'width': '1', 'height': '1'})nodelist.append(node2)g.edge(node1, node2, label=weight)return gdef render_graph(fname, df, ls_index):''' Render a visual graph and saves it to disk'''df_edgelist = get_df_edgelist(df, ls_index)g = edgelist_to_digraph(df_edgelist)g.render(fname, view=True)现在,您可以生成每个转移矩阵。默认情况下,输出的图形将存储在您的工作目录中。
# Generate graph of transition matrix (raw co-occurrences)
render_graph('adjmat', df, ls_index)# Generate graph of row-normalized transition matrix
render_graph('transmat_rnorm', df_rnorm, ls_index)# Generate graph of column-normalized transition matrix
render_graph('transmat_cnorm', df_cnorm, ls_index)原始共现:

行归一化转移概率:
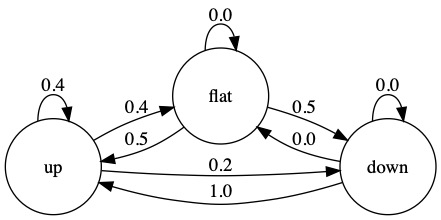
列归一化转移概率:

五、实际应用
5.1描述性见解
我们可以对过渡矩阵做的第一件事也是最明显的事情是仅通过检查矩阵及其可视化图形表示来获得描述性见解。例如,通过上一节中示例的输出,我们可以收集如下高级见解:
- 在 9 个可能的事件转换中,有 3 个从未在我们的样本中发生(平坦→平坦、向下→向下和向下→平坦)。连续横盘事件的低概率可能表示时间序列数据正在跟踪的系统存在波动性。
- up 事件是唯一具有连续发生非零概率 (0.4) 的事件类型。事实上,这种转变概率是我们数据中最高的概率之一,可能表明数据基础系统中的强化效应。
- 在我们的例子中,基于行和基于列的归一化会产生不同的矩阵,尽管有一些重叠。这告诉我们,我们的时间序列在时间上本质上是不对称的,也就是说,我们看到的模式有些不同,这取决于我们是从给定的参考点回顾还是向前看。
5.2 预测和回溯
通过将过渡矩阵的副本链接在一起,我们可以生成事件在时间上向前和向后发生的概率;这可以分别称为预测和反向预测。这里的一个中心假设是“历史无关紧要”;无论我们以什么时间步长 T 作为参考点,我们假设转移矩阵给出了 T+1(如果行归一化)和 T-1(如果列归一化)的相关概率。结果是,我们可以使用过渡矩阵从任意时间步进行预测和回溯。特别是,我们可以使用行规范化过渡矩阵进行预测,使用列规范化过渡矩阵进行反向预报。
采用上面示例中计算的矩阵,假设我们在时间步长 t = 25 处观察到一个向上事件,并且我们希望预测哪个事件最有可能在时间步长 t = 27 发生。通过检查行归一化转移矩阵的第一行,我们直接看到,在下一个时间步长t = 26,观察到向上,横盘和向下事件的概率分别为0.4,0.4和0.2。为了推导出时间步长 t = 27 的类似事件概率(即,从我们的参考点开始的两个时间步长),我们需要将转移矩阵本身相乘,如下所示:

请注意事件概率相对于我们的参考时间步长是如何变化的。例如,给定一个向上事件在t = 25时,观察到另一个上升事件的概率在t = 0时为4.26(向未来一步),在t = 0(向未来两步)时增加到56.27。 同时,在t = 0时观察到横盘事件的概率也是4.26,但在t = 0时降低到16.27。至关重要的是,这种矩阵乘法方法支持预测和回播。通常,为了预测或反向预测 n 次方之外的事件概率,我们可以分别计算行归一化或列归一化过渡矩阵到 n 次方。
转移矩阵还可用于预测原始基础时间序列数据。让我们假设一个上升或下降事件相当于时间序列数据中的单个变化单位。现在假设时间序列在 t = 1 时从 2 上升到 25(向上事件),我们希望预测时间序列在 t = 26 和 t = 27 处的进展。 在上升事件之后,上升和横盘事件在t = 0时发生的可能性最高(4.26)。因此,我们可以预测,在 t = 26 时,时间序列很可能是 [1, 2, 3] 或 [1, 2, 2],这两者都可能在 t = 27 时分别产生两种可能性:[1, 2, 3] 导致 [1, 2, 3, 4] 或 [1, 2, 3, 3](概率各为 0.4,和以前一样), 和 [1, 2, 2] 导致 [1, 2, 2, 3] 或 [1, 2, 2, 1](每个概率为 0.5)。通常,我们期望用于生成转移矩阵的数据集越大、越丰富,在潜在事件链方面捕获的方差就越大,因此逐步预测精度就越高。
转移矩阵的乘法链导致原始事件转移概率的日益复杂但完全可分解的组合。这种可分解性可以帮助我们更深入地了解构成时间序列数据(或随机过程)的事件的相互依赖性。
5.3 收敛分析
将转移矩阵链接在一起的概念自然会引出一个有趣的问题:转移矩阵 M 的概率会收敛吗?具体来说,是否存在稳定的过渡矩阵 M*,使得 MM*=M*?如果是这样,那么 lim(n → ∞)Mⁿ = M*,即,我们期望由矩阵乘法链 Mⁿ 表示的马尔可夫过程在某个时间点收敛到稳定状态 M*;在这种情况下,该过程是收敛的,因此是稳定的。假设我们的转移矩阵是行规范化的,元素 M*(i, j) 为我们提供了事件 i 后跟事件 j 的稳定长期概率。但是,如果找不到稳定的矩阵 M*,则该过程是非收敛和不稳定的。
使用前面几节中的运行示例,我们可以简要地勾勒出如何解析马尔可夫过程的收敛性。
首先,我们假设有一个稳定的转移矩阵 M*,使得 MM*=M*,并且 M 是行归一化的。既然我们知道 M 是什么样子的,我们可以写出矩阵乘法如下:

然后我们有以下线性方程组:
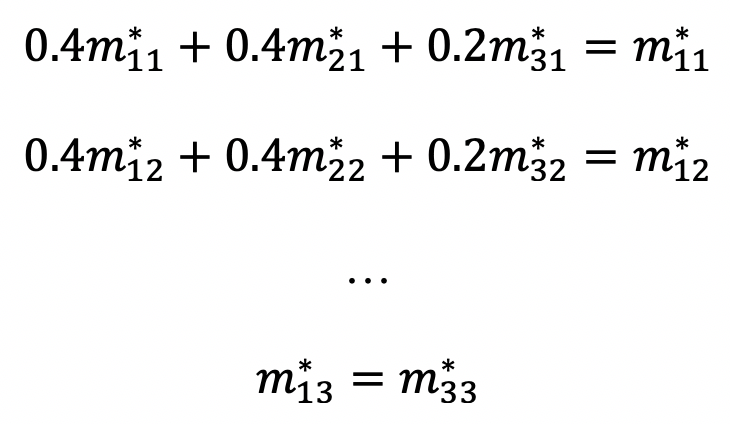
如果这个方程组存在一个解(我们可以使用高斯消除等方法进行检查),那么我们也可以推导出一个收敛且稳定的转移矩阵。
六、包装
一旦掌握了窍门,使用马尔可夫转移矩阵重构时间序列数据可以成为数据科学工具包的有用部分。正如您通常使用折线图可视化时间序列数据以更好地了解整体趋势一样,过渡矩阵提供了高度压缩但在其用例中通用的数据的补充表示形式。当可视化为有向图时,转移矩阵已经可用于获得高级描述性见解。当嵌入到更大的工作流中时,过渡矩阵可以构成更复杂的预测和回溯方法的基础。此外,虽然我们在上述部分中运行的简单示例将转移矩阵视为静态实体,但我们可以为不同的时间间隔推导出不同的矩阵;这在分析时间序列数据时特别有用,这些数据显示由数据中显著的 U 形或肘形模式反映的明显趋势反转。显然,上面讨论的想法有几个可能的扩展,所以继续尝试它们 - 它们可能会在你的下一个数据科学项目中派上用场。
参考资料:Time Series Data and Markov Transition Matrices | Towards Data Science
相关文章:
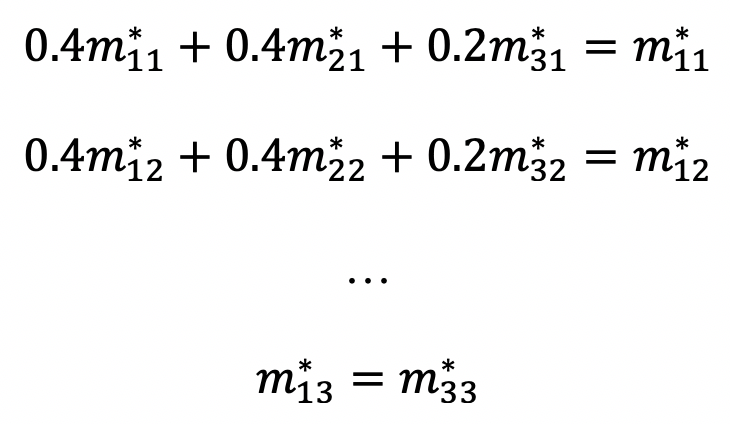
回到未来:使用马尔可夫转移矩阵分析时间序列数据
一、说明 在本文中,我们将研究使用马尔可夫转移矩阵重构时间序列数据如何产生有趣的描述性见解以及用于预测、回溯和收敛分析的优雅方法。在时间上来回走动——就像科幻经典《回到未来》中 Doc 改装的 DeLorean 时间机器一样。 注意:以下各节中的所有方程…...

vue element 多图片组合预览
定义组件:preview-image <template><div><div class"imgbox"><divclass"preview-img":class"boxClass"v-if"Imageslist 3 ||Imageslist 5 ||Imageslist 7 ||Imageslist 8 ||Imageslist > 9"&…...
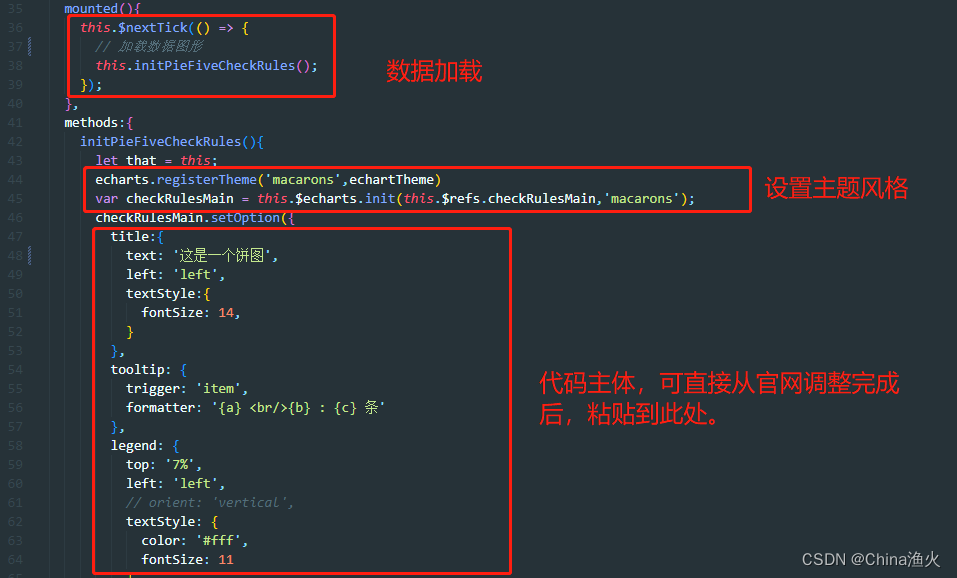
Vue2集成Echarts实现可视化图表
一、依赖配置 1、引入echarts相关依赖 也可以卸载原有的,重新安装 卸载:npm uninstall echarts --save 安装:npm install echarts4.8.0 --save 引入水球图形依赖 npm install echarts-liquidfill2.0.2 --save 水球图可参考文档࿱…...
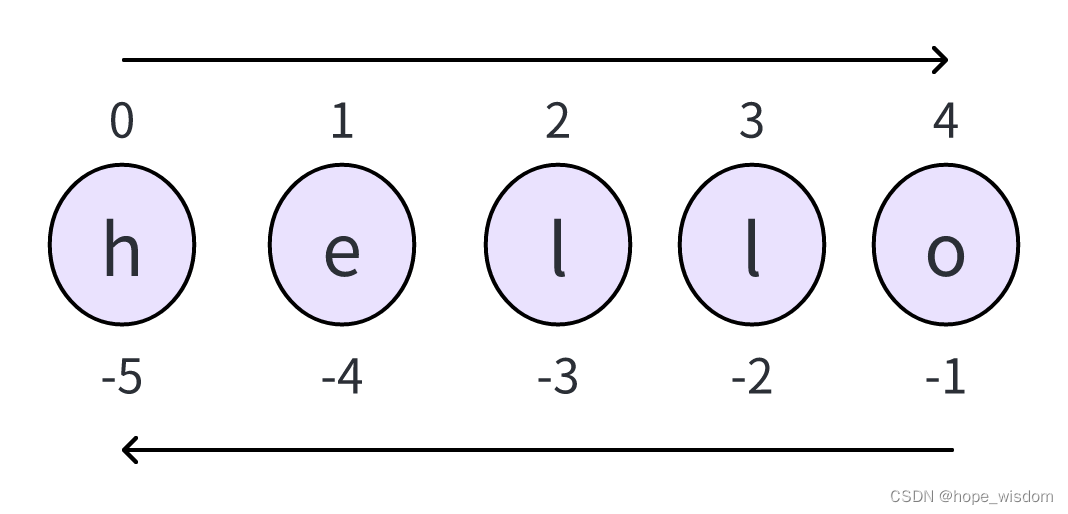
3 Python的数据类型
概述 在上一节,我们介绍了Python的基础语法,包括:编码格式、标识符、关键字、注释、多行、空行、缩进、引号、输入输出、import、运算符、条件控制、循环等内容。Python是一种动态类型的编程语言,这意味着当你创建一个变量时&…...
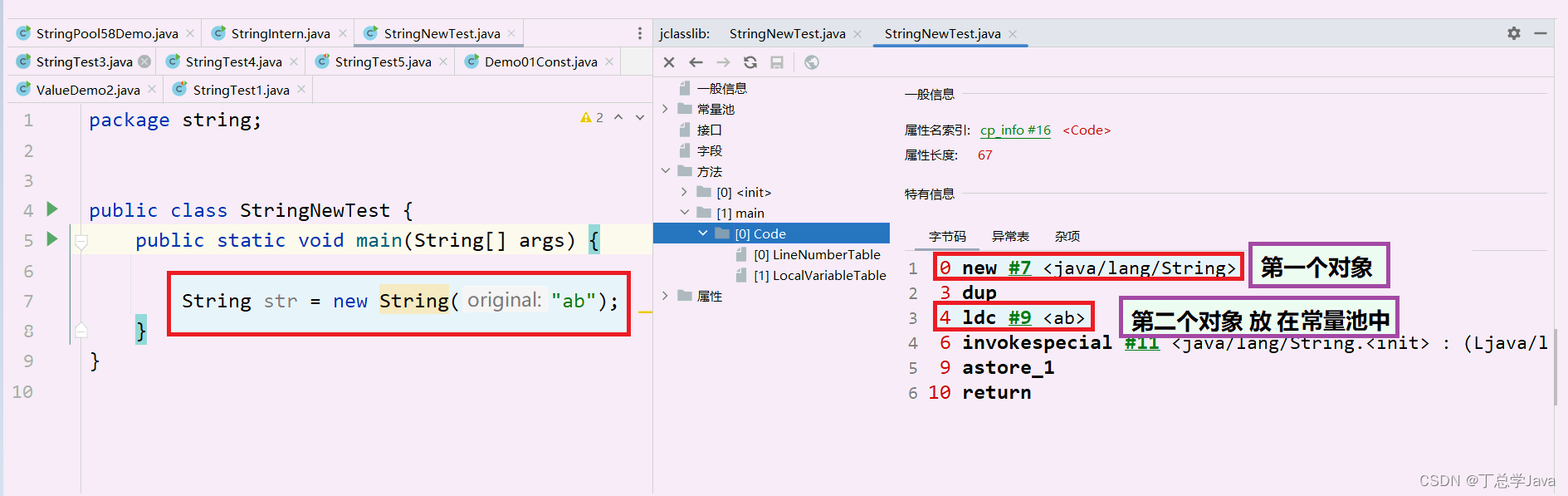
new String()到底创建了几个对象
题目: new String("abc")会创建几个对象? 看字节码,就知道是两个。...

第五十五天
CSS3 ●背景 CSS3 中包含几个新的背景属性,提供更大背景元素控制: •background-image:添加背景图片。不同的背景图像和图像用逗号隔开,所有的图片中显示在最顶端的为第一张。 •background-size:指定背景图像的大…...

【推荐】深入浅出benan的生命周期
目录 1.spring 管理JavaBean的过程(生命周期) 2.spring的JavaBean管理中单例模式及原型(多例)模式 2.1 . 默认为单例,但是可以配置多例 2.2.举例论证 2.2.1 默认单例 2.2.2 设置多例 2.2.3单例与多例的初始化的时…...
mysql使用redis+canal实现缓存一致性
目录 一、开启binlog日志 1.首先查看是否开启了binlog 2、开启binlog日志,并重启mysql服务 二、授权 canal 链接 MySQL 账号具有作为 MySQL slave 的权限 三、下载配置canal 1、下载 canal, 访问 release 页面 , 选择需要的包下载, 如以 1.0.17 版本为例 2、 …...
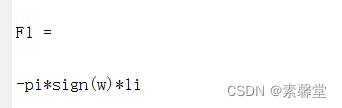
9.利用matlab完成 泰勒级数展开 和 符号表达式傅里叶变换和反变换 (matlab程序)
1.简述 matlab之傅里叶变换和逆变换 首先生成一个方波(或者其他组合波形),然后对这个信号做傅里叶变换,拆解到频域,可以看到这个信号是由哪些频率的信号叠加而来。 然后把频域信号,用傅里叶逆变换恢复到时…...

文字点选验证码识别(上)-YOLO位置识别
声明 本文以教学为基准、本文提供的可操作性不得用于任何商业用途和违法违规场景。 本人对任何原因在使用本人中提供的代码和策略时可能对用户自己或他人造成的任何形式的损失和伤害不承担责任。 如有侵权,请联系我进行删除。 文章中没有代码,只有过程思路,请大家谨慎订阅。…...

ssh远程连接慢解决方法
一、关闭SERVER上的GSS认证 将GSSAPIAuthentication改为no ,如果在配置文件中,以下值是被注释的就拿掉注释,因为默认开关就是yes # vi /etc/ssh/sshd_config GSSAPIAuthentication no二、关闭SERVER上DNS反向解析 在linux中,默认就是开启了S…...
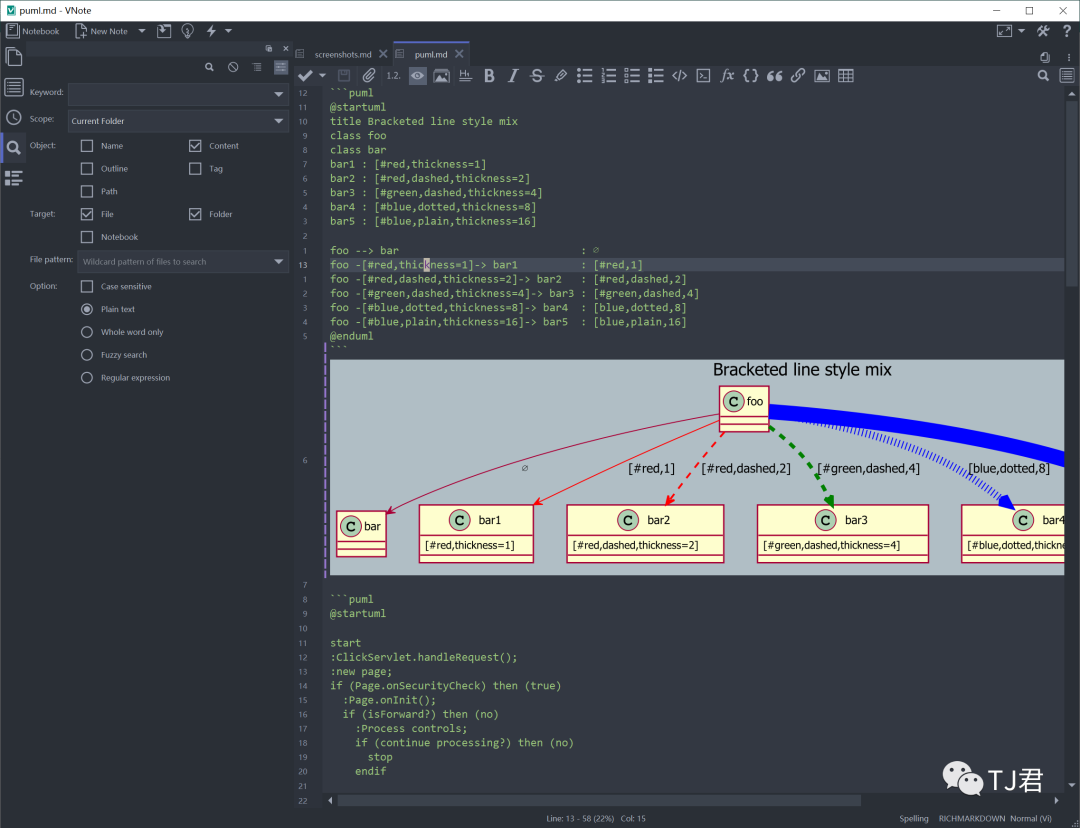
10.4K Star!程序员为程序员针对性优化的开源免费笔记
平时我一直用Notion来记录内容为主,但也一直关注着其他开源产品。上周正好看到一款非常受欢迎的开源免费笔记,今天就推荐给大家:VNote。 VNote一个由程序员为程序员打造的开源笔记应用,基于Qt开发,专注于使用 Markdown…...
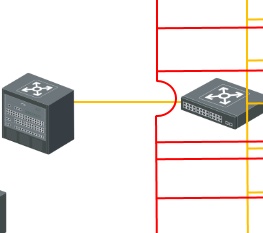
ppt中线材相交接的地方,如何绘画
ppt中线材相交接的地方: 在ppt中绘画线材相互交接的地方: 1.1绘图工具中的“弧形” 1.2小技巧 “弧形”工具点一下,在ppt中如下 1.3拖动活动点进行调整图形 1.4绘画圆弧 1.5调整“圆弧”的大小,鼠标放在“黄色点”位置…...
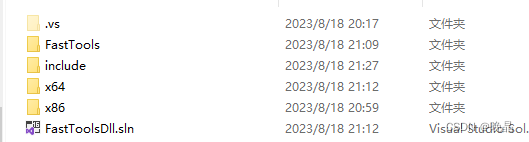
[VS/C++]如何更好的配置DLL项目中的成品输出
注意,解决方案与项目不放在同一个文件夹中,即不选中图中选项 直入主题 首先右键项目选择属性,或者选中项目然后AltEnter 选择配置属性下的常规 分别在四种配置中编辑输出目录如下 注意,四种配置要分别配置,一个个来…...

REC 系列 Visual Grounding with Transformers 论文阅读笔记
REC 系列 Visual Grounding with Transformers 论文阅读笔记 一、Abstract二、引言三、相关工作3.1 视觉定位3.2 视觉 Transformer 四、方法4.1 基础的视觉和文本编码器4.2 定位编码器自注意力的文本分支文本引导自注意力的视觉分支 4.3 定位解码器定位 query 自注意力编码器-解…...

Linux常用命令总结
Linux是一种自由和开放源代码的操作系统,它被广泛用于服务器和其他大型系统中。然而,如果你刚开始使用Linux,可能会对如何有效地操作感到困惑。这篇文章将介绍一些常用的Linux命令,帮助你更好地理解和使用这个强大的系统。 文件和…...
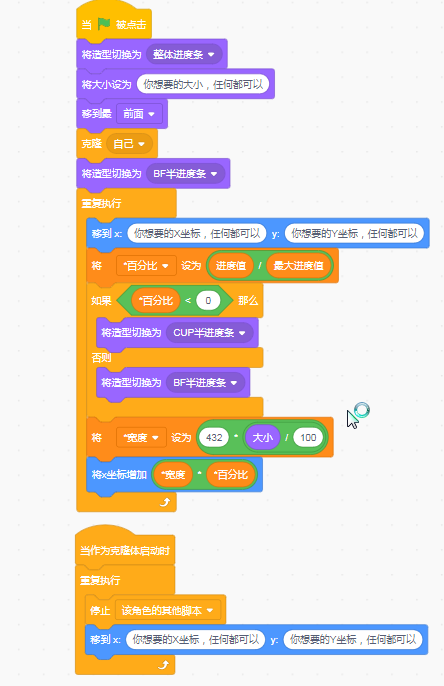
Scratch 之 制作超丝滑 FNF 推条
这个教程是不用画笔的,所以不用担心推条是最后一层了! 导入素材 你以为真是这样吗?NO,NO,NO,其实是这样的 没错,中间是空的!中间是空的!中间是空的!…...

java通过反射,动态调用指定注解的方法
SpringBootTest RunWith(SpringRunner.class) public class AnnoTest {Autowiredprivate ApplicationContext applicationContext;Testpublic void test(){// 获取有指定注解的BeanMap<String, Object> annotationMap applicationContext.getBeansWithAnnotation(CacheC…...

QT学习方法
1 .类的学习方法 第一步:从UI文件中,找到界面的类—QMainWindow第二步:在Qt Creator工具中,找到“帮助”按钮,进入到帮助菜单界面,在选择"索引",在Look for:输入类名,找到类名,双击条目中的类名,在右侧会显示出来类的详细内容第三步:在右侧,可根据内容目录…...

C++中的类型擦除技术
文章目录 一、C类型擦除Type Erasure技术1.虚函数2.模板和函数对象 二、任务队列1.基于特定类型的方式实现2.基于任意类型的方式实现 参考: 一、C类型擦除Type Erasure技术 C中的类型擦除(Type Erasure)是一种技术,用于隐藏具体类…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...
LINUX编译vlc
下载 VideoLAN / VLC GitLab 选择最新的发布版本 准备 sudo apt install -y xcb bison sudo apt install -y autopoint sudo apt install -y autoconf automake libtool编译ffmpeg LINUX FFMPEG编译汇总(最简化)_底部的附件列表中】: ffmpeg - lzip…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...
