169. 多数元素(摩尔投票法) 题解
题目描述:169. 多数元素 - 力扣(LeetCode)
给定一个大小为
n的数组nums,返回其中的多数元素。多数元素是指在数组中出现次数 大于⌊ n/2 ⌋的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 :
输入:nums = [2,2,1,1,1,2,2] 输出:2
可以使用摩尔投票算法(Boyer-Moore Voting Algorithm)来解决这个问题,它是解决这种类型问题的一种高效算法。它的基本思想是通过不断消除不同元素对的投票来找到出现次数最多的元素。
-
摩尔投票算法
对于数组来说,数组中的每一个元素代表一个候选人,该数字出现的次数就是这个候选人的得票数,当候选人的投票数超过总票数的一半时,该候选人就能当选,也就找到了出现次数超过一半的数字:

算法思想:
因为各个候选人的关系是相互对立的,所以对于相互对立的得票可以相互抵消:
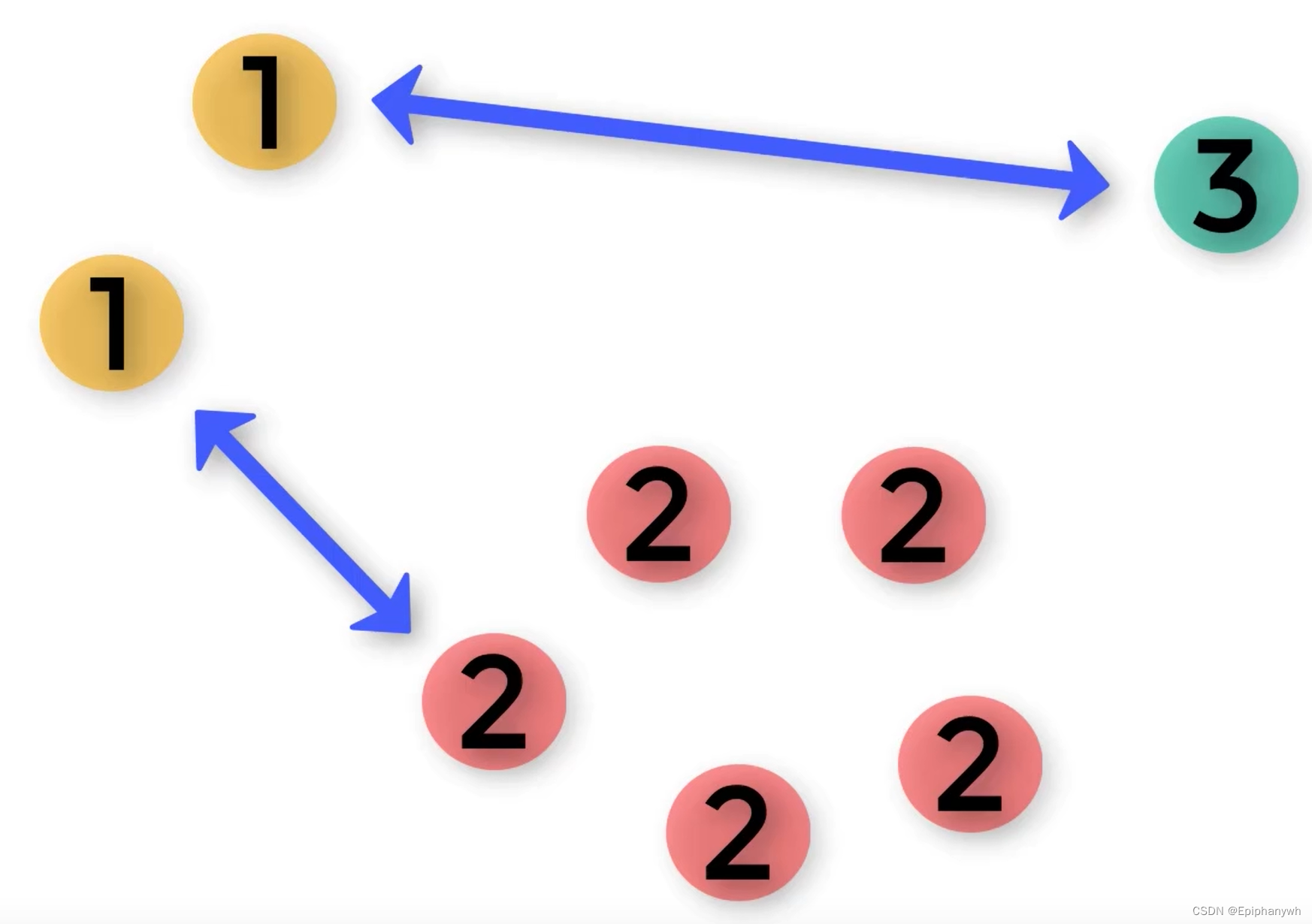

抵消到最后,还有票数的候选人就是当选人了。
当然,对立情况可能不是上面的那种情况:


显然,在这种情况下,也可以找到当选人,所以这个算法是合理的。
但是如果只是这样做,只能找到出现次数最多的数字,而这个数字出现的次数不一定超过一半,所以找到出现次数最多的数字后,还要再进行遍历判断出现次数是否超过一半。
让我通过一个实例来解释这个情况。假设数组为:
[3, 1, 3, 1, 2, 1, 2]。使用摩尔投票算法进行步骤演示:
- 初始化候选元素
candidate = 3,计数count = 1。- 遍历到元素
1,与候选元素不同,计数减1,count = 0。- 更新候选元素为
1,计数为1。- 遍历到元素
3,与候选元素不同,计数减1,count = 0。- 更新候选元素为
3,计数为1。- 遍历到元素
1,与候选元素不同,计数减1,count = 0。- 更新候选元素为
1,计数为1。- 遍历到元素
2,与候选元素不同,计数减1,count = 0。- 更新候选元素为
2,计数为1。在这个例子中,最后剩下的候选元素是
2,但是它并不是出现次数超过一半的元素。实际上,数组中没有出现次数超过一半的元素,因此摩尔投票算法无法在这种情况下找到多数元素。这正是为什么要在算法的最后一步进行验证的原因。通过验证候选元素的实际出现次数,我们可以确保它是否真的是多数元素。如果验证通过,那么候选元素就是多数元素;如果验证不通过,说明数组中没有多数元素。
在摩尔投票算法的应用中,验证是确保算法正确性的重要一步,尤其是在出现没有多数元素的情况下。
实现摩尔投票算法的具体步骤如下:
-
初始化候选元素和计数: 首先,初始化两个变量,一个用来存储候选元素(
candidate),另一个用来存储候选元素的计数(count)。初始时,将候选元素设为数组的第一个元素,将计数设为1。 -
遍历数组: 从数组的第二个元素开始,遍历整个数组。
- 如果当前元素与候选元素相同,将计数加1。
- 如果当前元素与候选元素不同,将计数减1。
-
更新候选元素: 在每次计数减到0时,说明之前的候选元素和其他元素抵消掉了,需要选择新的候选元素。此时,将当前元素作为新的候选元素,将计数重新设为1。
-
验证候选元素: 遍历完数组后,得到的候选元素可能是多数元素,但也可能不是。为了验证候选元素是否确实是多数元素,再次遍历整个数组,统计候选元素的实际出现次数。
-
确定多数元素: 如果候选元素的实际出现次数大于数组长度的一半(即超过 ⌊ n/2 ⌋ 次),则该候选元素可以被确认为多数元素;否则,说明没有多数元素存在。
用C语言实现的代码如下:
int majorityElement(int* nums, int numsSize) {int candidate = 0;int count = 0;for (int i = 0; i < numsSize; i++) {if (count == 0) {candidate = nums[i];count = 1;} else if (nums[i] == candidate) {count++;} else {count--;}}// 验证候选元素是否为多数元素count = 0;for (int i = 0; i < numsSize; i++) {if (nums[i] == candidate) {count++;}}if (count > numsSize / 2) {return candidate;}// 实际上,题目保证了一定存在多数元素,所以不会执行到这里return -1;
}注:摩尔算法不仅可以用来找到目标数字,如果目标元素是字符也是可以用该算法解题的。
本次内容到此结束了!如果你觉得这篇博客对你有帮助的话 ,希望你能够给我点个赞,鼓励一下我。感谢感谢……
参考资料:
【【算法】摩尔投票法】https://www.bilibili.com/video/BV1Co4y1y7LL?vd_source=564abed1c36a31978eb9de7cdc6668d2
相关文章:

169. 多数元素(摩尔投票法) 题解
题目描述:169. 多数元素 - 力扣(LeetCode) 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示…...

python中的cnn:介绍和基本使用方法
python中的cnn:介绍和基本使用方法 卷积神经网络(Convolutional Neural Networks,简称CNN)是一种在图像识别、语音识别、自然语言处理等许多领域取得显著成功的深度学习模型。CNN的设计灵感来源于生物的视觉系统,由多…...
Dockerfile概念、镜像原理、制作及案例讲解
1.Docker镜像原理 Linux文件操作系统讲解 2.镜像如何制作 3.Dockerfile概念 Docker网址:https://hub.docker.com 3.1 Dockerfile关键字 4.案例...

07-微信小程序-注册页面-模块化
07-微信小程序-注册页面 文章目录 注册页面使用 Page 构造器注册页面参数Object初始数据案例代码 生命周期回调函数组件事件处理函数setData()案例代码 生命周期模块化 注册页面 对于小程序中的每个页面,都需要在页面对应的 js 文件中进行注册,指定页面…...
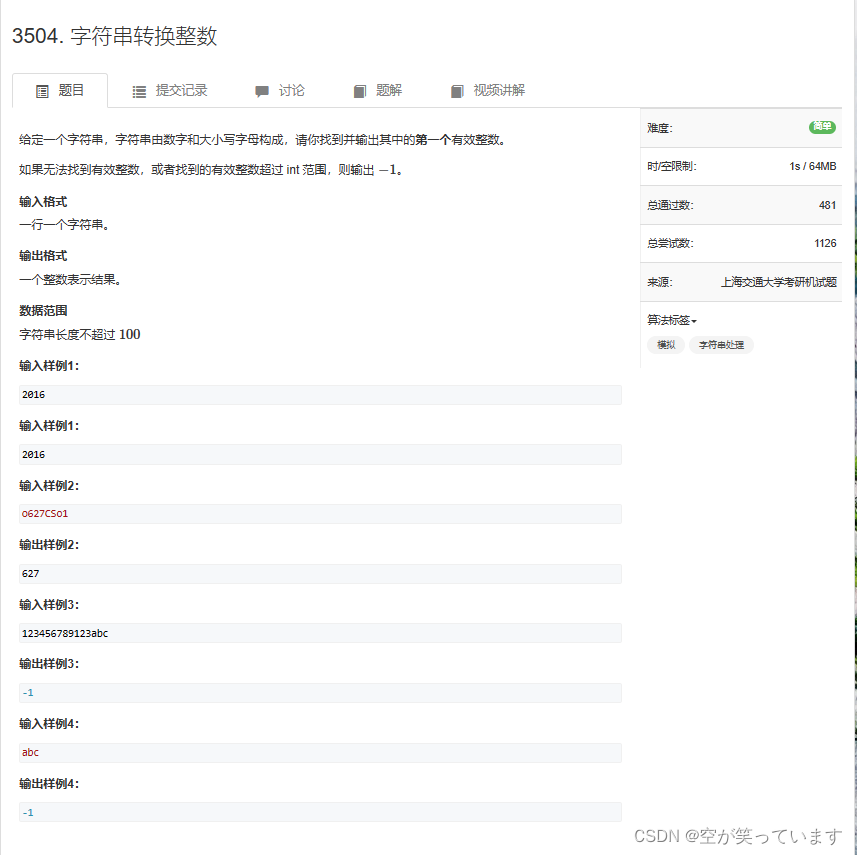
考研算法第46天: 字符串转换整数 【字符串,模拟】
题目前置知识 c中的string判空 string Count; Count.empty(); //正确 Count ! null; //错误c中最大最小宏 #include <limits.h>INT_MAX INT_MIN 字符串使用发运算将字符加到字符串末尾 string Count; string str "liuda"; Count str[i]; 题目概况 AC代码…...

Cesium for unity 1.5.0使用注意事项
Cesium for Unity Quickstart – Cesium 1.Unity版本仅支持Unity2021.3.2f1以后版 2.仅支持 3D (URP)和3D (HDRP)渲染管线 3.如果Package Manager中不出现My Registries选项,请在 Edit > Project Settings...>Package Manager中重命名或删除重新添加Packag…...

初阶C语言-结构体
🌞 “少年有梦不至于心动,更要付诸行动。” 今天我们一起学习一下结构体的相关内容! 结构体 🎈1.结构体的声明1.1结构的基础知识1.2结构的声明1.3结构成员的类型1.4结构体变量的定义和初始化 🎈2.结构体成员的访问2.1结…...

Android Studio实现解析HTML获取图片URL,将URL存到list,进行瀑布流展示
目录 效果展示build.gradle(app)添加的依赖(用不上的可以不加)AndroidManifest.xml错误代码activity_main.xmlitem_image.xmlMainActivityImage适配器ImageModel 接收图片URL效果展示 build.gradle(app)添加的依赖(用不上的可以不加) dependencies {implementation co…...
java学习004
常用数据结构对应 php中常用的数据结构是Array数组,相对的在java开发中常用的数据结构是ArrayList和HashMap,它们可以看成是array的拆分,一种简单的对应关系为 PHPJAVAArray: array(1,2,3)ArrayListlArray: array(“name” > “jack”,“…...
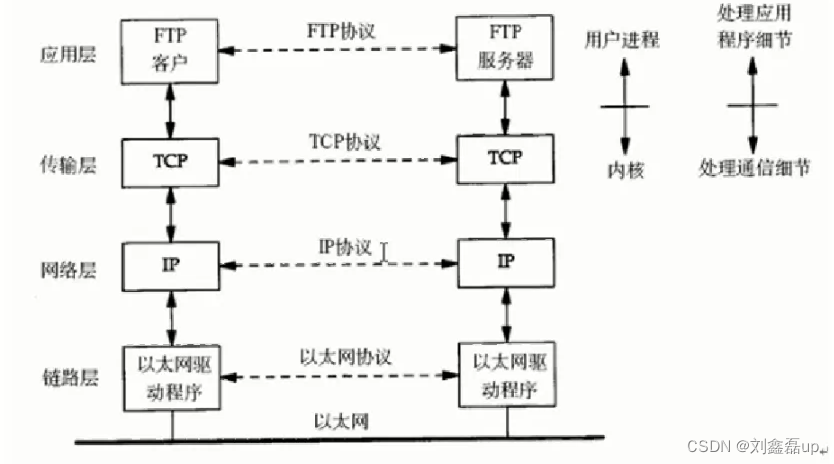
Linux网络编程:网络基础
文章目录: 1.协议 2.锁 3.网络层次模型 4.以太网帧和ARP协议 5.IP协议 6.UDP协议 7.TCP协议 8.BS模式和CS模式 9.网络套接字(socket) 10.网络字节序 11.IP地址转换函数 12.sockaddr地址结构 学习Linux的网络编程原则上基于:Linux的系统编程…...
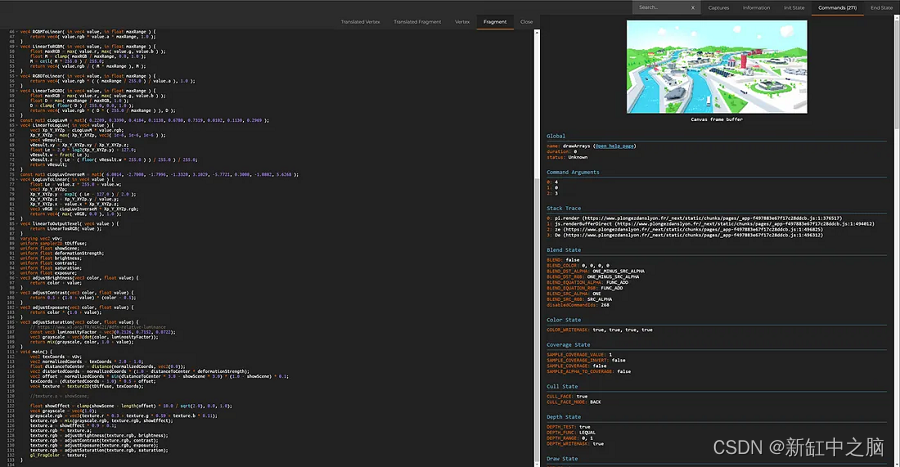
3D沉浸式旅游网站开发案例复盘【Three.js】
Plongez dans Lyon网站终于上线了。 我们与 Danka 团队和 Nico Icecream 共同努力,打造了一个令我们特别自豪的流畅的沉浸式网站。 这个网站是专为 ONLYON Tourism 和会议而建,旨在展示里昂最具标志性的活动场所。观看简短的介绍视频后,用户…...

IO的几个模型
I/O模型名词介绍 说到I/O模型,都会牵扯到同步、异步、阻塞、非阻塞这几个词,以下讲解这几个词的概念。 阻塞和非阻塞 阻塞和非阻塞指的是一直等还是可以去做其他事。 阻塞(blocking):调用结果返回之前,…...

中路对线发现正在攻防演练中投毒的红队大佬
背景 2023年8月14日晚,墨菲安全实验室发布《首起针对国内金融企业的开源组件投毒攻击事件》NPM投毒事件分析文章,紧接着我们在8月17日监控到一个新的npm投毒组件包 hreport-preview,该投毒组件用来下载木马文件的域名地址竟然是 img.murphys…...

【LINUX相关】生成随机数(srand、/dev/random 和 /dev/urandom )
目录 一、问题背景二、修改方法2.1 修改种子2.2 使用linux中的 /dev/urandom 生成随机数 三、/dev/random 和 /dev/urandom 的原理3.1 参考连接3.2 重难点总结3.2.1 生成随机数的原理3.2.2 随机数生成器的结构3.2.3 二者的区别和选择 四、在代码的使用方法 一、问题背景 在一个…...

spark使用心得
spark入门 启停spark sbin/start-all.shsbin/stop-all.shspark-shell 进入spark/bin目录,执行: ./spark-shell 输出中有这么一行: Spark context Web UI available at http://xx.xx.xx.188:4040意味着我们可以从web页面查看spark的运行情…...

什么是边车
名词和概念定义 Sidecar:边车。微服务中数据平面的进程,负责转发应用、服务请求,并支持限流、熔断、负载均衡等特性。 Control-plane: 控制平面。微服务的配置中心,负责配置下发、数据搜集、服务发现等功能。 应用: 应用是指服务…...

vue项目打包成exe文件
1. 获取electron-quick-start demo git clone https://github.com/electron/electron-quick-start2. 安装依赖包 npm install 或 npm i // 安装依赖时可能会遇到node版本的问题,需要切换node版本的可以先看下nvm,简单易操作3. 打包项目(需要…...

基于MFCC特征提取和GMM训练的语音信号识别matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1 MFCC特征提取 4.2 Gaussian Mixture Model(GMM) 4.3. 实现过程 4.4 应用领域 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3…...
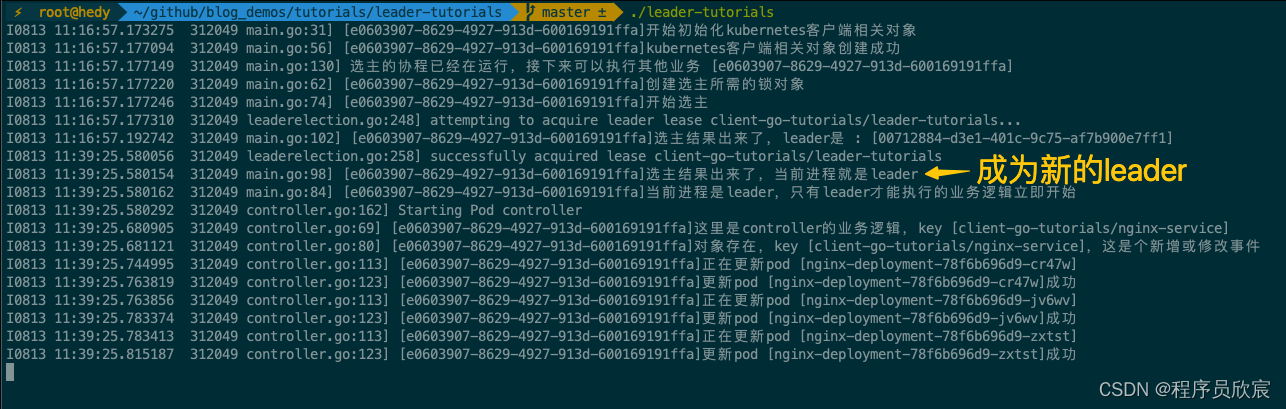
client-go实战之十二:选主(leader-election)
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 本文是《client-go实战》系列的第十二篇,又有一个精彩的知识点在本章呈现:选主(leader-election)在解释什么是选主之前&…...
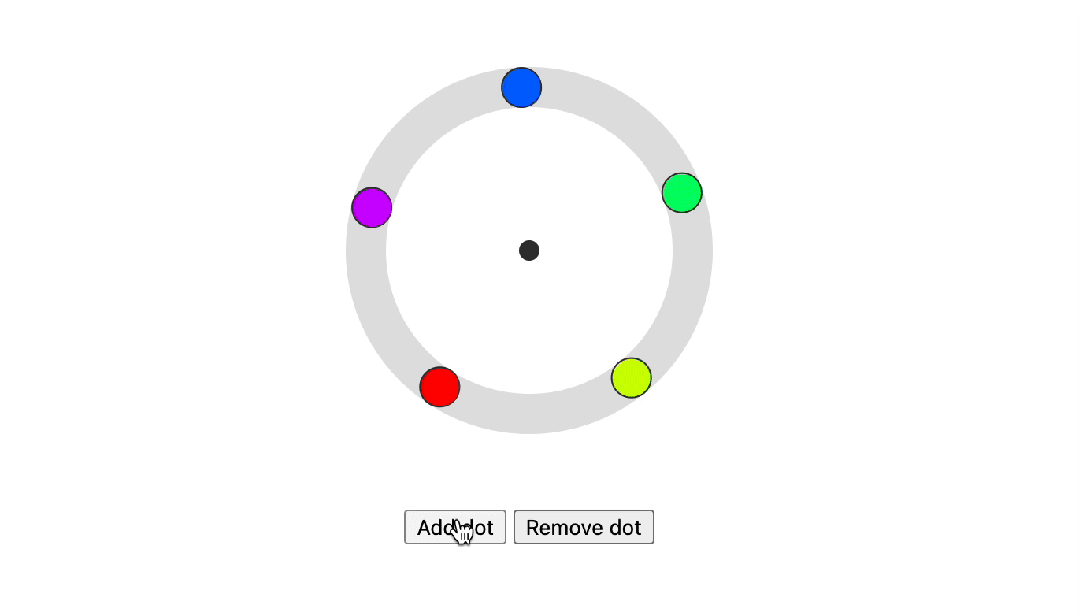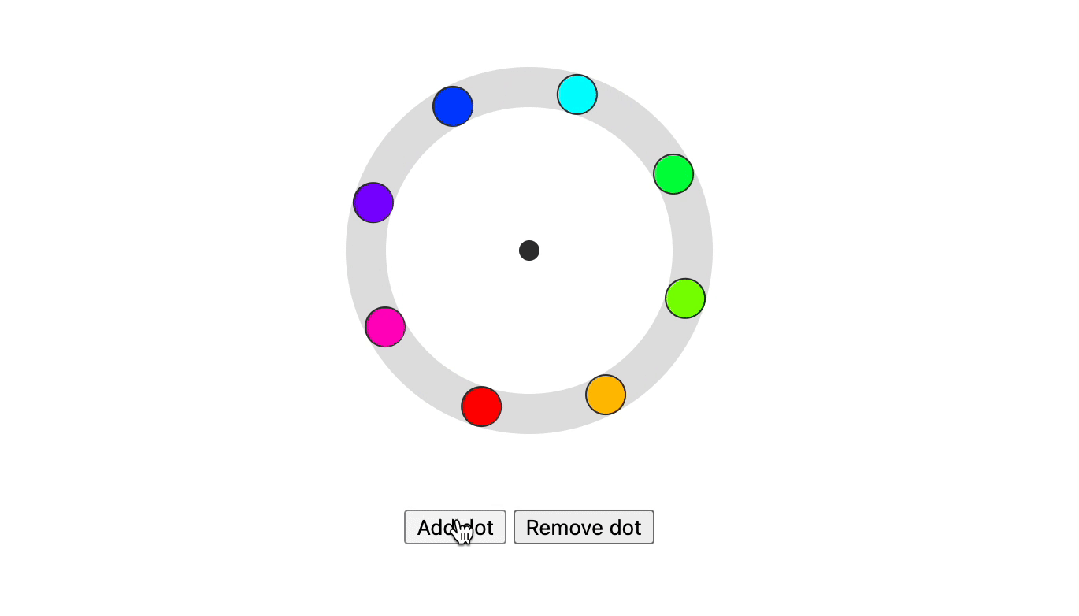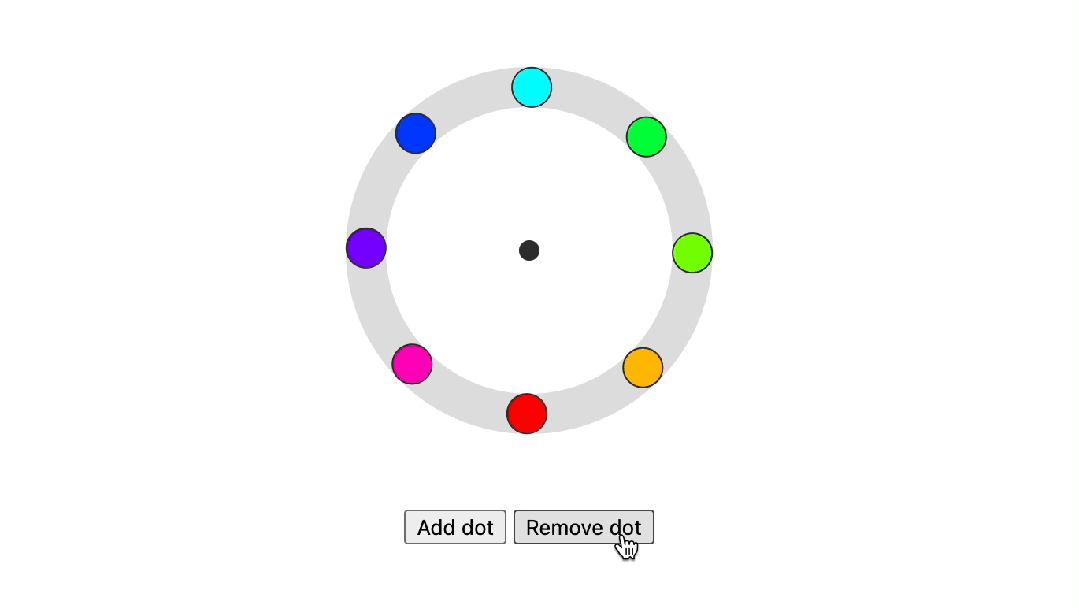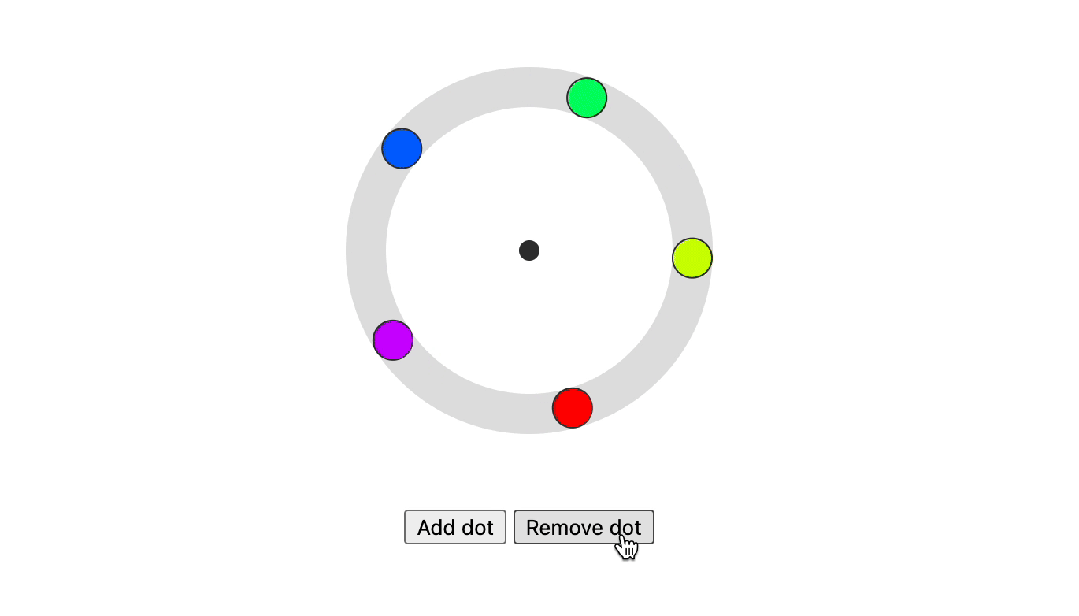
2023年即将推出的CSS特性对你影响大不大?
Google开发者大会每年都会提出有关于 Web UI 和 CSS 方面的新特性,今年又上新了许多新功能,今天就从中找出了影响最大的几个功能给大家介绍一下 :has :has() 可以通过检查父元素是否包含特定子元素或这些子元素是否处于特定状态来改变样式,也…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...

Docker 镜像上传到 AWS ECR:从构建到推送的全流程
一、在 EC2 实例中安装 Docker(适用于 Amazon Linux 2) 步骤 1:连接到 EC2 实例 ssh -i your-key.pem ec2-useryour-ec2-public-ip步骤 2:安装 Docker sudo yum update -y sudo amazon-linux-extras enable docker sudo yum in…...

基于微信小程序的作业管理系统源码数据库文档
作业管理系统 摘 要 随着社会的发展,社会的方方面面都在利用信息化时代的优势。互联网的优势和普及使得各种系统的开发成为必需。 本文以实际运用为开发背景,运用软件工程原理和开发方法,它主要是采用java语言技术和微信小程序来完成对系统的…...
