数据结构的树存储结构
数据结构的树存储结构
之前介绍的所有的数据结构都是线性存储结构。本章所介绍的树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合。
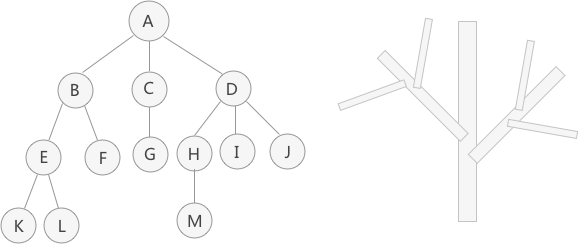
(A) (B)
图 1 树的示例
图 1(A) 是使用树结构存储的集合 {A,B,C,D,E,F,G,H,I,J,K,L,M} 的示意图。对于数据 A 来说,和数据 B、C、D 有关系;对于数据 B 来说,和 E、F 有关系。这就是“一对多”的关系。
将具有“一对多”关系的集合中的数据元素按照图 1(A)的形式进行存储,整个存储形状在逻辑结构上看,类似于实际生活中倒着的树(图 1(B)倒过来),所以称这种存储结构为“树型”存储结构。
树的结点
结点:使用树结构存储的每一个数据元素都被称为“结点”。例如,图 1(A)中,数据元素 A 就是一个结点;
父结点(双亲结点)、子结点和兄弟结点:对于图 1(A)中的结点 A、B、C、D 来说,A 是 B、C、D 结点的父结点(也称为“双亲结点”),而 B、C、D 都是 A 结点的子结点(也称“孩子结点”)。对于 B、C、D 来说,它们都有相同的父结点,所以它们互为兄弟结点。
树根结点(简称“根结点”):每一个非空树都有且只有一个被称为根的结点。图 1(A)中,结点 A 就是整棵树的根结点。
树根的判断依据为:如果一个结点没有父结点,那么这个结点就是整棵树的根结点。
叶子结点:如果结点没有任何子结点,那么此结点称为叶子结点(叶结点)。例如图 1(A)中,结点 K、L、F、G、M、I、J 都是这棵树的叶子结点。
子树和空树
子树:如图 1(A)中,整棵树的根结点为结点 A,而如果单看结点 B、E、F、K、L 组成的部分来说,也是棵树,而且节点 B 为这棵树的根结点。所以称 B、E、F、K、L 这几个结点组成的树为整棵树的子树;同样,结点 E、K、L 构成的也是一棵子树,根结点为 E。
注意:单个结点也是一棵树,只不过根结点就是它本身。图 1(A)中,结点 K、L、F 等都是树,且都是整棵树的子树。
知道了子树的概念后,树也可以这样定义:树是由根结点和若干棵子树构成的。
空树:如果集合本身为空,那么构成的树就被称为空树。空树中没有结点。
补充:在树结构中,对于具有同一个根结点的各个子树,相互之间不能有交集。例如,图 1(A)中,除了根结点 A,其余元素又各自构成了三个子树,根结点分别为 B、C、D,这三个子树相互之间没有相同的结点。如果有,就破坏了树的结构,不能算做是一棵树。
结点的度和层次
对于一个结点,拥有的子树数(结点有多少分支)称为结点的度(Degree)。例如,图 1(A)中,根结点 A 下分出了 3 个子树,所以,结点 A 的度为 3。
一棵树的度是树内各结点的度的最大值。图 1(A)表示的树中,各个结点的度的最大值为 3,所以,整棵树的度的值是 3。
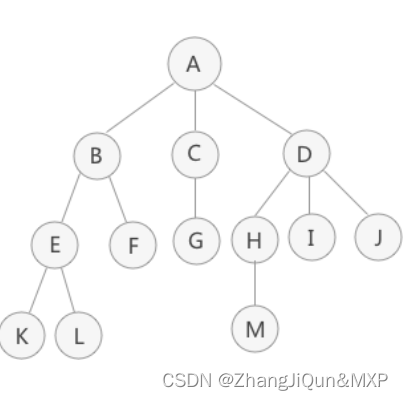
结点的层次:从一棵树的树根开始,树根所在层为第一层,根的孩子结点所在的层为第二层,依次类推。对于图 1(A)来说,A 结点在第一层,B、C、D 为第二层,E、F、G、H、I、J 在第三层,K、L、M 在第四层。
一棵树的深度(高度)是树中结点所在的最大的层次。图 1(A)树的深度为 4。
如果两个结点的父结点虽不相同,但是它们的父结点处在同一层次上,那么这两个结点互为堂兄弟。例如,图 1(A)中,结点 G 和 E、F、H、I、J 的父结点都在第二层,所以之间为堂兄弟的关系。
有序树和无序树
如果树中结点的子树从左到右看,谁在左边,谁在右边,是有规定的,这棵树称为有序树;反之称为无序树。
在有序树中,一个结点最左边的子树称为"第一个孩子",最右边的称为"最后一个孩子"。
拿图 1(A)来说,如果是其本身是一棵有序树,则以结点 B 为根结点的子树为整棵树的第一个孩子,以结点 D 为根结点的子树为整棵树的最后一个孩子。
森林
由 m(m >= 0)个互不相交的树组成的集合被称为森林。图 1(A)中,分别以 B、C、D 为根结点的三棵子树就可以称为森林。
前面讲到,树可以理解为是由根结点和若干子树构成的,而这若干子树本身是一个森林,所以,树还可以理解为是由根结点和森林组成的。用一个式子表示为:
Tree =(root,F)
其中,root 表示树的根结点,F 表示由 m(m >= 0)棵树组成的森林。
树的表示方法
除了图 1(A)表示树的方法外,还有其他表示方法:

(A) (B)
图2 树的表示形式
图 2(A)是以嵌套的集合的形式表示的(集合之间绝不能相交,即图中任意两个圈不能相交)。
图 2(B)使用的是凹入表示法(了解即可),表示方式是:最长条为根结点,相同长度的表示在同一层次。例如 B、C、D 长度相同,都为 A 的子结点,E 和 F 长度相同,为 B 的子结点,K 和 L 长度相同,为 E 的子结点,依此类推。
最常用的表示方法是使用广义表的方式。图 1(A)用广义表表示为:
(A , ( B ( E ( K , L ) , F ) , C ( G ) , D ( H ( M ) , I , J ) ) )
总结
树型存储结构类似于家族的族谱,各个结点之间也同样可能具有父子、兄弟、表兄弟的关系。本节中,要重点理解树的根结点和子树的定义,同时要会计算树中各个结点的度和层次,以及树的深度。
什么是二叉树(包含满二叉树和完全二叉树)
简单地理解,满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
例如,图 1a) 就是一棵二叉树,而图 1b) 则不是。
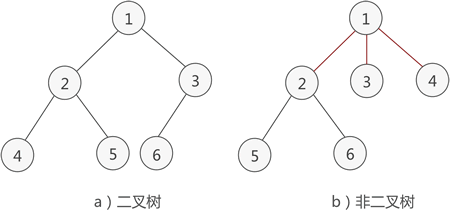
图 1 二叉树示意图
二叉树的性质
经过前人的总结,二叉树具有以下几个性质:
- 二叉树中,第 i 层最多有 2i-1 个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
性质 3 的计算方法为:对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n1),那么总结点 n=n0+n1+n2。
同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B=n1+2*n2。所以,n 用另外一种方式表示为 n=n1+2*n2+1。
两种方式得到的 n 值组成一个方程组,就可以得出 n0=n2+1。
二叉树还可以继续分类,衍生出满二叉树和完全二叉树。
满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
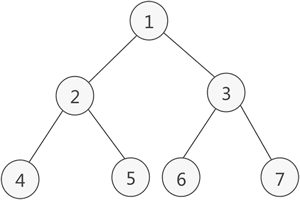
图 2 满二叉树示意图
如图 2 所示就是一棵满二叉树。
满二叉树除了满足普通二叉树的性质,还具有以下性质:
- 满二叉树中第 i 层的节点数为 2n-1 个。
- 深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
- 满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
- 具有 n 个节点的满二叉树的深度为 log2(n+1)。
完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
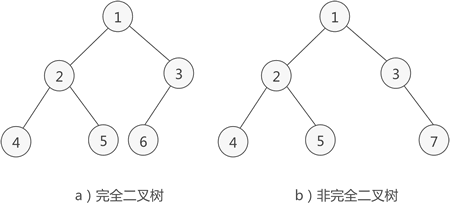
图 3 完全二叉树示意图
如图 3a) 所示是一棵完全二叉树,图 3b) 由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树。
完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
⌊log2n⌋ 表示取小于 log2n 的最大整数。例如,⌊log24⌋ = 2,而 ⌊log25⌋ 结果也是 2。
对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号(如图 3a)),对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
- 当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
- 如果 2*i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2*i 。
- 如果 2*i+1>n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2*i+1 。
二叉树的顺序存储结构(看了无师自通)
二叉树的存储结构有两种,分别为顺序存储和链式存储。本节先介绍二叉树的顺序存储结构。
二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
有读者会说,满二叉树也可以使用顺序存储。要知道,满二叉树也是完全二叉树,因为它满足完全二叉树的所有特征。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如图 1 所示:
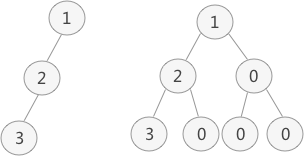
图 1 普通二叉树的转化
图 1 中,左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
解决了二叉树的转化问题,接下来学习如何顺序存储完全(满)二叉树。
完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。
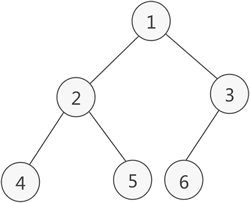
图 2 完全二叉树示意图
例如,存储图 2 所示的完全二叉树,其存储状态如图 3 所示:

图 3 完全二叉树存储状态示意图
同样,存储由普通二叉树转化来的完全二叉树也是如此。例如,图 1 中普通二叉树的数组存储状态如图 4 所示:

图 4 普通二叉树的存储状态
由此,我们就实现了完全二叉树的顺序存储。
不仅如此,从顺序表中还原完全二叉树也很简单。我们知道,完全二叉树具有这样的性质,将树中节点按照层次并从左到右依次标号(1,2,3,...),若节点 i 有左右孩子,则其左孩子节点为 2*i,右孩子节点为 2*i+1。此性质可用于还原数组中存储的完全二叉树,也就是实现由图 3 到图 2、由图 4 到图 1 的转变。
二叉树的链式存储结构(C语言详解)
本节我们学习二叉树的链式存储结构。
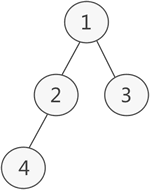
图 1 普通二叉树示意图
如图 1 所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。因此,图 1 对应的链式存储结构如图 2 所示:
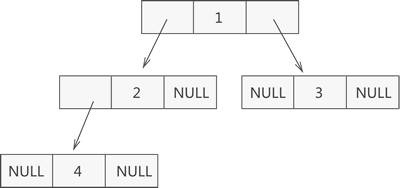
图 2 二叉树链式存储结构示意图
由图 2 可知,采用链式存储二叉树时,其节点结构由 3 部分构成(如图 3 所示):
- 指向左孩子节点的指针(Lchild);
- 节点存储的数据(data);
- 指向右孩子节点的指针(Rchild);

图 3 二叉树节点结构
表示该节点结构的 C 语言代码为:
- typedef struct BiTNode{
- TElemType data;//数据域
- struct BiTNode *lchild,*rchild;//左右孩子指针
- struct BiTNode *parent;
- }BiTNode,*BiTree;
图 2 中的链式存储结构对应的 C 语言代码为:
- #include <stdio.h>
- #include <stdlib.h>
- #define TElemType int
- typedef struct BiTNode{
- TElemType data;//数据域
- struct BiTNode *lchild,*rchild;//左右孩子指针
- }BiTNode,*BiTree;
- void CreateBiTree(BiTree *T){
- *T=(BiTNode*)malloc(sizeof(BiTNode));
- (*T)->data=1;
- (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
- (*T)->lchild->data=2;
- (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
- (*T)->rchild->data=3;
- (*T)->rchild->lchild=NULL;
- (*T)->rchild->rchild=NULL;
- (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
- (*T)->lchild->lchild->data=4;
- (*T)->lchild->rchild=NULL;
- (*T)->lchild->lchild->lchild=NULL;
- (*T)->lchild->lchild->rchild=NULL;
- }
- int main() {
- BiTree Tree;
- CreateBiTree(&Tree);
- printf("%d",Tree->lchild->lchild->data);
- return 0;
- }
程序输出结果:
4
其实,二叉树的链式存储结构远不止图 2 所示的这一种。例如,在某些实际场景中,可能会做 "查找某节点的父节点" 的操作,这时可以在节点结构中再添加一个指针域,用于各个节点指向其父亲节点,如图 4 所示:
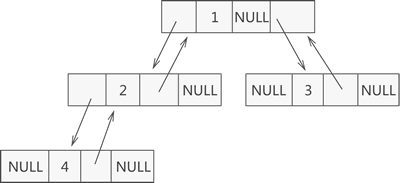
图 4 自定义二叉树的链式存储结构
这样的链表结构,通常称为三叉链表。
利用图 4 所示的三叉链表,我们可以很轻松地找到各节点的父节点。因此,在解决实际问题时,用合适的链表结构存储二叉树,可以起到事半功倍的效果。
树的双亲表示法
普通树结构的数据。
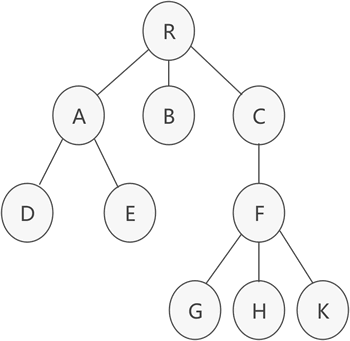
图 1 普通树存储结构
如图 1 所示,这是一棵普通的树,该如何存储呢?通常,存储具有普通树结构数据的方法有 3 种:
- 双亲表示法;
- 孩子表示法;
- 孩子兄弟表示法;
本节先来学习双亲表示法。
双亲表示法采用顺序表(也就是数组)存储普通树,其实现的核心思想是:顺序存储各个节点的同时,给各节点附加一个记录其父节点位置的变量。
注意,根节点没有父节点(父节点又称为双亲节点),因此根节点记录父节点位置的变量通常置为 -1。
例如,采用双亲表示法存储图 1 中普通树,其存储状态如图 2 所示:
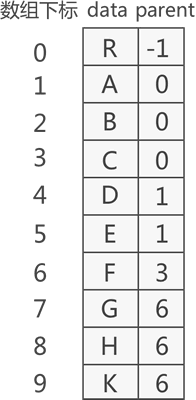
图 2 双亲表示法存储普通树示意图
树的孩子表示法
孩子表示法存储普通树采用的是 "顺序表+链表" 的组合结构,其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。
如果节点没有孩子节点(叶子节点),则该节点的链表为空链表。
例如,使用孩子表示法存储图 1a) 中的普通树,则最终存储状态如图 1b) 所示:
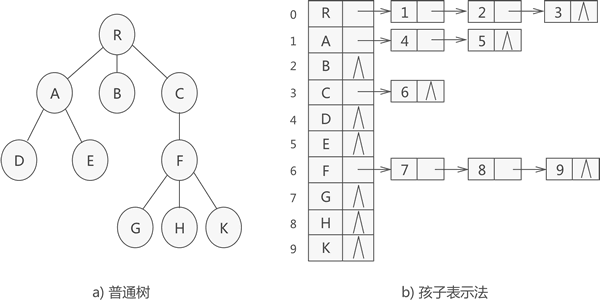
图 1 孩子表示法存储普通树示意图
图 1 所示转化为 C 语言代码为:
- #include<stdio.h>
- #include<stdlib.h>
- #define MAX_SIZE 20
- #define TElemType char
- //孩子表示法
- typedef struct CTNode {
- int child;//链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标
- struct CTNode * next;
- }ChildPtr;
- typedef struct {
- TElemType data;//结点的数据类型
- ChildPtr* firstchild;//孩子链表的头指针
- }CTBox;
- typedef struct {
- CTBox nodes[MAX_SIZE];//存储结点的数组
- int n, r;//结点数量和树根的位置
- }CTree;
- //孩子表示法存储普通树
- CTree initTree(CTree tree) {
- printf("输入节点数量:\n");
- scanf("%d", &(tree.n));
- for (int i = 0; i < tree.n; i++) {
- printf("输入第 %d 个节点的值:\n", i + 1);
- getchar();
- scanf("%c", &(tree.nodes[i].data));
- tree.nodes[i].firstchild = (ChildPtr*)malloc(sizeof(ChildPtr));
- tree.nodes[i].firstchild->next = NULL;
- printf("输入节点 %c 的孩子节点数量:\n", tree.nodes[i].data);
- int Num;
- scanf("%d", &Num);
- if (Num != 0) {
- ChildPtr * p = tree.nodes[i].firstchild;
- for (int j = 0; j < Num; j++) {
- ChildPtr * newEle = (ChildPtr*)malloc(sizeof(ChildPtr));
- newEle->next = NULL;
- printf("输入第 %d 个孩子节点在顺序表中的位置", j + 1);
- scanf("%d", &(newEle->child));
- p->next = newEle;
- p = p->next;
- }
- }
- }
- return tree;
- }
- void findKids(CTree tree, char a) {
- int hasKids = 0;
- for (int i = 0; i < tree.n; i++) {
- if (tree.nodes[i].data == a) {
- ChildPtr * p = tree.nodes[i].firstchild->next;
- while (p) {
- hasKids = 1;
- printf("%c ", tree.nodes[p->child].data);
- p = p->next;
- }
- break;
- }
- }
- if (hasKids == 0) {
- printf("此节点为叶子节点");
- }
- }
- int main()
- {
- CTree tree;
- for (int i = 0; i < MAX_SIZE; i++) {
- tree.nodes[i].firstchild = NULL;
- }
- tree = initTree(tree);
- //默认数根节点位于数组notes[0]处
- tree.r = 0;
- printf("找出节点 F 的所有孩子节点:");
- findKids(tree, 'F');
- return 0;
- }
程序运行结果为:
输入节点数量:
10
输入第 1 个节点的值:
R
输入节点 R 的孩子节点数量:
3
输入第 1 个孩子节点在顺序表中的位置1
输入第 2 个孩子节点在顺序表中的位置2
输入第 3 个孩子节点在顺序表中的位置3
输入第 2 个节点的值:
A
输入节点 A 的孩子节点数量:
2
输入第 1 个孩子节点在顺序表中的位置4
输入第 2 个孩子节点在顺序表中的位置5
输入第 3 个节点的值:
B
输入节点 B 的孩子节点数量:
0
输入第 4 个节点的值:
C
输入节点 C 的孩子节点数量:
1
输入第 1 个孩子节点在顺序表中的位置6
输入第 5 个节点的值:
D
输入节点 D 的孩子节点数量:
0
输入第 6 个节点的值:
E
输入节点 E 的孩子节点数量:
0
输入第 7 个节点的值:
F
输入节点 F 的孩子节点数量:
3
输入第 1 个孩子节点在顺序表中的位置7
输入第 2 个孩子节点在顺序表中的位置8
输入第 3 个孩子节点在顺序表中的位置9
输入第 8 个节点的值:
G
输入节点 G 的孩子节点数量:
0
输入第 9 个节点的值:
H
输入节点 H 的孩子节点数量:
0
输入第 10 个节点的值:
K
输入节点 K 的孩子节点数量:
0
找出节点 F 的所有孩子节点:G H K
使用孩子表示法存储的树结构,正好和双亲表示法相反,适用于查找某结点的孩子结点,不适用于查找其父结点。
其实,我们还可以将双亲表示法和孩子表示法合二为一,那么图 1a) 中普通树的存储效果如图 2所示:
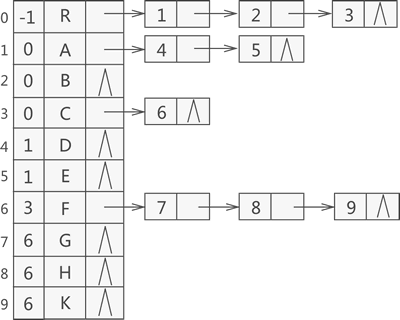
图 2 双亲孩子表示法
使用图 2 结构存储普通树,既能快速找到指定节点的父节点,又能快速找到指定节点的孩子节点。该结构的实现方法很简单,只需整合这两节的代码即可,因此不再赘述。
树的孩子兄弟表示法
一种常用方法——孩子兄弟表示法。
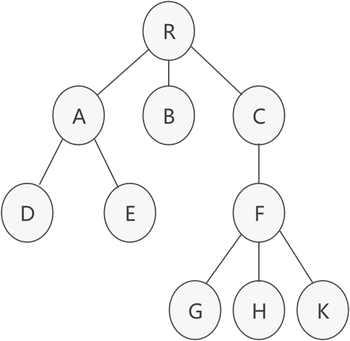
图 1 普通树示意图
树结构中,位于同一层的节点之间互为兄弟节点。例如,图 1 的普通树中,节点 A、B 和 C 互为兄弟节点,而节点 D、E 和 F 也互为兄弟节点。
孩子兄弟表示法,采用的是链式存储结构,其存储树的实现思想是:从树的根节点开始,依次用链表存储各个节点的孩子节点和兄弟节点。
因此,该链表中的节点应包含以下 3 部分内容(如图 2 所示):
- 节点的值;
- 指向孩子节点的指针;
- 指向兄弟节点的指针;
![]()
图 2 节点结构示意图
用 C 语言代码表示节点结构为:
- #define ElemType char
- typedef struct CSNode{
- ElemType data;
- struct CSNode * firstchild,*nextsibling;
- }CSNode,*CSTree;
以图 1 为例,使用孩子兄弟表示法进行存储的结果如图 3 所示:
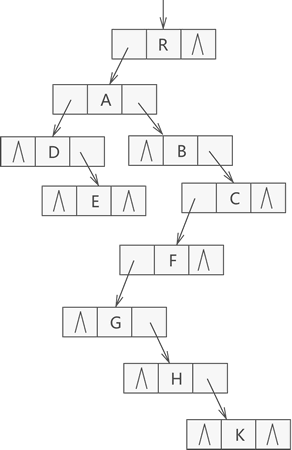
图 3 孩子兄弟表示法示意图
由图 3 可以看到,节点 R 无兄弟节点,其孩子节点是 A;节点 A 的兄弟节点分别是 B 和 C,其孩子节点为 D,依次类推。
实现图 3 中的 C 语言实现代码也很简单,根据图中链表的结构即可轻松完成链表的创建和使用,因此不再给出具体代码。
接下来观察图 1 和图 3。图 1 为原普通树,图 3 是由图 1 经过孩子兄弟表示法转化而来的一棵树,确切地说,图 3 是一棵二叉树。因此可以得出这样一个结论,即通过孩子兄弟表示法,任意一棵普通树都可以相应转化为一棵二叉树,换句话说,任意一棵普通树都有唯一的一棵二叉树于其对应。
因此,孩子兄弟表示法可以作为将普通树转化为二叉树的最有效方法,通常又被称为"二叉树表示法"或"二叉链表表示法"。
相关文章:

数据结构的树存储结构
数据结构的树存储结构 之前介绍的所有的数据结构都是线性存储结构。本章所介绍的树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合。 (A) (B) 图 1 树的示例 图 …...
linux--epoll
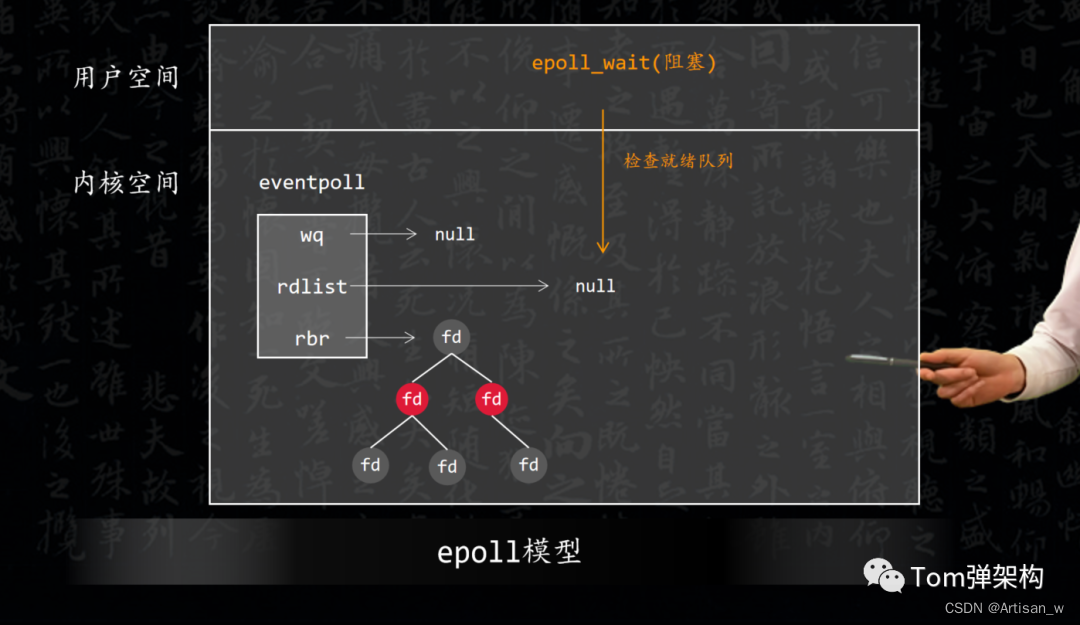
epoll 参考文献 https://www.cnblogs.com/lojunren/p/3856290.html https://www.51cto.com/article/717096.html linux下的I/O复用epoll详解 要深刻理解epoll,首先得了解epoll的三大关键要素:mmap、红黑树、链表。 IO多路复用 首先需要了解什么是IO多…...
async和await
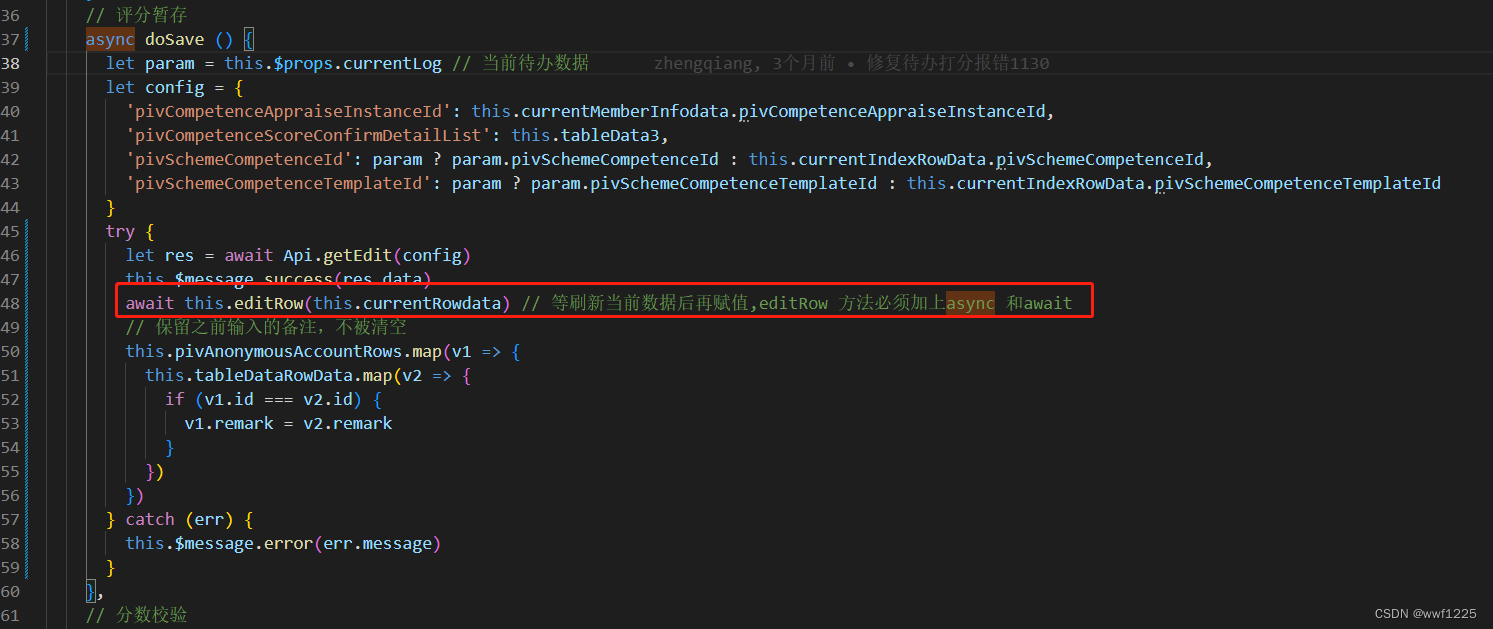
一,基本使用 其实就是之前学过的异步函数,异步编程在函数前写一个ansyc,就转化为异步函数,返回的是一个promise对象,于是就可以使用await关键字,可以把异步函数写成同步函数的形式,极大地提高代…...
如何从cpu改为gpu,pytorch,cuda
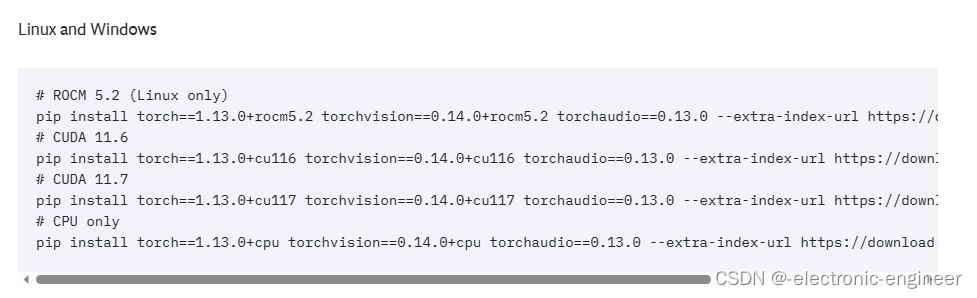
1.cmd输入nvcc -V 2.得到 cuda版本后,去pytorch官网 3.根据自己的cuda进行选择 4.复制上述链接,进入cmd 5.cmd中输入activate XXX,这里的"XXX"指代自己在工程中用到的环境 6.进入后,将刚才链接粘贴,回车等待下载结束 …...

JavaScript简介--语句--变量
目录 JavaScript简介 为什么学习 JavaScript JavaScript与ECMAScript的关系 JavaScript版本 JavaScript语句、标识符 语句 标识符 JavaScript保留关键字 变量 变量的命名规则 数据类型 变量的重新赋值 变量提升 运算符 条件语句 循环语句 JavaScript简介 JavaScri…...
Windows CMD 关闭,启动程序
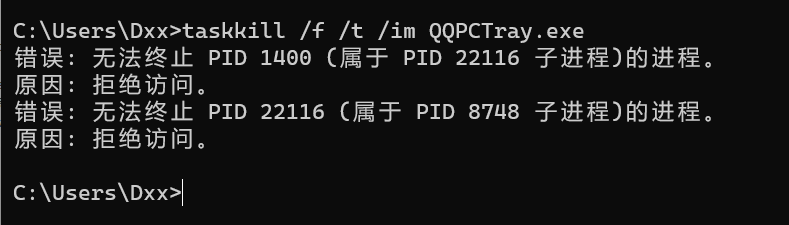
Windows CMD 关闭,启动程序 1. Windows 通过 CMD 命令行关闭程序 示例:通过 taskkill 命令关闭 QQ 管家,但是这里有个问题,使用命令行关闭 QQ 管家时,会提示“错误: 无法终止 PID 1400 (属于 PID 22116 子进程)的进程…...

统计XML标注文件中各标注类别的标签数量
目标检测任务重,担心数据集中各标签类别不均衡,想统计XML标注文件中各标注类别的标签数量,可以使用以下脚本: import os import glob import xml.etree.ElementTree as etdef count_labels(source_dir):file_list glob.glob(os.…...

一百六十、Kettle——Linux上安装的Kettle9.2.0连接Hive3.1.2
一、目标 Kettle9.2.0在Linux上安装好后,需要与Hive3.1.2数据库建立连接 之前已经在本地上用kettle9.2.0连上Hive3.1.2 二、各工具版本 (一)kettle9.2.0 kettle9.2.0安装包网盘链接 链接:https://pan.baidu.com/s/15Zq9w…...
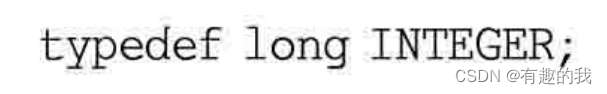
C++新经典03--共用体、枚举类型与typedef
共用体 共用体,也叫联合,有时候需要把几种不同类型的变量存放到同一段内存单元,例如,把一个整型变量、一个字符型变量、一个字符数组放在同一个地址开始的内存单元中。这三个变量在内存中占的字节数不同,但它们都从同…...

HCIP-OpenStack组件介绍
openstack把这些组件服务都集成到httpd服务中了,目的是为了提升性能。登入不了openstack在控制节点查下httpd服务,systemctl status httpd Horizon:提供webUI图形化界面的 Keystone:提供身份认证服务、授权、endpoint端点…...

2682. 找出转圈游戏输家
题目描述: n 个朋友在玩游戏。这些朋友坐成一个圈,按 顺时针方向 从 1 到 n 编号。从第 i 个朋友的位置开始顺时针移动 1 步会到达第 (i 1) 个朋友的位置(1 < i < n),而从第 n 个朋友的位置开始顺时针移动 1 步…...

RESTAPI简介与DRF使用
RESTAPI 以资源为url,通过不同的请求方式实现不同的行为。 以资源名作为url POST:增 …/student/ GET:查所有 …/student/ GET:查单个 …/student/<pk>/ 获取idpk的学生 DELETE:删 …/student/<pk>/ PUT&#…...
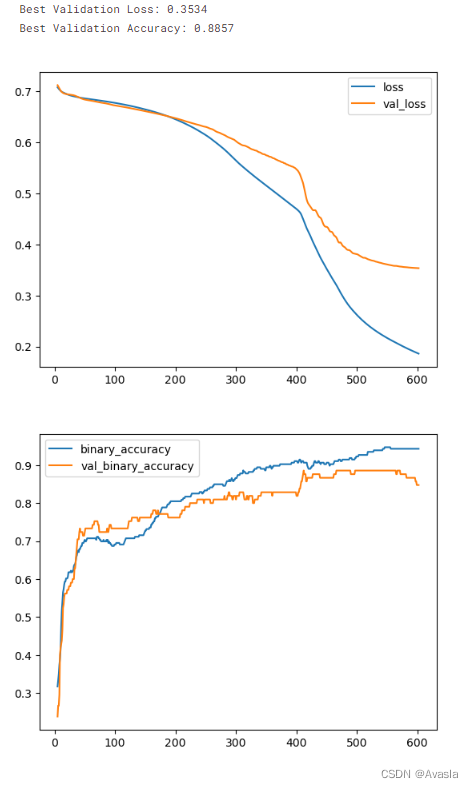
深度学习笔记(kaggle课程《Intro to Deep Learning》)
一、什么是深度学习? 深度学习是一种机器学习方法,通过构建和训练深层神经网络来处理和理解数据。它模仿人脑神经系统的工作方式,通过多层次的神经网络结构来学习和提取数据的特征。深度学习在图像识别、语音识别、自然语言处理等领域取得了…...

windows下载任意版本php
zzwindows.php.net - /downloads/releases/archives/ windows下载php,记录一下...

Linux命令
操作系统管理硬件设备,并为用户和应用程序提供一个简单的接口,以便于使用。(作为中间人,连接软件和硬件)不同应用领域的主流操作系统 桌面操作系统 Windows系列::用户群体大 macOS:适合于开发人…...

TDD(测试驱动开发)?
01、前言 很早之前,曾在网络上见到过 TDD 这 3 个大写的英文字母,它是 Test Driven Development 这三个单词的缩写,也就是“测试驱动开发”的意思——听起来很不错的一种理念。 其理念主要是确保两件事: 确保所有的需求都能被照…...

C/C++
const 作用 修饰变量,说明该变量不可以被改变;修饰指针,分为指向常量的指针(pointer to const)和自身是常量的指针(常量指针,const pointer);修饰引用,指向…...

CCF C³ 走进百度:大模型与可持续生态发展
2023年8月10日,由CCF CTO Club发起的第22期C活动在百度北京总部进行,以“AI大语言模型技术与生态发展”主题,50余位企业界、学界专家、研究人员就此进行深入探讨。 CCF C走进百度 本次活动,CCF秘书长唐卫清与百度集团副总裁、深…...

Vue使用html2canvas将DOM节点生成对应的PDF
要通过Vue使用html2canvas将DOM节点生成对应的PDF,您需要安装html2canvas和jspdf这两个库。html2canvas用于将DOM节点转换为Canvas,而jspdf用于将Canvas转换为PDF。以下是一个简单的示例代码,展示了如何使用html2canvas和jspdf生成PDF文件&am…...

专访阿里云席明贤,视频云如何运用大模型与小模型来破茧升级2.0
不久前,LiveVideoStack与阿里云视频云负责人席明贤(花名右贤)展开一场深度的对话,一个是圈内专业的社区媒体,一个是20年的IT老兵,双方有交集、有碰撞、有火花。 面对风云变幻的内外环境,阿里云…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
