堆 和 优先级队列(超详细讲解,就怕你学不会)
优先级队列
- 一、堆的概念特性
- 二、堆的创建
- 1、向下调整算法
- 2、向下调整建堆
- 3、向下调整建堆的时间复杂度
- 三、堆的插入
- 1、向上调整算法实现插入
- 2、插入创建堆的时间复杂度
- 三、堆的删除
- 四、Java集合中的优先级队列
- 1、PriorityQueue 接口概述及模拟实现
- 2、如何创建大根堆?
一、堆的概念特性
堆是具有以下性质的
完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆(大根堆);每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(小根堆)。
从堆的概念可知,堆是一棵完全二叉树,因此可以使用层序的规则采用顺序的方式来高效存储:

将元素存储到数组中后,可以根据二叉树的性质对树进行还原:
假设
i为节点在数组中的下标,则有:
- 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为
(i - 1)/2- 如果2 * i + 1小于节点个数(左孩子存在条件),则节点i的左孩子下标为
2 * i + 1,否则没有左孩子- 如果2 * i + 2 小于节点个数(右孩子存在条件),则节点i的右孩子下标为
2 * i + 2,否则没有右孩子
二、堆的创建
1、向下调整算法
示例:将集合{75,20,70,30,50,90,80,60,40}调整为小根堆
通过分析,已知集合的 “左右子树均满足小堆的性质” ,我们只需要将根节点向下调整到合适的位置,使集合整体为小堆即可。具体来说,我们可以细化为如下调整方法:
- 每次调整以
待调整结点、它的左右孩子结点构成的子树为单元进行“向下调整”- 每个单元以待调整结点为根节点,将左右孩子结点的最小值(小堆)和根节点进行比较,如果
根节点<min(左孩子,右孩子)调整结束,否则,待调整根节点和[min(左孩子,右孩子)]交换,交换完成后,继续重复这个步骤直到待调整结点为当前子树单元中的最小值,或待调整结点不在存在孩子结点,调整结束。

按照以上思路,下面是详细的代码实现:
/*** 小根堆->向下调整算法* @param parent 待调整结点* @param len 数组长度*/private void shiftDown(int[] array,int parent, int len) {int child = 2 * parent + 1;//根据完全二叉树性质,找到左孩子while (child < len) {//child<len判断孩子合法性//满足child<len至少存在左孩子if (child + 1 < len && array[child] > array[child + 1]) {//存在右孩子,且右孩子为左右孩子最小值child++;}//此时child一定是左右孩子的最小值的下标if (elem[child] < elem[parent]) {//满足条件,就交换int tmp = array[parent];array[parent] = array[child];array[child] = tmp;//交换完成后,继续以新的位置向下调整parent = child;child = 2 * parent + 1;} else {//array[parent] < array[child]调整结束break;}}}
小结:
- 在调整以
parent为根的二叉树时,必须要满足 parent 的左子树和右子树已经是堆了才可以向下调整。- 向下调整算法的最坏情况为从根一直比较到叶子,比较的次数为二叉树的高度,时间复杂度为
O(log₂N)。
2、向下调整建堆
在上面的探讨中,我们知道可以使用向下调整算法,将左右子树为堆的完全二叉树序列调整为堆,那么如果给出任意的完全二叉树序列(左右子树不满足堆的特性),我们又该如何调整为堆呢?
思路: 我们已知使用向下调整算法,
parent的左右子树必须满足堆的特性,对于任意普通完全二叉树序列,显然不能直接使用向下算法进行调整。不过我们知道一颗完全二叉树是由一颗颗左右子树构成的,虽然一颗普通的完全二叉树不能直接使用向下调整算法,但是倒数第一个非叶子结点构成的子树一定可以使用向下调整算法,所以如果我们可以先将下面的子树调整为堆,在继续对子树的根结点进行调整,这样根节点的左右子树就满足了堆的特性,可以直接使用向下调整算法。就这样一直向上对根结点进行向下调整,直到0下标对应的根节点调整完毕,整颗完全二叉树序列就满足了堆的特性了。
例如以序列{50,70,40,90,20,10,80,30,60}为例,调整后为{10,20,40,30,70,50,80,90,60}

具体实现:
/*** 向下调整建堆* @param array*/public void creatHeap(int[] array) {//清晰了思路之后,建堆就非常简单了//只需从最后一个非叶子结点开始,直到找到下标为0的根节点//每遇到一个结点向下调整,调用shiftDown即可for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {shiftDown(array,parent,array.length); }}
3、向下调整建堆的时间复杂度
假设序列为满叉树,假设树高为h,则最坏情况下第K层的2^(k-1)个结要向下移动h-k层。

三、堆的插入
1、向上调整算法实现插入
堆的插入相对来说较为简单,主要分为以下两步:
- 每次将新节点插入到堆的最后一个节点,因为底层维护的是一个一维数组,空间不够时要扩容。
- 将新插入的节点 向上调整,直到满足堆的性质。

所以说堆的插入并不难理解,核心就是对向上调整算法的实现:
- 每次调整以新节点构成的子树为单元,进行“向上调整”。
- 由于是在堆的基础上进行插入,所以每次调整只需将新节点和根节点进行比较,如果
根节点<新节点(小堆),调整结束,否则,根节点和新节点交换,交换完成后,继续重复这个步骤直到根节点<新节点,或,调整完下标为0的根节点,调整结束。
向上调整代码实现:
/*** 向上调整算法->小根堆* @param child 插入下标* elem 底层维护的一维数组*/private void shiftUp(int child) {int parent = (child-1)/2;根据完全二叉树性质,找双亲while (child >0) {//child>0判断孩子节点的合法性if (elem[child]<elem[parent]) {//满足条件,交换int tmp = elem[parent];elem[parent] = elem[child];elem[child] = tmp;//交换完成后,继续以新的位置向上调整child = parent;parent = (child-1)/2;} else {//elem[child]>elem[parent],调整结束break;}}}
堆的插入代码实现:
/*** 插入元素,也可以向上调整建堆* @param val* @return* elem 内部维护数组* usedSize 有效长度*/public boolean offerHeap(int val) {if (isFull()) {//扩容elem = Arrays.copyOf(elem,elem.length*2);}elem[usedSize++]=val;shiftUp(usedSize-1);return true;}public boolean isFull() {return usedSize==elem.length;}
小结:
- 堆的插入是在堆的基础上进行的插入。
- 向上调整算法的最坏情况为从叶子节点一直比较到根节点,比较的次数为二叉树的高度,时间复杂度为
O(log₂N)。
2、插入创建堆的时间复杂度
最坏情况下,假设堆为一颗满二叉树,的高度为h

三、堆的删除
规定:堆的删除一定删除的是堆顶元素
思路:由于堆的底层维护的是一个一维数组,所以每次删除,我们先将堆顶元素和堆的最后一个元素交换,然后让一维数组的size --,最后将交换后的堆顶元素 向下调整 即可。
- 判断堆是否为空,空堆不能删除
- 堆顶元素与堆尾元素交换
- 内部维护数组的有效数据减少 1
- 新的堆顶元素向下调整

代码实现:
/*** 删除堆顶元素*/public void pollHeap() {//判空if (isEmpty()) {return;}//交换int tmp = elem[usedSize-1];elem[usedSize-1] = elem[0];elem[0] = tmp;//删除+向下调整shiftDown(0,--usedSize);}public boolean isEmpty() {return usedSize == 0;}
四、Java集合中的优先级队列
1、PriorityQueue 接口概述及模拟实现
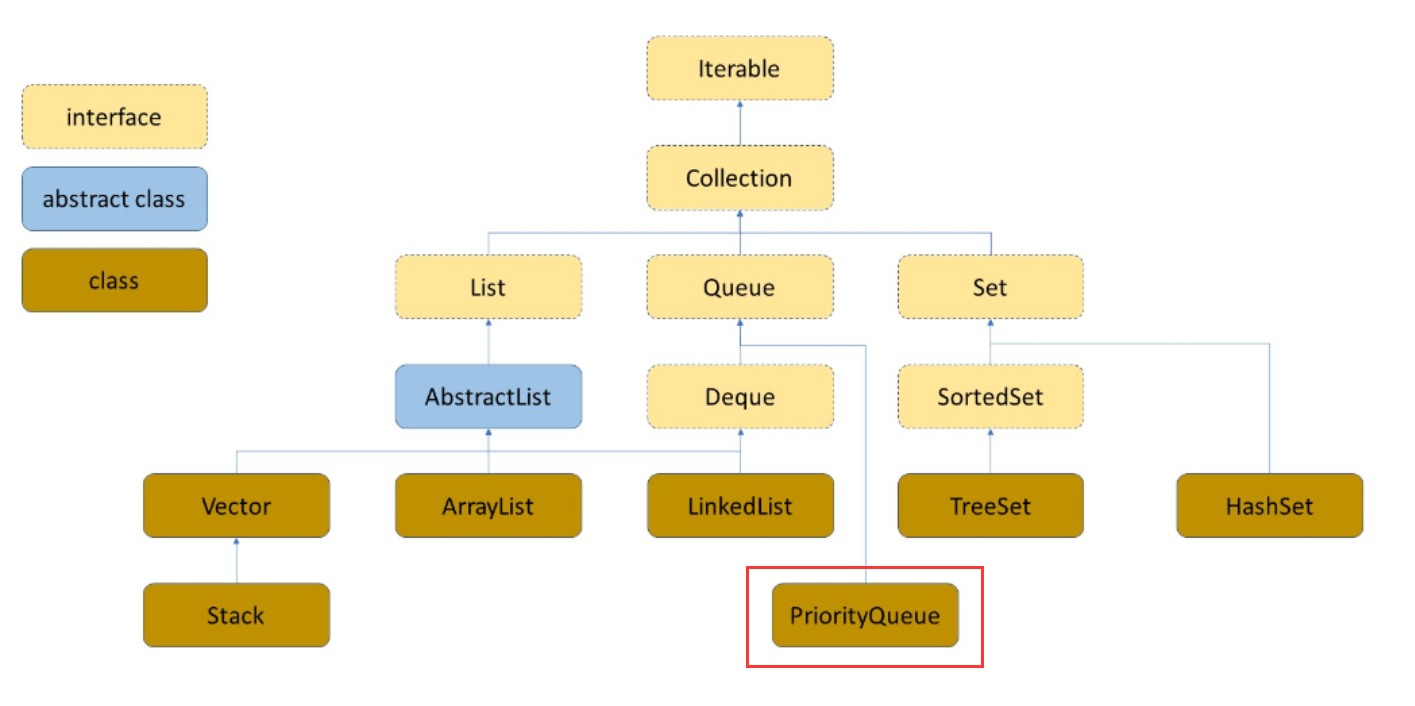
上面我们花那么多时间介绍堆,就是在为Java集合框架中的PriorityQueue做铺垫:
PriorityQueue,即优先级队列。优先级队列可以保证每次取出来的元素都是队列中的最小或最大的元素(Java优先级队列默认每次取出来的为最小元素)。JDK1.8中的PriorityQueue底层使用了堆这种数据结构。
PriorityQueue 注意事项:
- Java集合框架中提供了
PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的。- 使用时必须导入PriorityQueue所在的包
import java.util.PriorityQueue;- PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException异常
- 因为
null无法进行比较和排序,因此不能插入null对象,否则会抛出NullPointerException- 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
- 插入和删除元素的时间复杂度为
log₂N- PriorityQueue底层使用了堆数据结构,默认情况下是小堆,如果创建大堆,需要在构造方法中传入比较器。
常用的构造方法
| 构造器 | 功能介绍 |
|---|---|
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(intinitialCapacity) | 创建一个初始容量为initialCapacity的优先级队列,注意:initialCapacity不能小于1,否则会抛IllegalArgumentException异常 |
| PriorityQueue(Comparator c) | 传入比较器,构造大堆 |
常用的接口
| 函数名 | 功能介绍 |
|---|---|
| boolean offer(E e) | 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,空间不够时候会进行扩容 |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,返回null |
| E poll() | 移除优先级最高的元素并返回,如果优先级队列为空,返回null |
| int size() | 获取有效元素的个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,空返回true |
模拟实现PriorityQueue
由于 PriorityQueue 底层使用的是 堆 这种数据结构,所以PriorityQueue中的这些接口函数可以参考上面堆的操作,下面给出完整代码,大家自行理解:
public class PriorityQueue {public int[] elem;//数组public int usedSize;//有序长度public PriorityQueue(){elem = new int[11];}//1.判满public boolean isFull() {return usedSize==elem.length;}//2.判空public boolean isEmpty() {return usedSize == 0;}//3.插入元素public boolean offerHeap(int val) {if (isFull()) {//扩容elem = Arrays.copyOf(elem,elem.length*2);}elem[usedSize++]=val;shiftUp(usedSize-1);return true;}/*** 向上调整算法(小根堆)* @param child* elem 为底层维护的一维数组*/private void shiftUp(int child) {int parent = (child-1)/2;while (child >0) {if (elem[child]<elem[parent]) {int tmp = elem[parent];elem[parent] = elem[child];elem[child] = tmp;child = parent;parent = (child-1)/2;} else {break;}}}//4.删除堆顶元素public void pollHeap() {//判空if (isEmpty()) {return;}//交换int tmp = elem[usedSize-1];elem[usedSize-1] = elem[0];elem[0] = tmp;//删除+向下调整shiftDown(0,--usedSize);}/*** 向下调整算法(小根堆)* @param parent 待调整结点* @param len 数组长度*/private void shiftDown(int parent, int len) {//有左孩子int child = 2 * parent + 1;//这里是+1!!!while (child < len) {//有右孩子if (child + 1 < len && elem[child] > elem[child + 1]) {child++;}//此时childe一定是左右孩子的最小值的下标if (elem[child] < elem[parent]) {int tmp = elem[parent];elem[parent] = elem[child];elem[child] = tmp;parent = child;child = 2 * parent + 1;} else {break;}}}//5.清空public boolean isEmpty() {return usedSize == 0;}
}
2、如何创建大根堆?
我们已知默认情况下,PriorityQueue 是 小堆,如果创建大堆需要用户提供比较器,关于比较器我在 简介Object类+接口实例(深浅拷贝、对象数组排序)章节中已有过相关介绍,大家可点击连接自行参考,这里就不做过多冗余介绍了。
下面我演示一下创建大根堆常用的 3 3 3 中方式(以下这 3 种创建方式,本质上是没有区别的):
方式1: 直接创建比较类,实现 C o m p a r a t o r Comparator Comparator 接口,在构造方法中传入,比较类对象。
class Integercmp implements Comparator<Integer>{@Overridepublic int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}
public class Demo {public static void main1(String[] args) {Integercmp cmp = new Integercmp();Queue<Integer> maxHeap = new PriorityQueue<>(cmp);}
}
方式2: 使用匿名内部类
public class Demo {public static void main2(String[] args) {Queue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}});}
}
方式3: 使用 L a m b d a Lambda Lambda 表达式
public class Demo {public static void main3(String[] args) {Queue<Integer> maxHeap = new PriorityQueue<>((o1,o2)->{return o2.compareTo(o1);});}
}
相关文章:

堆 和 优先级队列(超详细讲解,就怕你学不会)
优先级队列 一、堆的概念特性二、堆的创建1、向下调整算法2、向下调整建堆3、向下调整建堆的时间复杂度 三、堆的插入1、向上调整算法实现插入2、插入创建堆的时间复杂度 三、堆的删除四、Java集合中的优先级队列1、PriorityQueue 接口概述及模拟实现2、如何创建大根堆…...

AIGC绘画:基于Stable Diffusion进行AI绘图
文章目录 AIGC深度学习模型绘画系统stable diffusion简介stable diffusion应用现状在线网站云端部署本地部署Stable Diffusion AIGC深度学习模型绘画系统 stable diffusion简介 Stable Diffusion是2022年发布的深度学习文本到图像生成模型,它主要用于根据文本的描述…...

python实现对Android系统手机亮度的调节
要实现对手机亮度的调节,需要使用Android系统的API。以下是一个简单的Python代码示例,演示如何使用ADB工具和Python脚本来控制Android设备的亮度: from adb.client import Client as AdbClient import os# 连接设备 client AdbClient(host&…...
《论文阅读14》FAST-LIO
一、论文 研究领域:激光雷达惯性测距框架论文:FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter IEEE Robotics and Automation Letters, 2021 香港大学火星实验室 论文链接论文github 二、论文概…...

Kotlin CompletableDeferred 入门
在 Kotlin 中,CompletableDeferred 是一个用于异步编程的类,它提供了一种实现异步操作和等待操作结果的方式。 CompletableDeferred 是 Deferred 接口的具体实现之一,可以用于表示一个可能会在将来完成的操作。它提供了以下主要功能…...

stm32g070的PD0/PD2 PA8和PB15
目前在用STM32G070做项目,其中PD2TIMER3去模拟PWM,PD0用作按键检测,测试发现PD0低电平检测没有问题,高电平检测不到,电路图如下图所示: 用万用表测试电平,高电平1.0V左右,首先怀疑硬…...
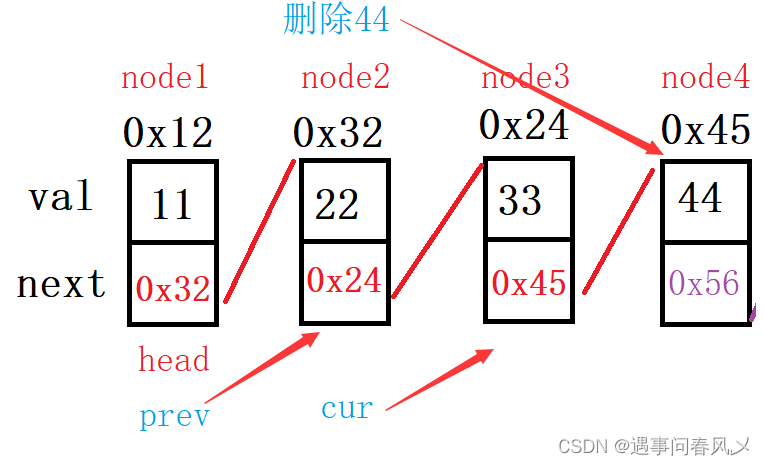
【数据结构】 链表简介与单链表的实现
文章目录 ArrayList的缺陷链表链表的概念及结构链表的分类单向或者双向带头或者不带头循环或者非循环 单链表的实现创建单链表遍历链表得到单链表的长度查找是否包含关键字头插法尾插法任意位置插入删除第一次出现关键字为key的节点删除所有值为key的节点回收链表 总结 ArrayLi…...
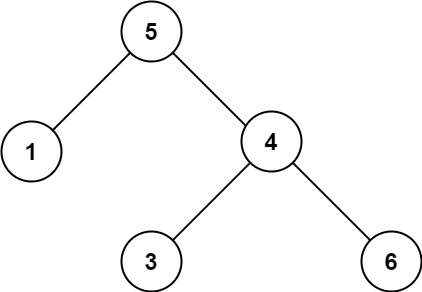
【Leetcode】98. 验证二叉搜索树
一、题目 1、题目描述 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。示例1: 输入:root = …...
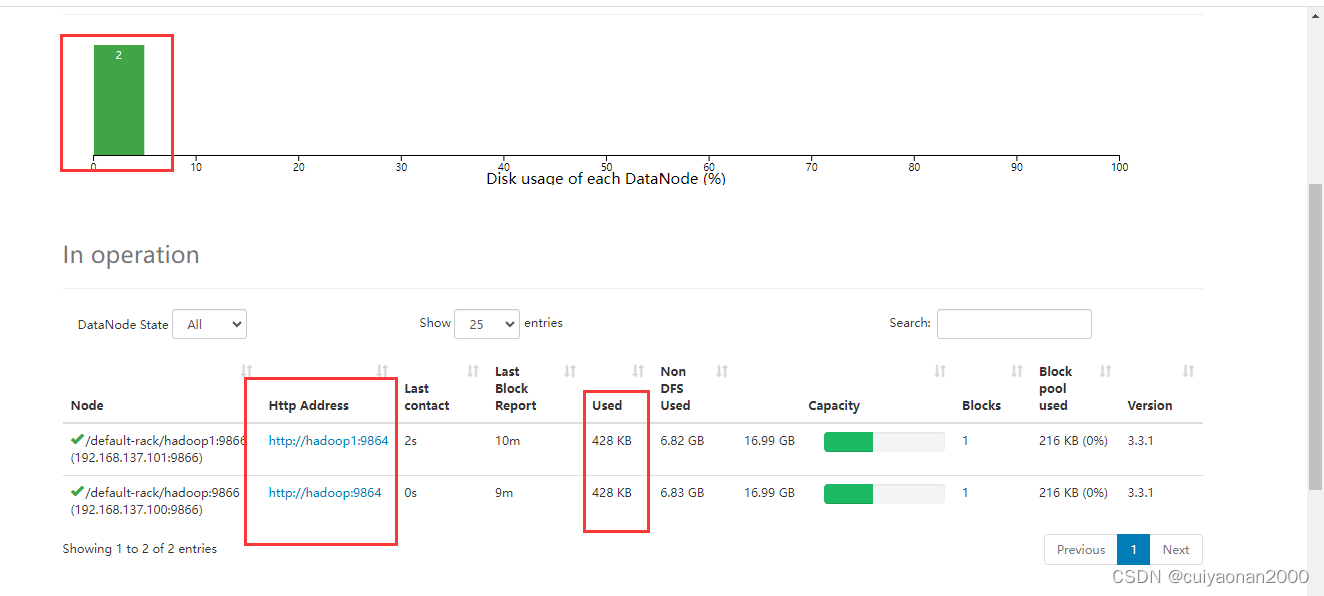
ViewFs And Federation On HDFS
序言 ViewFs 是在Federation的基础上提出的,用于通过一个HDFS路径来访问多个NameSpace,同时与ViewFs搭配的技术是client-side mount table(这个就是具体的规则配置信息可以放置在core.xml中,也可以放置在mountTable.xml中). 总的来说ViewFs的其实就是一个中间层,用于去连接不…...

每日一学——无线基础知识
无线局域网(Wireless Local Area Network,简称 WLAN)是一种使用无线通信技术连接多个无线终端设备的局域网。它通常基于无线电波传输数据,并使用无线接入点(Access Point,简称 AP)来连接无线设备…...
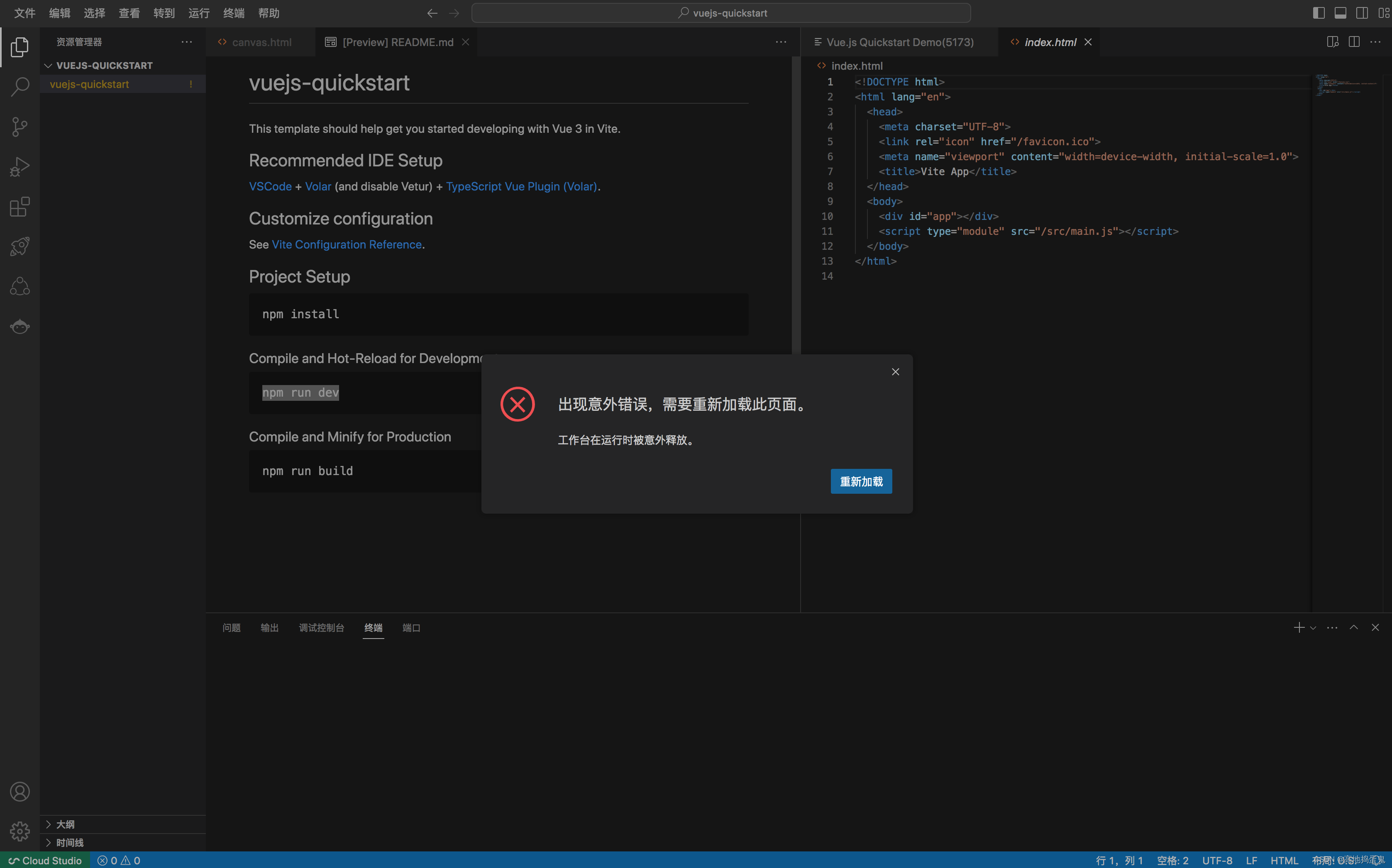
【腾讯云 Cloud Studio 实战训练营】在线 IDE 编写 canvas 转换黑白风格头像
关于 Cloud Studio Cloud Studio 是基于浏览器的集成式开发环境(IDE),为开发者提供了一个永不间断的云端工作站。用户在使用Cloud Studio 时无需安装,随时随地打开浏览器就能在线编程。 Cloud Studio 作为在线IDE,包含代码高亮、自动补全、Gi…...
【Hystrix技术指南】(7)故障切换的运作流程原理分析(含源码)
背景介绍 目前对于一些非核心操作,如增减库存后保存操作日志发送异步消息时(具体业务流程),一旦出现MQ服务异常时,会导致接口响应超时,因此可以考虑对非核心操作引入服务降级、服务隔离。 Hystrix说明 官方…...

Springboot 整合MQ实现延时队列入门
延时队列 添加依赖配置文件队列TTL代码架构图交换机、队列、绑定配置文件代码生产者代码消费者代码延时队列优化添加普通队列配置代码生产者发送消息是进行设置消息的ttl 通过MQ 插件实现延时队列代码架构图配置交换机生产者代码消费者代码测试发送 添加依赖 <!-- rabbitMQ …...
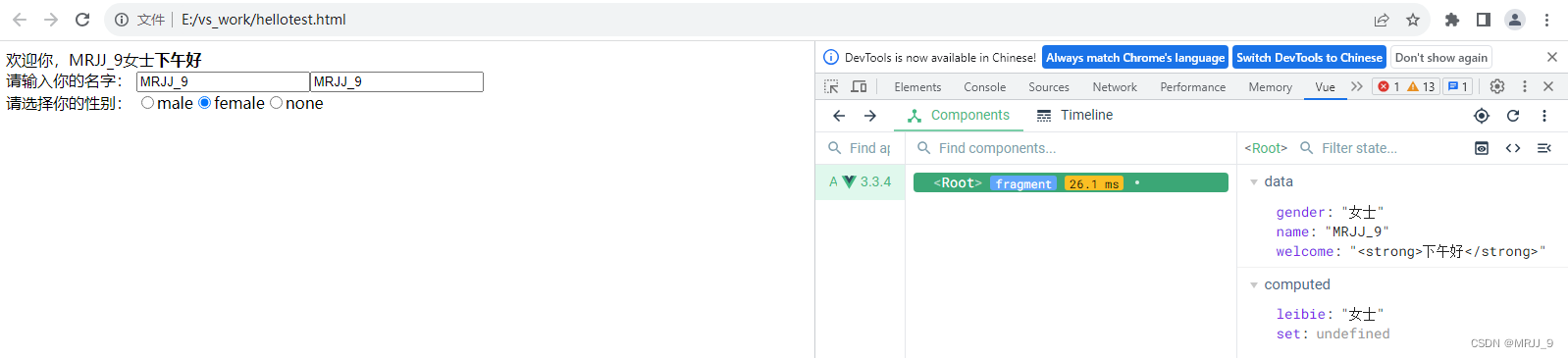
前端基础(Vue框架)
前言:前端开发框架——Vue框架学习。 准备工作:添加Vue devtools扩展工具 具体可查看下面的这篇博客 添加vue devtools扩展工具添加后F12不显示Vue图标_MRJJ_9的博客-CSDN博客 Vue官方学习文档 Vue.js - 渐进式 JavaScript 框架 | Vue.js 目录 MV…...
【实用插件】ArcGIS for AutoCAD插件分享下载
ArcGIS包含一系列功能,其中ArcGIS for AutoCAD一个免费的可下载的AutoCAD插件,它可简化将CAD和GIS数据整合在一起的过程提供互操作性。 ArcGIS for AutoCAD互操作性平台将连接AutoCAD和 ArcGIS,以增强使用地理环境设计CAD工程图时的用户体验…...
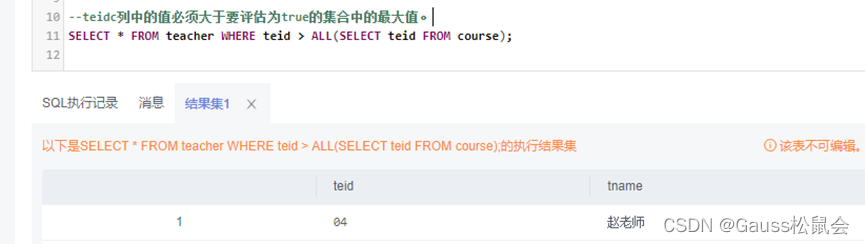
GaussDB数据库SQL系列-子查询
目录 一、前言 二、GaussDB SQL子查询表达式 1、EXISTS/NOT EXISTS 2、IN/NOT IN 3、ANY/SOME 4、ALL 三、GaussDB SQL子查询实验示例 1、创建实验表 2、EXISTS/NOT EXISTS示例 3、IN/NOT IN 示例 4、ANY/SOME 示例 5、ALL示例 四、注意事项及建议 五、小结 一、…...
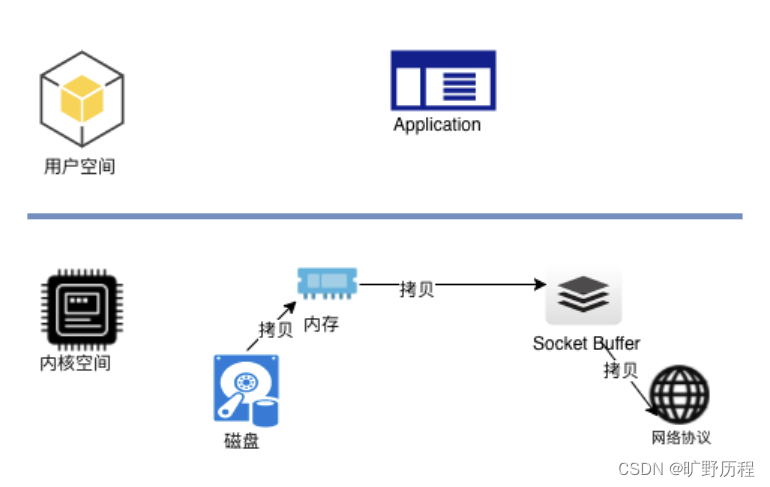
Kafka 什么速度那么快
批量发送消息 Kafka 采用了批量发送消息的方式,通过将多条消息按照分区进行分组,然后每次发送一个消息集合,看似很平常的一个手段,其实它大大提升了 Kafka 的吞吐量。 消息压缩 消息压缩的目的是为了进一步减少网络传输带宽。而…...
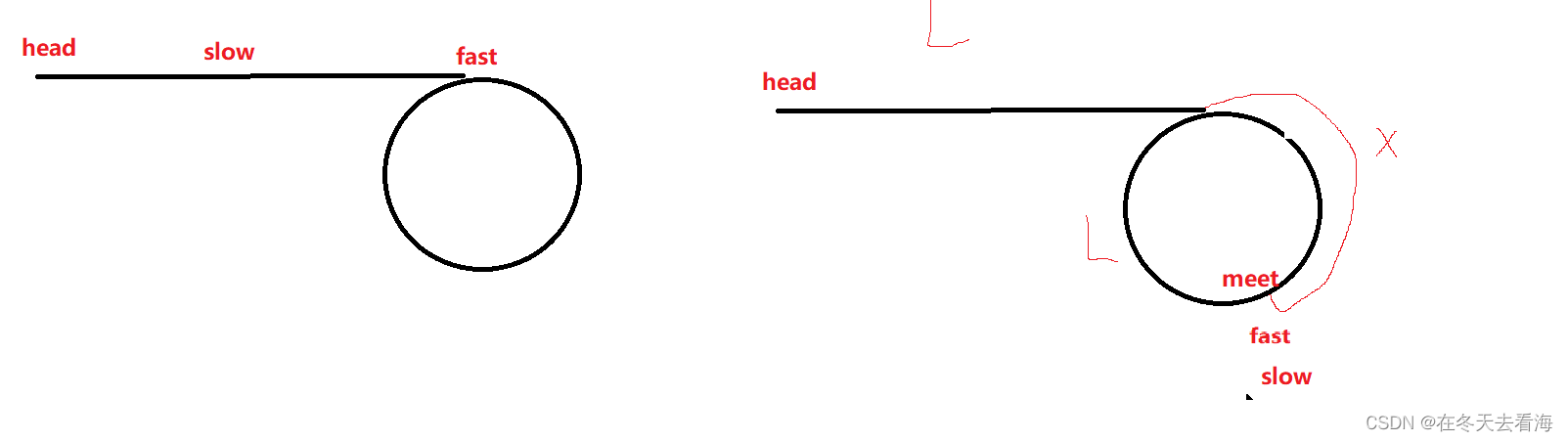
环形链表笔记(自用)
环形链表 不管怎么样slow最多走半圈了, 快慢指针slow走一步,fast走两步最合适,因为假设fast和slow相差n每一次他们前进,就会相差n-1步,这样他们一定会相遇,如果是环形链表的话。 代码 /*** Definition for…...

js循环中发起请求数据不一致问题
项目场景: 在公司的一个项目中需要使用循环更改查询条件,然后查询子表数据,但是在查询过程中for下面的key变化了之后,查询中的key却并没有变化,导致查询的参数不一致,从未结果数据出错 for(let i 0;i<…...
工作流自动化:提升效率、节约成本的重要工具
在现代社会中,软件和技术的运用使得我们的日常活动变得更加简单和高效。然而,这些技术也有自身的特点和独特之处。尽管我们使用这些工具来简化工作,但有时仍需要一些人工干预,比如手动数据录入。在工作场所中,手动数据…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
