当前位置： 首页 > news >正文

Spark操作Hive表幂等性探索

news 2026/2/9 2:40:08

前言

旁边的实习生一边敲着键盘一边很不开心的说：做数据开发真麻烦，数据bug排查太繁琐了，我今天数据跑的有问题，等我处理完问题重新跑了代码，发现报表的数据很多重复，准备全部删了重新跑。

我：你的数据操作具备幂等性吗？

实习生：啥是幂等性？数仓中的表还要考虑幂等性吗？

幂等性

数据幂等性是指在多次执行相同操作时，最终的结果与执行一次操作的结果相同。具体来说，无论重复执行多少次相同的操作，操作的结果应该保持一致。

在数据处理和数据操作中，保持数据幂等性非常重要。如果操作不具备幂等性，可能会导致数据的重复、丢失或不一致。例如，向数据库中插入数据的操作如果没有幂等性，则在多次执行操作时可能会导致重复插入相同的数据。

幂等性对于保证数据一致性和可靠性非常重要，特别是在分布式系统或并发环境下。在这些环境中，多个相同操作可能同时或近乎同时执行，因此操作的幂等性能够保证数据的正确性。

在数据处理流程中，可以使用一些技术或设计策略来实现数据的幂等性，例如使用唯一标识符来避免重复处理，使用幂等操作来保证数据操作的一致性，或者使用事务来保证操作的原子性和幂等性等。

实习生看到这说：我们大数据用的是Hive表，不是那种关系型数据库的表。关系型数据表我可以在每次操作之前，根据某些条件（比如时间区间等）删除掉对应的数据，可是我用Spark开发完，要写入Hive表，这怎么实现幂等性？
我：你应该静下心来学习Spark基础了。<

相关文章：

Spark操作Hive表幂等性探索

前言 旁边的实习生一边敲着键盘一边很不开心的说：做数据开发真麻烦，数据bug排查太繁琐了，我今天数据跑的有问题，等我处理完问题重新跑了代码，发现报表的数据很多重复，准备全部删了重新跑。 我：你的数据操作具备幂等性吗？ 实习生：啥是幂等性？数仓中的表还要考虑幂等…...

编程日记 2023/8/19 3:41:19

【可变形卷积3】 DCNv2 安装

使用RTM3D 代码&#xff0c;CenterTrack代码需要用DCN 1、安装DCNv2 &#xff08;1&#xff09;github上最新版的DCNv2源码在"https://github.com/CharlesShang/DCNv2"&#xff0c;但是该版本源码不支持PyTorch1.7&#xff0c;如果使其支持PyTorch1.7需要做以下修改…...

编程日记 2023/8/19 3:40:18

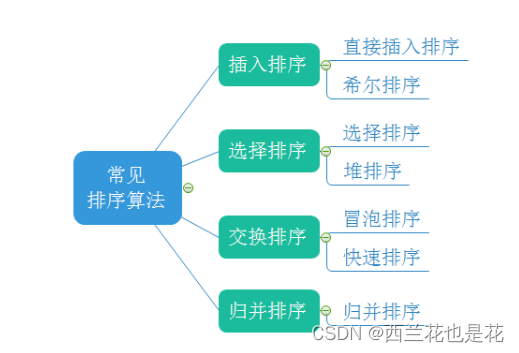
归并排序 与 计数排序

目录 1.归并排序 1.1 递归实现归并排序&#xff1a; 1.2 非递归实现归并排序 1.3 归并排序的特性总结: 1.4 外部排序 2.计数排序 2.1 操作步骤: 2.2 计数排序的特性总结: 3. 7种常见比较排序比较 1.归并排序 基本思想: 归并排序(MERGE-SORT)是建立在归并操作上的一种…...

编程日记 2023/8/19 3:39:12

机器学习之逻辑回归

import numpy as np import pandas as pd from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LogisticRegression # 获得数据 names[Sample code number,Clump Thickness,Uniformity…...

编程日记 2023/8/19 3:38:10

操作符详解上（非常详细）

目录 二进制介绍二进制2进制转10进制10进制转2进制数字2进制转8进制和16进制2进制转8进制2进制转16进制 原码、反码、补码移位操作符左移操作符右移操作符 位操作符&#xff1a;&、|、^逗号表达式 二进制介绍 在初学计算机时我们常常会听到2进制、8进制、10进制、16进制……...

编程日记 2023/8/19 3:37:08

React 高阶组件(HOC)

React 高阶组件(HOC) 高阶组件不是 React API 的一部分&#xff0c;而是一种用来复用组件逻辑而衍生出来的一种技术。 什么是高阶组件 高阶组件就是一个函数&#xff0c;且该函数接受一个组件作为参数&#xff0c;并返回一个新的组件。基本上&#xff0c;这是从 React 的组成…...

编程日记 2023/8/19 3:36:07

【NepCTF2023】复现

文章目录 【NepCTF2023】复现MISC与AI共舞的哈夫曼codesc语言获取环境变量 小叮弹钢琴陌生的语言你也喜欢三月七么Ez_BASIC_IImisc参考 WEBez_java_checkinPost Crad For You独步天下配置环境独步天下-镜花水月环境变量提权 独步天下-破除虚妄总结 独步天下-破除试炼_加冕成王知…...

编程日记 2023/8/19 3:35:05

大文件切片上传

创建组件&#xff1a;创建一个组件用于处理文件上传&#xff0c;命名为Upload.vue。 <template><div><input type"file" change"handleFileChange" /><button click"startUpload">开始上传</button></div> …...

编程日记 2023/8/19 3:34:04

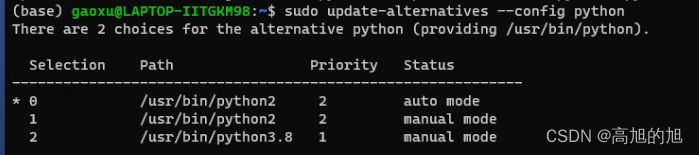
ubuntu切换python版本

在没有安装类似anoconda的管理工具的时候&#xff0c;我们常常会被Ubuntu下的Python版本切换问题所头疼。 可以使用update-alternatives工具进行python版本的任意切换 当使用update-alternatives工具来切换Ubuntu系统上的Python版本时&#xff0c;您实际上是在系统范围内选择…...

编程日记 2023/8/19 3:33:01

docker 安装 elasticsearch、kibana 7.4.2

切换root 用户 su root 拉起镜像 docker pull elasticsearch:7.4.2 docker pull kibana:7.4.2 #1、创建Elasticsearch配置文件夹 mkdir -p /mydata/elasticsearch/config ​ #2、创建Elasticsearch数据文件夹 mkdir -p /mydata/elasticsearch/data #3、创建Elasticsearch插件…...

编程日记 2023/8/19 3:32:00

【es6】函数参数设置默认值

1、es6之前的函数参数默认值写法 1.1、使用短路或||的写法 当y为空时&#xff0c;y判断为false &#xff0c;走||右边的&#xff0c;所以y world;当y不为空时&#xff0c;y判断为true&#xff0c;不需要再运行||右边的&#xff0c;所以 y y function log(x, y) {y y || W…...

编程日记 2023/8/19 3:30:57

Pytest和Unittest测试框架的区别？

如何区分这两者&#xff0c;很简单unittest作为官方的测试框架&#xff0c;在测试方面更加基础&#xff0c;并且可以再次基础上进行二次开发&#xff0c;同时在用法上格式会更加复杂&#xff1b;而pytest框架作为第三方框架&#xff0c;方便的地方就在于使用更加灵活&#xff0…...

编程日记 2023/8/19 3:29:56

C#基础知识（一）

一、C#程序结构 《1》命名空间的声明&#xff08;namespace declaration&#xff09; 《2》一个class 《3》class方法 《4》class属性 《5》一个main方法 《6》语句&#xff08;statements&#xff09;&表达式&#xff08;Expressions&#xff09; 《7》注释 注&#xff1a…...

编程日记 2023/8/19 3:28:54

我还不知道？Android组件化插件化模块化

Android组件化、插件化和模块化是针对Android应用程序开发的一种架构设计思想和开发方式。 组件化&#xff08;Componentization&#xff09;&#xff1a; 组件化是将一个大型的Android应用程序拆分成多个独立的组件&#xff08;Module&#xff09;&#xff0c;每个组件可以独…...

编程日记 2023/8/19 3:27:52

借助 AI 工具，真的能成为 10x 工程师？

或许你听说过 10x 工程师吗&#xff1f; 如果你问猎头公司 10x 工程师是什么意思&#xff0c;他们可能会说 “生产力”&#xff01;10x 是指完成任务比别人快 10 倍的工程师。 2019 年&#xff0c;Twitter 上就曾经对 10 x 工程师这一议题有过一次空前热烈的讨论&#xff0c;引…...

编程日记 2023/8/19 3:26:51

TypeScript 面向对象

TypeScript 接口 TypeScript 接口定义如下&#xff1a; interface interface_name { } 以下实例中&#xff0c;我们定义了一个接口 IPerson&#xff0c;接着定义了一个变量 customer&#xff0c;它的类型是 IPerson。 customer 实现了接口 IPerson 的属性和方法。 interf…...

编程日记 2023/8/19 3:25:48

k8s 中快速启动curl pod 做api test

场景 k8s上运行的pod需要进行api测试,由于开发使用的镜像都是最小化构建,不能保证现有的pod中一定有curl工具,于是需要启动一个带有curl工具的测试pod专门进行api测试 指令 kubectl run curl-test-pod --imagecurlimages/curl -n {namespace} -i --tty -- sh上述指令实现在指…...

编程日记 2023/8/19 3:24:47

神经网络基础-神经网络补充概念-56-迁移学习

迁移学习&#xff08;Transfer Learning&#xff09;是一种机器学习技术&#xff0c;旨在将在一个任务上学到的知识或模型迁移到另一个相关任务上&#xff0c;以提高新任务的性能。迁移学习的核心思想是通过利用源领域&#xff08;source domain&#xff09;的知识来改善目标领…...

编程日记 2023/8/19 3:23:45

力扣：65. 有效数字（Python3）

题目&#xff1a; 有效数字&#xff08;按顺序&#xff09;可以分成以下几个部分&#xff1a; 一个 小数 或者 整数&#xff08;可选&#xff09;一个 e 或 E &#xff0c;后面跟着一个 整数 小数&#xff08;按顺序&#xff09;可以分成以下几个部分&#xff1a; &#xff08;…...

编程日记 2023/8/19 3:22:44

003-Spring boot 启动流程分析

目录 启动流程分析创建 SpringApplication启动 run(String... args) 读取配置流程分析listeners.environmentPrepared解析配置文件详细分析EnvironmentPostProcessor 详细分析 启动流程分析 SpringApplication.run(App.class, args);return new SpringApplication(primarySour…...

编程日记 2023/8/19 3:21:42

挑战杯推荐项目

“人工智能”创意赛 - 智能艺术创作助手&#xff1a;借助大模型技术&#xff0c;开发能根据用户输入的主题、风格等要求&#xff0c;生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用&#xff0c;帮助艺术家和创意爱好者激发创意、提高创作效率。 ​ - 个性化梦境…...

编程新知 2025/11/6 5:46:16

大数据学习栈记——Neo4j的安装与使用

本文介绍图数据库Neofj的安装与使用&#xff0c;操作系统&#xff1a;Ubuntu24.04&#xff0c;Neofj版本&#xff1a;2025.04.0。 Apt安装 Neofj可以进行官网安装&#xff1a;Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

编程新知 2026/2/8 4:37:08

蓝牙 BLE 扫描面试题大全(2)：进阶面试题与实战演练

前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1)&#xff1a;从基础到实战的深度解析-CSDN博客&#xff0c;但实际面试中&#xff0c;企业更关注候选人对复杂场景的应对能力&#xff08;如多设备并发扫描、低功耗与高发现率的平衡&#xff09;和前沿技术的…...

编程新知 2026/2/5 3:41:42

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序

一、开发准备 ​​环境搭建​​&#xff1a; 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 ​​项目创建​​&#xff1a; File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

编程新知 2025/9/5 12:16:40

生成 Git SSH 证书

&#x1f511; 1. ​​生成 SSH 密钥对​​ 在终端&#xff08;Windows 使用 Git Bash&#xff0c;Mac/Linux 使用 Terminal&#xff09;执行命令&#xff1a; ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" ​​参数说明​​&#xff1a; -t rsa&#x…...

编程新知 2025/9/18 11:31:13

【算法训练营Day07】字符串part1

文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接&#xff1a;344. 反转字符串 双指针法&#xff0c;两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

编程新知 2025/8/27 14:38:58

Python爬虫（二）：爬虫完整流程

爬虫完整流程详解&#xff08;7大核心步骤实战技巧&#xff09; 一、爬虫完整工作流程 以下是爬虫开发的完整流程&#xff0c;我将结合具体技术点和实战经验展开说明&#xff1a; 1. 目标分析与前期准备 网站技术分析&#xff1a; 使用浏览器开发者工具&#xff08;F12&…...

编程新知 2025/10/19 5:48:51

Module Federation 和 Native Federation 的比较

前言 Module Federation 是 Webpack 5 引入的微前端架构方案&#xff0c;允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

编程新知 2026/1/31 13:48:37

k8s业务程序联调工具-KtConnect

概述 原理 工具作用是建立了一个从本地到集群的单向VPN&#xff0c;根据VPN原理&#xff0c;打通两个内网必然需要借助一个公共中继节点&#xff0c;ktconnect工具巧妙的利用k8s原生的portforward能力&#xff0c;简化了建立连接的过程&#xff0c;apiserver间接起到了中继节…...

编程新知 2026/2/1 4:14:14

UR 协作机器人「三剑客」：精密轻量担当（UR7e）、全能协作主力（UR12e）、重型任务专家（UR15）

UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中&#xff0c;UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化&#xf…...

编程新知 2026/2/2 2:47:37