耕地单目标语义分割实践——Pytorch网络过程实现理解
一、卷积操作
(一)普通卷积(Convolution)


(二)空洞卷积(Atrous Convolution)
根据空洞卷积的定义,显然可以意识到空洞卷积可以提取到同一输入的不同尺度下的特征图,具有构建特征金字塔的基础。

(三)深度可分离卷积(Depthwise-Separable Convolution)
在对深度可分离卷积具有一定的了解后,我产生了一种“既然模型参数大幅度减少了,那么该模型的运行时间应该也会大幅度缩减”的想法。可是,当我分别在GPU、CPU上进行实验时,我发现结果并不与我当初所想相同。后经过查阅资料[13][14]进一步加深了我对硬件计算优势以及深度可分离卷积的理解。(注:1)实际上,通常我们一层卷积之后都会加深特征图深度,但是我所设计的实验保持了原有深度前向计算。同时,一个卷积网络也应顾及到模型精确性适当使用DSC而非完全;2)参考资料[13]具有与我相同思想的不同模型之间的对比试验)
适合GPU运算的运算类型有1)大量轻量级运算;2)高度并行运算:3)计算密集型:4)浮点型运算等。CPU擅长于串行运行。

针对DSC有可能出现模型参数大幅度减少,但模型运行时间却不下降的现象,可能存在以下原因:
1)许多深度学习加速器和库(如CUDA和cuDNN),对深度可分离卷积的优化可能不够;
2)尽管深度可分离卷积需要的乘、加运算较少,但与普通卷积相比,它可能需要更多的内存访问操作,这在GPU上可能导致效率降低;
3)受限于自身设备的显存容量。

(四)转置卷积(Transpose Convolution)
转置卷积是一种卷积,它将输入和核进行了重新排列,同卷积一般是做下采样不同,它通常用作上采样。如果卷积将输入从(h,w)变成了(h‘,w'),同样超参数下转置卷积将(h‘,w')变成(h,w)。
转置卷积可以变为对应核的矩阵乘法。转置卷积是一种变化了输入和核的卷积,来得到上采样的目的,其并不等同于数学上的反卷积概念。在深度学习中,反卷积神经网络指用了转置卷积的神经网络。
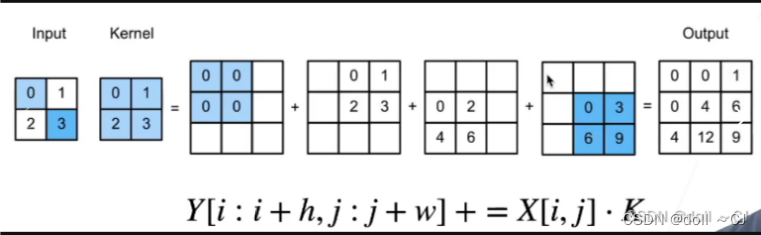
二、池化操作
池化操作主要的作用为1)减少网络计算量与内存消耗;2)增加感受野大小;3)增加平移不变性(即较小的特征偏移也不影响特征输出)。从某种角度上来说,Pooling操作是一种对现存硬件计算能力和存储设备的妥协,其在某些卷积神经网络(如Resnet)可以被忽略。

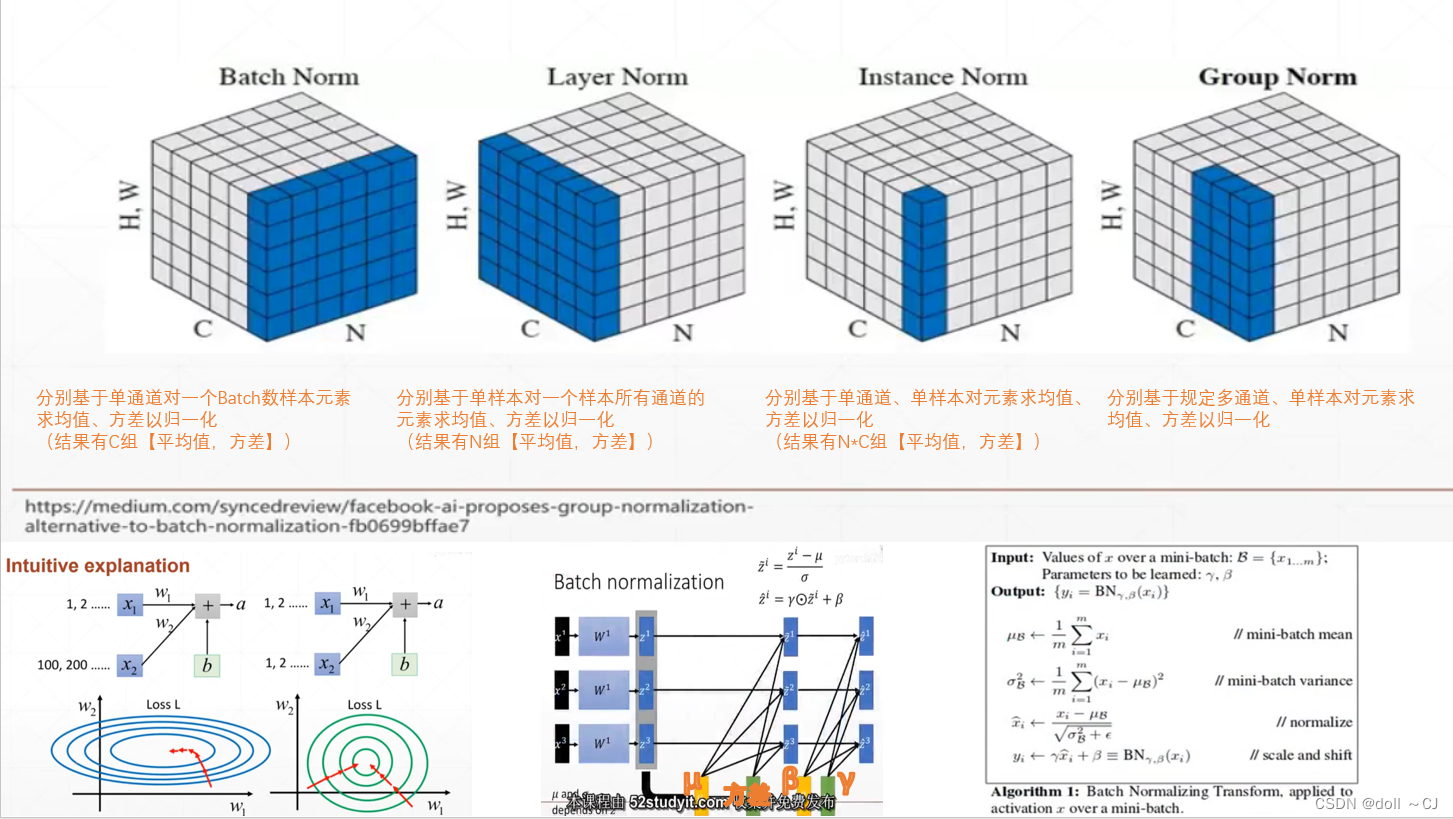
三、数据归一化操作
数据归一化操作中(以BatchNormal为例),β和γ参数是需要计算梯度更新的学习参数,数据归一化行为在Train、Test过程中是不一样的。在Train过程中,我们需要不断计算反向梯度更新β、γ参数,而在Test过程中我们是会固定前面学习得到的β、γ参数(Pytorch中测试调用net.eval())。
批量归一化的主要作用:
1)控制传入下一层的特征图数据,有效减少梯度爆炸和梯度消失的可能;
2)减少对参数初始化的依赖;
3)便于应用更高的学习率,实现更快的收敛。
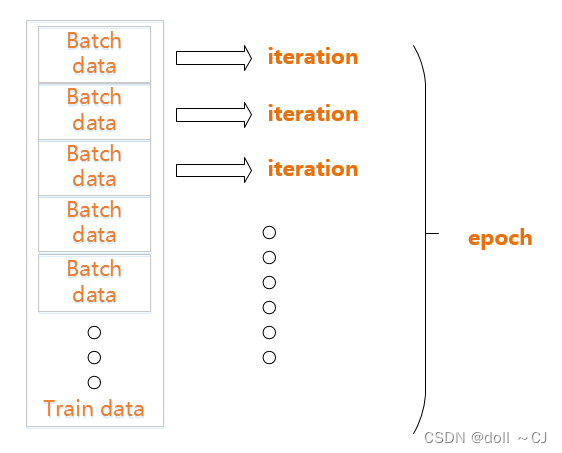
四、深度学习中的Batch、Epoch
反向梯度计算以更新模型权值等参数发生于一个Batch迭代后。初期训练时,我认为足够的Batch样本数对于模型的快速收敛较为重要。那么,如果受限于自身GPU显存限制,我们可以进一步权衡在CPU上训练更多样本数的Batch,而放宽训练时间这一要求。
在合理范围内,增大Batch_Size具有以下优点[11]:
1)内存利用率提高了,大矩阵乘法的并行化效率提高;
2)跑完一次epoch(全数据集)所需的迭代次数减少,对于相同数据量的处理速度进一步加快;
3)在一定范围内,一般来说Batch Size越大,其确定的下降方向越可能对准极值低点,训练引起损失震荡越小。
五、在.ipynb文件中调用不同路径位置文件的方法
(1)首先被引.ipynb文件转换为.py文件,然后在.ipynb文件中头部添加sys.path.insert(0,r"绝对路径")或sys.path.append(r“绝对路径”)[17]。
(2)编写.ipynb解析文件置于同一文件夹下[16]。
Pytorch参考资料:
[1] 在CV/NLP/DL领域中,有哪些修改一行代码或者几行代码提升性能的算法? - 圈圈的回答 - 知乎
https://www.zhihu.com/question/427088601/answer/1544199551.
[2]在CV/NLP/DL领域中,有哪些修改一行代码或者几行代码提升性能的算法? - 陀飞轮的回答 - 知乎 https://www.zhihu.com/question/427088601/answer/1587333057
[3]PyTorch 中文文档
[4]课时61 什么是卷积-1_哔哩哔哩_bilibili
[5]PyTorch Forums
[6]https://en.wikipedia.org/wiki/Convolutional_neural_network
[7]数字图像处理:第四版/(美)拉斐尔C.冈萨雷斯(Rafael C.Gonzalez),(美)理查德E.伍兹(Richard E.Woods)著;阮秋琦等译.——北京:电子工业出版社,2020.5.
[8]深入理解空洞卷积 - 知乎
[9]演示分组,深度,深度可分离卷积|3D卷积神经网络_哔哩哔哩_bilibili
[10]卷积神经网络之深度可分离卷积(Depthwise Separable Convolution) - 知乎
[11]谈谈深度学习中的 Batch_Size_机器学习batch size作用_ycheng_sjtu的博客-CSDN博客
[12]pytorch统计模型参数量并输出_pytorch输出模型参数量_xidaoliang123的博客-CSDN博客
[13]薰风读论文:MobileNet 详解深度可分离卷积,它真的又好又快吗? - 知乎
[14]三分钟搞懂CPU, GPU, FPGA计算能力 - 知乎
Python参考资料:
[15]Python:为什么类中的私有属性可以在外部赋值并访问_python 类外访问私有属性_Ding Jiaxiong的博客-CSDN博客
[16]调用jupyter notebook文件内的函数一种简单方法_AlexInML的博客-CSDN博客
[17]Jupyter Notebook引入外部的py文件中的方法_dirtyboy6666的博客-CSDN博客
相关文章:

耕地单目标语义分割实践——Pytorch网络过程实现理解
一、卷积操作 (一)普通卷积(Convolution) (二)空洞卷积(Atrous Convolution) 根据空洞卷积的定义,显然可以意识到空洞卷积可以提取到同一输入的不同尺度下的特征图&…...

画质提升+带宽优化,小红书音视频团队端云结合超分落地实践
随着视频业务和短视频播放规模不断增长,小红书一直致力于研究:如何在保证提升用户体验质量的同时降低视频带宽成本? 在近日结束的音视频技术大会「LiveVideoStackCon 2023」上海站中,小红书音视频架构视频图像处理算法负责人剑寒向…...
【傅里叶级数与傅里叶变换】数学推导——3、[Part4:傅里叶级数的复数形式] + [Part5:从傅里叶级数推导傅里叶变换] + 总结
文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。 文章全部链接: 基础知识点 Part1:三角函数系的正交性 Part2:T2π的周期函数的傅里叶级数展开 P…...

第二章MyBatis入门程序
入门程序 创建maven程序 导入MyBatis依赖。pom.xml下导入如下依赖 <dependencies><dependency><groupId>org.mybatis</groupId><artifactId>mybatis</artifactId><version>3.5.6</version></dependency><dependen…...

AgentBench::AI智能体发展的潜在问题(二)
从历史上看,几乎每一种新技术的广泛应用都会在带来新机遇的同时引发很多新问题,AI智能体也不例外。从目前的发展看,AI智能体的发展可能带来的新问题可能包括如下方面: 第二是AI智能体的普及将有可能进一步加剧AI造成的技术性失业。…...
:逻辑运算符(上))
C++中的运算符总结(4):逻辑运算符(上)
C中的运算符总结(4):逻辑运算符(上) 8、逻辑运算 NOT、 AND、 OR 和 XOR 逻辑 NOT 运算用运算符!表示,用于单个操作数。表 1是逻辑 NOT 运算的真值表,这种运算将提供的布尔标记反转࿱…...
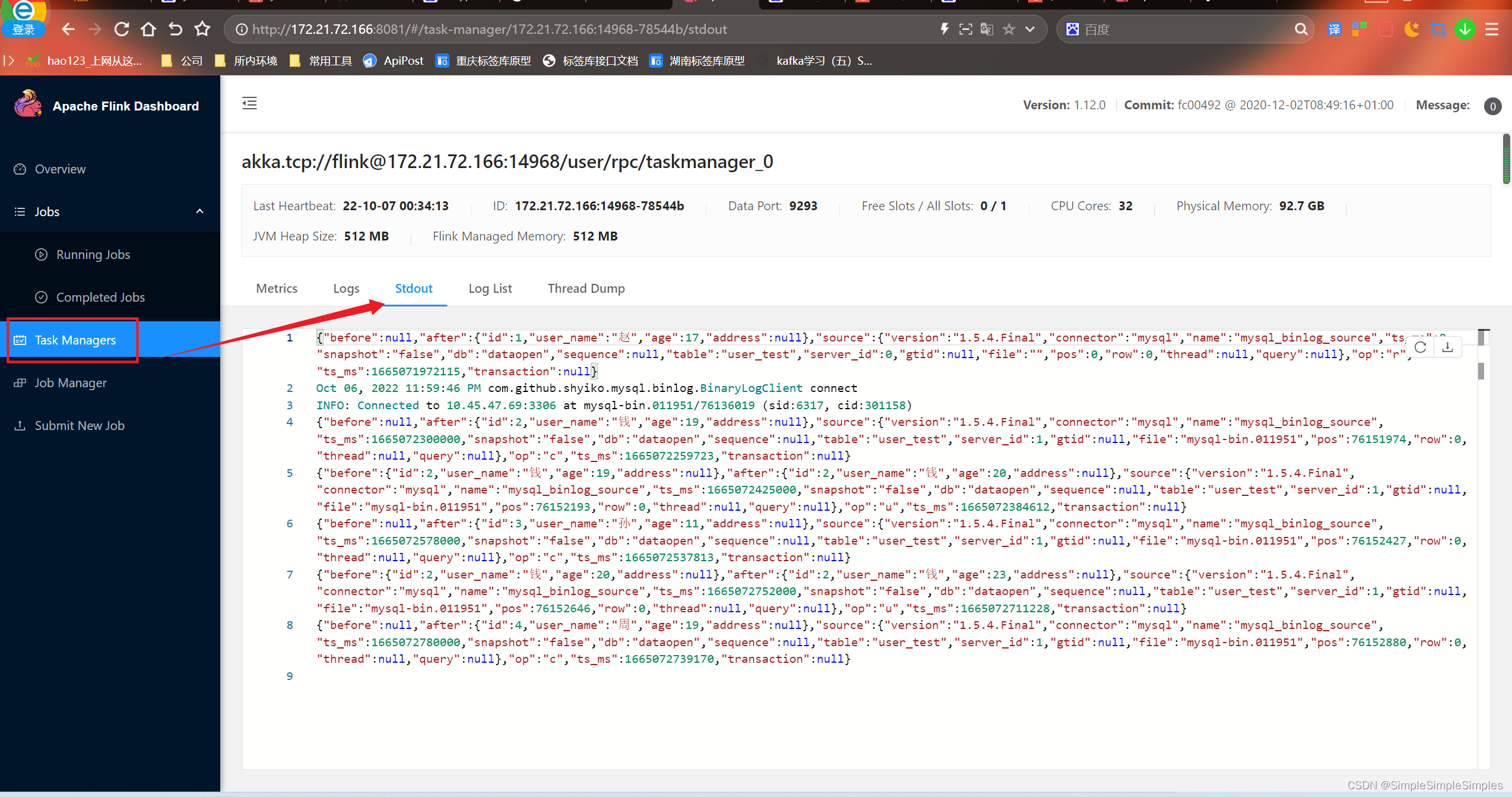
Flink安装与使用
1.安装准备工作 下载flink Apache Flink: 下载 解压 [dodahost166 bigdata]$ tar -zxvf flink-1.12.0-bin-scala_2.11.tgz 2.Flinnk的standalone模式安装 2.1修改配置文件并启动 修改,好像使用默认的就可以了 [dodahost166 conf]$ more flink-conf.yaml 启动 …...
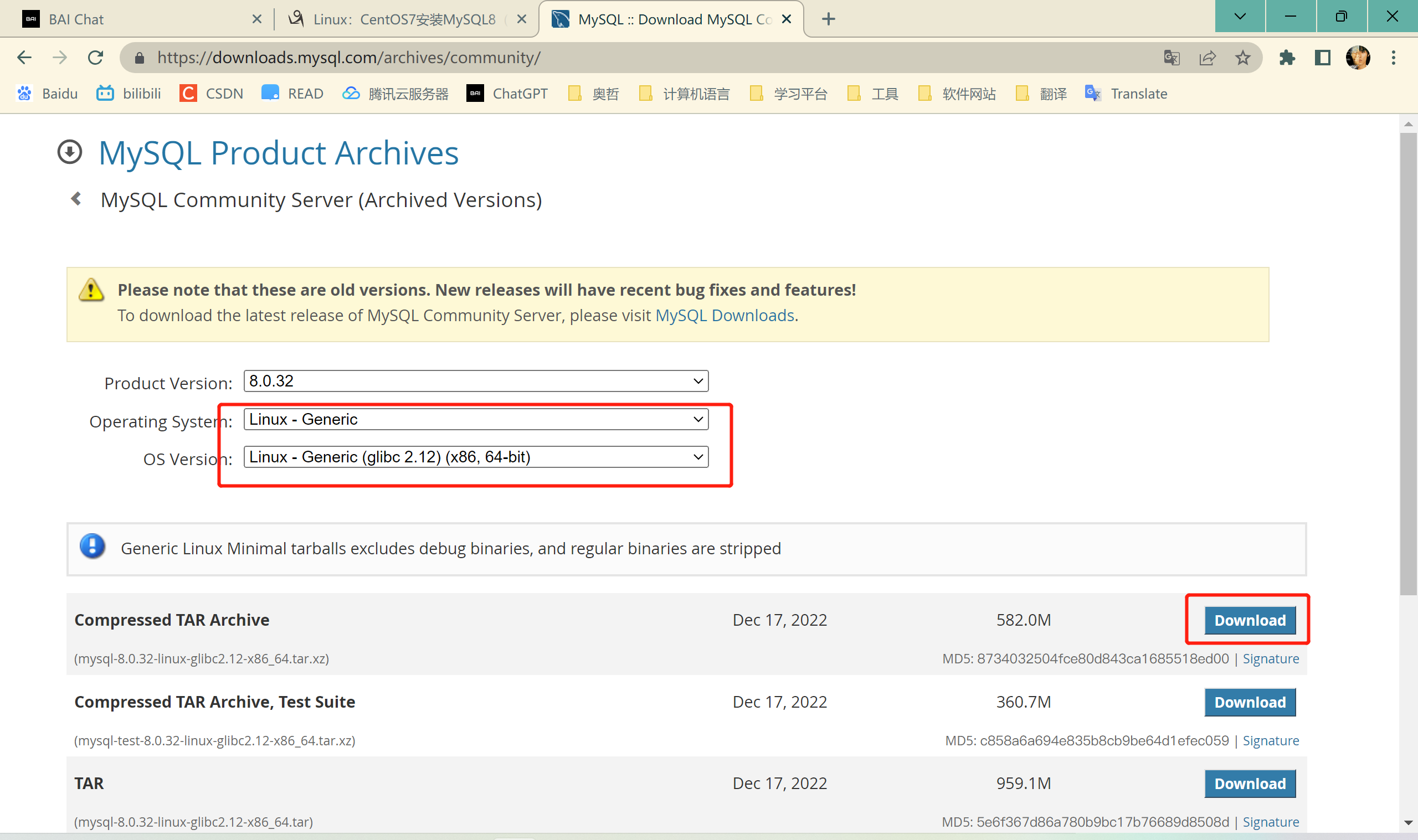
CentOS系统环境搭建(七)——Centos7安装MySQL
centos系统环境搭建专栏🔗点击跳转 坦诚地说,本文中百分之九十的内容都来自于该文章🔗Linux:CentOS7安装MySQL8(详),十分佩服大佬文章结构合理,文笔清晰,我曾经在这篇文章…...

3.react useRef使用与常见问题
react useRef使用与常见问题 文章目录 react useRef使用与常见问题1. Dom操作: useRef()2. 函数组件的转发: React.forwardRef()3. 对普通值进行记忆, 类似于一个class的实例属性4. 结合useEffect,只在更新时触发FAQ 1. Dom操作: useRef() // 1. Dom操作: useRef()let app doc…...

Axios使用CancelToken取消重复请求
处理重复请求:没有响应完成的请求,再去请求一个相同的请求,会把之前的请求取消掉 新增一个cancelRequest.js文件 import axios from "axios" const cancelTokens {}export const addPending (config) > {const requestKey …...

九耶丨阁瑞钛伦特-Spring boot与Spring cloud 之间的关系
Spring Boot和Spring Cloud是两个相互关联的项目,它们可以一起使用来构建微服务架构。 Spring Boot是一个用于简化Spring应用程序开发的框架,它提供了自动配置、快速开发的特性,使得开发人员可以更加轻松地创建独立的、生产级别的Spring应用程…...
总结,由于顺丰的问题,产生了电脑近期一个月死机问题集锦
由于我搬家,我妈搞顺丰发回家,但是没有检查有没有坏,并且我自己由于不可抗力因素,超过了索赔时间,反馈给顺丰客服,说超过了造成了无法索赔的情况,现在总结发生了损坏配件有几件,显卡…...
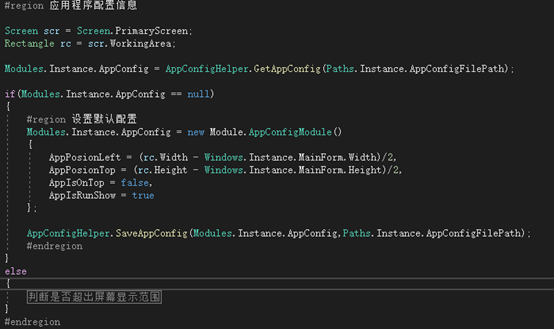
C#程序配置读写例子 - 开源研究系列文章
今天讲讲关于C#的配置文件读写的例子。 对于应用程序的配置文件,以前都是用的ini文件进行读写的,这个与现在的json类似,都是键值对应的,这次介绍的是基于XML的序列化和反序列化的读写例子。对于ini文件,操作系统已经提…...

Angular中的管道Pipes
Angular中的管道(Pipes)是一种强大的工具,它可以处理和转换数据,然后将其呈现在视图中。它们可以被用于排序、格式化和过滤数据等任务。在本文中,我们将介绍Angular中的管道以及如何使用它们来简化开发过程。 管道的基…...
React入门 jsx学习笔记
一、JSX介绍 概念:JSX是 JavaScript XML(HTML)的缩写,表示在 JS 代码中书写 HTML 结构 作用:在React中创建HTML结构(页面UI结构) 优势: 采用类似于HTML的语法,降低学…...

sqlserver数据库中把一张表中的数据复制到另一张表中
我们在使用ERP时经常会遇到,把老系统的单据直接拉过来使用,但是对应的数据却没有,为空,这时候就需要把老系统数据库里的数据复制一份到新系统里,(方法如下) 1、如果是整个表复制表达如下&#…...
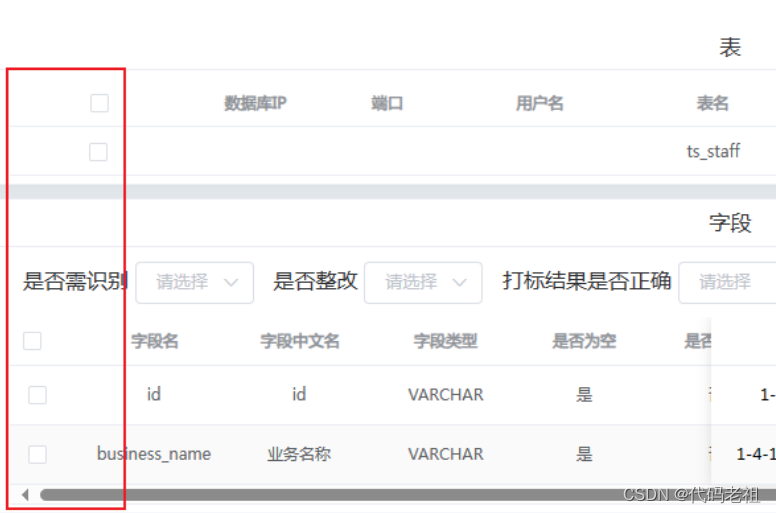
el-table 多个表格切换多选框显示bug
今天写了个功能,点击左侧的树做判断,一级树节点显示系统页面,二级树节点显示数据库页面,三级树节点显示表页面。 数据库页面和表页面分别有2个el-table ,上面的没有多选框,下面的有多选框 现在出现bug,在…...
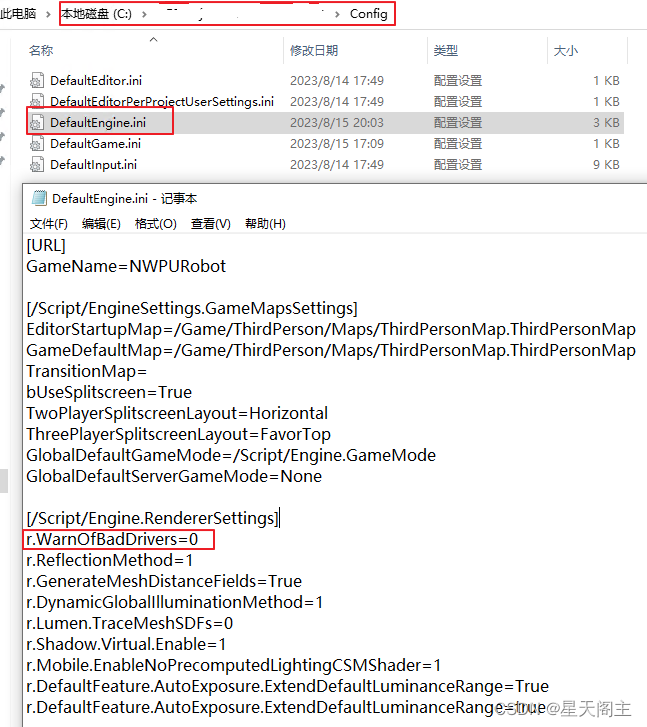
UE5.2程序发布及运行问题记录
发布后的程序默认是以全屏模式启动运行的,通过添加以下命令行参数,可实现程序的窗口模式运行: -ResX1280 -ResY720 -WINDOWED 发布后的程序,启动时,提示显卡驱动警告(如图1所示),但是…...

c语言strtol函数、strtod函数、strtoul函数浅悉
---------------- | strtol | ---------------- i.e. string to long long int strtol(const char *nptr, char **endptr, int base) strtol()会将nptr指向的字符串,根据参数base,按权转化为long int, 然后返回这个值。 参数base的范…...
Spark第三课
1.分区规则 1.分区规则 shuffle 1.打乱顺序 2.重新组合 1.分区的规则 默认与MapReduce的规则一致,都是按照哈希值取余进行分配. 一个分区可以多个组,一个组的数据必须一个分区 2. 分组的分区导致数据倾斜怎么解决? 扩容 让分区变多修改分区规则 3.HashMap扩容为什么必须…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
