平方数之和(力扣)双指针 JAVA
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a^2 + b^2 = c 。
示例 1:
输入:c = 5
输出:true
解释:1 * 1 + 2 * 2 = 5
示例 2:
输入:c = 3
输出:false
提示:
0 <= c <= 2^31 - 1
解题思路:
1、采用双指针在构建的二维矩阵中查找
2、得用long类型变量
3、l = 0, r = Math.sqrt( c )


代码:
class Solution {public boolean judgeSquareSum(int c) {long l = 0, r = (long) Math.sqrt(c);while(l <= r) {if(l * l + r * r > c) r --;else if(l * l + r * r < c) l ++;else return true;}return false;}
}

相关文章:

平方数之和(力扣)双指针 JAVA
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a^2 b^2 c 。 示例 1: 输入:c 5 输出:true 解释:1 * 1 2 * 2 5 示例 2: 输入:c 3 输出&am…...

深入浅出Pytorch函数——torch.nn.init.sparse_
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.nn.init.calculate_gain 深入浅出Pytorch函数——torch.nn.init.uniform_ 深入浅出Pytorch函数——torch.nn.init.normal_ 深入浅出Pytorch函数——torch.nn.init.c…...

OpenCV实现BGR2BayerGB/BG格式的转换
1、说明 OpenCV没有提供从BGR生成Bayer格式的接口,需要自己写 OpenCV定义为4种格式,分别为: BGGR排列 -> RG格式 RGGB排列 -> BG格式 GRBG排列 -> GB格式 GBRG排列 -> GR格式 2、转换 void CUtils::BGR2BayerGB(const cv::Mat &matSrc, cv::Mat &matDst)…...

Gateway网关路由以及predicates用法(项目中使用场景)
1.Gatewaynacos整合微服务 服务注册在nacos上,通过Gateway路由网关配置统一路由访问 这里主要通过yml方式说明: route: config: #type:database nacos yml data-type: yml group: DEFAULT_GROUP data-id: jeecg-gateway-router 配置路由:…...

深入浅出Pytorch函数——torch.nn.init.constant_
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.nn.init.calculate_gain 深入浅出Pytorch函数——torch.nn.init.uniform_ 深入浅出Pytorch函数——torch.nn.init.normal_ 深入浅出Pytorch函数——torch.nn.init.c…...
)
centos mysql8解决Access denied for user ‘root‘@‘localhost‘ (using password: YES)
环境 系统:CentOS Stream release 9 mysql版本:mysql Ver 8.0.34 for Linux on x86_64 问题 mysql登录提示 Access denied for user rootlocalhost (using password: YES)解决方法 编辑 /etc/my.cnf ,在[mysqld] 部分最后添加一行 skip-…...

Docker实战:Docker常用命令
一、镜像相关 1.1、查看镜像 docker images1.2、拉取镜像 docker pull nginx1.3、保存镜像 docker save -o nginx.tar nginx:latest1.4、移除镜像 docker rmi -f nginx:latest1.5、导入镜像 docker load -i nginx.tar二、容器相关 2.1、启动容器 docker run --name red…...
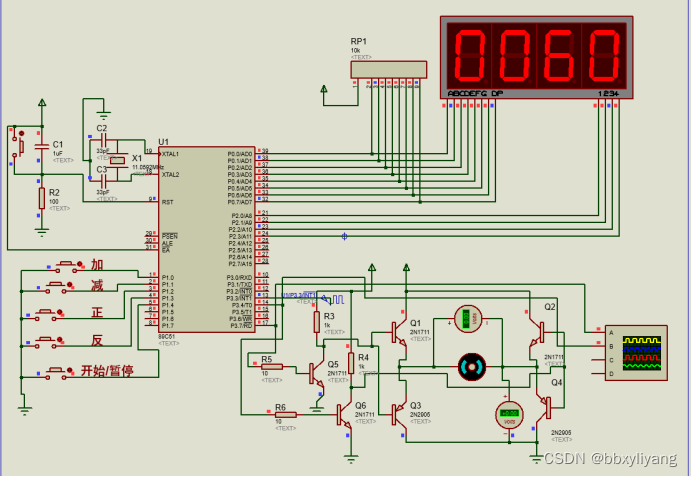
基于51单片机直流电机转速数码管显示控制系统
一、系统方案 本文主要研究了利用MCS-51系列单片机控制PWM信号从而实现对直流电机转速进行控制的方法。本文中采用了三极管组成了PWM信号的驱动系统,并且对PWM信号的原理、产生方法以及如何通过软件编程对PWM信号占空比进行调节,从而控制其输入信号波形等…...
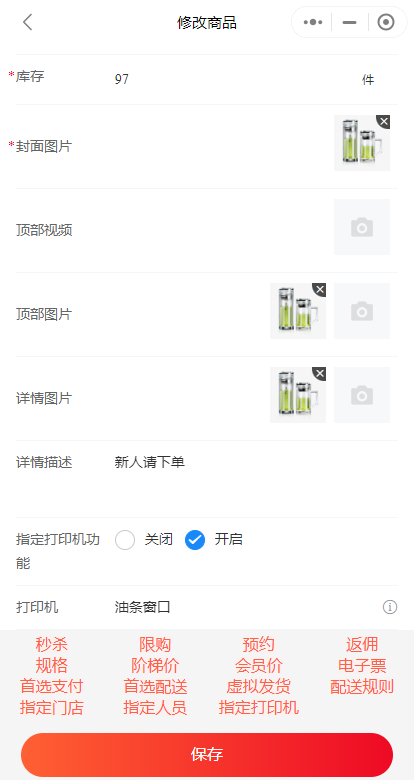
小程序商品如何指定打印机
有些商家,可能有多个仓库。不同的仓库,存放不同的商品。当客户下单时,小程序如何自动按照仓库拆分订单,如何让打印机自动打印对应仓库的订单呢?下面就来介绍一下吧。 1. 设置订单分发模式。进入管理员后台,…...

LLaMA-7B微调记录
Alpaca(https://github.com/tatsu-lab/stanford_alpaca)在70亿参数的LLaMA-7B上进行微调,通过52k指令数据(https://github.com/tatsu-lab/stanford_alpaca/blob/main/alpaca_data.json),在8个80GB A100上训…...
)
域名子目录发布问题(nginx、vue-element-admin、uni-app)
域名子目录发布问题(nginx、vue-element-admin、uni-app) 说明Vue-Element-Admin 代码打包nginx配置:uni-app打包 说明 使用一个域名下子目录进行打包: 比如: http://www.xxx.com/merchant 商户端代码 http://www.xx…...
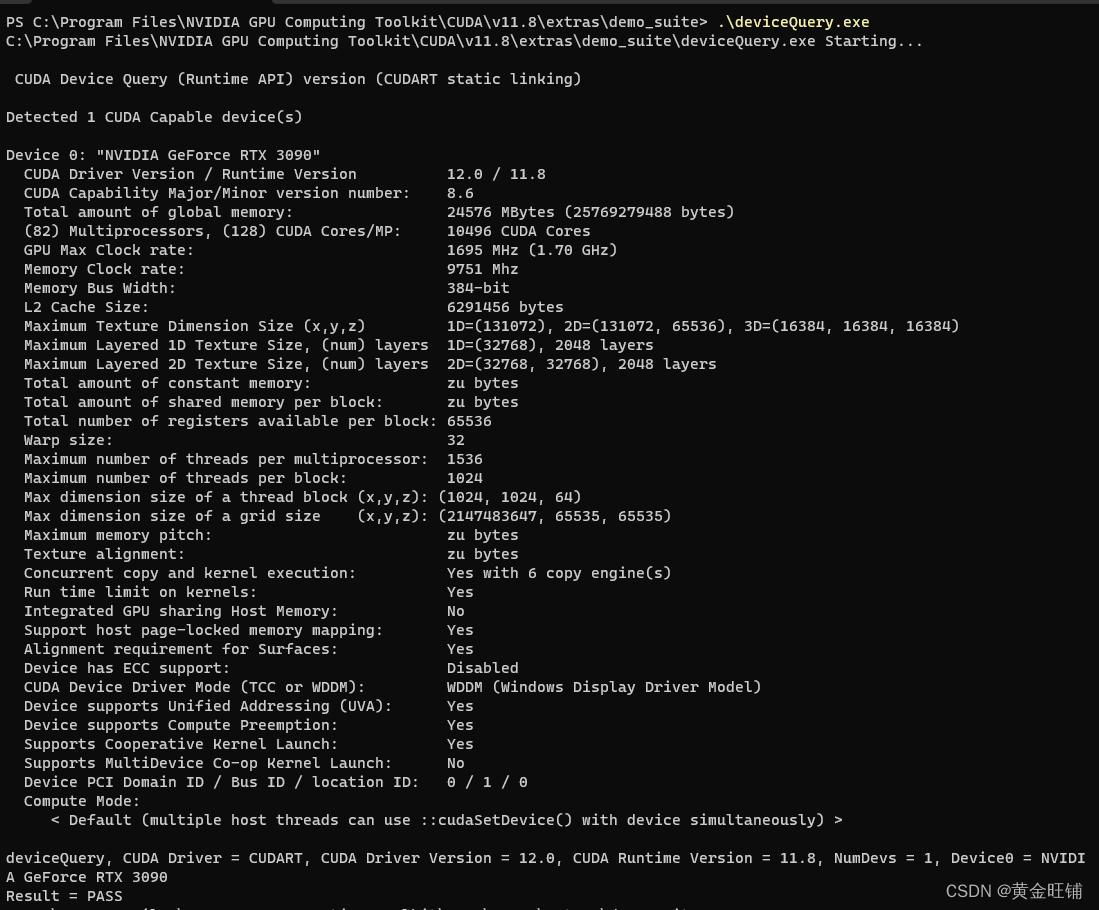
【环境配置】Windows 10 安装 PyTorch 开发环境,以及验证 YOLOv8
Windows 10 安装 PyTorch 开发环境,以及验证 YOLOv8 最近搞了一台Windows机器,准备在上面安装深度学习的开发环境,并搭建部署YOLOv8做训练和测试使用; 环境: OS: Windows 10 显卡: RTX 3090 安…...
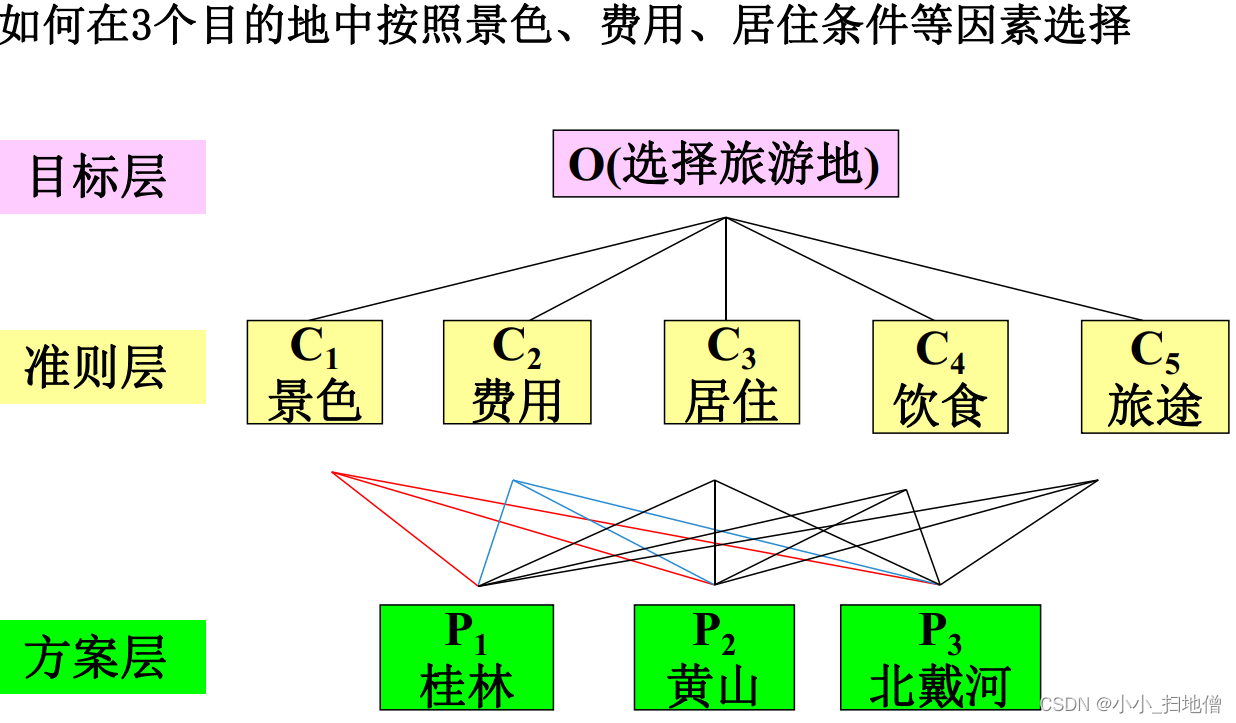
数学建模之“层次分析法”原理和代码详解
一、层次分析法简介 层次分析法(Analytic Hierarchy Process,AHP)是一种用于多准则决策分析和评估问题的定量方法,常用于数学建模中。它是由数学家托马斯赛蒂(Thomas Saaty)开发的。 层次分析法将复杂的决…...

使用IText导出复杂pdf
1、问题描述 需要将发票导出成pdf,要求每页都必须包含发票信息和表头行。 2、解决方法 使用IText工具实现PDF导出 IText8文档:Examples (itextpdf.com) 3、我的代码 引入Itext依赖,我这里用的是8.0.1版本 <dependency><groupId>…...
多线程并发服务器(TCP)
服务器 客户端 结果...
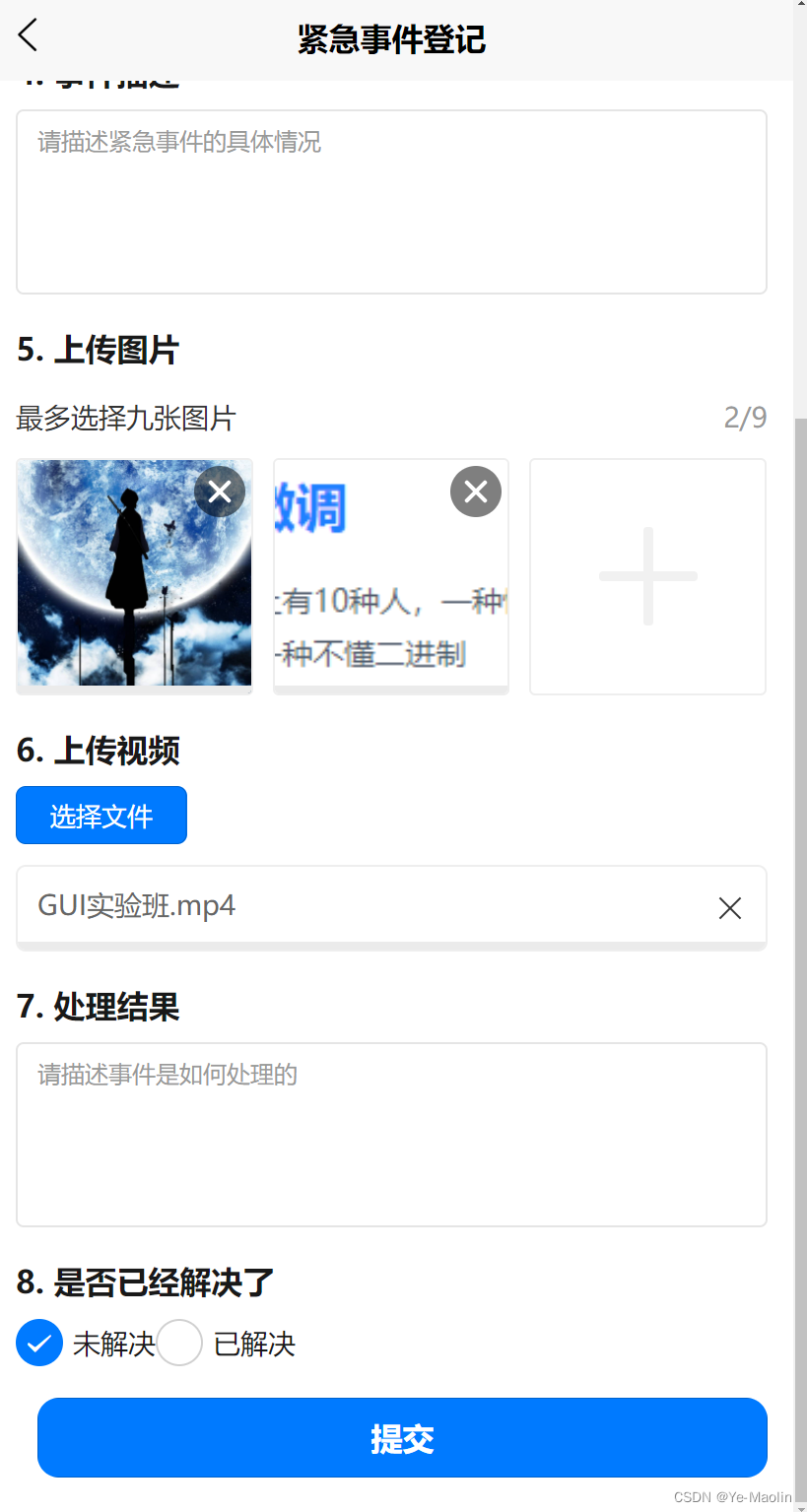
uni-app的Vue.js实现微信小程序的紧急事件登记页面功能
主要功能实现 完成发生时间选择功能,用户可以通过日期选择器选择事件发生的时间。实现事件类型选择功能,用户可以通过下拉选择框选择事件的类型。添加子养殖场编号输入框,用户可以输入与事件相关的子养殖场编号。完成事件描述输入功能&#…...

面试题 17.16.按摩师
题目来源: leetcode题目,网址:面试题 17.16. 按摩师 - 力扣(LeetCode) 解题思路: 动态规划,对于第 i 个预约,若接下,其最大值为不接上一个时的最大值与当前值之和&a…...
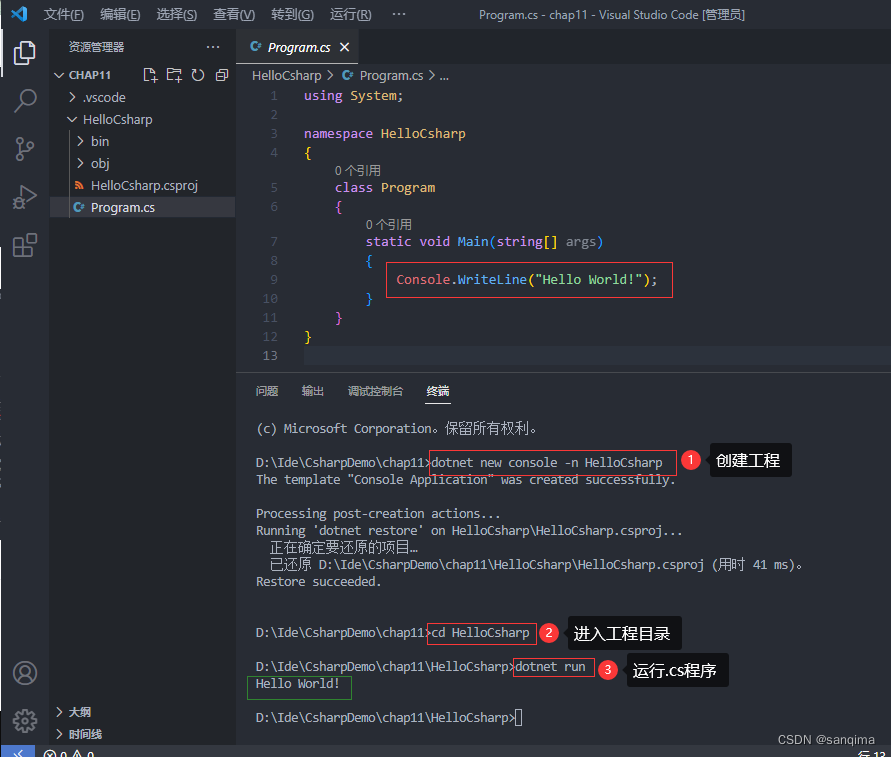
vscode里配置C#环境并运行.cs文件
vscode是一款跨平台、轻量级、开源的IDE, 支持C、C、Java、C#、R、Python、Go、Nodejs等多种语言的开发和调试。下面介绍在vscode里配置C#环境。这里以配置.Net SDK v5.0,语言版本为C#9.0,对应的开发平台为VS2019,作为案例说明。 1、下载vsc…...
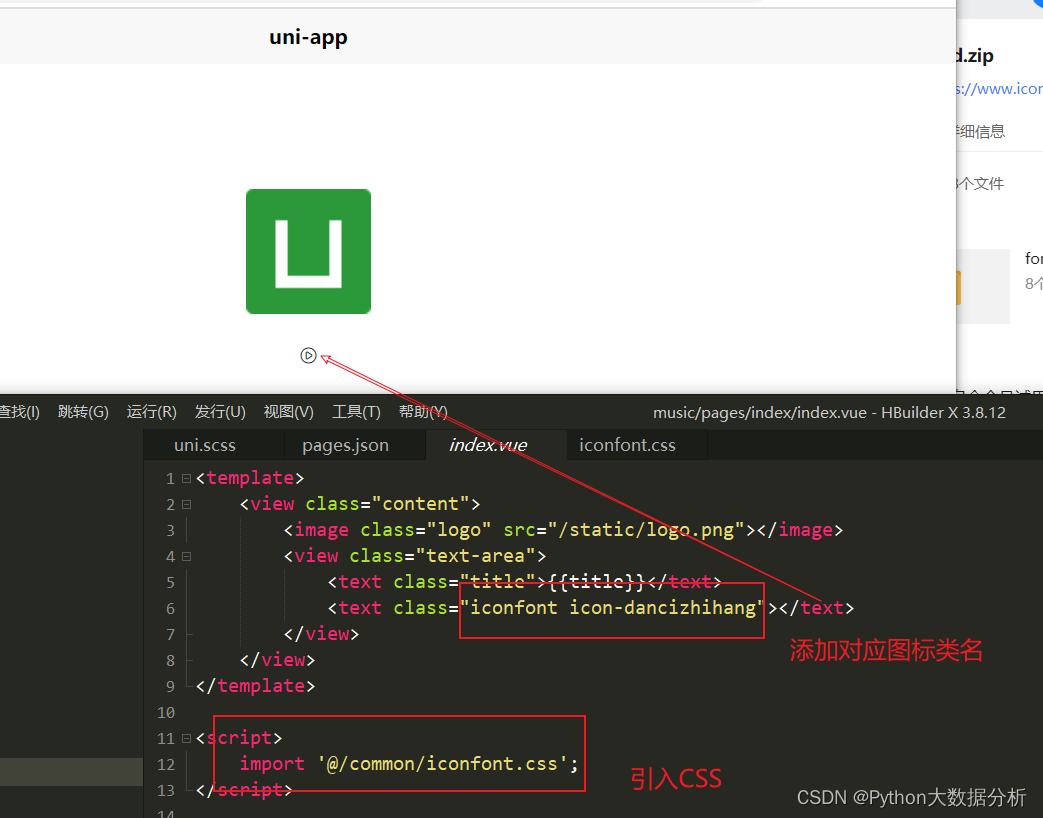
uniapp配置添加阿里巴巴图标icon流程步骤
文章目录 下载复制文件到项目文件夹里项目配置目录结构显示图标 下载 阿里巴巴icon官网 https://www.iconfont.cn/ 复制文件到项目文件夹里 项目配置目录结构 显示图标...
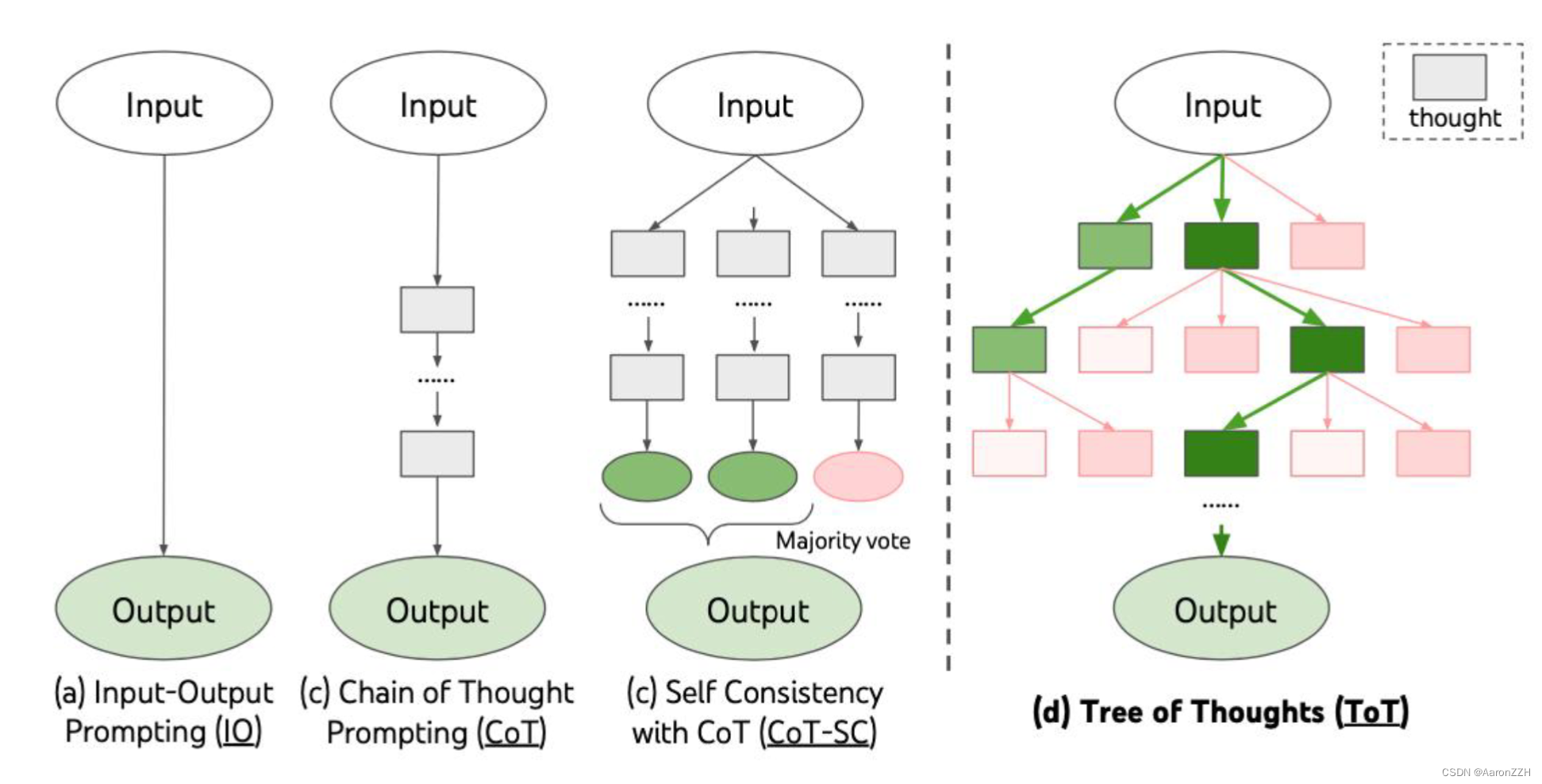
大模型基础02:GPT家族与提示学习
大模型基础:GPT 家族与提示学习 从 GPT-1 到 GPT-3.5 GPT(Generative Pre-trained Transformer)是 Google 于2018年提出的一种基于 Transformer 的预训练语言模型。它标志着自然语言处理领域从 RNN 时代进入 Transformer 时代。GPT 的发展历史和技术特点如下: GP…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...

Neo4j 完全指南:从入门到精通
第1章:Neo4j简介与图数据库基础 1.1 图数据库概述 传统关系型数据库与图数据库的对比图数据库的核心优势图数据库的应用场景 1.2 Neo4j的发展历史 Neo4j的起源与演进Neo4j的版本迭代Neo4j在图数据库领域的地位 1.3 图数据库的基本概念 节点(Node)与关系(Relat…...

【字节拥抱开源】字节团队开源视频模型 ContentV: 有限算力下的视频生成模型高效训练
本项目提出了ContentV框架,通过三项关键创新高效加速基于DiT的视频生成模型训练: 极简架构设计,最大化复用预训练图像生成模型进行视频合成系统化的多阶段训练策略,利用流匹配技术提升效率经济高效的人类反馈强化学习框架&#x…...

Angular中Webpack与ngx-build-plus 浅学
Webpack 在 Angular 中的概念 Webpack 是一个模块打包工具,用于将多个模块和资源打包成一个或多个文件。在 Angular 项目中,Webpack 负责将 TypeScript、HTML、CSS 等文件打包成浏览器可以理解的 JavaScript 文件。Angular CLI 默认使用 Webpack 进行项目…...
Xcode 16.2 版本 pod init 报错
Xcode 版本升级到 16.2 后,项目执行 pod init 报错; ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchron…...

DJango知识-模型类
一.项目创建 在想要将项目创键的目录下,输入cmd (进入命令提示符)在cmd中输入:Django-admin startproject 项目名称 (创建项目)cd 项目名称 (进入项目)Django-admin startapp 程序名称 (创建程序)python manage.py runserver 8080 (运行程序)将弹出的网址复制到浏览器中…...
