中国剩余定理及扩展
目录
中国剩余定理解释
中国剩余定理扩展——求解模数不互质情况下的线性方程组:
代码实现:
互质:
非互质:
中国剩余定理解释
在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?”这个问题称为“孙子问题”,该问题的一般解法国际上称为“中国剩余定理”。具体解法分三步:
-
- 找出三个数:从3和5的公倍数中找出被7除余1的最小数15,从3和7的公倍数中找出被5除余1 的最小数21,最后从5和7的公倍数中找出除3余1的最小数70。
- 用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加15∗2+21∗3+70∗2得到和233。
- 用233除以3,5,7三个数的最小公倍数105,得到余数23,即233%105=23。这个余数23就是符合条件的最小数。
就这么简单。我们在感叹神奇的同时不禁想知道古人是如何想到这个方法的,有什么基本的数学依据吗?
我们将“孙子问题”拆分成几个简单的小问题,从零开始,试图揣测古人是如何推导出这个解法的。
首先,我们假设n1是满足除以3余2的一个数,比如2,5,8等等,也就是满足3∗k+2(k>=0)的一个任意数。同样,我们假设n2是满足除以5余3的一个数,n3是满足除以7余2的一个数。
有了前面的假设,我们先从n1这个角度出发,已知n1满足除以3余2,能不能使得n1+n2的和仍然满足除以3余2?进而使得n1+n2+n3的和仍然满足除以3余2?
这就牵涉到一个最基本数学定理,如果有a%b=c,则有(a+k∗b)%b=c(k为非零整数),换句话说,如果一个除法运算的余数为c,那么被除数与kk倍的除数相加(或相减)的和(差)再与除数相除,余数不变。这个是很好证明的。
以此定理为依据,如果n2是3的倍数,n1+n2就依然满足除以3余2。同理,如果n3也是3的倍数,那么n1+n2+n3的和就满足除以3余2。这是从n1的角度考虑的,再从n2,n3的角度出发,我们可推导出以下三点:
-
- 为使n1+n2+n3的和满足除以3余2,n2和n3必须是3的倍数。
- 为使n1+n2+n3的和满足除以5余3,n1和n3必须是5的倍数。
- 为使n1+n2+n3的和满足除以7余2,n1和n2必须是7的倍数。
因此,为使n1+n2+n3的和作为“孙子问题”的一个最终解,需满足:
- n1除以3余2,且是5和7的公倍数。
- n2除以5余3,且是3和7的公倍数。
- n3除以7余2,且是3和5的公倍数。
所以,孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1,从3和7的公倍数中找一个除以5余3的数n2,从3和5的公倍数中找一个除以7余2的数n3,再将三个数相加得到解。在求n1,n2,n3时又用了一个小技巧,以n1为例,并非从5和7的公倍数中直接找一个除以3余2的数,而是先找一个除以3余1的数,再乘以2。也就是先求出5和7的公倍数模3下的逆元,再用逆元去乘余数。
这里又有一个数学公式,如果a%b=c,那么(a∗k)%b=a%b+a%b+…+a%b=c+c+…+c=k∗c(k>0),也就是说,如果一个除法的余数为c,那么被除数的k倍与除数相除的余数为k∗c。展开式中已证明。
最后,我们还要清楚一点,n1+n2+n3只是问题的一个解,并不是最小的解。如何得到最小解?我们只需要从中最大限度的减掉掉3,5,7的公倍数105即可。道理就是前面讲过的定理“如果a%b=ca%b=c,则有(a−k∗b)%b=c(a−k∗b)%b=c”。所以(n1+n2+n3)%105就是最终的最小解。
这样一来就得到了中国剩余定理的公式:
设正整数
两两互素,则同余方程组
有整数解。并且在模
下的解是唯一的,解为
其中
,而
为
模
的逆元。
中国剩余定理扩展——求解模数不互质情况下的线性方程组:
普通的中国剩余定理要求所有的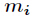
这种情况就采用两两合并的思想,假设要合并如下两个方程:
那么得到:
我们需要求出一个最小的xx使它满足:
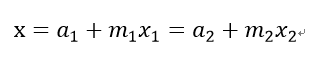
那么x1和x2就要尽可能的小,于是我们用扩展欧几里得算法求出x1的最小正整数解,将它代回a1+m1x1,得到xx的一个特解x′,当然也是最小正整数解。
所以xx的通解一定是x′加上lcm(m1,m2)∗klcm(m1,m2)∗k,这样才能保证x模m1和m2的余数是a1和a2。由此,我们把这个x′当做新的方程的余数,把lcm(m1,m2)当做新的方程的模数。(这一段是关键)
合并完成:
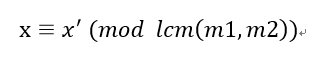
代码实现:
互质:
//求M%A=a,M%B=b,...中的M,其中A,B,C...互质
int CRT(int a[],int m[],int n){ int M = 1; int ans = 0; for(int i=1; i<=n; i++) M *= m[i]; for(int i=1; i<=n; i++){ int x, y; int Mi = M / m[i]; ex_gcd(Mi, m[i], x, y); ans = (ans + Mi * x * a[i]) % M; } if(ans < 0) ans += M; return ans;
} 非互质:
bool merge(LL a1, LL m1, LL a2, LL m2, LL &a3, LL &m3) { LL d = gcd(m1, m2); LL c = a2 - a1; if(c % d) return false; c = (c % m2 + m2) % m2; m1 /= d; m2 /= d; c /= d; c *= Inv(m1, m2);//Inv为乘法逆元,数论常用内容——欧几里得算法与扩展欧几里得算法c %= m2; c *= m1 * d; c += a1; m3 = m1 * m2 * d; a3 = (c % m3 + m3) % m3; return true;
} LL CRT(LL a[], LL m[], int n) { LL a1 = a[1]; LL m1 = m[1]; for(int i=2; i<=n; i++) { LL a2 = a[i]; LL m2 = m[i]; LL m3, a3; if(!merge(a1, m1, a2, m2, a3, m3)) return -1; a1 = a3; m1 = m3; } return (a1 % m1 + m1) % m1;
} 参考:数论常用内容——中国剩余定理
下一篇:Codeforces Round 153 (Rated for Div. 2)
推荐音乐:沉沦于遐想
相关文章:
中国剩余定理及扩展
目录 中国剩余定理解释 中国剩余定理扩展——求解模数不互质情况下的线性方程组: 代码实现: 互质: 非互质: 中国剩余定理解释 在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二&#x…...

数据在内存中的存储(deeper)
数据在内存中的存储(deeper) 一.数据类型的详细介绍二.整形在内存中的存储三.浮点型在内存中的存储 一.数据类型的详细介绍 类型的意义: 使用这个类型开辟内存空间的大小(大小决定了使用范围)如何看待内存空间的视角…...

算法修炼Day52|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
LeetCode:300.最长递增子序列 300. 最长递增子序列 - 力扣(LeetCode) 1.思路 dp[i]的状态表示以nums[i]为结尾的最长递增子序列的个数。 dp[i]有很多个,选择其中最大的dp[i]Math.max(dp[j]1,dp[i]) 2.代码实现 1class Solution {2 pub…...

使用 HTML、CSS 和 JavaScript 创建实时 Web 编辑器
使用 HTML、CSS 和 JavaScript 创建实时 Web 编辑器 在本文中,我们将创建一个实时网页编辑器。这是一个 Web 应用程序,允许我们在网页上编写 HTML、CSS 和 JavaScript 代码并实时查看结果。这是学习 Web 开发和测试代码片段的绝佳工具。我们将使用ifram…...

百望云联合华为发布票财税链一体化数智解决方案 赋能企业数字化升级
随着数据跃升为数字经济关键生产要素,数据安全成为整个数字化建设的重中之重。为更好地帮助企业发展,中央及全国和地方政府相继出台了多部与数据相关的政策法规,鼓励各领域服务商提供具有自主创新的软件产品与服务,帮助企业在合规…...

实现两个栈模拟队列
实现两个栈模拟队列 思路:可以想象一下左手和右手,两个栈:stack1(数据所在的栈) ,stack2(临时存放)。 入队:需要将入队 num 加在 stack1 的栈顶即可; 出队&am…...

无涯教程-TensorFlow - 单词嵌入
Word embedding是从离散对象(如单词)映射到向量和实数的概念,可将离散的输入对象有效地转换为有用的向量。 Word embedding的输入如下所示: blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259) blues: (0.01396, 0.11887, -0.48963, ..., 0.03…...
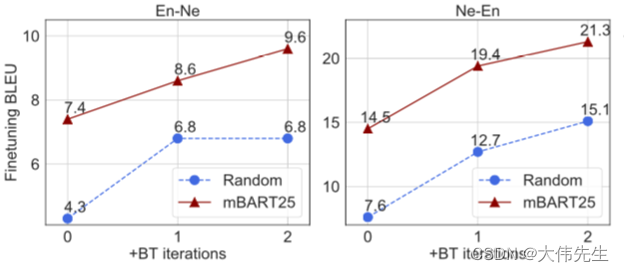
Facebook AI mBART:巴别塔的硅解
2018年,谷歌发布了BERT(来自transformers的双向编码器表示),这是一种预训练的语言模型,在一系列自然语言处理(NLP)任务中对SOTA结果进行评分,并彻底改变了研究领域。类似的基于变压器…...

BDA初级分析——SQL清洗和整理数据
一、数据处理 数据处理之类型转换 字符格式与数值格式存储的数据,同样是进行大小排序, 会有什么区别? 以rev为例,看看字符格式与数值格式存储时,排序会有什么区别? 用cast as转换为字符后进行排序 SEL…...

汽车后视镜反射率测定仪
后视镜是驾驶员坐在驾驶室座位上直接获取汽车后方、侧方和下方等外部信息的工具。它起着“第三只眼睛”的作用。后视镜按安装位置划分通常分为车外后视镜、监视镜和内后视镜。外后视镜观察汽车后侧方监视镜观察汽车前下方内后视镜观察汽车后方及车内情况。用途不一样镜面结构也…...

Redis学习笔记
redis相关内容 默认端口6379 默认16个数据库,初始默认使用0号库 使用select 切换数据库 统一密码管理,所有库密码相同 dbsize:查看当前库key的数量 flushdb:清空当前库 flushall:清空全部库 redis是单线程 多路…...

韩顺平Linux 四十四--
四十四、rwx权限 权限的基本介绍 输入指令 ls -l 显示的内容如下 -rwxrw-r-- 1 root 1213 Feb 2 09:39 abc0-9位说明 第0位确定文件类型(d , - , l , c , b) l 是链接,相当于 windows 的快捷方式- 代表是文件是普通文件d 是目录,相…...

【支付宝小程序】分包优化教程
🦖我是Sam9029,一个前端 Sam9029的CSDN博客主页:Sam9029的博客_CSDN博客-JS学习,CSS学习,Vue-2领域博主 🐱🐉🐱🐉恭喜你,若此文你认为写的不错,不要吝啬你的赞扬,求收…...
语言基础2 矩阵和数组
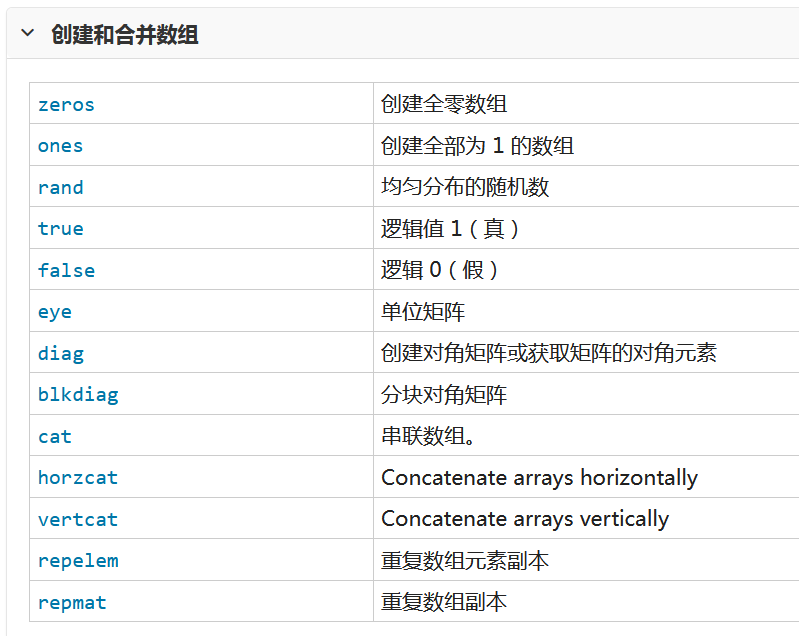
语言基础2 矩阵和数组 矩阵和数组是matlab中信息和数据的基本表示形式 可以创建常用的数组和网格 合并现有的数组 操作数组的形状和内容 以及使用索引访问数组元素 用到的函数列表如下 一 创建 串联和扩展矩阵 矩阵时按行和列排列的数据元素的二维数据元素的二维矩…...

springMVC中过滤器抛出异常,自定义异常捕获
在过滤器中引入org.springframework.web.servlet.HandlerExceptionResolver AutowiredQualifier("handlerExceptionResolver")private HandlerExceptionResolver resolver; // doFilter中处理if (条件1) {if (条件2) {resolver.resolveException(request, response, …...

图像检索技术研究:深度度量与深度散列在相似性学习中的应用比较与实践 - 使用Python与Jupyter环境
引言 在计算机视觉领域,图像检索是一个长期存在并持续受到研究者关注的重要话题。随着大数据时代的到来,如何高效、准确地从海量数据中检索到相似的图像成为一个巨大的挑战。传统的检索方法在大数据环境下表现不佳,而深度学习技术的崛起为图…...

CSS加载失败的6个原因
有很多刚刚接触 CSS 的新手有时会遇到 CSS 加载失败这个问题,但测试时,网页上没有显示该样式的问题,这就说明 CSS 加载失败了。出现这种状况一般是因为的 CSS 路径书写错,或者是在浏览器中禁止掉了 CSS 的加载,可以重新…...
react之路由的安装与使用
一、路由安装 路由官网2021.11月初,react-router 更新到 v6 版本。使用最广泛的 v5 版本的使用 npm i react-router-dom5.3.0二、路由使用 2.1 路由的简单使用 第一步 在根目录下 创建 views 文件夹 ,用于放置路由页面 films.js示例代码 export default functio…...

基于RoCE的应用程序的MTU注意事项
目录 基于RoCE的应用程序的MTU注意事项 探测网络中的MTU设置 概要 原文 MTU测试结果 DOC: CentOS安装tshark抓包工具 基于RoCE的应用程序的MTU注意事项 原文:https://support.mellanox.com/s/article/MLNX2-117-1682kn InfiniBand协议最大传输单元ÿ…...

springboot集成Graphql相关问题汇总
1、idea在debug运行时出现java.lang.NoClassDefFoundError:kotlin/collections/AbstractMutableMap 解决:禁用idea dubugger中kotlin coroutine agent 见:https://stackoverflow.com/questions/70796177/after-the-spring-boot-source-code-is-compile…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...