找到所有数组中消失的数(C语言详解)
题目:找到所有数组中消失的数
题目详情:
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1,n] 内。请你找出所以在 [1,n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
示例1:
输入:nums = [ 4,3,2,7,8,2,3,1 ]
输出:[ 5,6 ]
示例2:
输入:nums = [ 1,1 ]
输出:[ 2 ]
提示:
n=nums.length
1<=n<=105
1<=nums[i]<=n
解法一(非原地修改法)
解题思路:
由题可得给定的数组都是在 [1, n] 范围内的数字,由此我们可以定义一个数组 arr 将 [1, n] 按顺序存起来,此时无论什么数它所对应的下标都是本身减一;
然后我们就想啊,arr 的范围大小是包含于 nums 的,而且 nums 里的整数在 arr 里对应的整数的下标都是其整数减一,所以我们可以做标记来解决本题;
遍历 nums 数组,arr 中凡是在 nums 中出现过的整数都做标记-----记为0,最后 arr 数组中不为0的数字就是消失的数字;
思路实现:
定义数组 arr 并赋值;
int i=0;int arr[100000]={0};for(i=0;i<numsSize;i++){arr[i]=i+1;}然后遍历 nums 数组,找到 arr 中与之相对应的数的下标,并将此下标处的数记为0,比如:nums[2]=4,则 arr 中对应 4 的下标为 nums[2] -1=3,然后arr[nums[2] -1]=0;
for(i=0;i<numsSize;i++){arr[nums[i]-1]=0;}创建一个动态内存变量 ret ,用来存放消失的数字;
遍历 arr 数组不为0的就是消失的数字并存放在 ret 中;
int* ret=(int*)malloc(4*numsSize);int k=0;for(i=0;i<numsSize;i++){if(arr[i]>0){ret[k++]=arr[i];}}此时 ret 中存放的数字就是消失的数字了,返回 ret 即可;
源代码:
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){int* ret=(int*)malloc(4*numsSize);int i=0;int arr[100000]={0};for(i=0;i<numsSize;i++){arr[i]=i+1;}for(i=0;i<numsSize;i++){arr[nums[i]-1]=0;}int k=0;for(i=0;i<numsSize;i++){if(arr[i]>0){ret[k++]=arr[i];}}* returnSize=k;return ret;
}解法二(原地修改法)
解题思路:
其实跟解法一有异曲同工之妙,就是在解法一的基础上不使用 arr 数组,自身解决,一样的意思的,解法一它后面侧重判断的点是 arr 的数值,而我们解法二是原地修改,侧重的是下标的数值,具体如何,听博主慢慢分晓;
在数组 nums 中,有着 n 个数字,数字之间可能会重复,一旦重复就会产生消失的数字,此时我们将数组 nums 的数值与下标分离开来,然后遍历 nums ,然后将下标为 nums[i]-1的值加上 n ,如果 nums[i]-1大于 n,需要对其取模来还原出他本来的值;
然后在创建动态内存变量 ret 来存储消失的数字,遍历数组 nums ,如果数字不大于n,则此下标加一就是消失的数字的;
思路实现:
遍历数组 nums ,将下标为 nums[i]-1的值加上 n,如果此值大于 n ,需要对其取模来还原,即将下标为(nums[i]-1)%n 的值加上 n;
int i=0;for(i=0;i<numsSize;i++){nums[(nums[i]-1)%numsSize]+=numsSize;}创建一个动态内存变量 ret ,用来存放消失的数字;
遍历 nums 数组不大于 n 的数字的下标加一就是消失的数字;
int* ret=(int*)malloc(4*numsSize);int i=0;int k=0;for(i=0;i<numsSize;i++){if(nums[i]<=numsSize){ret[k++]=i+1;}}此时 ret 中存放的数字就是消失的数字了,返回 ret 即可;
源代码:
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){int* ret=(int*)malloc(4*numsSize);int i=0;for(i=0;i<numsSize;i++){nums[(nums[i]-1)%numsSize]+=numsSize;}int k=0;for(i=0;i<numsSize;i++){if(nums[i]<=numsSize){ret[k++]=i+1;}}* returnSize=k;return ret;
}以上就是本题的两种解法,其实都不算很复杂,就是得画图得想到这里,如果现在还不具备此思维也不要慌张正常现象而已,多刷题锻炼思维即可;
如有不足之处欢迎来补充交流!
完结。。。
相关文章:
)
找到所有数组中消失的数(C语言详解)
题目:找到所有数组中消失的数 题目详情: 给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1,n] 内。请你找出所以在 [1,n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 示例1: 输入…...
计算机毕设项目之基于django+mysql的疫情实时监控大屏系统(前后全分离)
系统阐述的是一款新冠肺炎疫情实时监控系统的设计与实现,对于Python、B/S结构、MySql进行了较为深入的学习与应用。主要针对系统的设计,描述,实现和分析与测试方面来表明开发的过程。开发中使用了 django框架和MySql数据库技术搭建系统的整体…...

Unity UI内存泄漏优化
项目一运行,占用的内存越来越多,不会释放,导致GC越来越频繁,越来越慢,这些都是为什么呢,今天从UI方面谈起。 首先让我们来聊聊什么是内存泄漏呢? 一般来讲内存泄漏就是指我们的应用向内存申请…...

学习笔记:Opencv实现图像特征提取算法SIFT
2023.8.19 为了在暑假内实现深度学习的进阶学习,特意学习一下传统算法,分享学习心得,记录学习日常 SIFT的百科: SIFT Scale Invariant Feature Transform, 尺度不变特征转换 全网最详细SIFT算法原理实现_ssift算法_Tc.小浩的博客…...
使用和原理)
【golang】接口类型(interface)使用和原理
接口类型的类型字面量与结构体类型的看起来有些相似,它们都用花括号包裹一些核心信息。只不过,结构体类型包裹的是它的字段声明,而接口类型包裹的是它的方法定义。 接口类型声明中的这些方法所代表的就是该接口的方法集合。一个接口的方法集…...

【Linux操作系统】Linux系统编程中的共享存储映射(mmap)
在Linux系统编程中,进程之间的通信是一项重要的任务。共享存储映射(mmap)是一种高效的进程通信方式,它允许多个进程共享同一个内存区域,从而实现数据的共享和通信。本文将介绍共享存储映射的概念、原理、使用方法和注意…...
2235.两整数相加:19种语言解法(力扣全解法)
【LetMeFly】2235.两整数相加:19种语言解法(力扣全解法) 力扣题目链接:https://leetcode.cn/problems/add-two-integers/ 给你两个整数 num1 和 num2,返回这两个整数的和。 示例 1: 输入:num…...
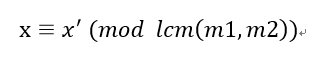
中国剩余定理及扩展
目录 中国剩余定理解释 中国剩余定理扩展——求解模数不互质情况下的线性方程组: 代码实现: 互质: 非互质: 中国剩余定理解释 在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二&#x…...

数据在内存中的存储(deeper)
数据在内存中的存储(deeper) 一.数据类型的详细介绍二.整形在内存中的存储三.浮点型在内存中的存储 一.数据类型的详细介绍 类型的意义: 使用这个类型开辟内存空间的大小(大小决定了使用范围)如何看待内存空间的视角…...

算法修炼Day52|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
LeetCode:300.最长递增子序列 300. 最长递增子序列 - 力扣(LeetCode) 1.思路 dp[i]的状态表示以nums[i]为结尾的最长递增子序列的个数。 dp[i]有很多个,选择其中最大的dp[i]Math.max(dp[j]1,dp[i]) 2.代码实现 1class Solution {2 pub…...

使用 HTML、CSS 和 JavaScript 创建实时 Web 编辑器
使用 HTML、CSS 和 JavaScript 创建实时 Web 编辑器 在本文中,我们将创建一个实时网页编辑器。这是一个 Web 应用程序,允许我们在网页上编写 HTML、CSS 和 JavaScript 代码并实时查看结果。这是学习 Web 开发和测试代码片段的绝佳工具。我们将使用ifram…...

百望云联合华为发布票财税链一体化数智解决方案 赋能企业数字化升级
随着数据跃升为数字经济关键生产要素,数据安全成为整个数字化建设的重中之重。为更好地帮助企业发展,中央及全国和地方政府相继出台了多部与数据相关的政策法规,鼓励各领域服务商提供具有自主创新的软件产品与服务,帮助企业在合规…...

实现两个栈模拟队列
实现两个栈模拟队列 思路:可以想象一下左手和右手,两个栈:stack1(数据所在的栈) ,stack2(临时存放)。 入队:需要将入队 num 加在 stack1 的栈顶即可; 出队&am…...

无涯教程-TensorFlow - 单词嵌入
Word embedding是从离散对象(如单词)映射到向量和实数的概念,可将离散的输入对象有效地转换为有用的向量。 Word embedding的输入如下所示: blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259) blues: (0.01396, 0.11887, -0.48963, ..., 0.03…...
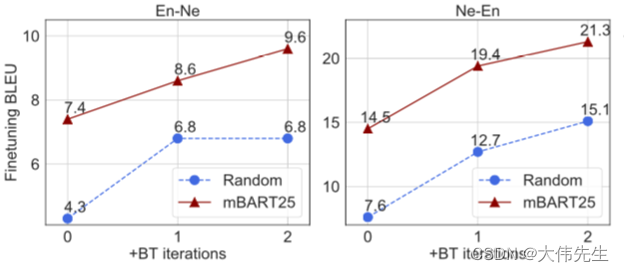
Facebook AI mBART:巴别塔的硅解
2018年,谷歌发布了BERT(来自transformers的双向编码器表示),这是一种预训练的语言模型,在一系列自然语言处理(NLP)任务中对SOTA结果进行评分,并彻底改变了研究领域。类似的基于变压器…...

BDA初级分析——SQL清洗和整理数据
一、数据处理 数据处理之类型转换 字符格式与数值格式存储的数据,同样是进行大小排序, 会有什么区别? 以rev为例,看看字符格式与数值格式存储时,排序会有什么区别? 用cast as转换为字符后进行排序 SEL…...

汽车后视镜反射率测定仪
后视镜是驾驶员坐在驾驶室座位上直接获取汽车后方、侧方和下方等外部信息的工具。它起着“第三只眼睛”的作用。后视镜按安装位置划分通常分为车外后视镜、监视镜和内后视镜。外后视镜观察汽车后侧方监视镜观察汽车前下方内后视镜观察汽车后方及车内情况。用途不一样镜面结构也…...

Redis学习笔记
redis相关内容 默认端口6379 默认16个数据库,初始默认使用0号库 使用select 切换数据库 统一密码管理,所有库密码相同 dbsize:查看当前库key的数量 flushdb:清空当前库 flushall:清空全部库 redis是单线程 多路…...

韩顺平Linux 四十四--
四十四、rwx权限 权限的基本介绍 输入指令 ls -l 显示的内容如下 -rwxrw-r-- 1 root 1213 Feb 2 09:39 abc0-9位说明 第0位确定文件类型(d , - , l , c , b) l 是链接,相当于 windows 的快捷方式- 代表是文件是普通文件d 是目录,相…...

【支付宝小程序】分包优化教程
🦖我是Sam9029,一个前端 Sam9029的CSDN博客主页:Sam9029的博客_CSDN博客-JS学习,CSS学习,Vue-2领域博主 🐱🐉🐱🐉恭喜你,若此文你认为写的不错,不要吝啬你的赞扬,求收…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
