算法通关村十一关 | 位运算的规则
1.数字在计算机中的表示
-
机器数:一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是自带符号的,在计算机用一个数的最高位存放符号,整数为0,负数为1。比如,十进制中的数+3,计算机字长8位,转换成二进制就是00000011.如果是-3.就是10000011。两者都是机器数。
-
真值:因为机器数的第一位是符号位,所以机器数的形式值就不等于真正的数值。例如上面的有符号数10000011,其实最高位1代表负,其真正数值是-3,而不是形式数值131(10000011转换成10进制等于131)。所以将带符号位的机器数对应的的真正数值称为机器数的真值。(0000 0001的真值 = +000 0001 = +1,1000 0001的真值 = -000 0001 = -1)。
计算机对机器数的表示进一步细化:原码,反码,补码。
-
原码就是符号位加上真值的绝对值,即用第一位表示符号,其余位表示值,比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位所以8进制的取值范围是
[1111 1111, 0111 1111] 即[-127 , 127]
-
反码的表示方法是:正数的反码是其本身,负数的反码在原码的基础上,符号位不变,其它位取反。
[+1] = [0000 0001]原 = [0000 0001]反
[-1] = [1000 0001]原 = [1111 1110]反
可以发现一个反码表示的是负数,人脑无法直观的看出来它的数值,通常要将其转换成原码再计算。
因为补码能保持加和减运算的统一,因此应用更广,其表示方法是:
-
正数的补码就是其本身
-
负数的补码是在反码的基础上加1
对于负数,补码也需要转换成原码在计算其数值
拓展为何会有原码、反码和补码?
[+1] = [0000 0001]原 = [0000 0001]反 = [0000 0001]补
[-1] = [1000 0001]原 = [1111 1110]反 = [1111 1111]补
我们都知道计算机中只有加法,我们看个例子,计算十进制的表达式:1-1=0,看原码表示:
1- 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [1000 0010]原 = -2
结果不正确
用反码计算:
1- 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原
= [0000 0001]反 + [1111 1110]反
=[1111 1111]反 = [1000 0000] 原 =-0
有点奇怪,0带符号没有意义
用补码计算:
1- 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原
= [0000 0001]补 + [1111 1111]补
=[0000 0000] 补+[0000 0000]原 = 0
负0就不存在了,可以用[1000 0000] 表示-128。补码的表示范围就是[-128 - 127]
-
2.位运算规则
2.1与、或、异或和取反
-
与运算 & ,规则:对于每个二进制位,两个数都为1,结果才为1,否则结果为0.
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1
-
或运算 | ,规则:对于每个二进制位,两个数都为0时,结果才为0,否则结果为1.
0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
-
异或运算的符号价⊕(在代码中用^表示),相同为0,不同为1
0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 0
-
取反运算符号 ~,运算规则,0变1,1变0,
2.2 移位运算
-
移位运算分为左移和右移,按照是否带符号可以分成算术运算和逻辑移位。
原始:0000 0110 6
右移一次:0000 0011 3 相当于除以2
左移一次:0000 1100 12 相当于乘于2
-
左移运算的符号是<< ,左移运算时,将全部运算时,将全部二进制位向左移动若干位,高位丢弃,低位补0。对于左移运算,算术移位和逻辑移位是相同的。
-
右移运算的符号是>>,右移运算时,将全部的二进制位向右移动若干位,低位丢弃,高位的补位由算术移位或逻辑移位决定:
-
算术移位时,高位补最高位,(负数最高位补1,正数补0)
-
逻辑右移时,高位补0
在计算机中,对于0和正数,算术移位和逻辑移位结果是相同的。负数的结果时不同的。
对于C++,数据类型包含有符号和无符号类型。有符号类型右移为算术右移,无符号类型右移运算为逻辑右移。
对于Java,不存在无符号类型,算术右移是>>,逻辑右移是>>>
-
2.3 移位运算与乘除法的关系
-
左移运算对应乘法关系。低位补0,将一个数左移k位,相当于这个数乘于2^k.
-
右移运算对应除法关系,将一个数右移k位,相当于这个数除以2^k.
需要注意的是:
-
左移无需考虑太多只需低位补0即可。
-
对于负数和正数的右移对应的结果是不一致的,分为算术右移和逻辑右移。算法在出题的时候考虑到这一点,大部分会将数据限制在正数和0的情况 ,因此可以放心的左移或右移。
-
2.4 位运算技巧
位运算的性质有很多,有一些运算公式,
-
幂等律:a&a=a, a | a = a (注意异或运算不满足幂等率)
-
交换律:a & b = b & a, a| b = b | a, a ⊕ b = b ⊕ a
-
结合律:( a & b) & c = a& ( b& c) ,(a | b) | c = a | ( b | c),(a ⊕ b) & c = a ⊕( b ⊕ c)
-
分配律:(a & b) | c = ( a & c) & ( b & c) ,(a | b) & c = (a & b) | ( b& c) ,异或同理
-
德摩根律:~(a & b)= ( ~a) | (~ b), ~(a | b) = (~a) & (~b)
-
取反运算性质:-1 = ~0, -a = ~( a - 1)
-
与运算性质:a & 0 = a, a& (~1) = a,a & (~a) = 0;
-
或运算性质: a | 0 = a, a | ( ~ a) = -1 ;
-
异或运算性质: a⊕0 = a, a⊕a = 0;
根据上面的性质可以得到很多的处理技巧,
-
a & (a - 1) 的结果位将a的二进制表示的最后一个1变为0;
-
(补码)a&(-a) 的结果为只保留a的二进制表示的最后一个,其余的1都变成0.
如何获取、设置、和更新某个位的数据,也有固定的套路。
-
获取
该方法是将1左移i位,得到形如00010000的值,接着对这个值与num执行“位与”操作,从而将i位之外的所有位清零,最后检查该结果是否为零。不为零i位为1,否则i位位0。代码如下:
boolean getBit(int num, int i) {
return ((num & (1 << i))) != 0;
}
-
设置(将某一位置设置为1)
setBit先将1右移i位,得到形如00010000的值,接着对这个值和num执行“位或”操作,这样只会改变i位的数据。除i位外的位均为零,故不会影响num的其余位。代码如下:
int setBIt(int num, int i) {
return num | (i << i);
}
-
清零(将某一位置设置为0)
该方法与setBit方法相反,首先将1左移i位获得形如00010000的值,对这个值取反的到类似11101111的值,接着对该值和num执行“位与”,古不会影响到num的其余位,只会清零i位。代码如下:
int clearBit(int num, int i) {
int mask = ~(1 << i); return num & mask;
}
-
更新
这个方法是将setBit和clearBit合二为一,首先用11101111的值num的第i位清零,接着将待写入的值v左移i位,得到一个i位为v但其余为都为0的数。最后对之前的结果执行“位或”操作,v为1则num的i位更新为1,否则为0.代码如下:
int updateBit(int num, int i, int v) {
int mask = ~(1 << i); return (num & mask) | (v << i);
}
相关文章:

算法通关村十一关 | 位运算的规则
1.数字在计算机中的表示 机器数:一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是自带符号的,在计算机用一个数的最高位存放符号,整数为0,负数为1。比如,十进制中的数3,计算机字…...
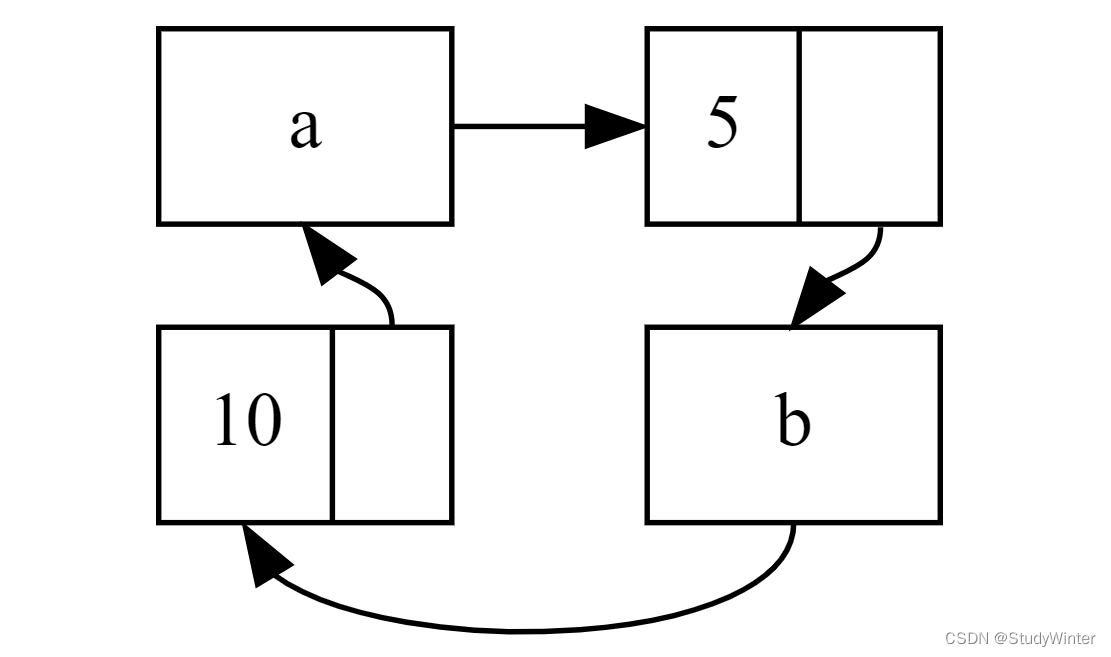
【Rust】Rust学习 第十五章智能指针
指针 (pointer)是一个包含内存地址的变量的通用概念。这个地址引用,或 “指向”(points at)一些其他数据。Rust 中最常见的指针是第四章介绍的 引用(reference)。引用以 & 符号为标志并借用…...

炒股怎样加杠杆?关于股票杠杠平台比例的选择知识分析
在股票市场中,加杠杆是一种常见的投资策略,可以帮助投资者提升收益,但也伴随着更高的风险。本文将介绍炒股加杠杆的具体步骤和股票杠杆平台比例选择的知识分析,帮助读者更好地了解并使用这一策略。 一、炒股加杠杆的步骤 1. 选择…...
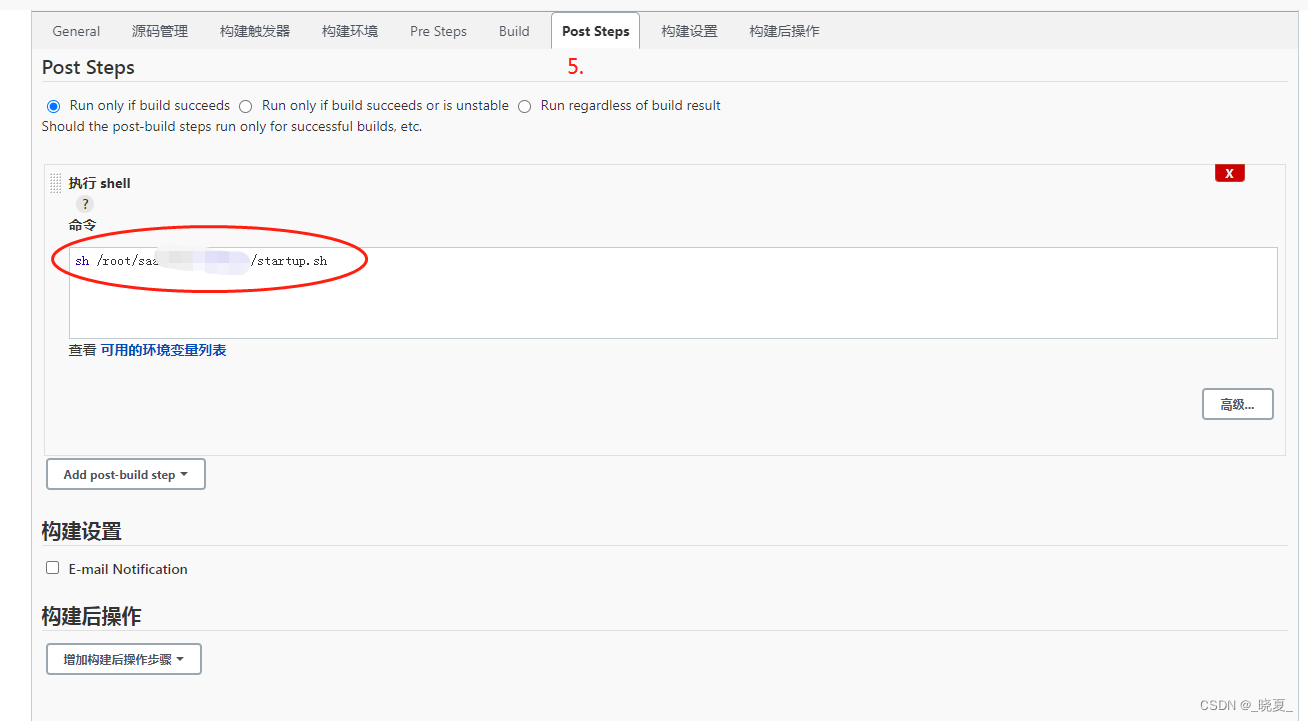
【jenkins】jenkins流水线构建打包jar,生成docker镜像,重启docker服务的过程,在jenkins上一键完成,实现提交代码自动构建的功能
【jenkins】jenkins流水线构建打包jar,生成docker镜像,重启docker服务的过程,在jenkins上一键完成,实现提交代码自动构建,服务重启,服务发布的功能。一键实现。非常的舒服。 1. 启动脚本 shell脚本 这是 s…...

Pytest使用fixture实现token共享
同学们在做pytest接口自动化时,会遇到一个场景就是不同的测试用例需要有一个登录的前置步骤,登录完成后会获取到token,用于之后的代码中。首先我先演示一个常规的做法。 首先在conftest定义一个login的方法,方法返回token pytes…...

You have docker-compose v1 installed, but we require Docker Compose v2.
curl -SL https://github.com/docker/compose/releases/download/v2.2.3/docker-compose-linux-x86_64 -o /usr/local/bin/docker-compose chmod x /usr/local/bin/docker-compose docker-compose --version...

nlopt在windows上的安装使用
nlopt在windows上的安装使用 目录 nlopt在windows上的安装使用一、nlopt下载二、def转lib三、代码 一、nlopt下载 1.下载nlopt库:https://nlopt.readthedocs.io/en/latest/ 2.解压 3.下载dll和def:http://ab-initio.mit.edu/wiki/index.php?titleNLopt…...

【React学习】React中的setState方法
1. setState概述 setState 是React框架中,用于更新组件状态的方法。 setState 方法由React组件继承自 React.Component 类的一部分。通过调用 setState,可以告诉 React要更新组件的状态,并触发组件的重新渲染。 this.setState(newState, ca…...
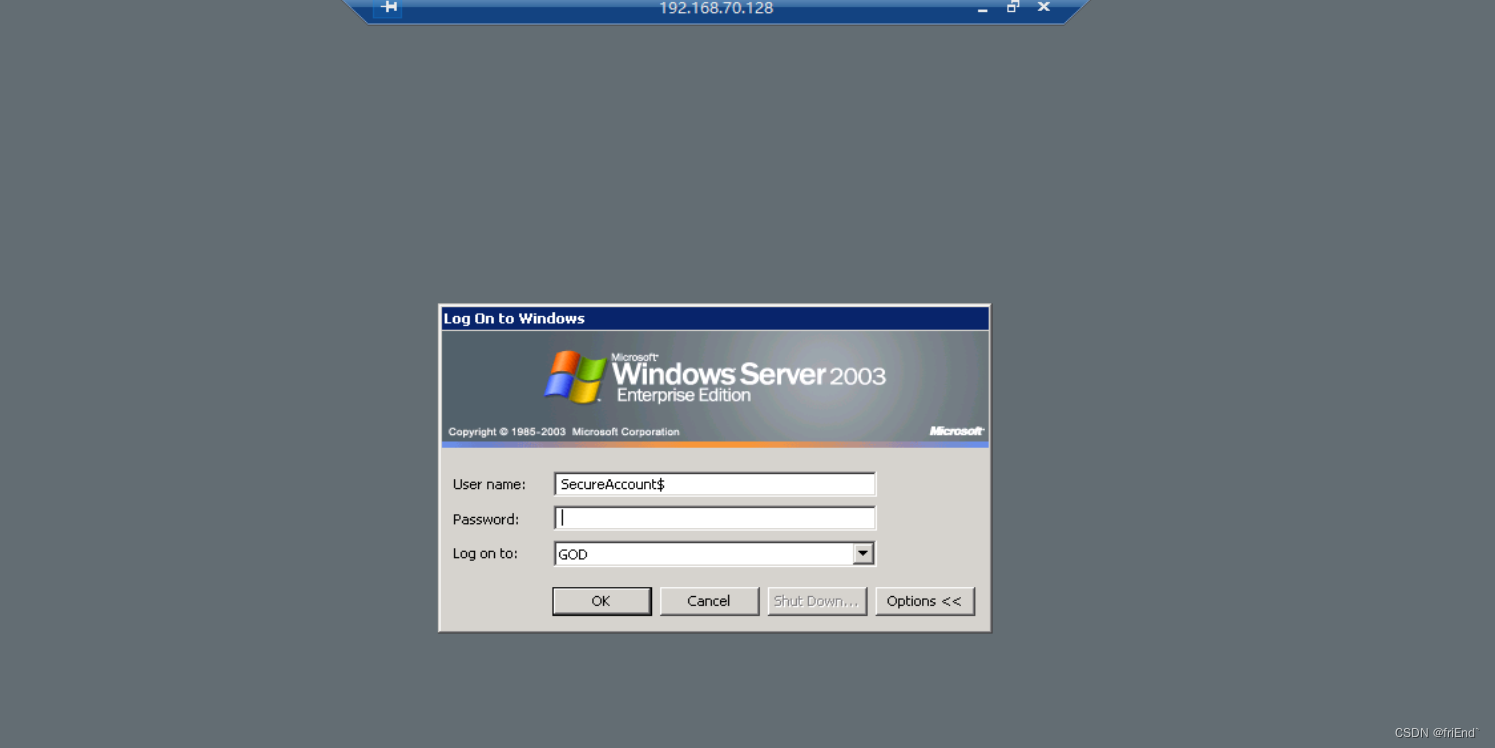
ATTCK实战系列——红队实战(一)
目录 搭建环境问题 靶场环境 web 渗透 登录 phpmyadmin 应用 探测版本 写日志获得 webshell 写入哥斯拉 webshell 上线到 msf 内网信息收集 主机发现 流量转发 端口扫描 开启 socks 代理 服务探测 getshell 内网主机 浏览器配置 socks 代理 21 ftp 6002/700…...
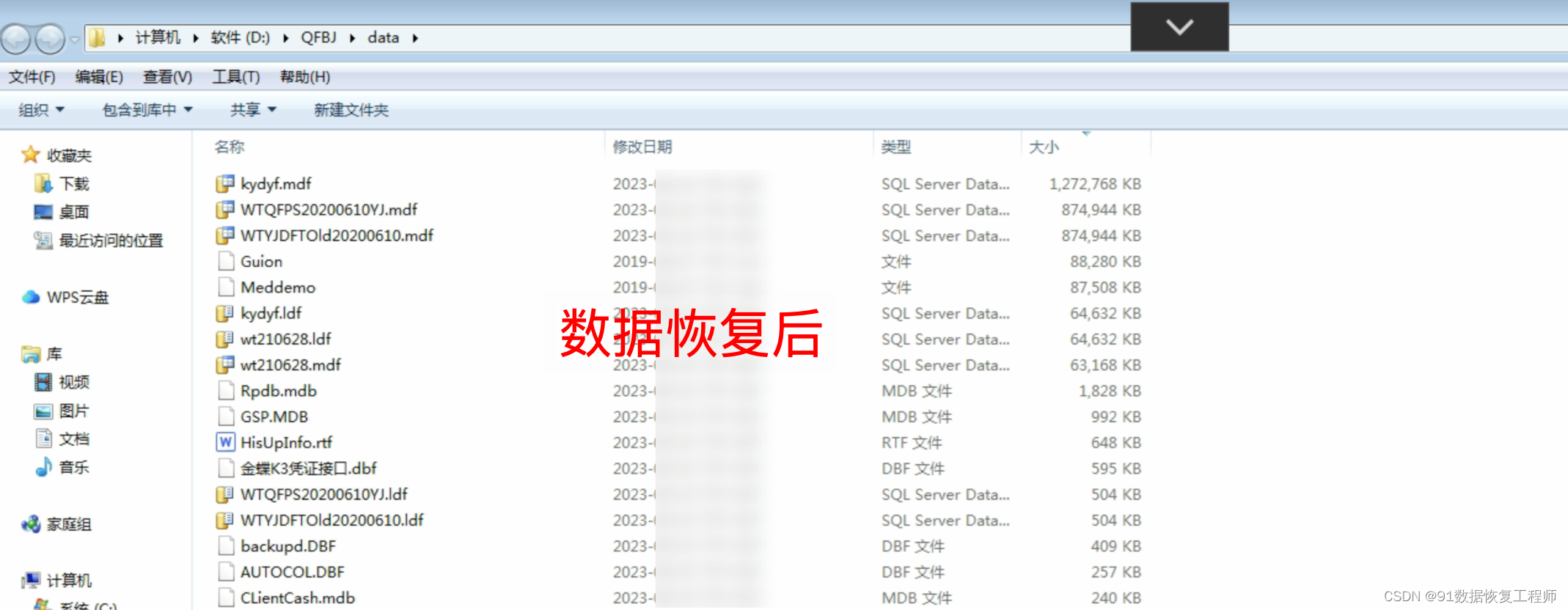
服务器感染了.360勒索病毒,如何确保数据文件完整恢复?
引言: 随着科技的不断进步,互联网的普及以及数字化生活的发展,网络安全问题也逐渐成为一个全球性的难题。其中,勒索病毒作为一种危害性极高的恶意软件,在近年来频频袭扰用户。本文91数据恢复将重点介绍 360 勒索病毒&a…...
【idea】社区版idea运行Tomcat
使用 Smart Tomcat插件 配置运行:...

网络安全面试题整理
目录标题 1.你常用的渗透工具有哪些?2.xss盲打到内网服务器的利用3.鱼叉式攻击和水坑攻击是什么?4.什么是虚拟机逃逸?5.中间人攻击的原理和防御?6.TCP三次握手过程?7.七层模型有哪七层?8.对云安全的理解&am…...

docker使用code-server搭建开发环境 v2.0
安装docker docker安装 下载安装nodejs、rust等环境 1、设置安装目录 # 创建路径 mkdir /usr/local/node # 切换路径 cd /usr/local/node2、安装nodejs16 # 下载 wget https://nodejs.org/dist/latest-v18.x/node-v18.17.1-linux-x64.tar.xz#解压 tar -xvf node-v18.17.1…...

Python写一个创意五子棋游戏
前言 在本教程中,我们将使用Python写一个创意五子棋游戏 📝个人主页→数据挖掘博主ZTLJQ的主页 个人推荐python学习系列: ☄️爬虫JS逆向系列专栏 - 爬虫逆向教学 ☄️python系列专栏 - 从零开始学python 首先 GomokuGame 类的构造函数 __ini…...
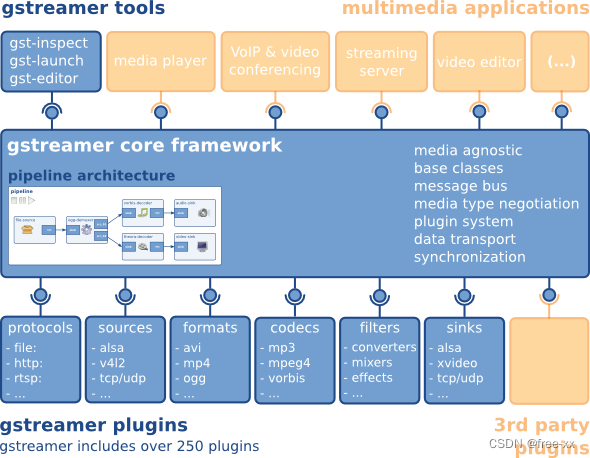
Nvidia Jetson 编解码开发(1)介绍
前言 由于项目需要,需要开发Jetson平台的硬件编解码; 优化CPU带宽,后续主要以介绍硬件编解码为主 1.Jetson各平台编解码性能说明 如下是拿了Jetson nano/tx2/Xavier等几个平台做对比; 这里说明的编解码性能主要是对硬件来说的…...

【操作系统】24王道考研笔记——第一章 计算机系统概述
第一章 计算机系统概述 一、操作系统基本概念 1.1 定义 1.2 特征 并发 (并行:指两个或多个事件在同一时刻同时发生) 共享 (并发性指计算机系统中同时存在中多个运行着的程序,共享性指系统中的资源可供内存中多个并…...
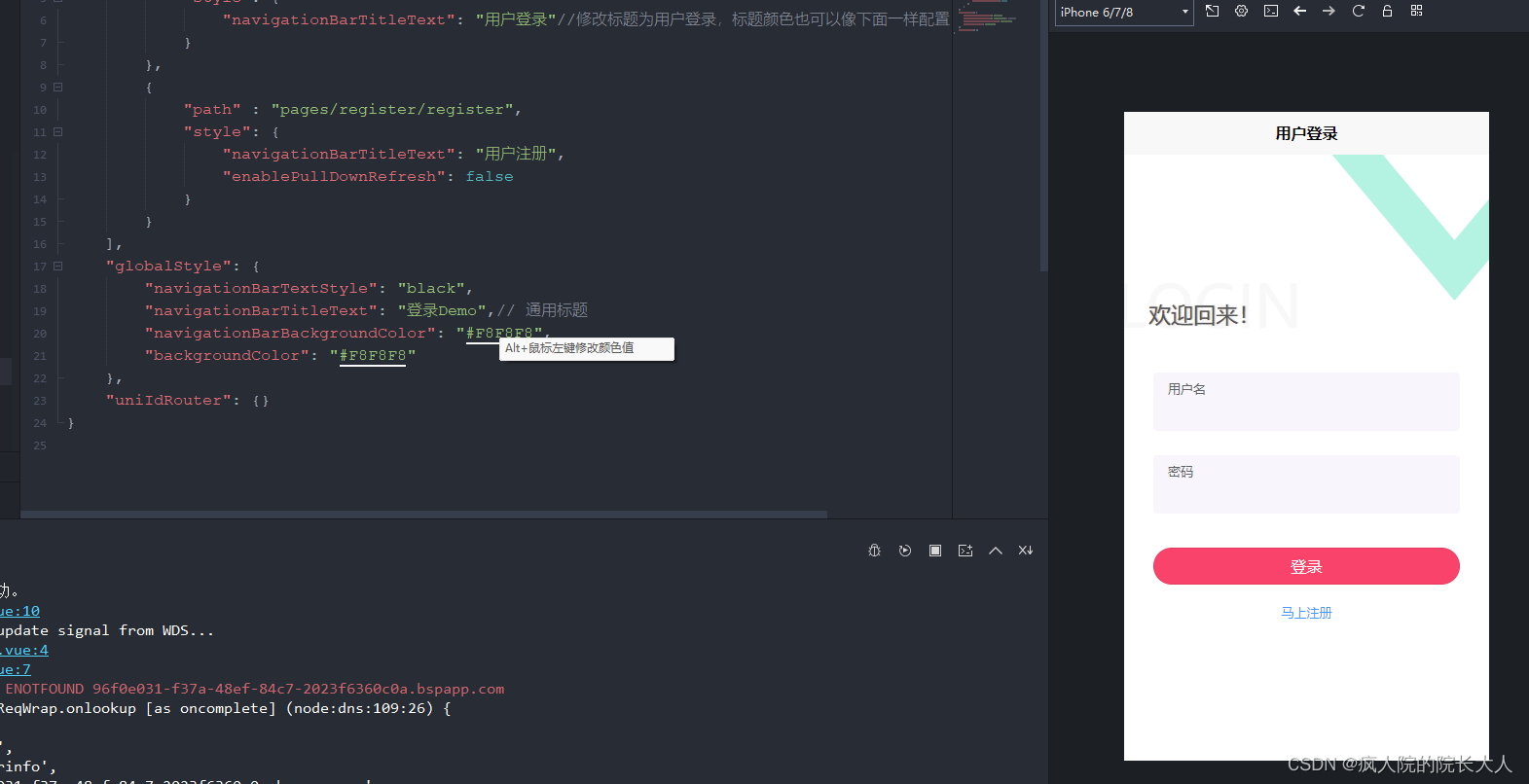
菜鸟Vue教程 - 实现带国际化的注册登陆页面
初接触vue的时候觉得vue好难,因为项目中要用到,就硬着头皮上,慢慢的发现也不难,无外乎画个布局,然后通过样式调整界面。在通过属性和方法跟js交互。js就和我们写的java代码差不多了,复杂一点的就是引用这种…...

Mybatis ORDER BY 排序失效 ORDER BY 与 CASE WHEN THEN 排序问题
一、ORDER BY 排序失效 如果传递给 mapper 的参数值是以 #{test_参数} 的形式,那么就会报错 具体如下: 传递参数是 name 排序规则是升序 asc package com.ruoyi.web.mapper; public interface TestMapper {List<TestEntity> getTestData( Para…...
日常BUG——微信小程序提交代码报错
😜作 者:是江迪呀✒️本文关键词:日常BUG、BUG、问题分析☀️每日 一言 :存在错误说明你在进步! 一、问题描述 在使用微信小程序开发工具进行提交代码时,报出如下错误: Invalid a…...

1048:有一门课不及格的学生
【题目描述】 给出一名学生的语文和数学成绩,判断他是否恰好有一门课不及格(成绩小于60分)。若该生恰好有一门课不及格,输出1;否则输出0。 【输入】 一行,包含两个在0到100之间的整数,分别是该生的语文成绩和数学成…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
