【数据结构】二叉树的链式结构的实现 -- 详解
一、前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习。
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 动态申请一个新节点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}注意:上述代码并不是创建二叉树的方式。
二、构建二叉树
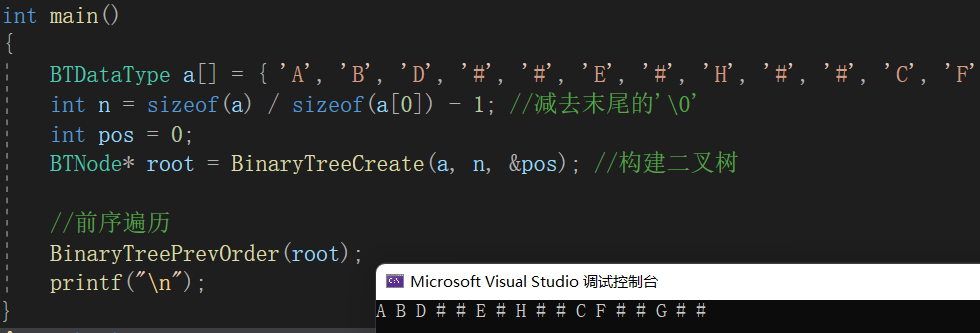
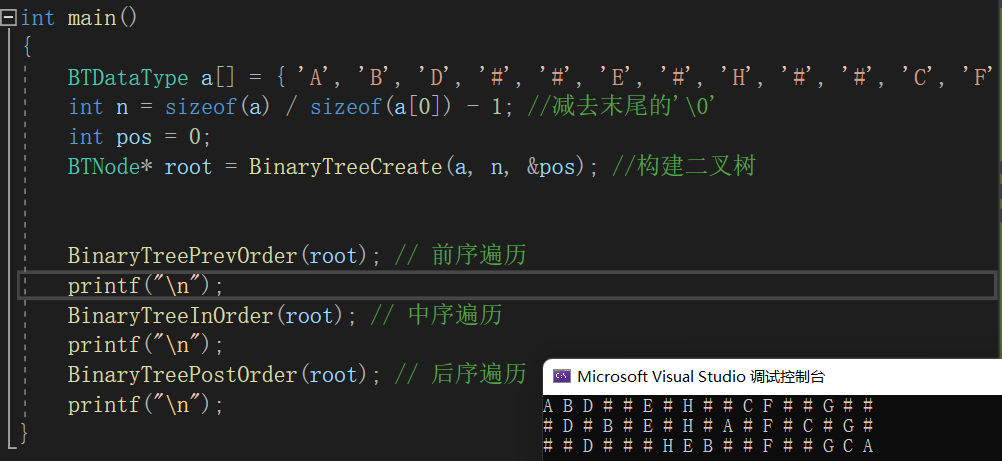
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n){return NULL;}char ch = a[*pi];(*pi)++;if (ch == '#'){return NULL;}BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));newNode->data = ch;newNode->left = BinaryTreeCreate(a, n, pi);newNode->right = BinaryTreeCreate(a, n, pi);return newNode;
}
三、二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历 (Traversal) 是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
二叉树的遍历方式主要有四种,先介绍三种,最后再介绍第四种。(利用了分治的思想)
- 前序遍历 (Preorder Traversal 亦称先序遍历),方式为先遍历根结点,左子树,右子树。
- 中序遍历 (Inorder Traversal),方式为先遍历左子树,根结点,右子树。
- 后序遍历 (Postorder Traversal),方式为先遍历左子树,右子树,根结点。
// 二叉树前序遍历 void PreOrder(BTNode* root); // 二叉树中序遍历 void InOrder(BTNode* root); // 二叉树后序遍历 void PostOrder(BTNode* root);
其中这三种遍历方式一般都用递归进行实现。
由于被访问的结点必是某子树的根,所以 N(Node)、L(Left subtree)和 R(Right subtree)又可解释为 根、根的左子树和根的右子树。NLR、LNR 和 LRN分别又称为先根遍历、中根遍历和后根遍历。注意 :1️⃣ 深度优先遍厉:前序遍厉、中序遍厉、后序遍厉,注意有些说法只认同前序遍厉。
2️⃣ 广度优先遍厉:层序遍厉。
1、前序遍历
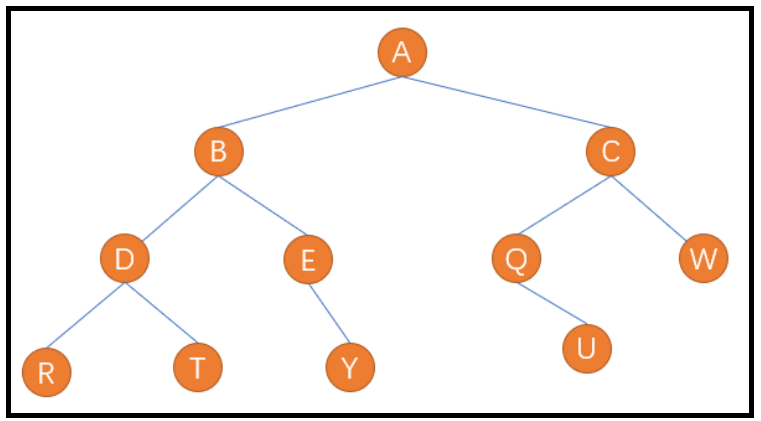
按照前序遍历的方式,我们应该先遍历根结点 A,然后再去遍历左子树。当进入左子树后,我们需要再执行前序遍历方式,即遍历 A 的左子树中的根结点 B,然后再遍历 B 的左子树。当我们再进入左子树,又是先遍历根结点D,然后又遍历左子树,按照顺序遍历到 R,此时终于完成根结点,左子树,接下来遍历右子树。进入右子树后,又遍历根结点T... ...,所以这种遍历方式属于递归性质的。(遍历顺序为:A–>B–>D–>R–>T–>E–>Y–>C–>Q–>U–>W)
// 二叉树前序遍历 void BinaryTreePrevOrder(BTNode* root) // 根->左子树->右子树 {if (root == NULL){printf("# "); // 用#代表NULLreturn;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right); }
【递归图解】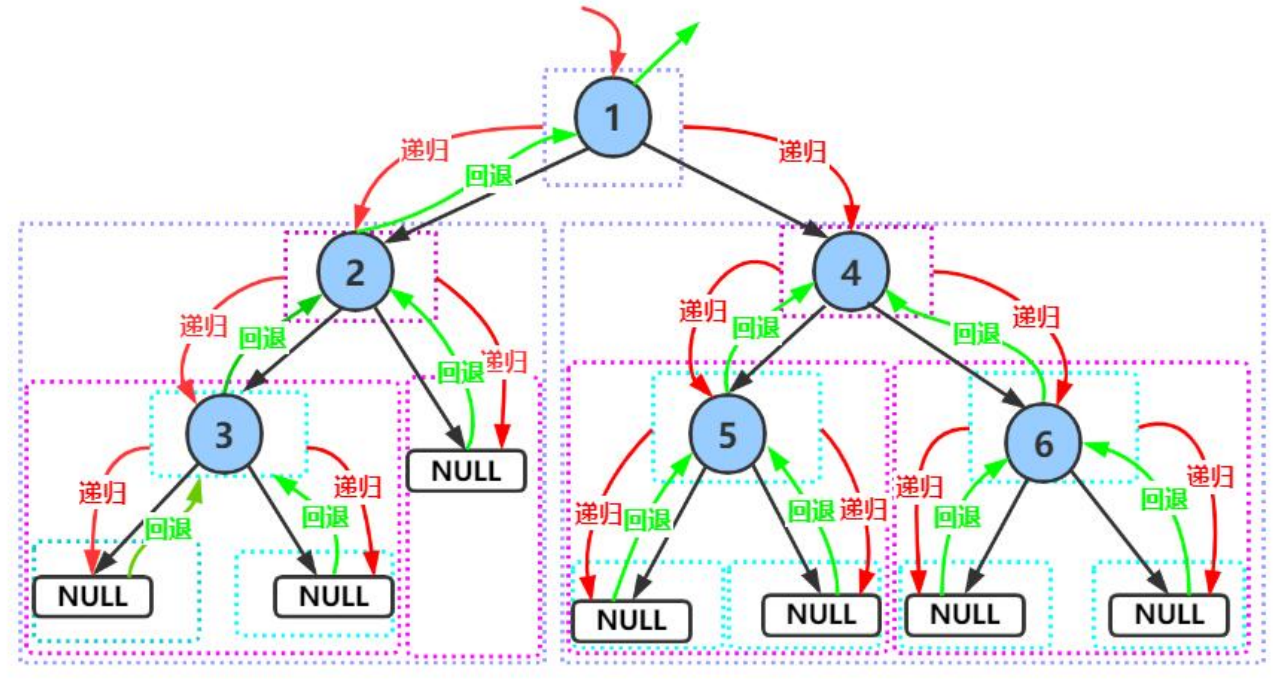
2、中序遍历
中序遍历方式为左子树,根结点,右子树。仍以上面的图为例,遍历顺序为:
R–>D–>T–>B–>E–>Y–>A–>Q–>U–>C–>W
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)// 左子树->根->右子树
{if (root == NULL){printf("# ");return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}3、后序遍历
后序遍历方式为 左子树,右子树,根结点。仍以上面的图为例,遍历顺序应该为:
R–>T–>D–>Y–>E–>B–>U–>Q–>W–>C–>A
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) // 左子树->右子树->根
{if (root == NULL){printf("# ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}【总结】
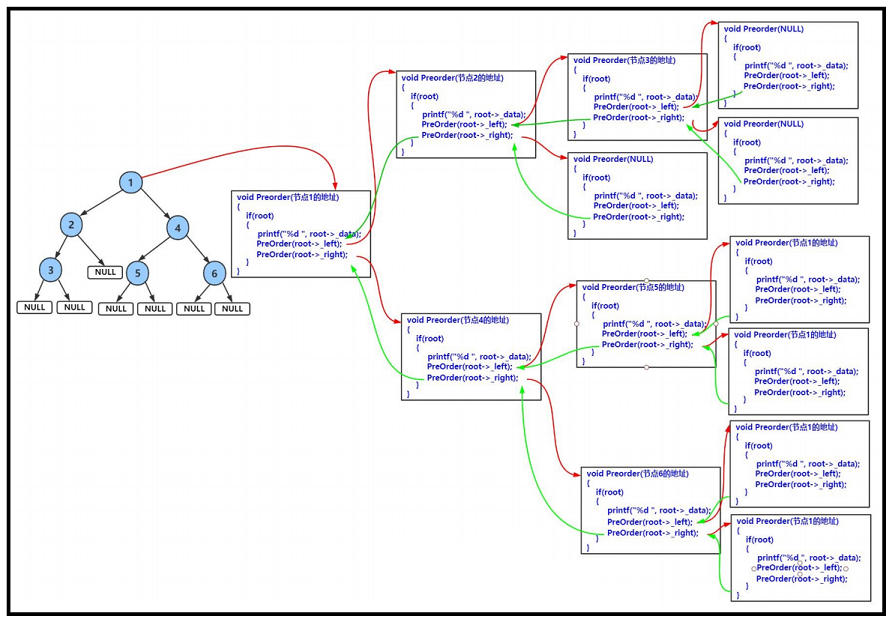
- 前序遍历结果:1->2->3->4->5->6
- 中序遍历结果:3->2->1->5->4->6
- 后序遍历结果:3->2->5->6->4->1
4、层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为 1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第 2 层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
// 层序遍历 void LevelOrder(BTNode* root);
注意:层序遍历一般需要使用队列。 (队列内容前面已经详细介绍过了)
【思路】先让根入队列,然后再让根出队列,当左子树不为 NULL 时让左子树入队列,当右子树不为NULL时让右子树入队列,然后不断地迭代下去,直至队列为空。记得出队列前要保存当前值来访问到该元素,Pop 到队列当中的值是地址,通过该地址来访问其中的 data。
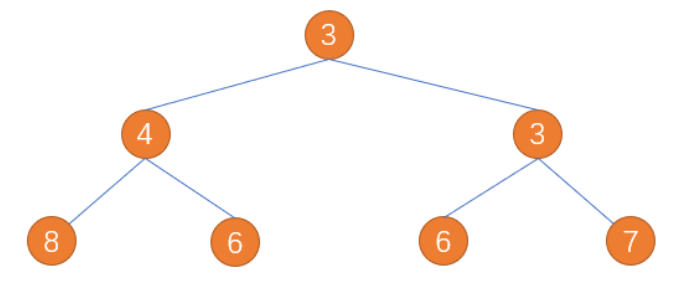
层序遍历结果为: 3->4->3->8->6->6->7
我们该如何利用队列实现呢?
- 判断当前队列是否为空。
- 队列为空:结束;队列非空:取出队列第一个元素入队列。
- 上一层出来后,再入下一层(即它的左右孩子节点)。
由于前面已经对队列的各种操作进行了详解,这里就不展开讲了。(直接运用之前写的 Queue.c 和 Queue.h)
// 层序遍历
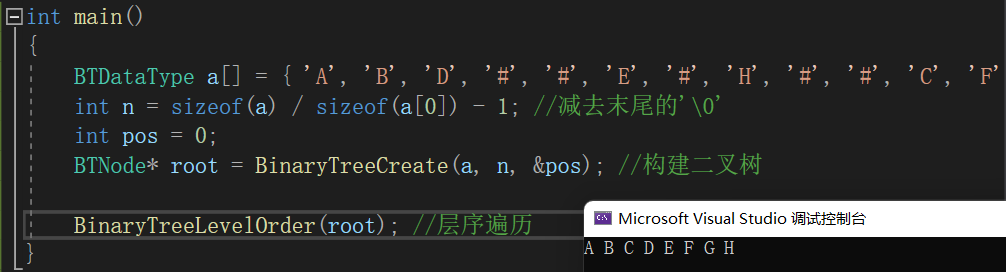
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素printf("%c ", front->data); // 打印节点值QueuePop(&q); // 出队列// 如果当前树根的左右孩子不为空 则分别入队列if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
四、二叉树其它接口的实现
1、二叉树的节点个数
按照递归的思想,计算二叉树的节点数量,我们可以认为 二叉树的节点个数 = 左子树数量 + 右子树数量 + 1,其中 1 是当前根节点数量(前提条件是存在根节点)。
⚪【思想 1】
迭代,使用栈来模拟递归的过程,用全局变量 / 静态局部变量来记录节点个数,遍历二叉树的所有节点,并累加节点的个数。
⚪【思想 2】
递归,利用分治的思想,函数使用带返回值的方式,其内部的递归本质上是一个后序遍厉(左子树->右子树->根节点)。
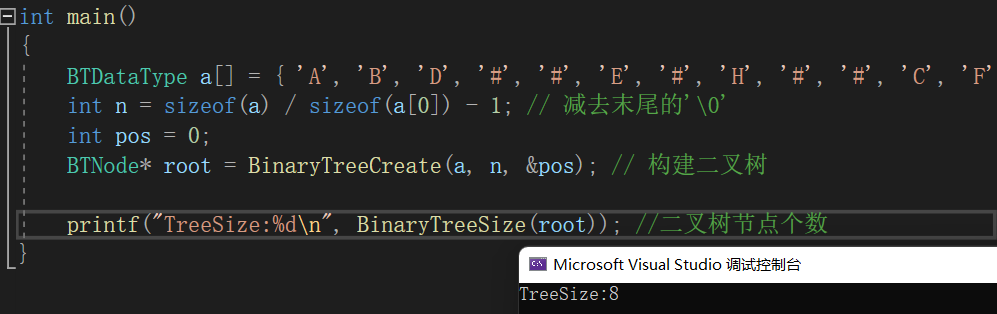
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
2、二叉树叶子节点个数
按照递归的思想,计算二叉树的叶子节点数量,我们可以认为 叶子节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数 + 0,0 是因为当前根结点有子树,说明根结点不是叶子结点。
⚪【思想】
以 left 和 right 为标志,如果都为 NULL,则说明该节点是叶子节点。
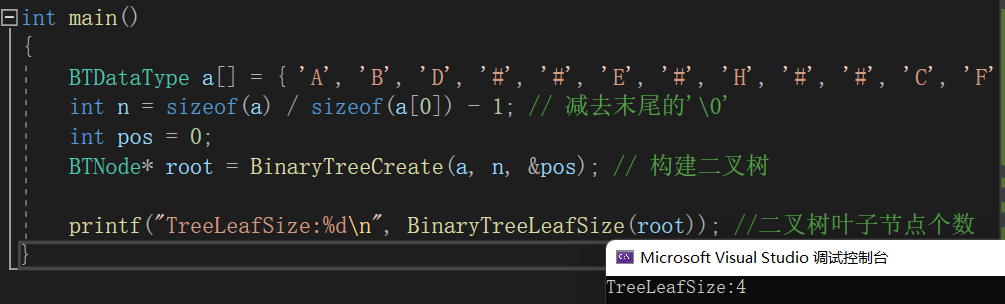
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{// 先判断当前访问的节点是否为空if (root == NULL) {return 0;}// 当前节点不为空,它的左右孩子都为空,说明该节点是叶子节点if (root->left == NULL && root->right == NULL){return 1;}// 当前节点不为空,左右孩子不都为空,则继续往下遍历return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
3、二叉树第k层节点个数
⚪【思想】
求当前树的第 k 层节点个数 = 左子树的第 k-1 层节点个数 + 右子树的第 k-1 层节点个数 (当 k=1 时,说明此层就是目标层)
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k >= 1);if (root == NULL) // 先判断当前访问的节点是否为空{return 0;}if (k == 1) // 当前节点不为空,而k已经减到1了,说明遍历到了第k层,说明该节点是第k层的{return 1;}// 还没有遍历到第k层,我们就继续往下遍历return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}如何知道这个节点是不是第 k 层的?
求二叉树第 k 层的节点个数,我们从根节点开始往下遍历(按根->左->右的顺序),每遍历一次 k 就减 1一次,当 k==1 时,说明我们遍历到了第 k 层,此时访问该层的节点。如果它不为空,则二叉树第 k 层的节点个数就要 +1。
4、二叉树查找值为x的节点
⚪【思想】
按照递归思想,先判断当前结点是否是目标节点,然后查找左子树,再查找右子树。
如果左右子树都没有找到,就返回NULL。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL) // 先判断当前访问的节点是否为空{return NULL;}if (root->data == x) // 判断要找的x值节点是不是当前节点{return root;}// 不是当前节点,则继续去该节点的左子树中找BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1){return ret1;}// 还没找到,再继续去该节点的右子树中找BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2){return ret2;}return NULL; // 当前节点及其左右子树中都没找到,返回NULL
}5、销毁二叉树
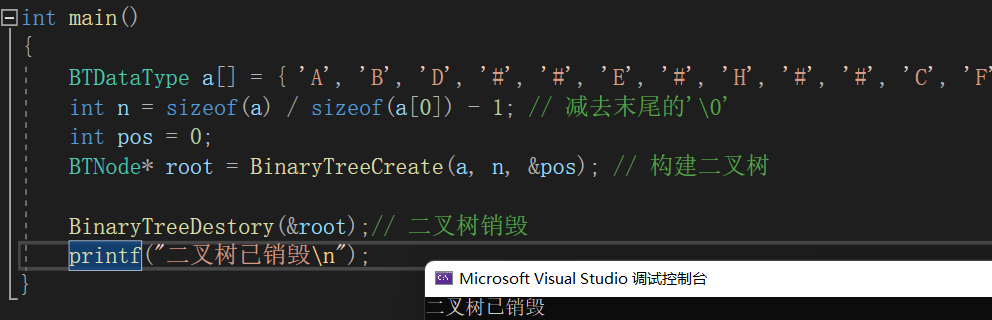
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{// 如果使用前中序遍历销毁,节点会先被销毁,变成随机值,就不知道它的左右子树位置了 所以采用后序遍历销毁if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL; // 将根节点设置为NULL 防止野指针
}
注意:如果这里使用前序遍历或中序遍历进行销毁,节点会先被销毁,变成随机值,就不知道它的左右子树位置了,所以应该采用后序遍历来销毁二叉树。
如果这里传进来的是一级指针,由于要在函数内改变形参的值,无法改变外部实参的值,所以我们需要在函数外置头节点指针为NULL。
6、判断二叉树是否是完全二叉树
⚪【思想】
层序遍历时,把空节点也入队列。
- 完全二叉树中,非空节点是连续的,则空节点是连续的。
- 非完全二叉树中,非空节点不是连续的,则空节点不是连续的。
所以在出队时,判断一下,出到第一个空节点时,跳出循环;
在下面重新写一个循环继续出队,并检查出队元素:
- 如果第一个空节点后面的全是空节点,说明是完全二叉树。
- 如果第一个空节点后面的有非空节点,说明是非完全二叉树。
// 判断二叉树是否是完全二叉树(利用层序遍历的思想来判断)
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素QueuePop(&q); //出队列if (front){// 不管当前树根的左右孩子是否为空,都分别入队列QueuePush(&q, front->left);QueuePush(&q, front->right);}else{break; //遇到空后,跳出层序遍历}}// 如果后面全是空,则是完全二叉树,否则不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true; // 出队的节点中,如果没有出现非空节点,说明是完全二叉树出队的节点中,如果没有出现非空节点,说明是完全二叉树
}
五、代码整合
1、Queue.h
// Queue.h
#pragma once#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>struct BinaryTreeNode;typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;
}Queue;void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);2、Queue.c
// Queue.c
#define _CRT_SECURE_NO_WARNINGS 1#include "Queue.h"void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));newnode->data = x;newnode->next = NULL;if (pq->head == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));QNode* next = pq->head->next;free(pq->head);pq->head = next;if (pq->head == NULL){pq->tail = NULL;}
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}int QueueSize(Queue* pq)
{assert(pq);int n = 0;QNode* cur = pq->head;while (cur){++n;cur = cur->next;}return n;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL;
}3、test.c
// test.c
#define _CRT_SECURE_NO_WARNINGS 1#include "Queue.h"typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//动态申请一个新节点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n){return NULL;}char ch = a[*pi];(*pi)++;if (ch == '#'){return NULL;}BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));newNode->data = ch;newNode->left = BinaryTreeCreate(a, n, pi);newNode->right = BinaryTreeCreate(a, n, pi);return newNode;
}// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{// 先判断当前访问的节点是否为空if (root == NULL) {return 0;}// 当前节点不为空,它的左右孩子都为空,说明该节点是叶子节点if (root->left == NULL && root->right == NULL){return 1;}// 当前节点不为空,左右孩子不都为空,则继续往下遍历return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k >= 1);if (root == NULL) // 先判断当前访问的节点是否为空{return 0;}if (k == 1) // 当前节点不为空,而k已经减到1了,说明遍历到了第k层,说明该节点是第k层的{return 1;}// 还没有遍历到第k层,我们就继续往下遍历return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL) // 先判断当前访问的节点是否为空{return NULL;}if (root->data == x) // 判断要找的x值节点是不是当前节点{return root;}// 不是当前节点,则继续去该节点的左子树中找BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1){return ret1;}// 还没找到,再继续去该节点的右子树中找BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2){return ret2;}return NULL; // 当前节点及其左右子树中都没找到,返回NULL
}// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{// 如果使用前中序遍历销毁,节点会先被销毁,变成随机值,就不知道它的左右子树位置了 所以采用后序遍历销毁if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL; // 将根节点设置为NULL 防止野指针
}// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root) // 根->左子树->右子树
{if (root == NULL){printf("# "); // 用#代表NULLreturn;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)// 左子树->根->右子树
{if (root == NULL){printf("# ");return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) // 左子树->右子树->根
{if (root == NULL){printf("# ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素printf("%c ", front->data); // 打印节点值QueuePop(&q); // 出队列// 如果当前树根的左右孩子不为空 则分别入队列if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}// 判断二叉树是否是完全二叉树(利用层序遍历的思想来判断)
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root) // 树的根节点root不为空 将根节点入队列{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 获取队列头部元素QueuePop(&q); //出队列if (front){// 不管当前树根的左右孩子是否为空,都分别入队列QueuePush(&q, front->left);QueuePush(&q, front->right);}else{break; //遇到空后,跳出层序遍历}}// 如果后面全是空,则是完全二叉树,否则不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true; // 出队的节点中,如果没有出现非空节点,说明是完全二叉树出队的节点中,如果没有出现非空节点,说明是完全二叉树
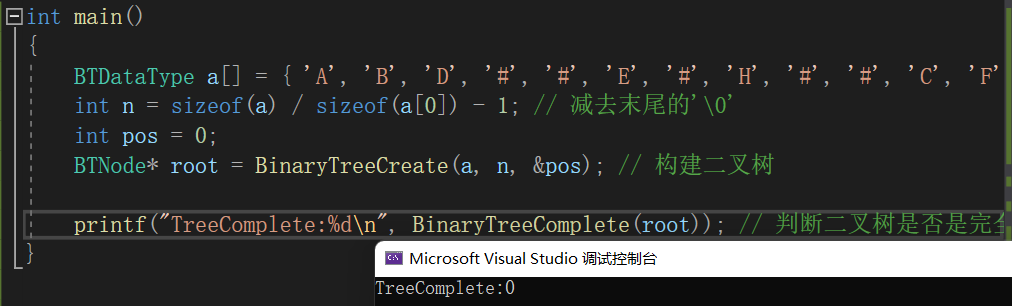
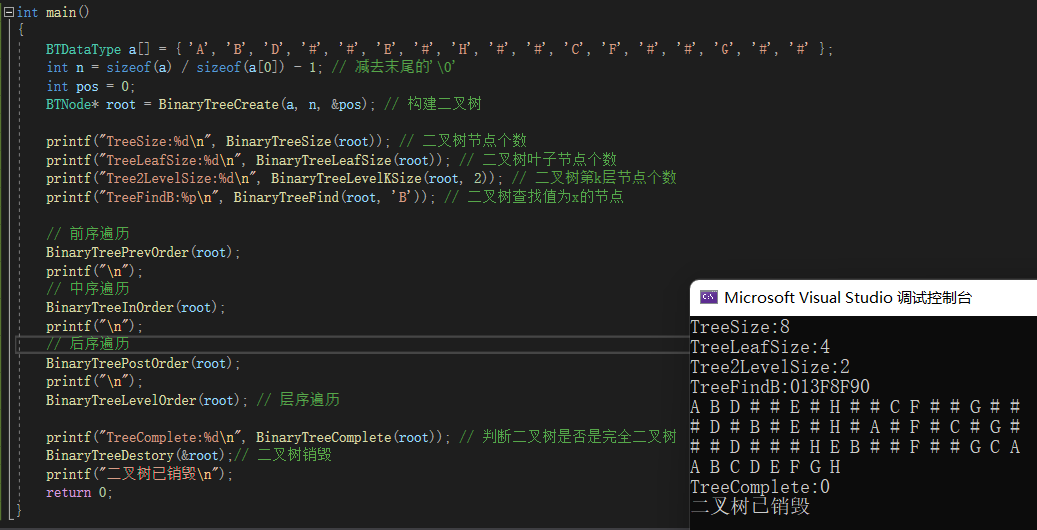
}int main()
{BTDataType a[] = { 'A', 'B', 'D', '#', '#', 'E', '#', 'H', '#', '#', 'C', 'F', '#', '#', 'G', '#', '#' };int n = sizeof(a) / sizeof(a[0]) - 1; // 减去末尾的'\0'int pos = 0;BTNode* root = BinaryTreeCreate(a, n, &pos); // 构建二叉树printf("TreeSize:%d\n", BinaryTreeSize(root)); // 二叉树节点个数printf("TreeLeafSize:%d\n", BinaryTreeLeafSize(root)); // 二叉树叶子节点个数printf("Tree2LevelSize:%d\n", BinaryTreeLevelKSize(root, 2)); // 二叉树第k层节点个数printf("TreeFindB:%p\n", BinaryTreeFind(root, 'B')); // 二叉树查找值为x的节点// 前序遍历BinaryTreePrevOrder(root);printf("\n");// 中序遍历BinaryTreeInOrder(root);printf("\n");// 后序遍历BinaryTreePostOrder(root);printf("\n");BinaryTreeLevelOrder(root); // 层序遍历printf("TreeComplete:%d\n", BinaryTreeComplete(root)); // 判断二叉树是否是完全二叉树BinaryTreeDestory(&root);// 二叉树销毁printf("二叉树已销毁\n");return 0;
}六、程序运行整体效果
相关文章:

【数据结构】二叉树的链式结构的实现 -- 详解
一、前置说明 在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习。 typedef char BTDataType;typedef struct Binar…...

【C语言】什么是结构体内存对齐?结构体的大小怎么计算?
目录 1.结构体内存对齐 对偏移量的理解: 2.结构体的大小计算 2.1结构体中只有普通的数据类型的大小计算 2.2 结构体中有嵌套的结构体的大小计算 3.修改默认对齐数 4.为什么存在内存对齐? 这篇文章主要介绍结构体内存对齐和如何计算大小。 在学习结构体内存…...

【Redis】Redis中的布隆过滤器
【Redis】Redis中的布隆过滤器 前言 在实际开发中,会遇到很多要判断一个元素是否在某个集合中的业务场景,类似于垃圾邮件的识别,恶意IP地址的访问,缓存穿透等情况。类似于缓存穿透这种情况,有许多的解决方法…...

接口测试 —— Jmeter 参数加密实现
Jmeter有两种方法可以实现算法加密 1、使用__digest自带函数 参数说明: Digest algorithm:算法摘要,可输入值:MD2、MD5、SHA-1、SHA-224、SHA-256、SHA-384、SHA-512 String to be hashed:要加密的数据 Salt to be…...

Linux c语言字节序
文章目录 一、简介二、大小端判断2.1 联合体2.2 指针2.3 网络字节序 一、简介 字节序(Byte Order)指的是在存储和表示多字节数据类型(如整数和浮点数)时,字节的排列顺序。常见的字节序有大端字节序(Big En…...

批量将excel中第5列中内容将人名和电话号码进行分列
使用Python可以使用openpyxl库来实现批量将Excel中第5列的内容分列为人名和电话号码的操作。下面是示例代码: import openpyxl def split_names_and_phone_numbers(file_path, sheet_name): # 加载Excel文件 workbook openpyxl.load_workbook(file_path) …...

WPF DataGrid columns表头根据数据集动态动态生成Demo
思路是这样的,数组集合装表头的信息,遍历这个集合,遍历过程中处理一下数据,然后就把每表头信息添加到dataGrid2.Columns.Add(templateColumn); 1,页面Xaml代码: <DataGrid x:Name"dataGrid" …...
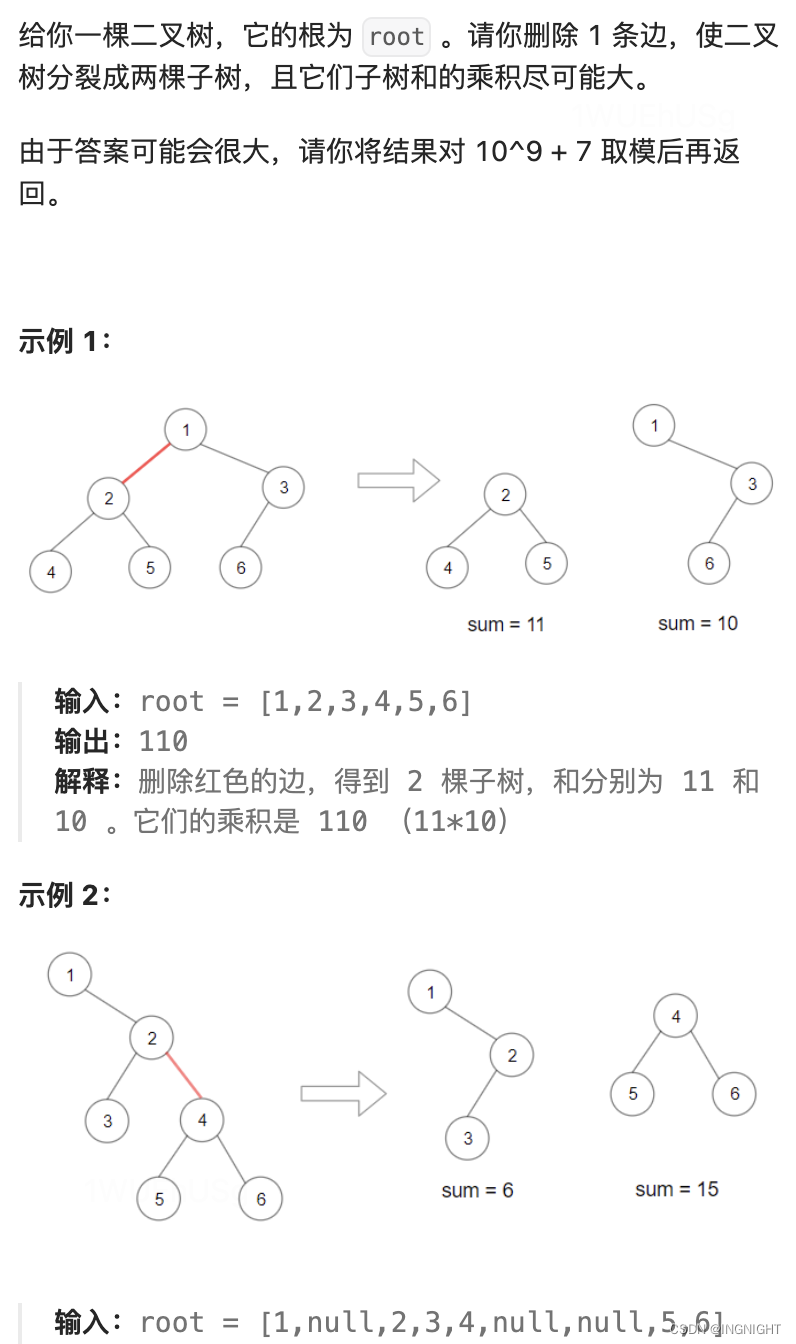
1339. 分裂二叉树的最大乘积
链接: 1339. 分裂二叉树的最大乘积 题解: /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* …...

【C++】Stack和Queue
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析3 目录 👉🏻Stack Constructor👉🏻Stack …...

Maven之tomcat7-maven-plugin 版本低的问题
tomcat7-maven-plugin 版本『低』的问题 相较于当前最新版的 tomcat 10 而言,tomcat7-maven-plugin 确实看起来很显老旧。但是,这个问题并不是问题,至少不是大问题。 原因 1:tomcat7-maven-plugin 仅用于我们(程序员&…...
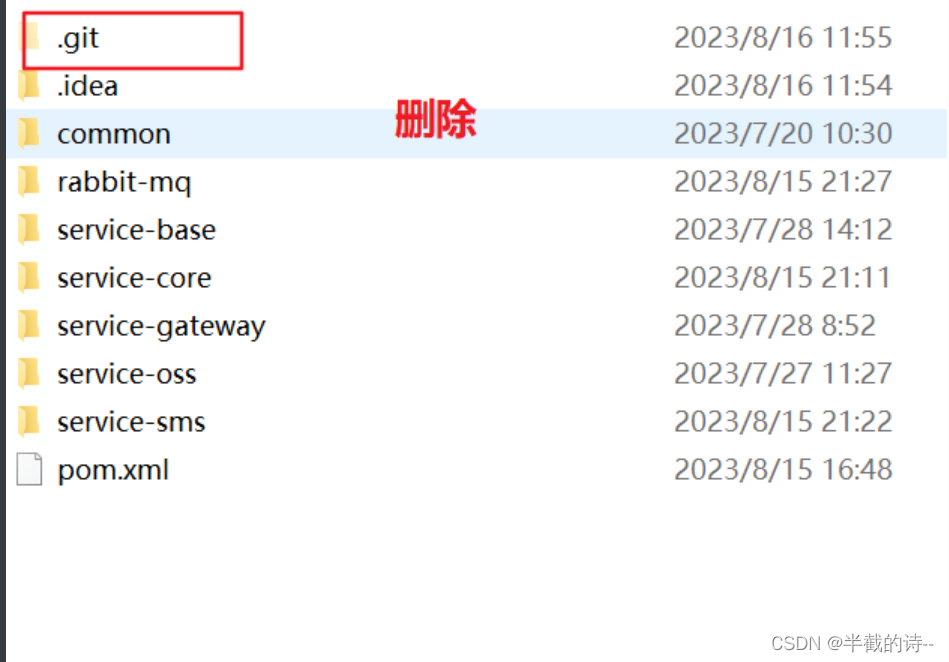
在项目中如何解除idea和Git的绑定
在项目中如何解除idea和Git的绑定 1、点击File--->Settings...(CtrlAltS)--->Version Control--->Directory Mappings--->点击取消Git的注册根路径: 2、回到idea界面就没有Git了: 3、给这个项目初始化 这样就可以重新绑定远程仓库了&#x…...
AGI 在网易云信的技术提效和业务创新
We believe our research will eventually lead to artificial general intelligence, a system that can solve human-level problems. Building safe and beneficial AGI is our mission. ---- OpenAI 通用人工智能 AGI 作为 AI 的终极形态,是 AI 行业内追求的演…...

线性代数的学习和整理9(草稿-----未完成)
3.3 特征值和特征向量是什么? 直接说现在:特征向量这个块往哪个方向进行了拉伸,各个方向拉伸了几倍。这也让人很容易理解为什么,行列式的值就是特征值的乘积。 特征向量也代表了一些良好的性质,即这些线在线性变换后…...

React的useReducer与Reudx对比
useReducer 和 Redux 都是用于处理应用程序的状态管理的工具,但它们在概念和使用场景上存在一些区别。 useReducer: useReducer 是 React 提供的一个 Hook,用于管理局部状态。它接受一个 reducer 函数和初始状态,并返回一个包含当…...
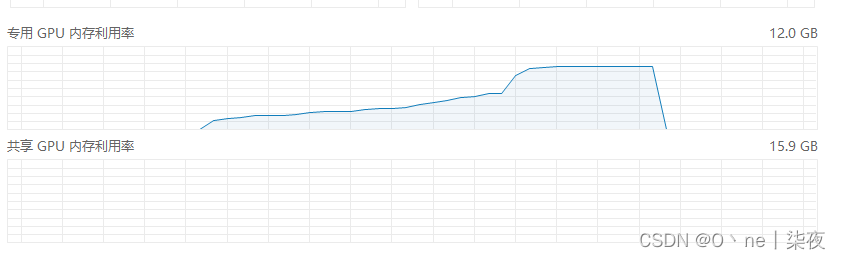
深度学习环境搭建 cuda、模型量化bitsandbytes安装教程 windows、linux
cuda、cudann、conda安装教程 输入以下命令,查看 GPU 支持的最高 CUDA 版本。 nvidia-smi cuda安装(cudatoolkit) 前往 Nvidia 的 CUDA 官网:CUDA Toolkit Archive | NVIDIA Developer CUDA Toolkit 11.8 Downloads | NVIDIA …...

pythond assert 0 <= colx < X12_MAX_COLS AssertionError
python使用xlrd读取excel时,报错: assert 0 < colx < X12_MAX_COLS AssertionError 大意是excel列太多了。主要是xlrd库的问题。最好的方法是不用它,但是我用的其他人提供的工具用到它,没法改。 尝试手动删除excel的列&am…...
js简介以及在html中的2种使用方式(hello world)
简介 javascript :是一个跨平台的脚本语言;是一种轻量级的编程语言。 JavaScript 是 Web 的编程语言。所有现代的 HTML 页面都使用 JavaScript。 HTML: 结构 css: 表现 JS: 行为 HTMLCSS 只能称之为静态网页࿰…...

vsCode使用cuda
一、vsCode使用cuda 前情提要:配置好mingw: 1.安装cuda 参考: **CUDA Toolkit安装教程(Windows):**https://blog.csdn.net/qq_42951560/article/details/116131410 2.在vscode中添加includePath c_cp…...

ubuntu无法使用apt命令时怎么安装库
如题 因为某些原因,不能直接联网使用apt命令安装库。只能手动去ubuntu镜像源里 找对应的包的deb安装文件 镜像源地址(适用于AMD64架构,就是常见的PC的X86-64啦) 镜像源地址(适用于ARM64,armhf,ppc64el,riscv64,s390x架构ÿ…...

防火墙firewall
一、什么是防火墙 二、iptables 1、iptables介绍 2、实验 138的已经被拒绝,1可以 三、firewalld 1、firewalld简介 关闭iptables,开启firewalld,curl不能使用,远程连接ssh可以使用 添加80端口 这样写也可以:添加http…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...