leetcode做题笔记90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
思路一:回溯
int comp(const void* a, const void* b) {return *(int*)a - *(int*)b;
}void backtracking(int* nums, int numsSize, int** res, int* returnSize, int** returnColumnSizes, int* path, int pathSize, int startIndex) {res[*returnSize] = (int*)malloc(sizeof(int) * pathSize);memcpy(res[*returnSize], path, sizeof(int) * pathSize);(*returnColumnSizes)[*returnSize] = pathSize;(*returnSize)++;for (int i = startIndex; i < numsSize; i++) {path[pathSize] = nums[i];backtracking(nums, numsSize, res, returnSize, returnColumnSizes, path, pathSize + 1, i + 1);while (i < numsSize - 1 && nums[i] == nums[i + 1]) i++; }
}int** subsetsWithDup(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){*returnSize = 0;*returnColumnSizes = (int*)malloc(sizeof(int) * 10001);int** res = (int**)malloc(sizeof(int*) * 10001);int* path = (int*)malloc(sizeof(int) * numsSize);qsort(nums, numsSize, sizeof(int), comp); backtracking(nums, numsSize, res, returnSize, returnColumnSizes, path, 0, 0);return res;
}分析:
本题与78子集问题很像,只需在78代码的基础上考虑数字重复问题即可,对于数字重复可先将数组内数组排序一遍再加上while (i < numsSize - 1 && nums[i] == nums[i + 1]) i++;这行代码即可解决
总结:
本题考察回溯的应用,考虑重复数字,对于nums[i] == nums[i + 1]直接跳过处理即可
相关文章:

leetcode做题笔记90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。 思路一:回溯 int comp(const void* a, cons…...
“开发和运维”只是一个开始,最终目标是构建高质量的软件工程
随着技术的飞速发展,软件行业不断寻求改进和创新的方法来提供更高质量的产品。在这方面,DevOps已经展现出了巨大的潜力。通过打破开发和运维之间的壁垒,DevOps将持续集成、持续交付和自动化流程引入到软件开发中,使团队能够更快地…...
自学C#,要懂得善用MSDN
很多初学者学习编程,都会通过看别人写的教程、或者录制的视频,来学习。 这是一个非常好的途径,因为这个是非常高效的。 但是这样,存在两个问题: 1、教程不够全面:任何再好的教程,都无法囊括所…...
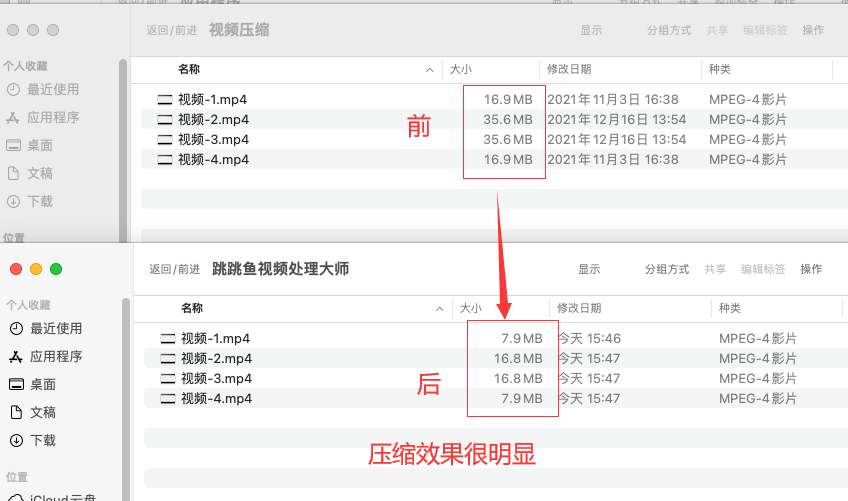
mac上如何压缩视频大小?
mac上如何压缩视频大小?由于视频文件体积庞大,常常会占据我们设备的大量存储空间。通常情况下,我们选择删除视频以释放内存,但这将永久丢失它们。然而,有一种更好的方法可以在不删除视频的情况下减小内存占用ÿ…...
git merge规则
参考文档:https://juejin.cn/post/7129333439299321887 丹尼尔:Hi,蛋兄,周杰伦都出新专辑了,你咋还不更新啊,真的打算半年一更啊? 蛋先生:好像确实是这样,要不࿰…...

【周末闲谈】关于“数据库”你又知道多少?
个人主页:【😊个人主页】 系列专栏:【❤️周末闲谈】 系列目录 ✨第一周 二进制VS三进制 ✨第二周 文心一言,模仿还是超越? ✨第二周 畅想AR 文章目录 系列目录前言数据库数据库的五大特点数据库介绍数据库管理系统&a…...

C++ 对象生成:构造函数
对象生成:构造函数 一、构造函数特性二、三种构造函数1.无参构造函数2.有参构造函数3.拷贝构造函数 一、构造函数特性 C编译器提供了构造函数供程序生成对象这是一个与类同名的函数,参数可以有多种形式(重载)没有返回类型声明一般…...

RFID如何在汽车混流生产中进行车辆跟踪?
在汽车混流生产中,RFID技术可以对每个车辆进行唯一标识,从而实现车辆生产全程跟踪。实时确定车辆的位置、状态和生产过程,生产管理系统就能够对生产流程进行实时监控和管理,及时发现和解决问题,提高生产效率和质量。 焊…...
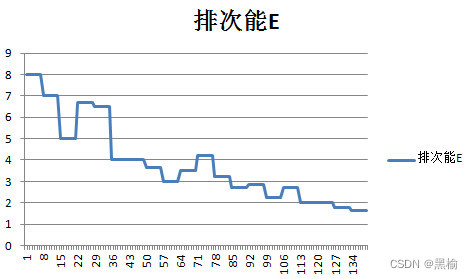
差值结构的复合底部
( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 让网络的输入只有3个节点,AB训练集各由6张二值化的图片组成,让A 中有3个点,B中有1个点,且不重合,统计迭代次数并排序。 其中有20组数据 让迭代次数与排斥能成反比,排…...

在Docker 上使用 Nginx 配置https及wss
预先创建挂载文件 /mydata/nginx/conf/nginx.conf /mydata/nginx/cert /mydata/nginx/conf.d /mydata/nginx/html /mydata/nginx/logs运行并且挂载容器 docker run -p 80:80 -p 443:443 --name nginx01 --restartalways \ -v /mydata/nginx/conf/nginx.conf:/etc/nginx/ngi…...

git回退操作
1. 在工作区回退: 此时文件没有经过任何提交 git checkout -- filename2. git add之后回退 git reset HEAD3. git commit 之后回退 git reset --hard commit_id(前4位)其中,commit_id可通过git log查看,例如: qzcryqz MINGW6…...

C++系列-类和对象-静态成员
类和对象-静态成员 静态成员静态成员变量静态成员函数 静态成员 静态成员就是在成员变量或者是成员函数前面加上static关键字。 静态成员变量 所有对象共享同一份数据在编译阶段分配内存类内声明,类外初始化可以通过对象或者类名进行访问。静态成员变量也具有访问…...
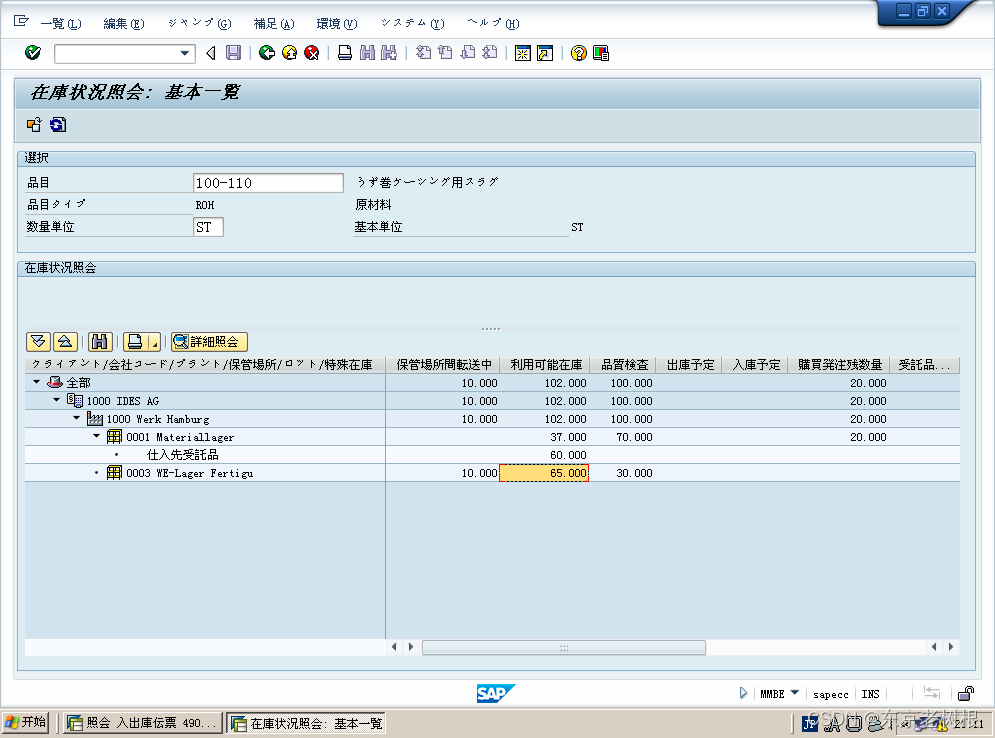
SAP MM学习笔记26- SAP中 振替转记(转移过账)和 在库转送(库存转储)2- 品目Code振替转记 和 在库转送
SAP 中在库移动 不仅有入库(GR),出库(GI),也可以是单纯内部的转记或转送。 1,振替转记(转移过账) 2,在库转送(库存转储) 1ÿ…...

【Python机器学习】实验13 基于神经网络的回归-分类实验
文章目录 神经网络例1 基于神经网络的回归(简单例子)1.1 导入包1.2 构造数据集(随机构造的)1.3 构造训练集和测试集1.4 构建神经网络模型1.5 采用训练数据来训练神经网络模型 实验:基于神经网络的分类(鸢尾花数据集)1. 导入包2. 构造数据集3.…...
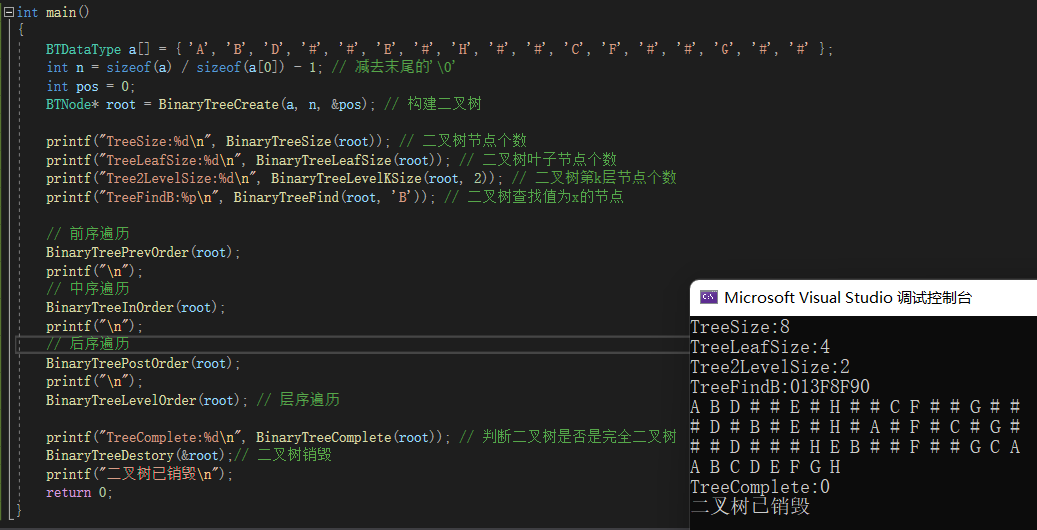
【数据结构】二叉树的链式结构的实现 -- 详解
一、前置说明 在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习。 typedef char BTDataType;typedef struct Binar…...

【C语言】什么是结构体内存对齐?结构体的大小怎么计算?
目录 1.结构体内存对齐 对偏移量的理解: 2.结构体的大小计算 2.1结构体中只有普通的数据类型的大小计算 2.2 结构体中有嵌套的结构体的大小计算 3.修改默认对齐数 4.为什么存在内存对齐? 这篇文章主要介绍结构体内存对齐和如何计算大小。 在学习结构体内存…...

【Redis】Redis中的布隆过滤器
【Redis】Redis中的布隆过滤器 前言 在实际开发中,会遇到很多要判断一个元素是否在某个集合中的业务场景,类似于垃圾邮件的识别,恶意IP地址的访问,缓存穿透等情况。类似于缓存穿透这种情况,有许多的解决方法…...

接口测试 —— Jmeter 参数加密实现
Jmeter有两种方法可以实现算法加密 1、使用__digest自带函数 参数说明: Digest algorithm:算法摘要,可输入值:MD2、MD5、SHA-1、SHA-224、SHA-256、SHA-384、SHA-512 String to be hashed:要加密的数据 Salt to be…...

Linux c语言字节序
文章目录 一、简介二、大小端判断2.1 联合体2.2 指针2.3 网络字节序 一、简介 字节序(Byte Order)指的是在存储和表示多字节数据类型(如整数和浮点数)时,字节的排列顺序。常见的字节序有大端字节序(Big En…...

批量将excel中第5列中内容将人名和电话号码进行分列
使用Python可以使用openpyxl库来实现批量将Excel中第5列的内容分列为人名和电话号码的操作。下面是示例代码: import openpyxl def split_names_and_phone_numbers(file_path, sheet_name): # 加载Excel文件 workbook openpyxl.load_workbook(file_path) …...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
