当前位置： 首页 > news >正文

差值结构的复合底部

news 2025/11/3 0:56:11

( A, B )---3*30*2---( 1, 0 )( 0, 1 )

让网络的输入只有3个节点，AB训练集各由6张二值化的图片组成，让A 中有3个点，B中有1个点，且不重合，统计迭代次数并排序。

其中有20组数据

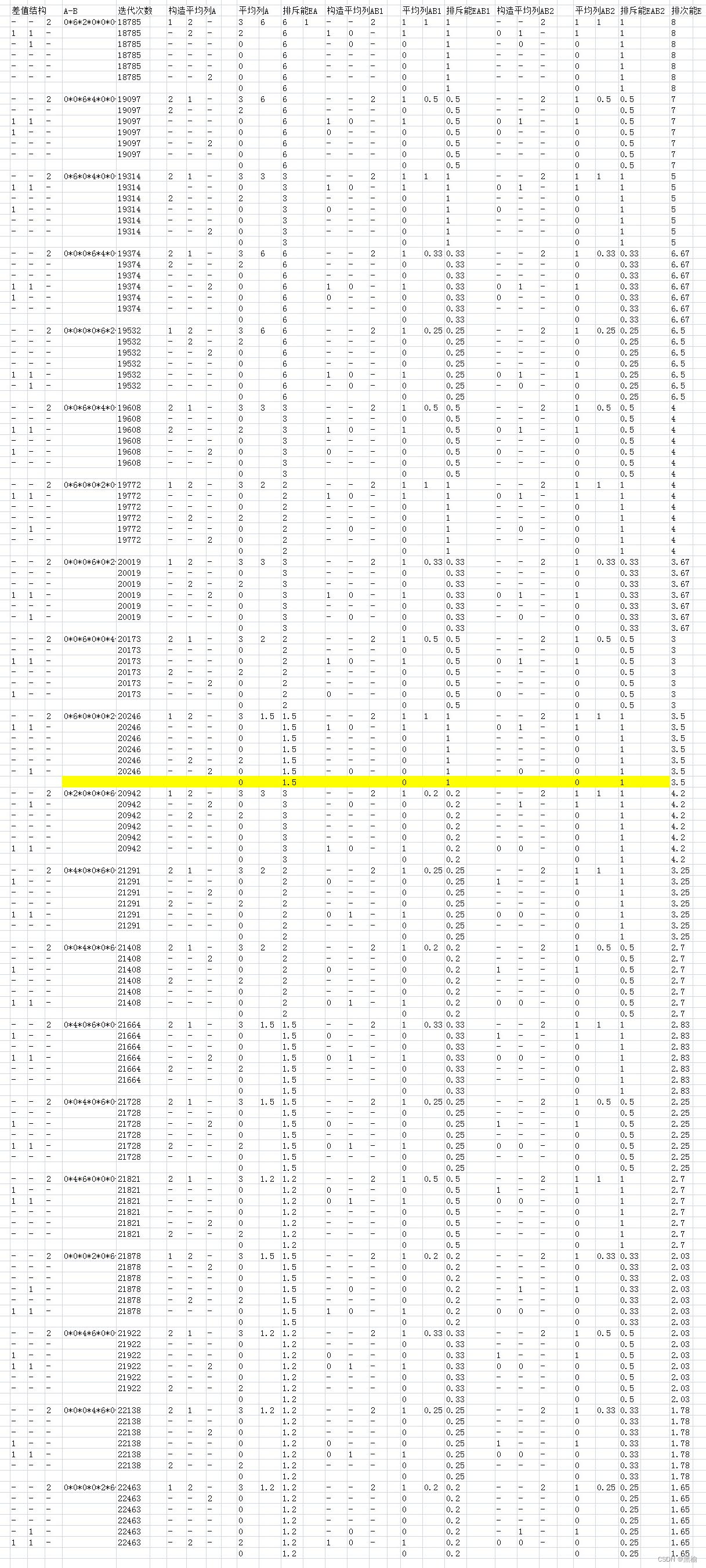
让迭代次数与排斥能成反比，排斥能E=EA+EB+EAB。其中因为B只有1个点,则EB=0.

计算EA相当于假设B中全是0.则结构A的底部就仅仅取决于A的内在特点，与B无关。因此在计算0*2*0*0*0*6-1*0*0*0*0*0的EA是应该调整A的结构

-

-

-

1

1

-

-

1

-

-

-

-

-

-

-

→

-

1

-

-

-

-

-

-

-

-

-

-

-

-

-

1

1

-

-

-

-

1.5

3

因为点最多的行就是结构的天然底部，因此结构0*2*0*0*0*6-1*0*0*0*0*0的EA是3而不是1.5.

而在计算相互作用能的时候，因为训练集AB进样有先后顺序，因此相互作用能的底部由进样先后顺序唯一的确定，

EAB1

EAB2

-

-

2

-

-

2

-

-

2

-

1

-

-

0

-

-

1

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

1

1

-

1

0

-

0

0

-

因此结构0*2*0*0*0*6-1*0*0*0*0*0相互作用能的底部就是- - 2，因为B的点先进样训练，并且假设这种短程相互作用不能隔行传播，且这种短程相互作用只能在AB之间进行，因此相互作用能分成EAB1和EAB2两个独立的结构。

将所有数据汇总

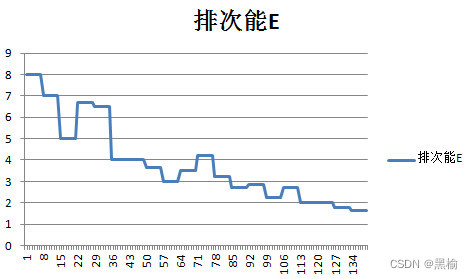
排斥能和迭代次数成反比。因此这个二分类的差值结构对应两种不同的相互作用有两种不同的底部。

相关文章：

差值结构的复合底部

( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 让网络的输入只有3个节点，AB训练集各由6张二值化的图片组成，让A 中有3个点，B中有1个点，且不重合，统计迭代次数并排序。 其中有20组数据 让迭代次数与排斥能成反比，排…...

编程日记 2023/8/21 0:01:48

在Docker 上使用 Nginx 配置https及wss

预先创建挂载文件 /mydata/nginx/conf/nginx.conf /mydata/nginx/cert /mydata/nginx/conf.d /mydata/nginx/html /mydata/nginx/logs运行并且挂载容器 docker run -p 80:80 -p 443:443 --name nginx01 --restartalways \ -v /mydata/nginx/conf/nginx.conf:/etc/nginx/ngi…...

编程日记 2023/8/21 0:00:47

git回退操作

1. 在工作区回退： 此时文件没有经过任何提交 git checkout -- filename2. git add之后回退 git reset HEAD3. git commit 之后回退 git reset --hard commit_id(前4位)其中，commit_id可通过git log查看，例如： qzcryqz MINGW6…...

编程日记 2023/8/20 23:59:46

C++系列-类和对象-静态成员

类和对象-静态成员 静态成员静态成员变量静态成员函数 静态成员 静态成员就是在成员变量或者是成员函数前面加上static关键字。 静态成员变量 所有对象共享同一份数据在编译阶段分配内存类内声明，类外初始化可以通过对象或者类名进行访问。静态成员变量也具有访问…...

编程日记 2023/8/20 23:58:44

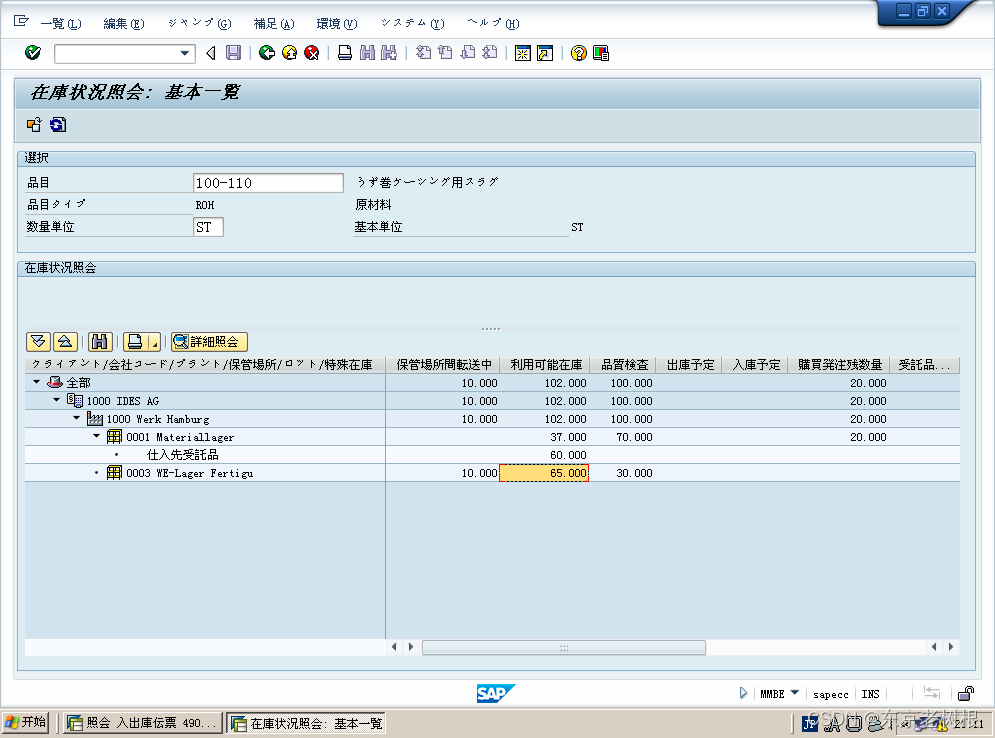
SAP MM学习笔记26- SAP中 振替转记（转移过账）和 在库转送（库存转储）2- 品目Code振替转记 和 在库转送

SAP 中在库移动 不仅有入库（GR），出库（GI），也可以是单纯内部的转记或转送。 1，振替转记（转移过账） 2，在库转送（库存转储） 1&#xff…...

编程日记 2023/8/20 23:57:40

【Python机器学习】实验13 基于神经网络的回归-分类实验

文章目录 神经网络例1 基于神经网络的回归(简单例子)1.1 导入包1.2 构造数据集（随机构造的）1.3 构造训练集和测试集1.4 构建神经网络模型1.5 采用训练数据来训练神经网络模型 实验：基于神经网络的分类(鸢尾花数据集)1. 导入包2. 构造数据集3.…...

编程日记 2023/8/20 23:56:39

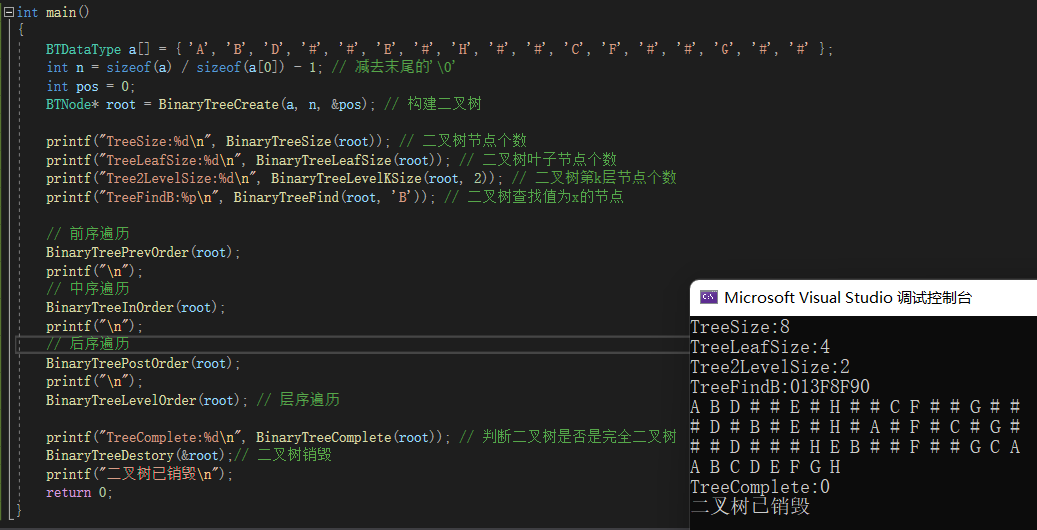
【数据结构】二叉树的链式结构的实现 -- 详解

一、前置说明 在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习。 typedef char BTDataType;typedef struct Binar…...

编程日记 2023/8/20 23:55:38

【C语言】什么是结构体内存对齐？结构体的大小怎么计算？

目录 1.结构体内存对齐 对偏移量的理解：​ 2.结构体的大小计算 2.1结构体中只有普通的数据类型的大小计算 2.2 结构体中有嵌套的结构体的大小计算 3.修改默认对齐数 4.为什么存在内存对齐? 这篇文章主要介绍结构体内存对齐和如何计算大小。 在学习结构体内存…...

编程日记 2023/8/20 23:54:37

【Redis】Redis中的布隆过滤器

【Redis】Redis中的布隆过滤器 前言 在实际开发中，会遇到很多要判断一个元素是否在某个集合中的业务场景，类似于垃圾邮件的识别，恶意IP地址的访问，缓存穿透等情况。类似于缓存穿透这种情况，有许多的解决方法&#xf…...

编程日记 2023/8/20 23:53:34

接口测试 —— Jmeter 参数加密实现

Jmeter有两种方法可以实现算法加密 1、使用__digest自带函数 参数说明： Digest algorithm：算法摘要，可输入值：MD2、MD5、SHA-1、SHA-224、SHA-256、SHA-384、SHA-512 String to be hashed：要加密的数据 Salt to be…...

编程日记 2023/8/20 23:52:33

Linux c语言字节序

文章目录 一、简介二、大小端判断2.1 联合体2.2 指针2.3 网络字节序 一、简介 字节序（Byte Order）指的是在存储和表示多字节数据类型（如整数和浮点数）时，字节的排列顺序。常见的字节序有大端字节序（Big En…...

编程日记 2023/8/20 23:51:30

批量将excel中第5列中内容将人名和电话号码进行分列

使用Python可以使用openpyxl库来实现批量将Excel中第5列的内容分列为人名和电话号码的操作。下面是示例代码： import openpyxl def split_names_and_phone_numbers(file_path, sheet_name): # 加载Excel文件 workbook openpyxl.load_workbook(file_path) …...

编程日记 2023/8/20 23:50:29

WPF DataGrid columns表头根据数据集动态动态生成Demo

思路是这样的&#xff0c;数组集合装表头的信息&#xff0c;遍历这个集合&#xff0c;遍历过程中处理一下数据&#xff0c;然后就把每表头信息添加到dataGrid2.Columns.Add(templateColumn); 1&#xff0c;页面Xaml代码&#xff1a; <DataGrid x:Name"dataGrid" …...

编程日记 2023/8/20 23:49:27

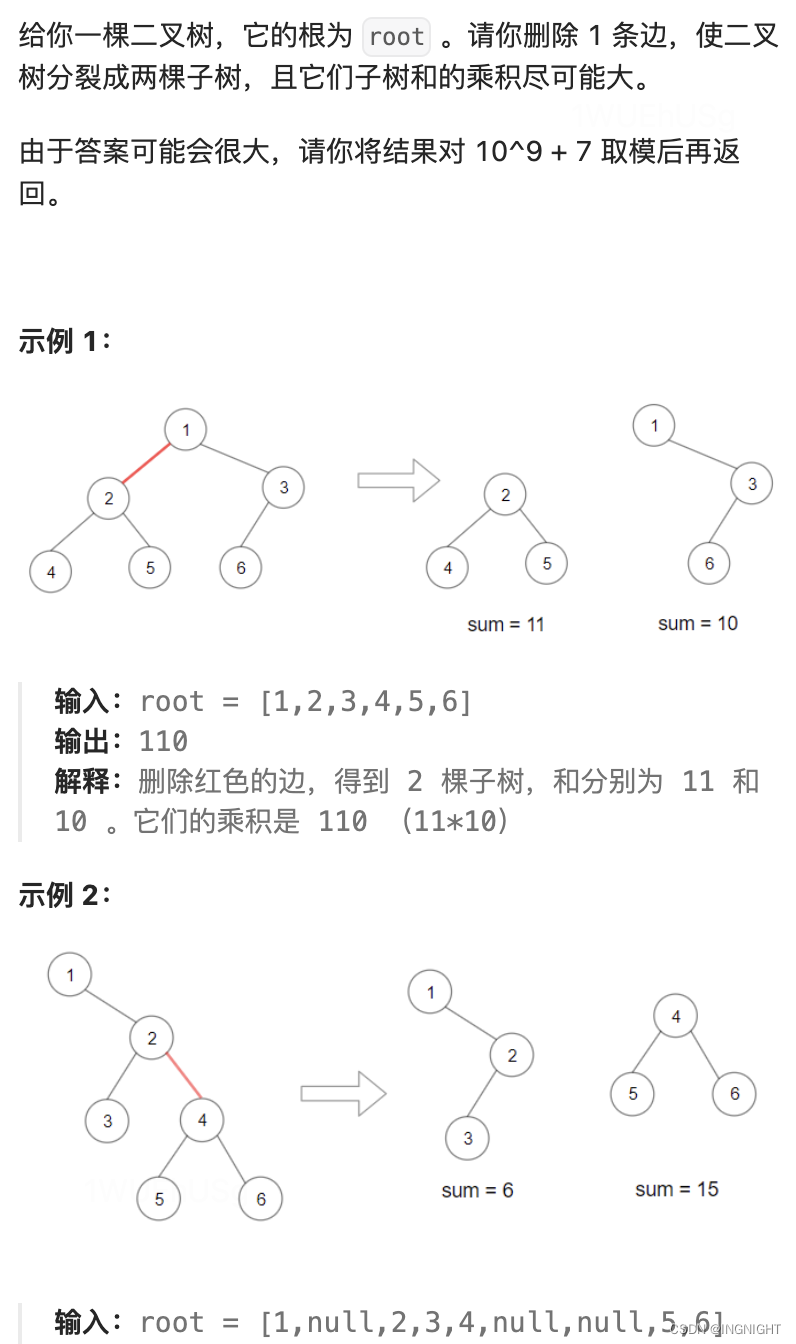
1339. 分裂二叉树的最大乘积

链接&#xff1a; ​​​​​​1339. 分裂二叉树的最大乘积 题解&#xff1a; /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* …...

编程日记 2023/8/20 23:48:25

【C++】Stack和Queue

欢迎来到Cefler的博客&#x1f601; &#x1f54c;博客主页&#xff1a;那个传说中的man的主页 &#x1f3e0;个人专栏&#xff1a;题目解析 &#x1f30e;推荐文章&#xff1a;题目大解析3 目录 &#x1f449;&#x1f3fb;Stack Constructor&#x1f449;&#x1f3fb;Stack …...

编程日记 2023/8/20 23:47:24

Maven之tomcat7-maven-plugin 版本低的问题

tomcat7-maven-plugin 版本『低』的问题 相较于当前最新版的 tomcat 10 而言&#xff0c;tomcat7-maven-plugin 确实看起来很显老旧。但是&#xff0c;这个问题并不是问题&#xff0c;至少不是大问题。 原因 1&#xff1a;tomcat7-maven-plugin 仅用于我们&#xff08;程序员&…...

编程日记 2023/8/20 23:46:22

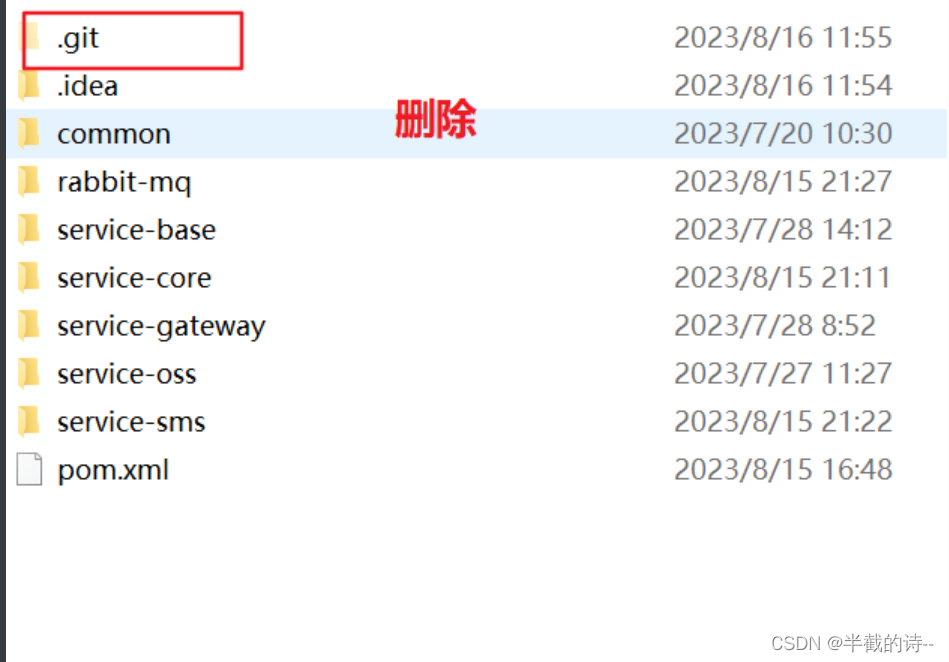
在项目中如何解除idea和Git的绑定

在项目中如何解除idea和Git的绑定 1、点击File--->Settings...(CtrlAltS)--->Version Control--->Directory Mappings--->点击取消Git的注册根路径&#xff1a; 2、回到idea界面就没有Git了&#xff1a; 3、给这个项目初始化 这样就可以重新绑定远程仓库了&#x…...

编程日记 2023/8/20 23:45:20

AGI 在网易云信的技术提效和业务创新

We believe our research will eventually lead to artificial general intelligence, a system that can solve human-level problems. Building safe and beneficial AGI is our mission. ---- OpenAI 通用人工智能 AGI 作为 AI 的终极形态&#xff0c;是 AI 行业内追求的演…...

编程日记 2023/8/20 23:44:18

线性代数的学习和整理9（草稿-----未完成）

3.3 特征值和特征向量是什么&#xff1f; 直接说现在&#xff1a;特征向量这个块往哪个方向进行了拉伸&#xff0c;各个方向拉伸了几倍。这也让人很容易理解为什么&#xff0c;行列式的值就是特征值的乘积。 特征向量也代表了一些良好的性质&#xff0c;即这些线在线性变换后…...

编程日记 2023/8/20 23:43:17

React的useReducer与Reudx对比

useReducer 和 Redux 都是用于处理应用程序的状态管理的工具&#xff0c;但它们在概念和使用场景上存在一些区别。 useReducer&#xff1a; useReducer 是 React 提供的一个 Hook&#xff0c;用于管理局部状态。它接受一个 reducer 函数和初始状态&#xff0c;并返回一个包含当…...

编程日记 2023/8/20 23:42:16

脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）

一、数据处理与分析实战 &#xff08;一&#xff09;实时滤波与参数调整 基础滤波操作 60Hz 工频滤波&#xff1a;勾选界面右侧 “60Hz” 复选框&#xff0c;可有效抑制电网干扰&#xff08;适用于北美地区&#xff0c;欧洲用户可调整为 50Hz&#xff09;。 平滑处理&…...

编程新知 2025/7/31 5:34:43

[10-3]软件I2C读写MPU6050 江协科技学习笔记（16个知识点）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

编程新知 2025/10/27 13:41:27

新能源汽车智慧充电桩管理方案：新能源充电桩散热问题及消防安全监管方案

随着新能源汽车的快速普及&#xff0c;充电桩作为核心配套设施&#xff0c;其安全性与可靠性备受关注。然而&#xff0c;在高温、高负荷运行环境下&#xff0c;充电桩的散热问题与消防安全隐患日益凸显&#xff0c;成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

编程新知 2025/10/31 15:57:04

HBuilderX安装（uni-app和小程序开发）

下载HBuilderX 访问官方网站&#xff1a;https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本&#xff1a; Windows版&#xff08;推荐下载标准版&#xff09; Windows系统安装步骤 运行安装程序&#xff1a; 双击下载的.exe安装文件 如果出现安全提示&…...

编程新知 2025/10/26 7:38:50

Python如何给视频添加音频和字幕

在Python中&#xff0c;给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加&#xff0c;包括必要的代码示例和详细解释。 环境准备 在开始之前&#xff0c;需要安装以下Python库&#xff1a;…...

编程新知 2025/9/3 4:12:17

蓝桥杯3498 01串的熵

问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798&#xff0c; 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

编程新知 2025/11/2 3:42:18

C#中的CLR属性、依赖属性与附加属性

CLR属性的主要特征 封装性&#xff1a; 隐藏字段的实现细节 提供对字段的受控访问 访问控制&#xff1a; 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性&#xff1a; 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑&#xff1a; 可以…...

编程新知 2025/10/7 0:47:59

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2025/10/28 10:00:33

uniapp手机号一键登录保姆级教程（包含前端和后端）

目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号&#xff08;第三种&#xff09;后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

编程新知 2025/10/30 5:13:28

免费数学几何作图web平台

光锐软件免费数学工具&#xff0c;maths,数学制图&#xff0c;数学作图&#xff0c;几何作图&#xff0c;几何&#xff0c;AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

编程新知 2025/10/30 7:44:42