Codeforces EDU 151 Div.2
文章目录
- A. Forbidden Integer
- B. Come Together
- C. Strong Password
- D. Rating System
- E. Boxes and Balls
A. Forbidden Integer
Problem - A - Codeforces
给定整数n,从1~k中选择除了x的数,使这些数之和为n,每个数可以选择无限次
爆搜,从k搜索到1,若当前搜索的数之和为n,返回true
#include <iostream>
using namespace std;const int N = 110;
int T, n, x, k;
int idx, p[N];bool dfs(int s, int start)
{if (start == -1) return false;if (s >= n) return s == n;for (int i = start; i >= 1; -- i ){if (i != x){p[idx ++ ] = i;if (dfs(s + i, start)) return true;idx -- ;}}return dfs(s, start - 1);
}int main()
{cin >> T;while ( T -- ){cin >> n >> k >> x;idx = 0;if (dfs(0, k)){puts("YES");cout << idx << endl;for (int i = 0; i < idx; ++ i ) cout << p[i] << ' ';cout << endl;}else puts("NO");}return 0;
}
B. Come Together
Problem - B - Codeforces
给定三个点,A为起点,BC为终点,从起点走到两个终点的最短路中,最长的公共路径长度是多少?
这是个我的错误思路:一开始以为是bfs最短路,想着在bfs的过程中记录路径
但是矩阵中没有障碍物,完全没有必要bfs,直接将起点于终点的横纵坐标之差相加,就是最短距离了
你可以发现,所有最短路中,无论怎么走,横向距离都是起点与终点的横坐标之差,当然纵向距离也是,所以有了以上结论
那么两条最短路的公共路径呢?将横纵方向分开来看,对于横坐标,若两者的终点都在起点的同一方向(都位于左边或左边),此时横向的最短距离等于横向距离离起点近的终点的横向距离,即 m i n ( x b , x c ) min(x_b, x_c) min(xb,xc)。若两者位于起点的左右两边,那么在横向距离上两者没有公共路径。同理,纵向距离也是如此
#include <iostream>
using namespace std;typedef long long LL;
LL T, xa, ya, xb, yb, xc, yc;int main()
{cin >> T;while ( T -- ){int ans = 0;cin >> xa >> ya >> xb >> yb >> xc >> yc;xb -= xa, yb -= ya, xc -= xa, yc -= ya; // 以a为源点if ((xb > 0) == (xc > 0)) ans += min(abs(xb), abs(xc));if ((yb > 0) == (yc > 0)) ans += min(abs(yb), abs(yc));cout << ans + 1 << endl;}return 0;
}
debug:若用xb * xc > 0判断两点是否位于源点的同一方向,相乘会爆int
C. Strong Password
Problem - C - Codeforces
题目只要求输出YES和NO,没有要求输出具体的序列,所以这题不用想得太复杂
比较暴力的解法是枚举所有可能的序列,用爆搜判断该序列是否为s的子序列,只要有一个序列不是s的子序列就输出YES,否则输出NO
考虑暴力如何优化?两个优化方向:枚举所有可能的序列和爆搜判断
枚举所有可能的序列不太好优化
关于爆搜的优化:由于s中只有字符19,可以预处理出第i个字符右边(包括第i个字符),19第一次出现的位置,若没有出现,位置用无穷表示
枚举t串时,t串的每个字符都有一个范围,假设t串的字符在s串中出现的下标为 x x x,若 x x x越大,s串中用来组成t串的字符就越少,出现相同子序列的概率就越低
以上贪心策略用反证法可以证明正确性,因此对于t串的每个字符,根据每个字符的范围以及字符在s串中出现的位置,确定一个下标最大的字符即可
遇到无穷直接输出YES即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 3e5 + 10, M = 15;
char s[N], l[M], r[M];
int last[N][M], T, m;int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cin >> T;while ( T -- ){cin >> s >> m >> l >> r;int len = strlen(s);memset(last[len], 0x3f, sizeof last[len]);for (int i = len - 1; i >= 0; -- i ){memcpy(last[i], last[i + 1], sizeof last[i + 1]);last[i][s[i] - '0'] = i;}int cur = -1; // cur和next为搜索s串的双指针for (int i = 0; i < m && cur != 0x3f3f3f3f; ++ i ){int next = 0;for (int j = l[i] - '0'; j <= r[i] - '0'; ++ j ){next = max(next, last[cur + 1][j]);} cur = next;}cout << (cur == 0x3f3f3f3f ? "YES\n" : "NO\n");}return 0;
}
debug:如果memset(last[len], 0x3f, sizeof last[len])写成memset(last, 0x3f, sizeof last),直接memset整个last数组会TLE的,考虑到预处理的顺序,只要初始化最后一个一维数组即可last[len]
D. Rating System
Problem - D - Codeforces
看着像是求最大子段和,一开始也是这么想的,但是仔细一想却是不对的
参考视频:最小子段和 动态规划【Codeforces EDU 151】_哔哩哔哩_bilibili
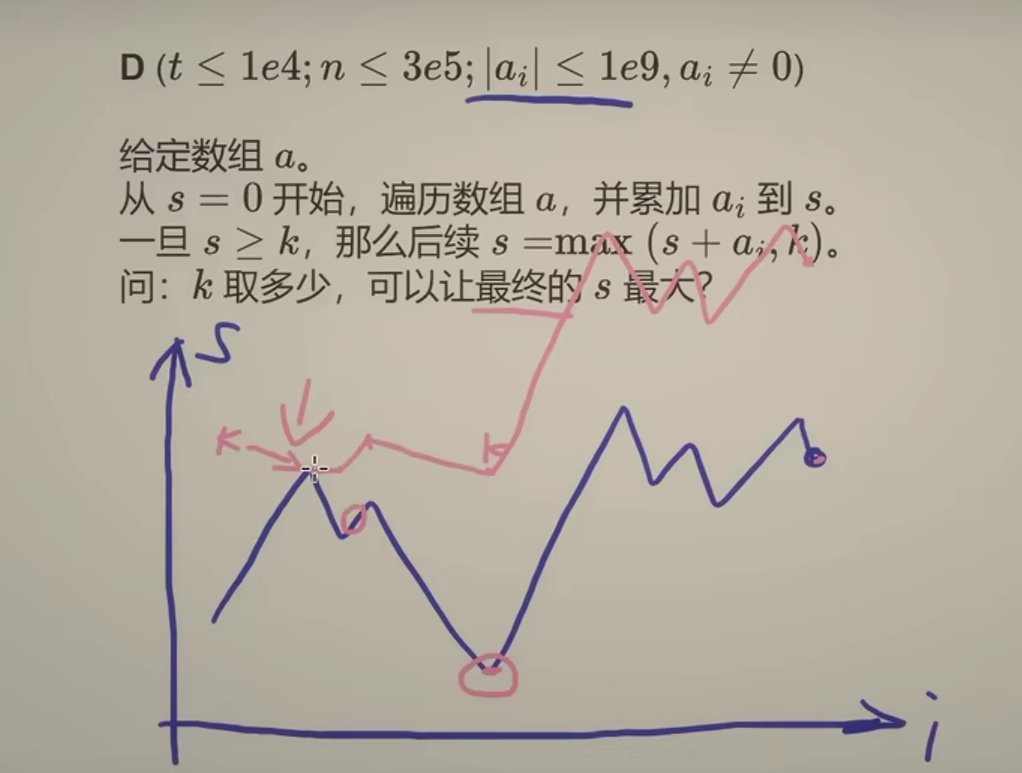
确定一个k值,使分数大于等于k值后不会小于k值,也就是说:抵消分数递达k之后的减分行为
问k为多少,最后的分数最高?显然,抵消的分数越多,最后的分数越高
题目给定每一次分数的变化,即用 a i a_i ai的正负表示分数的加减变化。若要抵消最多的减分,就要找出数组中的最小连续子段和 [ a i , a r ] [a_i, a_r] [ai,ar],再将k设置为 s u m ( a 0 , a i − 1 ) sum(a_0, a_{i-1}) sum(a0,ai−1)
通常求最小子段和,都是使用dp,然而这题求的并不是具体的最小子段和,这题求的是最小子段和的左区间,以及一个前缀和信息。因此只需要在求前缀和的过程中,维护最小子段和的左区间信息即可
#include <iostream>
using namespace std;typedef long long LL;
const int N = 3e5 + 10;
int a[N], T;int main()
{cin >> T;while ( T -- ){int n;cin >> n;for (int i = 0; i < n; ++ i ) cin >> a[i];LL ans = 0, sum = 0, cmax = 0, k;for (int i = 0; i < n; ++ i ){sum += a[i];cmax = max(cmax, sum);LL val = cmax - sum;if (ans < val){ans = val;k = cmax;}}cout << k << endl;}return 0;
}
E. Boxes and Balls
Problem - E - Codeforces
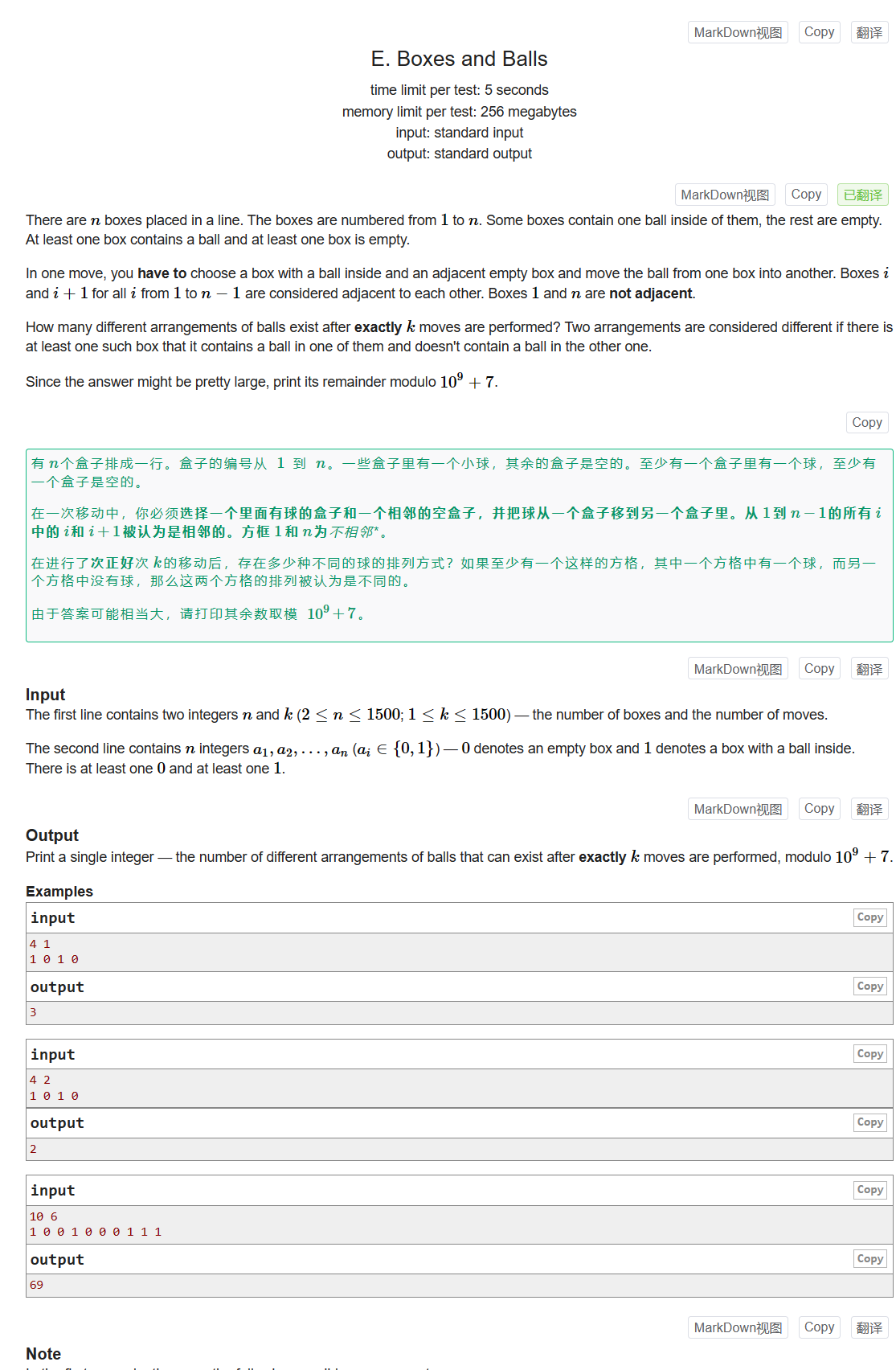
数组中有n个0和1,至少有一个0和1,每次选择一对相邻的0和1进行交换,问经过k次交换后,存在多少种不同的数组?
有些难,以后再来补
相关文章:

Codeforces EDU 151 Div.2
文章目录 A. Forbidden IntegerB. Come TogetherC. Strong PasswordD. Rating SystemE. Boxes and Balls A. Forbidden Integer Problem - A - Codeforces 给定整数n,从1~k中选择除了x的数,使这些数之和为n,每个数可以选择无限次 爆搜&…...
V2board缓存投毒漏洞复现
1.什么是缓存投毒 缓存投毒(Cache poisoning),通常也称为域名系统投毒(domain name system poisoning),或DNS缓存投毒(DNS cache poisoning)。它是利用虚假Internet地址替换掉域名系…...
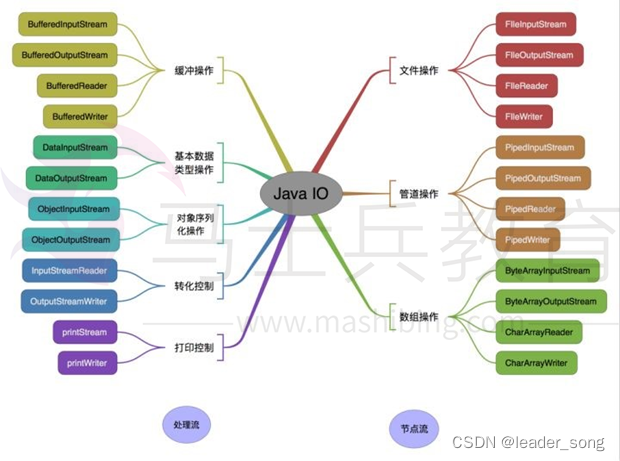
2023面试八股文 ——Java基础知识
Java基础知识 一.Java概述何为编程什么是Javajdk1.5之后的三大版本JVM、JRE和JDK的关系什么是跨平台性?原理是什么Java语言有哪些特点什么是字节码?采用字节码的大好处是什么什么是Java程序的主类?应用程序和小程序的主类有何不同?…...

在linux系统中修改mysql数据目录
目录 1.查看mysql默认存储路径2.停止mysql服务3.移动或复制原数据目录4.修改配置文件5.修改启动文件6.配置AppArmor访问控制规则7.重启apparmor服务8.启动mysql 1.查看mysql默认存储路径 在/etc/mysql/mysql.conf.d/mysqld.cnf中的datadir配置项。 datadir /var/lib/mysql2…...

ORB-SLAM2学习笔记9之图像帧Frame
先占坑,明天再完善… 文章目录 0 引言1 Frame类1.1 成员函数1.2 成员变量 2 Frame类的用途 0 引言 ORB-SLAM2学习笔记8详细了解了图像特征点提取和描述子的生成,本文在此基础上,继续学习ORB-SLAM2中的图像帧,也就是Frame类&#…...
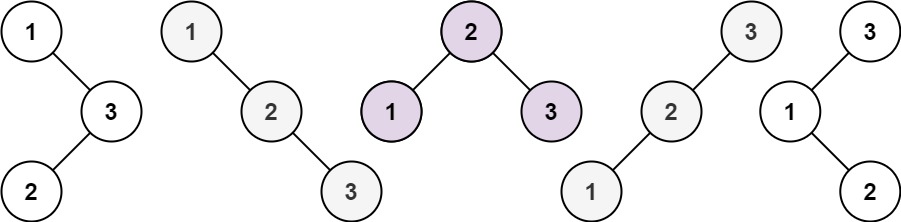
面试热题(不同的二分搜索树)
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 经典的面试题,这部分涉及了组合数学中的卡特兰数,如果对其不清楚的同学可以去看我以前的博客卡特兰数 …...

MybatisPlus整合p6spy组件SQL分析
目录 p6spy java为什么需要 如何使用 其他配置 p6spy p6spy是一个开源项目,通常使用它来跟踪数据库操作,查看程序运行过程中执行的sql语句。 p6spy将应用的数据源给劫持了,应用操作数据库其实在调用p6spy的数据源,p6spy劫持到…...
项目实战 — 博客系统③ {功能实现}
目录 一、编写注册功能 🍅 1、使用ajax构造请求(前端) 🍅 2、统一处理 🎄 统一对象处理 🎄 保底统一返回处理 🎄 统一异常处理 🍅 3、处理请求 二、编写登录功能 🍅 …...
卷积神经网络全解:(AlexNet/VGG/ GoogLeNet/LeNet/ResNet/卷积/激活/池化/全连接)、现代卷积神经网络、经典卷积神经网络
CNN,卷积神经网络,Convolution Neural Network 卷积计算公式:N (W-F2p)/s1 这个公式每次都得看看,不能忘 1 经典网络 按照时间顺序 1.1 LeNet LeNet是 Yann LeCun在1998年提出,用于解决手…...
简述)
WDM 模型(Windows Driver Model)简述
WDM 模型(Windows Driver Model) 是微软公司为 Windows98 和 Windows2000 的驱动程序设计的一种架构,在 WDM 驱动程序模型中,每个硬件设备 至少有两个驱动程序。其中一个为功能驱动程序,它了解硬件工作的所有细节,负 责初始化 …...

【算法刷题之数组篇(1)】
目录 1.leetcode-59. 螺旋矩阵 II(题2.题3相当于二分变形)2.leetcode-33. 搜索旋转排序数组3.leetcode-81. 搜索旋转排序数组 II(与题目2对比理解)(题4和题5都是排序双指针)4.leetcode-15. 三数之和5.leetcode-18. 四数之和6.leet…...

【数据挖掘】使用 Python 分析公共数据【01/10】
一、说明 本文讨论了如何使用 Python 使用 Pandas 库分析官方 COVID-19 病例数据。您将看到如何从实际数据集中收集见解,发现乍一看可能不那么明显的信息。特别是,本文中提供的示例说明了如何获取有关疾病在不同国家/地区传播速度的信息。 二、准备您的…...

html怎么插入视频?视频如何插入页面
html怎么插入视频?视频如何插入页面 HTML 的功能强大,基本所有的静态效果都可以在此轻松呈现,各种视频网站内有大量的视频内容,本篇文章教你如何在 html 中插入视频 代码如下: <!DOCTYPE html> <html> …...
游戏服务端性能测试
导语:近期经历了一系列的性能测试,涵盖了Web服务器和游戏服务器的领域。在这篇文章中,我将会对游戏服务端所做的测试进行详细整理和记录。需要注意的是,本文着重于记录,而并非深入的编程讨论。在这里,我将与…...
【使用Zookeeper当作注册中心】自己定制负载均衡常见策略
自己定制负载均衡常见策略 一、前言随机(Random)策略的实现轮询(Round Robin)策略的实现哈希(Hash)策略 一、前言 大伙肯定知道,在分布式开发中,目前使用较多的注册中心有以下几个&…...
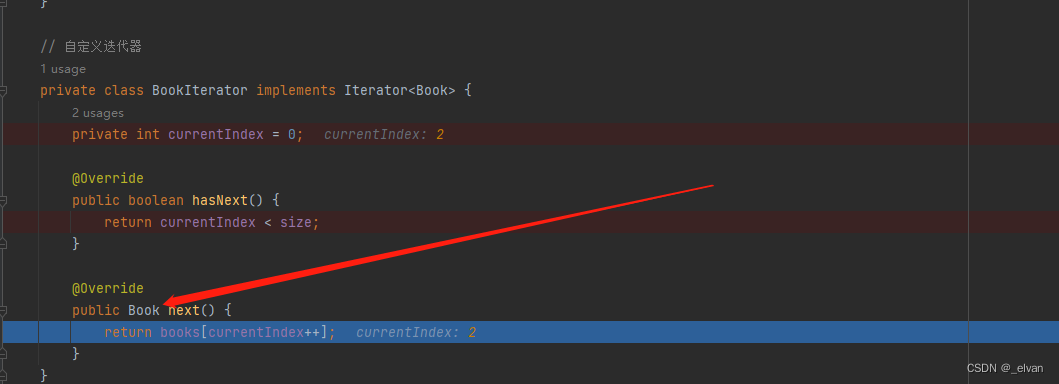
设计模式十七:迭代器模式(Iterator Pattern)
迭代器模式(Iterator Pattern)是一种行为型设计模式,它提供了一种访问聚合对象(例如列表、集合、数组等)中各个元素的方法,而无需暴露其内部表示。迭代器模式将遍历元素和访问元素的责任分离开来࿰…...

Python制作爱心并打包成手机端可执行文件
前言 本文是想要将python代码打包成在手机上能执行的文件 尝试了几个库, 有这也那样的限制,最终还是选了BeeWare 环境:python3.7.x 开始 找到打包有相关工具os-android-apk-builder,buildozer,cx_Freezeÿ…...
以及多容器通信和统一配置)
使用docker-compose.yml快速搭建开发、部署环境(nginx、tomcat、mysql、jar包、各种程序)以及多容器通信和统一配置
目录 docker-compose语法(更多说明可查看下面代码)imagehostnamecontainer_namevolumesnetworks yml文件的使用启动停止 开发环境(这里以python为例)部署环境nginxmysqltomcatjar包打包后的可执行程序 常见问题与解决方案多个容器…...

管理类联考——逻辑——真题篇——按知识分类——汇总篇——二、论证逻辑——支持加强——第三节——分类3——类比题干支持
文章目录 第三节 支持加强-分类3-类比题干支持真题(2017-28)-支持加强-正面支持-表达“确实如此”真题(2017-36)-支持加强-正面支持-表达“确实如此”真题(2017-39)-支持加强-正面支持-方法有效或方法可行,但多半不选择方法无恶果真题(2017-50)-支持加强真题(2018-2…...

搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nums[1], …, …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
