多因子模型(MFM)
多因子模型(Muiti-Factor M: MFM)
- 因子投资基础
- CAPM (资本资产定价模型)
- APT套利定价理论
- 截面数据 & 时间序列数据 & 面板数据
- 定价误差 α\alphaα
- alpha 出现的原因
- 线性多因子模型
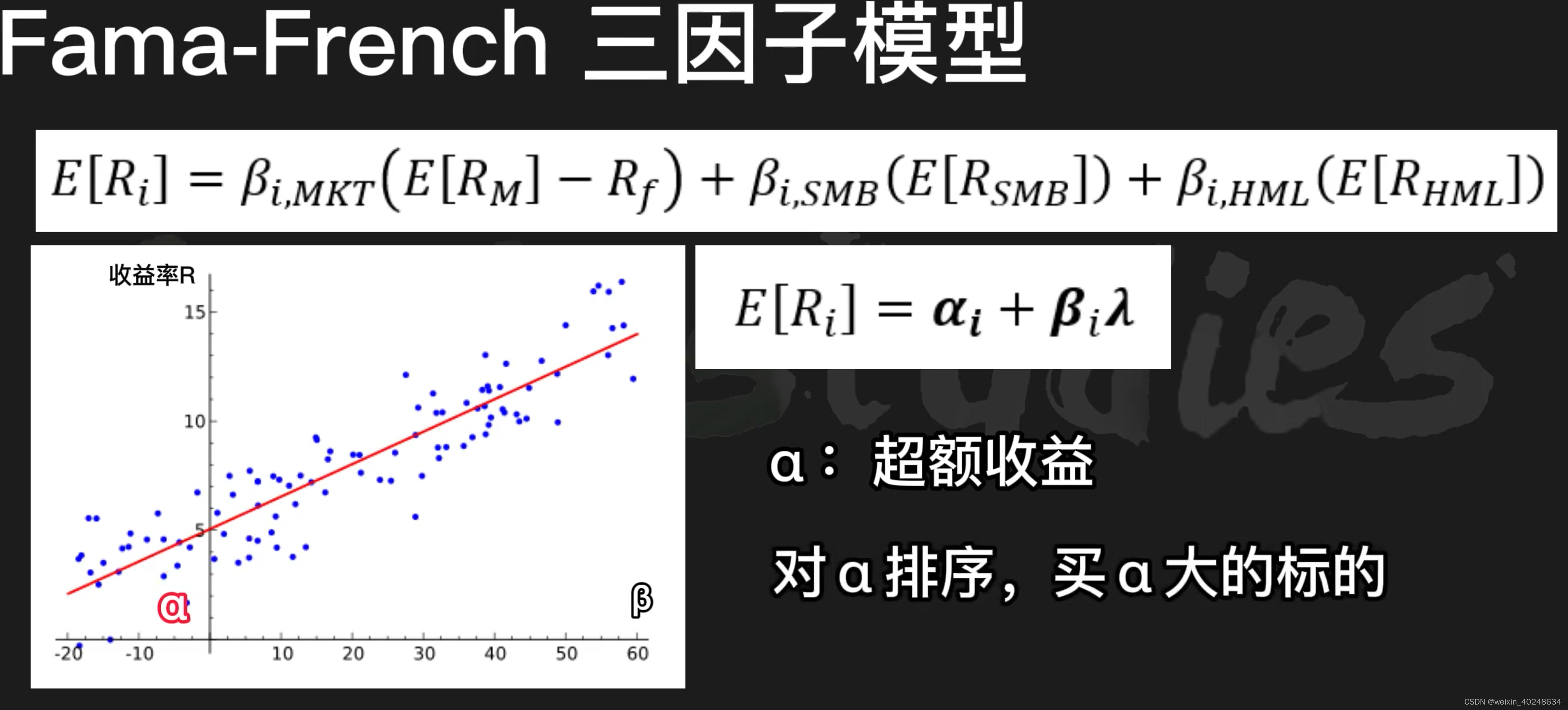
- Fama-French三因子模型
- 三因子的计算公式
- 利用alpha大小进行购买股票
因子投资基础
CAPM (资本资产定价模型)


横轴为风险(标准差sigma),纵轴为预期收益。
风险越高,收益就越高
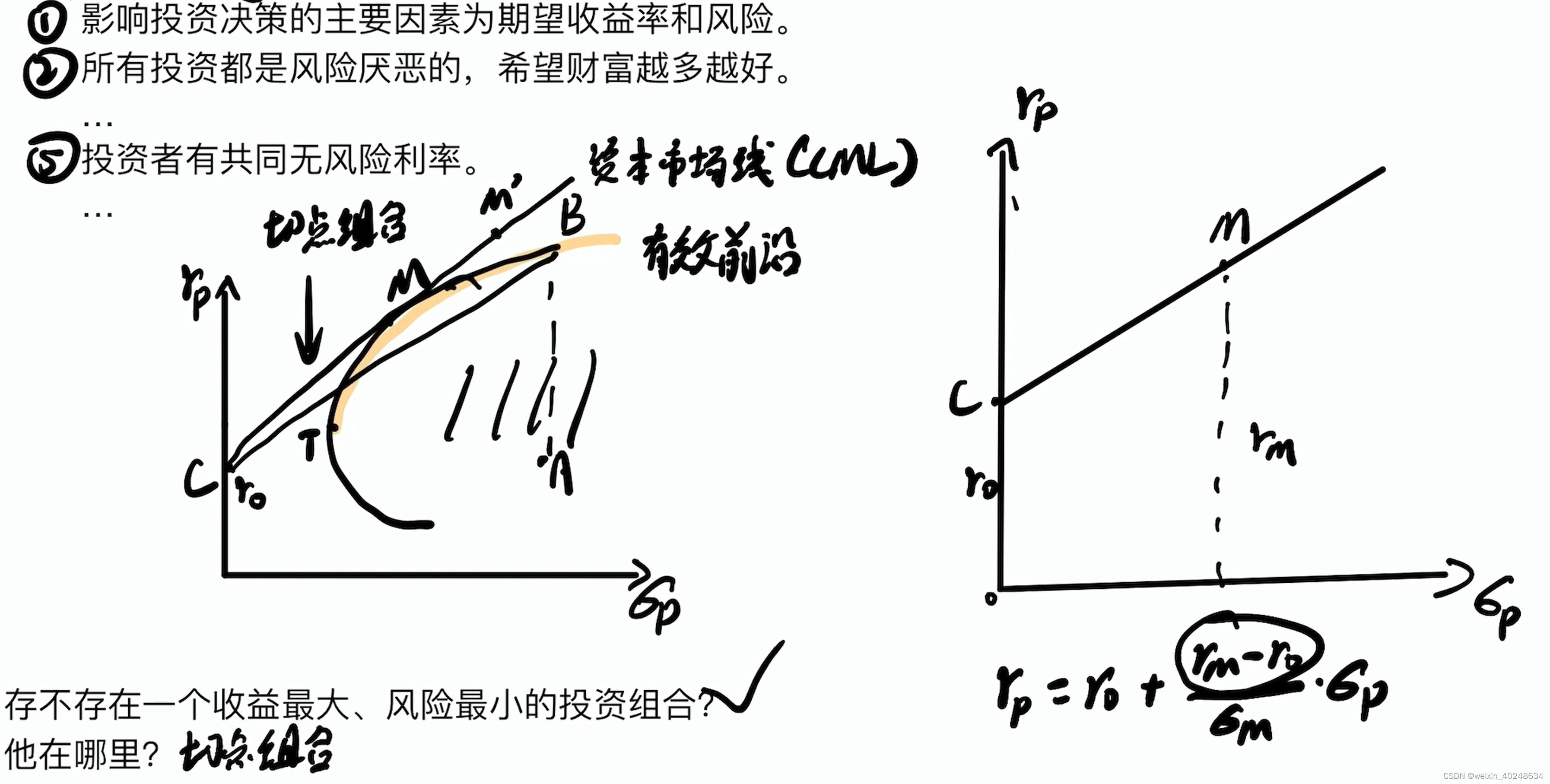
这条C-M直线描绘的对于整个市场的收益,其对于单支股票并不适应,所以后面换了个横轴, 为单个证券对整个市场的联动性σi,MσM\frac{\sigma_{i,M}}{\sigma_M}σMσi,M。
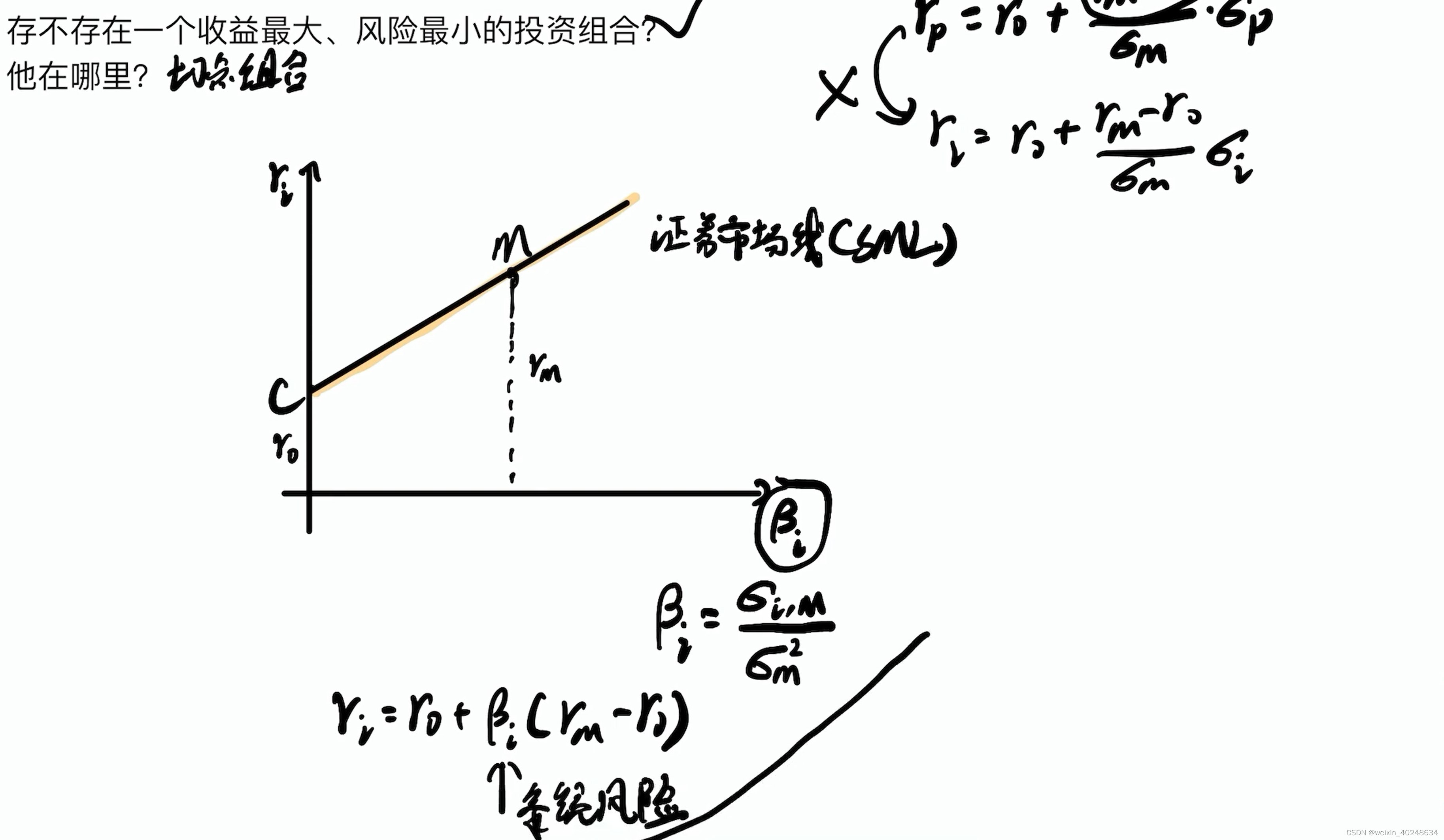
也就是CAPM公式了

E[Ri]=Rf+cov(Ri,RM)var(RM)(E[RM]−R0)cov(RM,RM)var(RM)=Rf+cov(Ri,RM)var(RM)(E[RM]−R0)E[R_i] = R_f +\frac{cov(R_i,R_M)}{var(R_M)} \frac{(E[R_M]-R_0)}{\frac{cov(R_M,R_M)}{var(R_M)}} = R_f +\frac{cov(R_i,R_M)}{var(R_M)}(E[R_M]-R_0) E[Ri]=Rf+var(RM)cov(Ri,RM)var(RM)cov(RM,RM)(E[RM]−R0)=Rf+var(RM)cov(Ri,RM)(E[RM]−R0)
注意这var(R)=σ2(R)var(R)=\sigma^2(R)var(R)=σ2(R)



APT套利定价理论

截面数据 & 时间序列数据 & 面板数据
- 横截面数据,也称截面数据、静态数据,是统计学与计量经济学中的一类数据集,通过观察许多主体(如个人、公司、国家、地区等)在同一时间点或同一时间段截面上反映一个总体的一批(或全部)个体的同一特征变量的观测值。例如,经济普查数据、人口普查数据、家庭收入调查数据。横断面数据分析通常比较被选择的主体的差异。
-时间序列数据,小规模数据或者聚集数据在一系列时间点上被观测。 - 面板数据(或称纵向数据)是截面数据与时间序列数据的结合。面板数据不同于混合横截面数据(pooled cross-sectional data)。面板数据是对 同一主体的不同时间点的观测值。混合横截面数据是在不同时点从同一个大总体内部分别抽样,将所得到的数据混合起来的一种数据集。如许多关于个人、家庭和企业的调查,每隔一段时间,常常是每隔一年,重复进行一次,如果每个时期都抽取一个随机样本,那么把所得到的随机样本合并起来就给出一个混合横截面。
横截面数据可施加横截面回归,及对截面数据的回归分析。
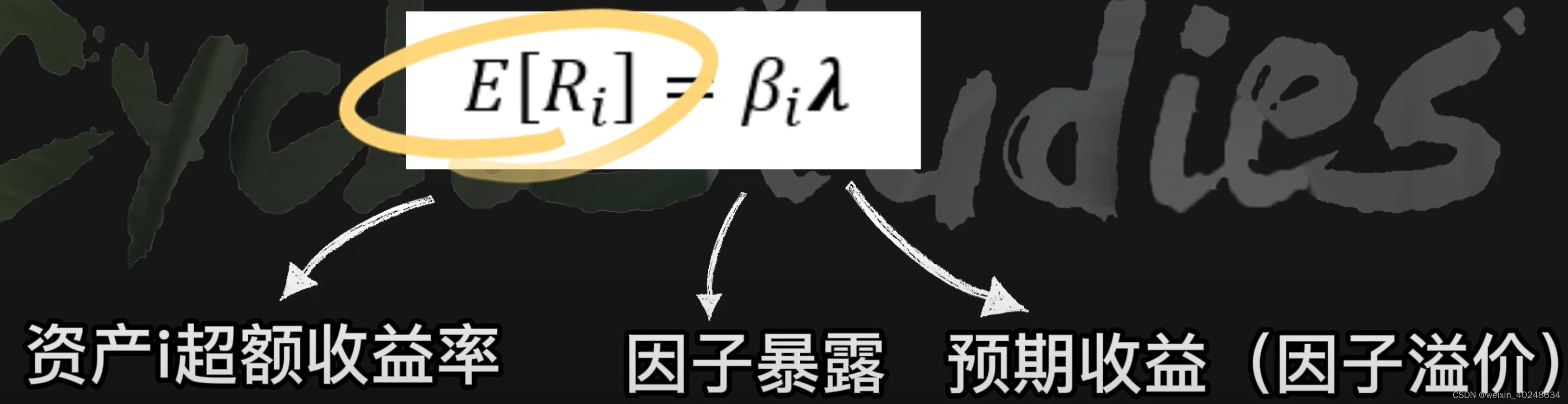
定价误差 α\alphaα

alpha 出现的原因

如果alpha 显著不为0, 那么称之为异象(Anomaly), 从投资的角度来说,我们就需要买入alpha显著不为0, alpha越大的资产

线性多因子模型

这里从单个时间点做分析,T时刻资产i的超额收益率RiTR_{iT}RiT ;αi\alpha_iαi 表示第iii 个资产的定价误差,βi\beta_iβi表示因子暴露矩阵, λT\lambda_TλT表示T时刻的因子收益率, ϵiT\epsilon_{iT}ϵiT 表示T时刻的随机扰动,


Fama-French三因子模型



三因子的计算公式

利用alpha大小进行购买股票
我们最后的目的就是为了得到alpha,使用alpha来判断资产的潜力.
截屏来源: https://www.youtube.com/live/Bf79VTLRjtI
相关文章:

多因子模型(MFM)
多因子模型(Muiti-Factor M: MFM)因子投资基础CAPM (资本资产定价模型)APT套利定价理论截面数据 & 时间序列数据 & 面板数据定价误差 α\alphaαalpha 出现的原因线性多因子模型Fama-French三因子模型三因子的计算公式利用alpha大小进行购买股票…...

django项目实战一(django+bootstrap实现增删改查)
目录 一、创建django项目 二、修改默认配置 三、配置数据库连接 四、创建表结构 五、在app当中创建静态文件 六、页面实战-部门管理 1、实现一个部门列表页面 2、实现新增部门页面 3、实现删除部门 4、实现部门编辑功能 七、模版的继承 1、创建模板layout.html 1&…...
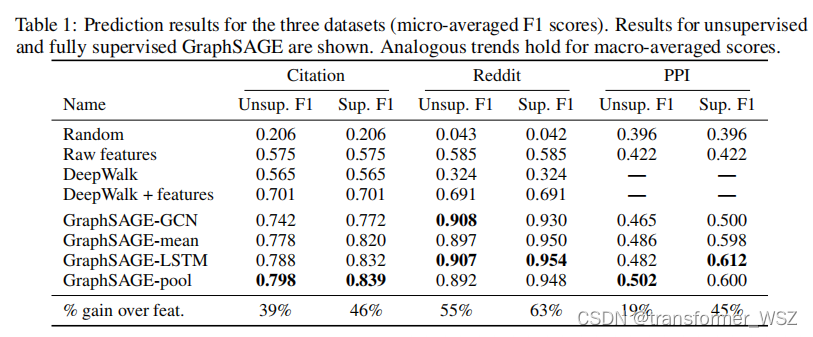
graphsage解读
传统的图方法都是直推式(transductive)的,学习到的是结构固定的图模型,一旦有新的节点加入,便需要重新训练整个图网络,泛化性不强。GraphSAGE是归纳式(inductive)的,它学习一种映射:通过采样和聚合邻居节点…...
一文带你读懂Dockerfile
目录 一、概述 二、DockerFile构建过程解析 (一)Dockerfile内容基础知识 (二)Docker执行Dockerfile的大致流程 (三)总结 三、DockerFile常用保留字指令 四、案例 (一)自定义…...
用python实现对AES加密的视频数据流解密
密码学中的高级加密标准(Advanced Encryption Standard,AES),又称Rijndael加密法。 在做网络爬虫的时候,会遇到经过AES加密的数据,可以使用python来进行解密。 在做爬虫的时候,通常可以找到一个key,这个key是一个十六进制的一串字符,这传字符是解密的关键。所以对于…...

网络高可用方案
目录 1. 网络高可用 2. 高可用方案设计 2.1 方案一 堆叠 ha负载均衡模式 2.2 方案二 OSPF ha负载均衡模式 3. 高可用保障 1. 网络高可用 网络高可用,是指对于网络的核心部分或设备在设计上考虑冗余和备份,减少单点故障对整个网络的影响。其设计应…...

简单的认识 Vue(vue-cli安装、node安装、开发者工具)
Vue1、Vue 与其他框架的对比及特点1.1 Vue.js 是什么1.2 作者1.3 作用1.4 Vue 与其他框架的对比2、安装 Vue 的方法2.1 CDN 引入2.2 脚手架工具2.3 vue 开发者工具安装3、创建第一个实例4、理解 Vue 的 MVVM 模式5、数据双向绑定5.1 感受响应式实验总结1、Vue 与其他框架的对比…...
如何写一个 things3 client
Things3[1] 是一款苹果生态内的任务管理软件,是一家德国公司做的,非常好用。我前后尝试了众多任务管理软件,最终选定 things3,以后有机会会写文章介绍我是如何用 things3 来管理我的日常任务。本文主要介绍欧神写的 tli[2] 工具来…...

人工智能原理复习 | 命题逻辑和谓词演算
文章目录 一、前言二、命题逻辑三、谓词逻辑CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 数理逻辑思想的起源:莱布尼茨之梦。古典数理逻辑主要包括两部分:命题逻辑和谓词逻辑,命题逻辑又是谓词逻辑的一种简单情形。 逻辑研究的基本内容: 语法。语言部分:基…...
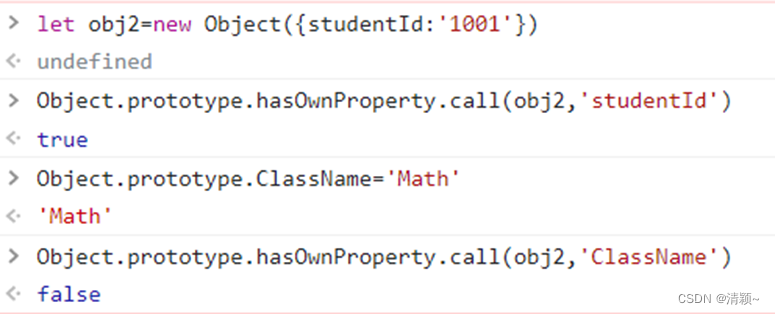
前端基础面试题:如何判断对象是否具有某属性?遍历数组的方法有哪些?
一、如何判断对象具有某属性? 如:let obj{name:zhangsan,age:21} 有以下方法 ( property 为属性名的变量,实际上是key,键名): 1. property in obj 效果如图: in 运算符 2. Reflect.has(obj, property)…...
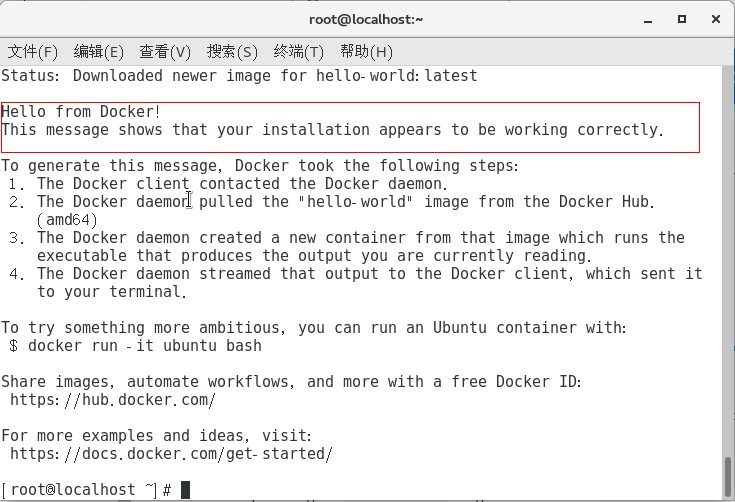
Docker入门和安装教程
一、Docker入门简介 Docker 是一个基于GO语言开发的开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux机器上,也可以实现虚拟化。 容器是完全使用沙箱机制,相互之间不会…...
有了java基础,迅速学完Python并做了一份笔记-全套Python,建议收藏
面向过程Python简介Python和Java的解释方式对比Java:源代码 -> 编译成class -> Jvm解释运行Python:源代码 -> Python解释器解释运行我经常和身边的Java开发者开玩笑说:“Java真变态,别的语言都是要么直接编译要么直接解释…...
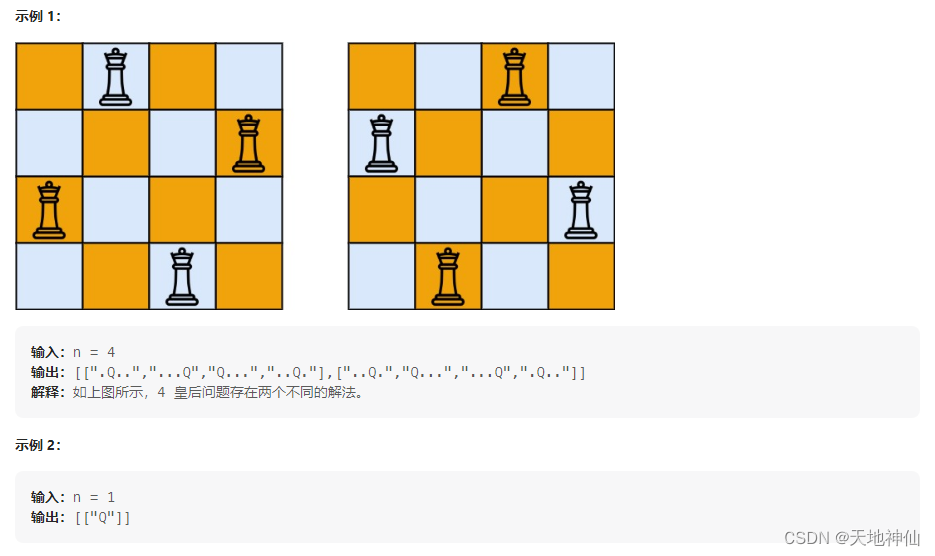
LeetCode——51. N 皇后
一、题目 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案…...

jQuery基本操作
学习目标: 会使用基本选择器获取元素 会使用层次选择器获取元素 会使用属性选择器获取元素 会使用过滤选择器获取元素 学习内容: 1.回顾jQuery语法结构 语法 $(selector).action; 工厂函数$():将DOM对象转化为jQuery对象。 选择器 sele…...
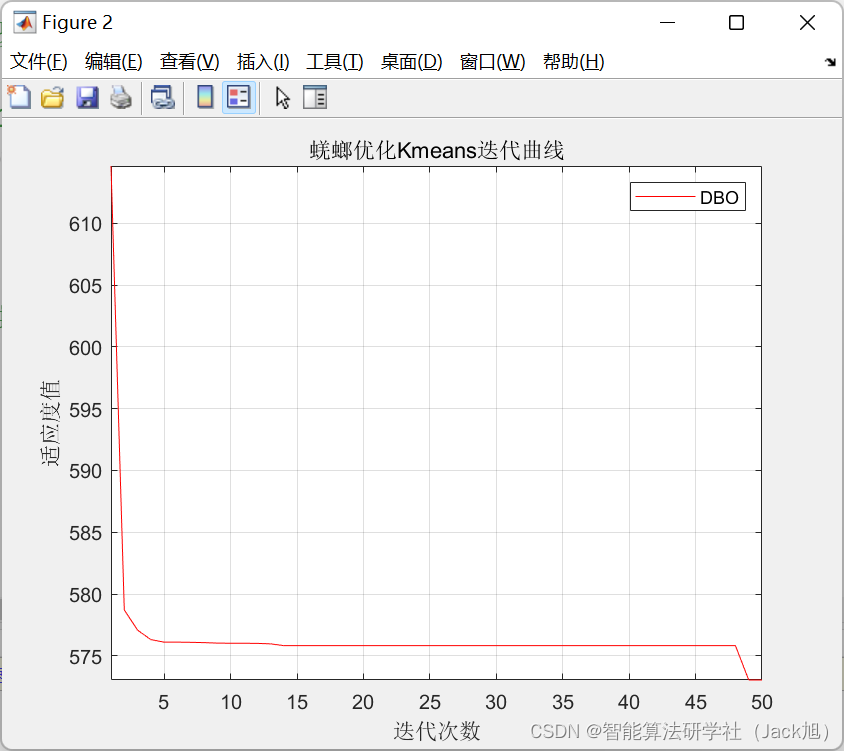
基于蜣螂算法优化Kmeans图像分割-附代码
基于蜣螂优化Kmeans图像分割算法 - 附代码 文章目录基于蜣螂优化Kmeans图像分割算法 - 附代码1.Kmeans原理2.基于蜣螂算法的Kmeans聚类3.算法实验结果4.Matlab代码摘要:基于蜣螂优化Kmeans图像分割算法。1.Kmeans原理 K-Means算法是一种无监督分类算法,…...
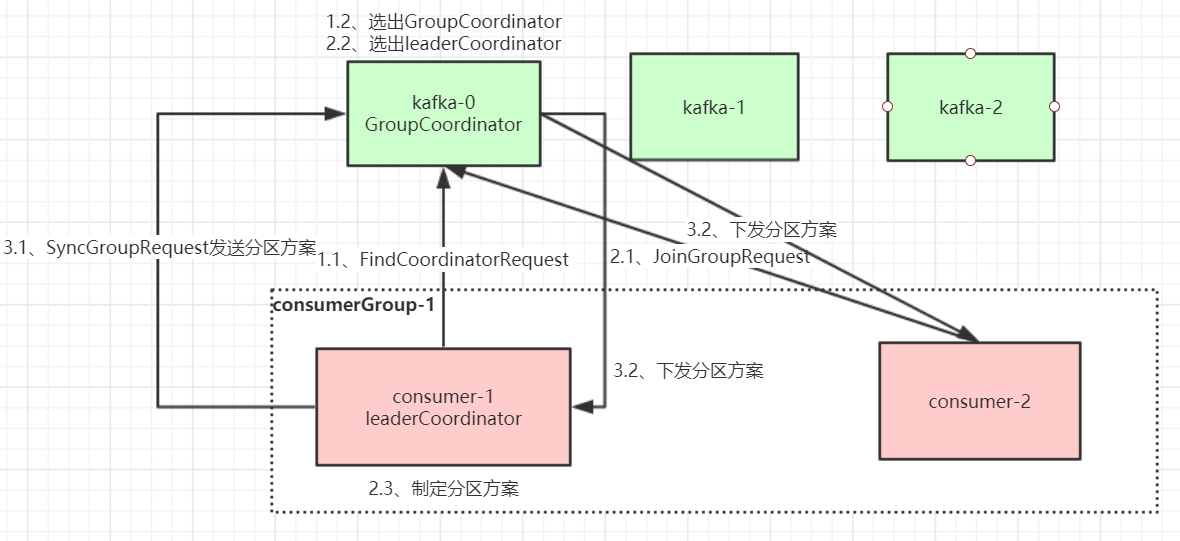
第二章 Kafka设计原理详解
第二章 Kafka设计原理详解 1、Kafka核心总控制器Controller 在 Kafka 集群中会有一个或者多个 broker,其中有一个 broker 会被选举为控制器(Kafka Controller),它负责管理整个集群中所有分区和副本的状态。 当某个分区的 leader…...

《NFL橄榄球》:费城老鹰·橄榄1号位
费城老鹰(英语:Philadelphia Eagles)是美国橄榄球联盟在宾夕法尼亚州费城的一支球队。1933年在国家橄榄球联盟扩编时与匹兹堡钢人和辛辛那提红人一起加入;1943年赛季因二次大战的缘故,和匹兹堡钢人作短暂的合并。 在20…...
【人工智能AI】四、NoSQL进阶《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章的标题是《四、NoSQL进阶》,不少于3000字。帮我细化到三级目录,使用markdown格式。这篇文章的目录是: 四、NoSQL 进阶 4.1 NoSQL 高可用 4.2 NoSQL 数据安全 4.3 NoSQL 性能优化 4.4 总结 四、…...
K8S 部署 Jenkins
本文使用 bitnami 镜像部署 Jenkins 官方文档:https://github.com/bitnami/charts/tree/main/bitnami/jenkins 添加 bitnami 仓库 helm repo add bitnami https://charts.bitnami.com/bitnami自定义 values.yaml storageClass:集群的存储类ÿ…...

【人工智能AI】五、NoSQL 应用实践《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章的标题是《五、NoSQL 应用实践》,不少于3000字。目录需要细化到三级目录,使用markdown格式。这篇文章的大的目录是: 五、NoSQL 应用实践 5.1 NoSQL 实时数据分析 5.2 NoSQL 分布式系统 5.3 NoS…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
